논문: https://arxiv.org/abs/2106.13228
프로젝트 홈페이지 : https://hypernerf.github.io/
Github: https://github.com/google/hypernerf

Motivation

• Deformation 기반의 방법들은 연속적인 deformation field를 요구하므로 deformation field에서 불연속적인 topological change들을 모델링하는 데에 어려움을 겪었다.

Contributions

• 우리는 NeRF를 더 높은 차원의 공간으로 올림으로써 이 한계를 다뤘고 각 입력 이미지에 대응하는 5D radiance field를 이 "hyper space"를 통한 slice로 표현했다.
• Ambient slicing surface에서의 좌표를 추가적 input으로 넣어줌으로써 deformation 뿐만 아니라 topological variation들도 잘 모델링할 수 있게 됨.

Future direction

• Topological changes 외에도 추가적으로 보완할 수 있는 내용들 생각

Abstract

Fig. 1. Neural Radiance Fields는 deformation을 다룰 수 있는 능력이 주어졌을 때, 동적인 human subject들을 포착할 수 있고 현저한 deformation이나 topological variation이 있을 때 자주 어려움을 겪는다. (d)에서 보듯이 고차원의 공간에서 shape들이 family를 모델링할 때, HyprNeRF 모델은 topological variation을 다룰 수 있고 더 현실적인 rendering과 더 정확한 geometric reconstruction을 생성한다.

• NeRF는 전례없는 정확도로 scene을 reconstruct하고 다양한 최신 연구들이 NeRF가 dynamic scene들을 다루도록 확장해왔다.
• 그러나 deformation 기반의 방법들은 연속적인 deformation field를 요구하기에 deformation field에서 불연속적인 topological change들을 모델링하는 데에 어려움을 겪었다.
• 우리는 NeRF를 더 높은 차원의 공간으로 올림으로써 이 한계를 다뤘는데 각 입력 이미지에 대응하는 5D radiance field를 이 "hyper space"를 통한 slice로 표현했다.
• 우리는 우리의 방법을 2가지 task들에 대해 평가했다.
  • 시각적 plausibility를 유지하면서 "Moments" 들 사이에 interpolate하는 것
  • 고정된 순간에서의 novel view synthesis
• 우리는 HyperNeRF라고 불리는 우리의 방법이 2가지 task들에 대해 존재하는 방법들을 압도함을 보였다.
  • Nerfies와 비교할 때, HyperNeRF는 interpolation을 통해 평균적 error를 4.1% 줄이고 측정된 LPIPS를 novel view synthesis에 대해 8.6% 줄인다.

1. Introduction

• Topological change들은 motion 불연속성이나 singularities를 야기하므로 움직이는 3차원 scene들을 재구성하는 알고리즘에 문제를 야기한다.
• Topology를 다루는 현명한 접근법은 3D scene을 4D volume에서의 level set으로서 표현하는 것이다.
• 고차원의 주변 공간에서 정적인 물체들의 움직이는 scene들을 모델링하는 level set 방법들과 smooth 또는 불연속적 transformations로서의 topological change들이 탐구되어 왔다.
• 본 논문에서, 우리는 deformable neural radiance fields의 level set framework를 도입했고 topology에서 변화를 겪고 있는 object들의 photorealistic free-viewpoint rendering을 생성한다.
• 우리는 MLP와 같은 전통적인 level set framework를 사용해 일반화한다.
  • Classical level set들이 single 주변 차원들을 더하므로 우리는 더 자유도를 주기 위해 주변 차원의 어떤 수든 더할 수 있다.
  • Level set들을 hyperplane으로 제한하기 보다, 우리는 MLP를 통해 표현된 일반적이고 curved slicing manifolds를 허용한다.
• 우리의 접근법은 hyperdimensional NeRF - a HyperNeRF를 통해 nonplanar slice로서 각 관측 frame을 모델링한다.
• 더 높은 차원의 입력들을 사용하는 이전의 방법들은 상당한 regularization이나 추가적인 supervision을 요구한다. 이와 대조적으로, 우리는 관측들의 정보를 결합하는데 강한 성능을 보인 deformaiton field를 유지하고 regularizer 대신에 최적화 전략을 사용하여 더 높은 차원에서 smooth behavior를 장려했다.
• 이는 우리의 방법이 몇몇 포즈가 작은 각도로부터만 관측되는 경우에도 high-quality의 geometry를 재구성할 수 있게 해준다.
• 우리의 방법은 사용자들이 monocular video로부터 넓은 범위의 도전적인 deforming scene들의 photorealistic free-viewpoint reconstruction를 포착할 수 있게 한다.
• 우리는 우리의 방법들을 2가지 task들에 대해 평가했다.
  • Visual plausibility를 유지하며 "moments" 사이를 smooth하게 interpolate하는 것
  • 고정된 moments들과 함께 novel view synthesis
• 우리의 방법은 2가지 task들에 대해 더 적은 artifact들과 함께 더 날카롭고, 높은 quality의 결과를 생성한다.

2. Related work

2.1. Non-rigid reconstruction

• Non-rigid reconstruction 기법들의 common approach는 scene을 scene geometry의 canonical model과 각 입력 이미지를 재현하기 위해 canonical scene geometry를 warp하는 a deformation model로 분해하는 것이다.
• Monocular video stream만 사용하는 것은 편하고 비용이 적게 들지만 factorization이나 regularization에 의해 개선되어야 하는 현저한 모호성을 도입한다.
• 다수의 카메라나 depth sensor들을 이용하는 것은 문제를 과도하게 제한한다.
• 머신러닝 기법들은 효율적으로 depth sensor에 적용되었을 때, non-rigid reconstruction에 쓰였다.
• 우리의 방법은 depth sensor들이나 multi-view capture system들을 요구하지 않고 전통적인 스마트폰 카메라로부터 얻은 monocular RGB 이미지들만 요구한다.
• Multi view나 semantic prior를 요구하는 Yoon et al. [Yoon et al. 2020]과 같은 모델도 있지만 우리의 방법은 NeRF와 같이 입력으로 사용된 input sequence 외에 다른 학습 데이터를 요구하지 않는다.
• Neural Volumes: deformable scene들을 volumetric 3D voxel grid와 warp field를 사용하여 표현하며 이는 convolutional neural network에 의해 직접적으로 예측된다.
• Deformable NeRF technique과 Nerfies는 human subject들을 회복하며 넓은 범위의 non-stationary subject들에 대해 photorealistic synthesized view를 생성할 수 있다.
• 우리는 이 기법들 위에, 이를 확장하여 움직이고 변형이 있을 뿐 아니라 위상적으로 달라지는 물체들을 더 잘 표현한다.

2.2. Neural rendering

• 초기의 "neural rendering"은 neural network가 물체들의 이미지를 render하는 것을 목적으로 함.

• 지배적인 paradigm은 neural network가 scene의 이미지에 대한 일부 표현을 mapping하도록 학습되는 것이다.

• Neural rendering 연구는 "image to image translation"에서 "neural scene representation" 패러다임으로 옮겨가고 있다.

• Pixel intensity를 예측하는 black box neural network 대신에, scene 표현 접근법은 neural network의 weight를 사용하여 occupancy, distance, surface light field, latent representation 등 physical scene 자체를 직접적으로 모델링한다.

• 가장 효율적인 접근법은 scene의 neural radiance field를 구축하는 것으로 convolutional MLP를 사용하여 공간 scene 좌표 함수로서 volumetric density와 color를 파라미터화하는 것이다.

• NeRF로부터의 rendering은 하나의 일관된 geometry 모델에 대응하며 volumetric rendering의 gradient들은 gradient-based optimization에 잘 맞는다.

• NeRF 대신에 physics 기반의 volumetric rendering engine이 geometry와 radiance가 neural network에 의해 파라미터화된 scene을 render하기 위해 사용되었다.

• NeRF는 내용물들이 정적인 scene에 대해 강력한 성능을 보였지만 이는 움직이는 물체들이 있을 때 재앙적으로 실패했다.

• 최신 연구들은 NeRF가 dynamic scene들을 support하도록 확장되었고 이는 크게 deformation-based approaches와 modulation-based approaches로 나뉜다.

• Deformation 기반의 접근법

  • 공간적으로 달라지는 deformation을 canonical radiance field에 적용한다.
  • Nerfies, D-NeRF, NR-NeRF 등이 있고 이들은 모두 연속적인 deformation field를 정의하는데 이는 observation 좌표들을 template NeRF를 query하는 데에 쓰이는 canonical 좌표들로 mapping한다.
  • 다수의 관측들이 하나의 canonical template을 재구성하는 데에 쓰이고 deformation field가 이미지들마다 다르기 때문에 이 접근법은 basic NeRF와 같이 제한된 최적화 문제를 야기한다.
  • 그러나 scene의 연속적인 deformation field의 사용은 이 기법들이 topological variations (e.g, mouth openings)나 transient effects (e.g, fire)를 모델링할 수 없음을 의미한다.
  • Topological opening과 closing은 closing의 경계선이 deformation field에서 불연속성을 요구하는데 이는 쉽게 모델링할 수 없다.
  • 이는 positional eencoding을 가진 좌표 기반의 MLP가 nerual tangent kernels를 통해 봤을 때 band-limited kernel과 함께 interpolation을 수행한 결과이다.

• Modulation 기반 또는 latent-conditioned NeRF

  • 입력 이미지의 어떤 property에 대해 Scene의 radiance field를 직접적으로 조절하고 수정한다.
  • NeRF 변수들은 출력을 조절하기 위해 latent conde와 함께 neural network를 conditioning하는 기법을 채택했다.
  • Modulation 기반의 MLP는 각 이미지들을 설명하기 위해 warping되는 single NeRF로서의 scene을 모델링하는 것 대신 이미지의 timestamp나 latent code와 같은 추가적인 정보들을 MLP의 입력으로 넣어서 scene의 radiance field를 직접적으로 변화시켰다.
    
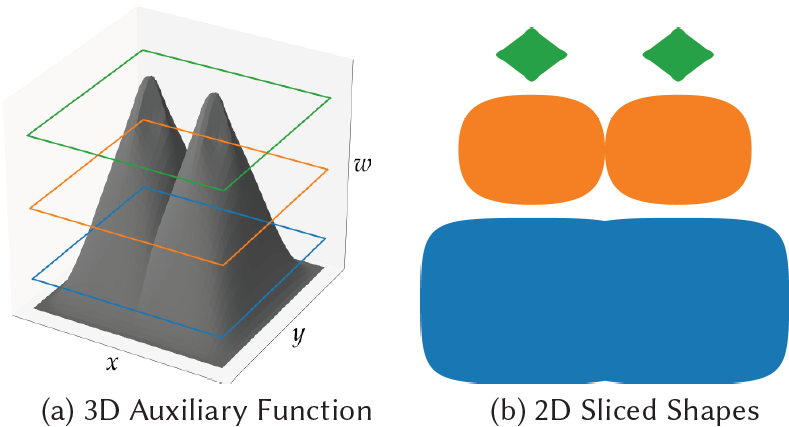
    Fig. 2. Level-set 방법들은 고차원의 auxiliary funciton (a)의 slice들인 (b)로서 topologically varying shapes의 family를 모델링하는 것의 수단을 제공한다.

• 이러한 modulated NeRFs들은 입력 이미지들마다 완전히 다른 radiance와 density를 가질 수 있으며 이 기법들은 심각하게 제한되지 않은 문제와 trivial, non-plausible solution들을 야기한다.

• 이러한 이슈들은 depth나 optical flow와 같은 추가적인 supervision을 제공하는 것(Video-NeRF [Xian et al. 2020]와 NSFF[Li et al. 2020]) 또는 7개의 synchronized camera들로부터 캡쳐된 multi-view input을 사용하는 것(DyNeRF [Li et al. 2021]) 의해 다뤄질 수 있다.

• Gafni et al. [2021]은 3D morphable face model로부터 face-centric coordinate frame을 사용하는 것에 의해 이 문제를 피했다. NeRF in the Wild는 비슷한 modulated 접근법을 사용했는데 이는 latent code들이 최적화되고 MLP의 입력으로 제공되었다. 또한 이는 ambiguity를 제공했으며 이 ambiguity는 density가 아닌 radiance만 수정하는 code들에 의해 다뤄졌다.

• 우리의 방법은 deformation 기반과 modulation 기반 접근법들의 조합으로 생각될 수 있다. 우리는 scene에서 motion을 모델링하는 데에 deformation을 사용했고 well-behaved optimization을 얻었다. 그러나 우리는 또한 NeRF의 3D 입력 좌표 공간을 추가적인 고차원 좌표들을 입력 받도록 확장했고 공간적 차원 뿐만 아니라 더 높은 차원을 따라 deformation을 허용했다.
  이 접근법은 deformation 기반의 접근법은 모델링할 수 없는 object topology에서 변화들을 포착하기 위해 더 높은 차원을 사용할 수 있게 했다.

  Deformation으로 motion modeling + 차원 확장을 통해 topology도 다룰 수 있음.

3. Modeling time-varying shapes

• 우리의 방법은 더 높은 차원의 입력과 함께 NeRF를 제공하는 것에 의해 scene topology에서 변화를 표현한다.
• Object의 surface를 수학적으로 표현하는 2가지 방법이 있다: surface는 poligonal mesh와 함께 explicit하게 표현될 수 있고 연속적인 함수의 level set으로서 implicit하게 표현될 수도 있다.
• Explicit representation들은 surface의 topological variation에 잘 맞지 않는다. 이러한 종류의 variation은 이러한 변형들이 불연속적이고 쉽게 미분가능하지 않아서 특히 NeRF와 같은 gradient-based optimization으로 표현하기 어렵다. 이와 대조적으로 implicit surface들은 surface가 hole로 발달하거나 다수의 piece들로 나뉘는 등 topological 변화들이 있을 때 surface의 발달을 모델링하는 자연스러운 방법을 제시한다.

3.1. Level set methods

• Level set method들은 예비 함수의 zero-level set으로서 surface를 implicit하게 모델링한다. 예를 들어 2D surface는
  
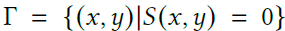
  $S: (x,y) \rightarrow s$는 signed-distance function으로 $s > 0$이 surface의 inside에 있는 point들이고 $s < 0$는 surface의 바깥 쪽에 있는 point들이다.

추가적인 차원 $w$를 더할 수 있고 우리는 3D surface를

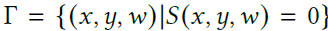
과 같이 정의한다.

• 우리는 추가적인 차원에 의한 공간을 "ambient" space라고 부른다.
• 주변 좌표 $w_i$ 에서 2D surface는 $w=w_i$를 통과하는 plane과 함께 이를 자르는 것에 의해 얻어지는 3D surface $\Gamma$의 2D cross-section으로서 표현된다.

3.2. Deformable slicing surfaces

• Level set 방법들은 axis-aligned plane과 함께 function을 slicing하는 것에 의해 동작한다.
• 이 slice의 plane은 공간적 축(2D/3D 예시에서 x와 y축)들을 포괄하며 모든 point들에서 하나의 주변 좌표 ($w$ 축)를 차지한다.
• Axis-aligned slice를 사용한 결과 모양은 slicing plane에 의한 cross section cut이다.

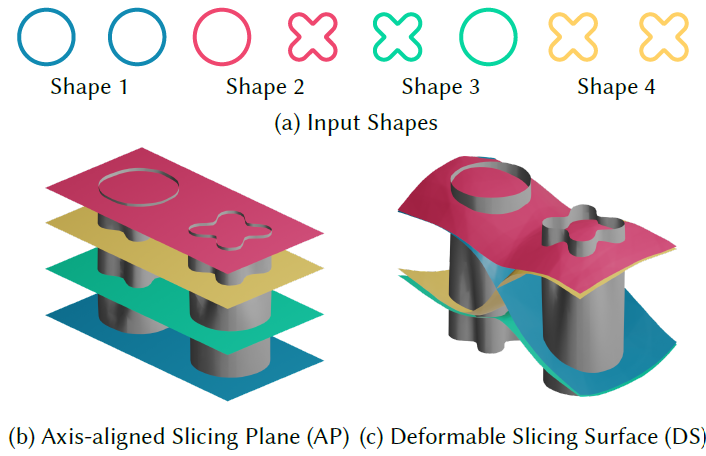
Fig. 3. 우리가 "ambient surface"라고 부르는 더 높은 차원의 surface의 slice로서 Level=set methods model shapes. 우리는 2개의 slicing method들을 제안함

• Axis-aligned planes (AP) slice
  • Surface가 더 높은 차원의 축과 수직이다.
• Deformable surfaces (DS)
  • 변형될 수 있고 shape의 다른 part들이 hyper-space의 변화하는 part들을 참고할 수 있다.
• Axis-aligned plane들은 각 shape의 copy를 독립적으로 요구하지만 deformable surface들은 정보를 공유하고 더 간단한 ambient surface들을 야기한다. 우리는 deformable slicing surface들을 MLP의 weights 안에서 encode한다.
  
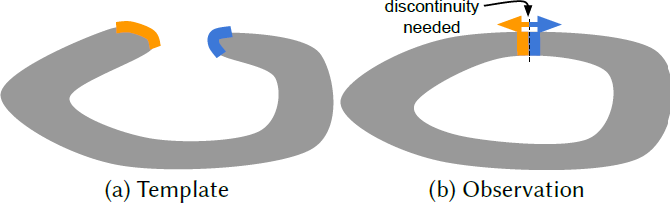
  Fig. 4. ring이 marked seam에서 열리는topological change의 예시. Observation frame에서 template을 참고하는 deformation field는 접합부에서 불연속성을 요구하여 orange position에서 blue position으로의 극소량의 step은 deformation에서 큰 변화를 낳는다.
  만약 template이 the closed ring이라면, contents는 deformation field를 사용하여 접근 가능하지 않다.
• 우리는 deformable slicing surface를 MLP $H: (x, \omega_i \rightarrow w)$로 정의한다.
  • $x$: spatial position
  • $w$: ambient axes를 따르는 position
  • $\omega_i$: per-input latent embedding
• SDF는 $x$와 $H(x, \omega_i)$를 concatenate하는 것에 의해 얻어지는 좌표에 대해 query된다.

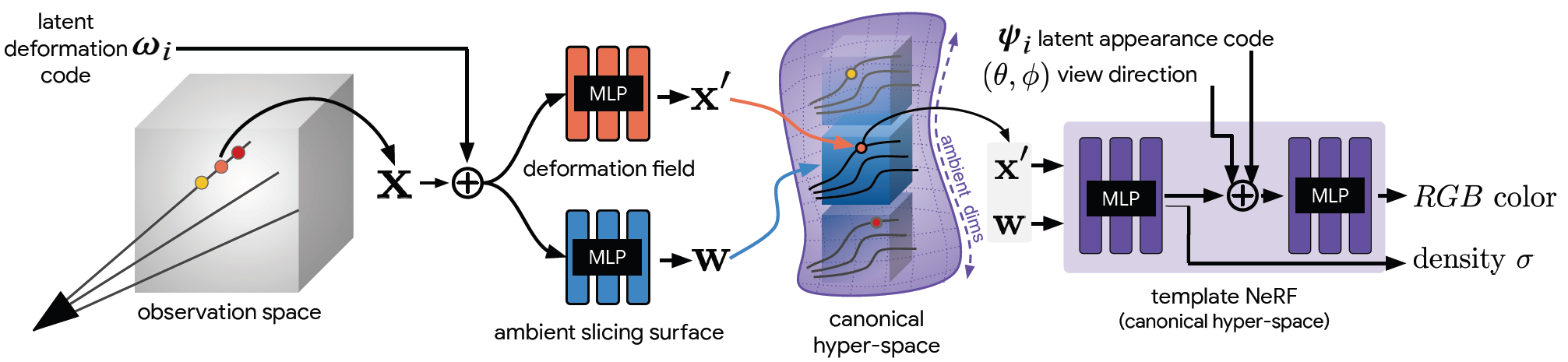
Fig. 5. 우리의 모델 구조의 overview. 우리는 latent deformation code $\omega_i$와 a latent appearance code $\psi_i$를 연관시킨다. Sample $x$는 latent deformation code $\omega_i$와 결합하여 deformaiton field를 파라미터화하는 MLP의 입력으로 들어간다.

• 이 MLP는 warped coordinate $x'$과 ambient space $w$에서의 좌표 $w$를 내보낸다.
• $(x', w)$의 concatenation과 viewing direction $d = (\theta, \phi)$, 그리고 appearance code $psi_i$가 template NeRF를 파라미터화하는 MLP의 입력으로 사용된다.
• MLP에 의해 생성된 color와 density는 Volumetric rendering의 physics의 ray를 따라 통합된다.

4. Method

• 우리는 casually captured monocualr image 시퀀스들이 주어졌을 때, non-rigidly deforming scene들을 모델링하는 우리의 방법을 묘사한다.
• 우리의 method의 focus는 topologically 변화하는 scene에서 appearance와 geometry를 정확하게 모델링할 수 있게 하는 것이다.

4.1. Review of NeRF, NeRF-W, and Deformable NeRF

• NeRF는 scene을 연속적이고 volumetric field of density and radiance로 표현하며 이는 다음과 같이 정의되어 있다.
  • $F: (x, d, \psi_i) \rightarrow (c, \sigma)$
  • The function $F$는 MLP에 의해 파라미터화 되어 3D position $x$와 viewing direction $d$를 color $c$와 density $\sigma$로 mapping한다.
• NeRF는 입력 좌표를 직접 MLP에 넣지 않고 input $x$와 $d$를 sinusoidal positional encoding을 사용하여 mapping한다.
  
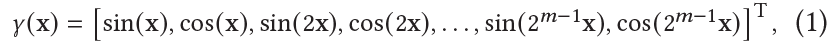
  • $m$: a hyper parameter로 encoding에 의해 사용된 sinusoid들의 수를 control함
  • 이 encoding은 MLP가 high-frequency signal들을 low frequency domain에서 모델링할 수 있게 해주며 parameter $m$은 an interpolated kernel의 효율적인 bandwidth를 조절하는 것에 의해 학습된 표현의 smoothness를 control하는 역할을 한다.
• Appearance variation
  • 관측된 각 frame $i \in \{1, ..., n\}$에 대해 An appearance embedding $\psi_i$는 조명 변화나 노출 변화, 그리고 white balance 등과 같이 input frames 사이의 appearance vairation들을 다룰 수 있게 해준다.
• Deformations
  • 우리는 non-rigid motion을 모델링하기 위해 Nerfies에 의해 제안된 deformation field formulation을 사용한다.
  • Deformation이 rigid하도록 하기 위해 Nerfies는 the deformation field의 Jacobian의 non-unit singular values 값에 penalty를 가하는 elastic regularization loss를 도입했다.
• Windowed Positional Encoding
  • Positional encoding $\gamma$에서 frequency의 수 $m$은 MLP의 Neural Tangent Kernel (NTK)의 bandwidth를 control한다.
• Window 함수는 다음과 같다.
  
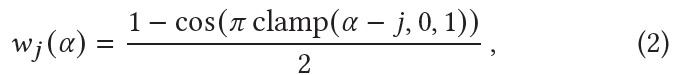
  • $j \in \{0, ..., m-1\}$는 positional encoding의 frequency band이다.
• The windowed positional encoding은 다음과 같이 계산된다.
  
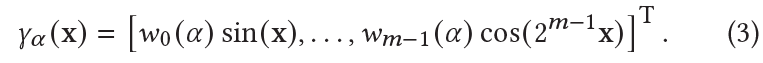
• Nerfies는 이것을 deformation field를 coarse-to-fine 방식으로 최적화하기 위해 사용하며 이는 high-frequency deformation을 표현하는 능력을 유지하면서 sub-obtimal local minima에 빠지는 것을 방지한다.

4.2. Hyper-space Neural radiance fields

• Motion은 2가지로 나뉠 수 있다.

  • (a): scene의 topology를 유지하는 motion
  • (b): scene의 명백한 topology를 변화시키는 motion

• Deformation fields는 topology를 유지하는 motion을 효율적으로 모델링할 수 있지만 topology에서의 변화를 쉽게 모델링하지 못한다.

  • 이는 topology에서의 변화가 deformation field에서의 불연속성을 포함하고 deformation fields는 이러한 불연속성을 표현할 수 없기 때문이다.
    
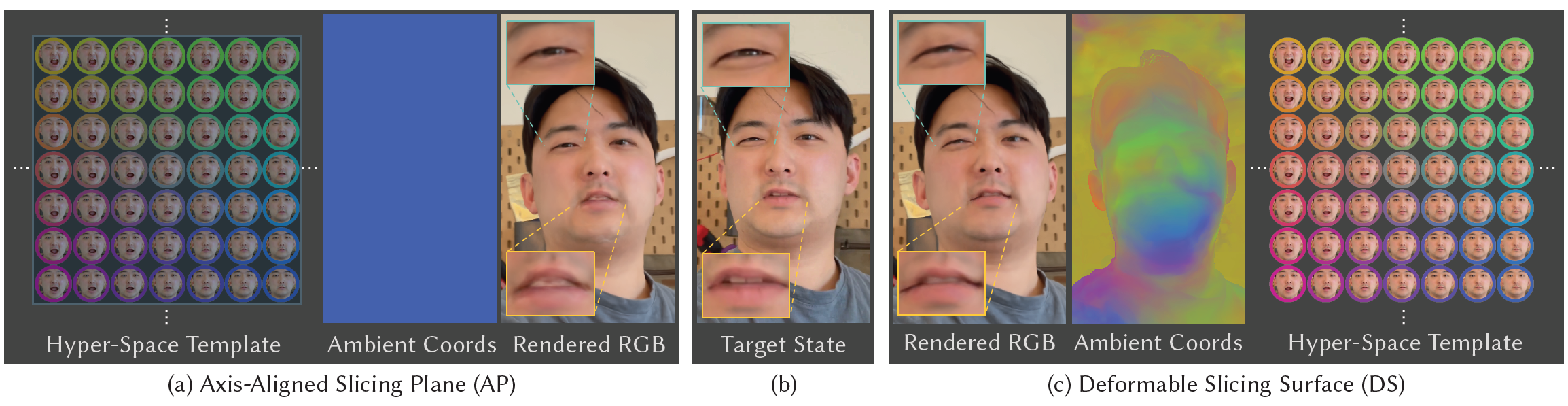
    Fig. 6. 우리는 axis-aligned slicing planes (AP, a)와 deformable surfaces (DS, c)로부터 얻은 target state를 rendering한다.

• 더 높은 차원의 ambient surface의 cross section으로서 topologically 변화하는 shape들을 자연스럽게 모델링할 수 있는 level set method를 도입했다.

• Hyper-space Template

  • 우리의 idea는 template NeRF를 더 높은 차원에서 embedding하는 것으로 높은 차원의 slicing surface를 가로지르는 것에 의해 취해진 slice가 full 3D NeRF를 생성한다.

• 우리는 template NeRF를 더 높은 차원의 공간으로 확장한다.

  • $(x, w) \in \R^{3+W}$, $W$: 더 높은 차원의 수

• Template NeRF의 formulation은 다음과 같이 MLP로 표현된다.
  

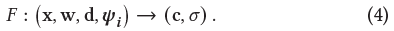
Slicing Surfaces

• Fig. 3에서 우리는 3D auxiliary surface는 2D shape을 얻기 위해 잘라질 수 있음을 보여주었고 같은 방식으로 우리는 hyper-space NeRF의 cross-sections을 취할 수 있다.

• 2D axis-aligned slicing plane (AP)와 유사하게, 우리는 ambient coordinates $\{w_i\}$에 의해 최적화된 observation $i$에서 template의 특정 slice를 deformation과 appearance code들과 연관시킨다.

• 이러한 접근법은 관측에 대한 모든 ray sample들이 같은 ambient 좌표들을 공유하도록 하고 모든 관측된 상태들이 하나의 ambient coordinate에 대해 explicit하게 모델링되도록 하는 것을 요구한다.

• 각 observation-space sample point $x$는 mapping $H: (x, \omega_i) \rightarrow w$를 사용하여 mapping된다.

  • $\omega_i$: latent deformation code
  • w: sample을 위한 cross-sectional subspace를 정의하는 ambient 좌표 공간에서의 point

• Template NeRF $F$, the spatial deformation field $T$, 그리고 the slicing surface field $H$가 주어졌을 때, the observation-space radiance field는 다음과 같이 평가된다.
  

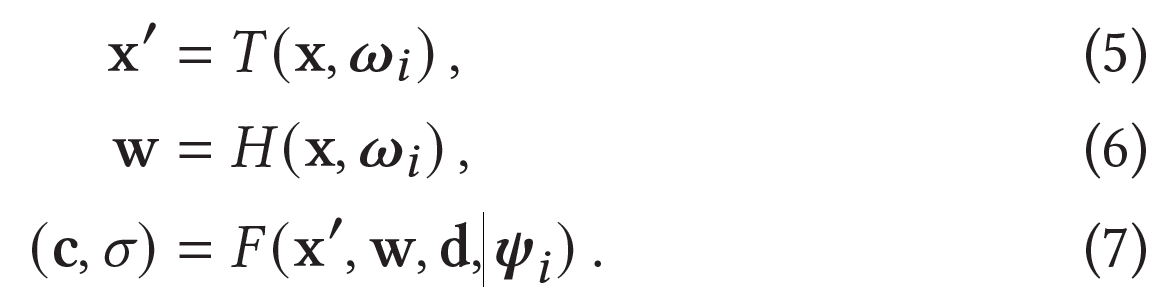
• $\gamma_\alpha$: windowed positional encoding for the deformation field $T$

• $\gamma_\beta$: windowed positional encoding for the slicing surface field $H$

Fig. 7. "Expression 1"으로부터 2개의 프레임들의 embedding $\omega_i$를 interpolate하는 것에 의해 합성된 Novel views. AP를 사용했을 때, 모든 공간적 point들은 같은 ambient 좌표에서 rendering되었고 interpolation 중에 blurry-cross fading artifacts들을 야기했다. DS를 사용했을 때, ambient의 다양한 part들을 참조하는 다른 공간적 position들은 더 나은 interpolation을 보여주었다.

5. Experiements

5.1. Implementation details

• 우리의 NeRF와 deformation field의 시행은 Nerfies를 따른다.
• 우리는 L2 photometric loss를 사용하며 8차원의 latent appearance와 deformation code를 사용한다.
• JaxNeRF를 바탕으로 실행헀고 우리는 1080p resolution의 절반을 250k iteration에 대해 학습했고 6144 batch size와 함께 128개의 sample을 사용했으며 이는 4개의 TPU를 사용하여 8시간 소요되었다.

5.2. Evaluation

5.2.1. Quantitative Evaluation

• 우리는 우리의 방법을 2가지 task들에 대해 평가했다.

  • 얼마나 이것이 학습 과정 중 visual plausibility를 유지하면서 다른 moment들 사이에 interpolate하는지를 펻가
  • 이것이 novel view synthesis를 하는 능력을 평가

• 우리는 LPIPS, MS-SSIM, 그리고 PSNR을 사용하여 visual quality를 측정했다.

  • 우리는 3가지 중 LPIPS가 perceptual quality를 가장 잘 반영하는 것을 알아냈다.
    
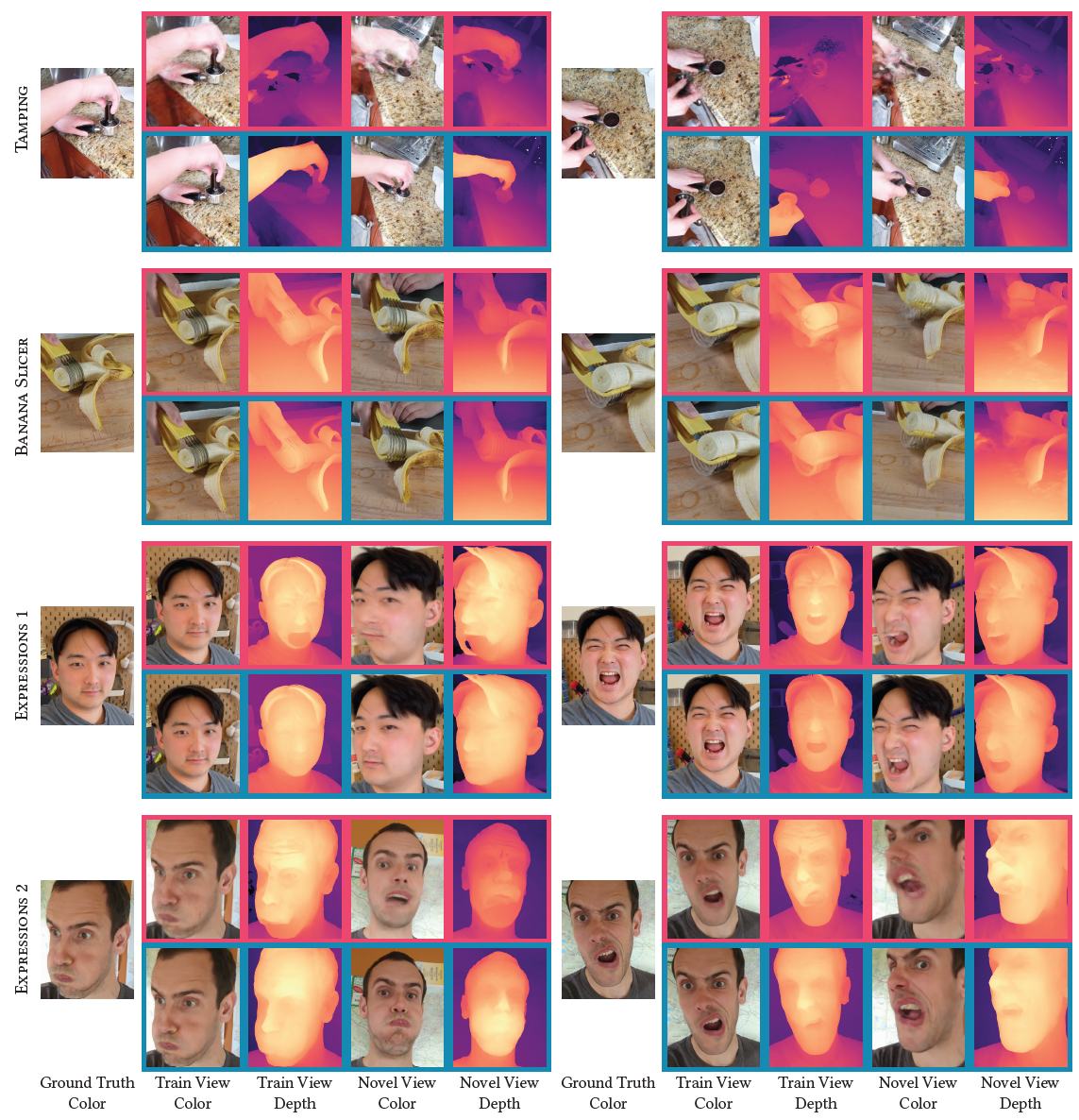
    Fig. 8. 우리는 4개의 다른 시퀀스들에 대해 Nerfies와 HyperNeRF의 질적인 비교를 보여준다.

• Nerfies는 deformation field로 topological variation을 모델링할 수 없어 학습 데이터를 설명하기 위해 geometry를 implausible한 방식으로 왜곡하지만 HyperNeRF는 더 그럴듯한 geometry 예측과 학습 중 보지 못한 novel view에 대해 더 정확한 rendering을 생성한다.

Fig. 9. Topology에서 기술적 변화가 없더라도, base에 대해 상대적으로 움직이는 3D printer의 bed는 deformation field에서 sharp한 변화를 요구하며 geometry에서 artifact를 만든다. HyperNeRF는 이를 완화한다.

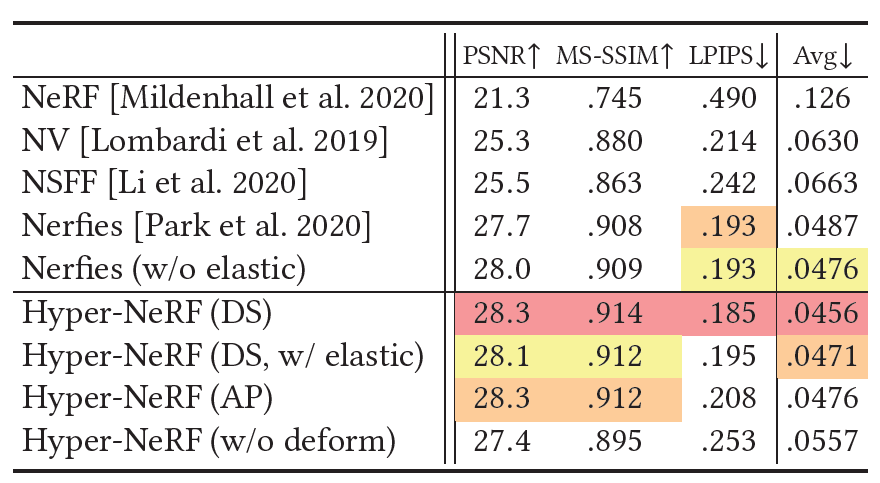
Table 1. 모든 시퀀스들에 대해 평균된 Interpolation task에 대한 Metrics. 우리는 PSNR, MS-SSIM, 그리고 평균 metric of Barron et al.을 보고한다.

• 우리는 우리의 방법을 Nerfies, Neural Volumes, 그리고 NSFF와 비교했다.
• Neural Volumes에 대해, 우리는 encoder를 사용하여 2개의 reference frame을 encoding하는 것에 의해 interpolated frame을 rendering했다.
• NSFF에 대해, 우리는 2개의 reference frame들 사이의 input time variable을 선형적으로 interpolate했다.
• Table 1은 우리의 방법이 대부분의 case들에 대해 baseline들을 압도함을 보여준다.

Novel-view synthesis

• 우리는 topologically 변하는 scene들에 대해 우리의 방법의 novel view synthesis quality를 평가한다.
• 우리는 unseen viewpoints로부터 고정된 moments에서 scene을 rendering하고 예측된 이미지들이 대응하는 ground truth 이미지와 얼마나 잘 match되는지 비교한다.
• 우리는 BROOM 시퀀스를 broom이 땅에 닿을 때 topological change들을 보여주는 BROOM sequence에 대해 평가했으며 3D PRINTER, CHICKEN< EXPRESSIONS, 그리고 PEEL BANANA의 4가지 추가적 시퀀스들과 함께 augment된 시퀀스들에 대해 평가를 진행했다.

Baselines

• View-synthesis를 위해, 우리는 NeRF, Neural Volumes, 그리고 2개의 최신 dynamic NeRF methods인 NSFF, Nerfies를 비교했다.
• 우리는 각 image encoder에 validation image에 대응하는 학습 이미지들의 latent code를 계산하고 encoding vector를 선형적으로 interpolate했다.
• 우리는 Neural Volumes에 대해 central crop에 대해 error metrics만 비교했으며 Yoon et al [2020]에 대해 향상된 결과를 보여준 NSFF와 비교했다.

5.2.2. Qualitative results

• Fig. 8은 우리의 방법을 Park et al.과 비교하여 질적인 결과를 보여준다.
• Nerfies는 few artifacts를 제외하고 sharp results를 생성했지만 우리의 방법은 PEEL BANANA and EXPRESSIONS와 같은 scene들에 대해 object의 pose를 더 잘 reconstruct한다.

6. Limitations and conclusion

• NeRF-like methods 뿐만 아니라, camera registration도 reconstruction의 quality에 영향을 준다.
• 우리의 모델은 domain-specific priors 없이 color 이미지만 입력으로 사용하므로 관측된 것만 reconstruct할 수 있다.
  • 학습 데이터에서 잘 capture되지 않은 순간들은 우리의 방법으로 재구성될 수 없다.
• 우리는 HyperNeRF를 불연속적인 deformation과 함께 topologically varying scene들을 reconstruct하는 NeRF의 확장으로서 제시한다.
• Deformation 기반의 dynamic NeRF 모델은 MLP의 weights에 encode된 연속적인 deformation fields의 사용 때문에 topological variations을 모델링할 수 없다.
• HyperNeRF는 더 높은 차원의 공간을 통한 slice로서 이 variation들을 모델링한다.
• 공간을 compact하게 유지하고 overfitting을 피하기 위해, 우리는 ambient 차원의 사용을 지연시켰으며, 이 slice들을 사용하기 위해 deformable hyperplanes를 사용한다.
• 그러고 나서 우리는 level-set 방법들과 deformation 기반의 dynamic NeRF 모델들로부터의 insight를 결합하고 large motion들과 topological variation 모두에 대해 reconstruct한다.
  
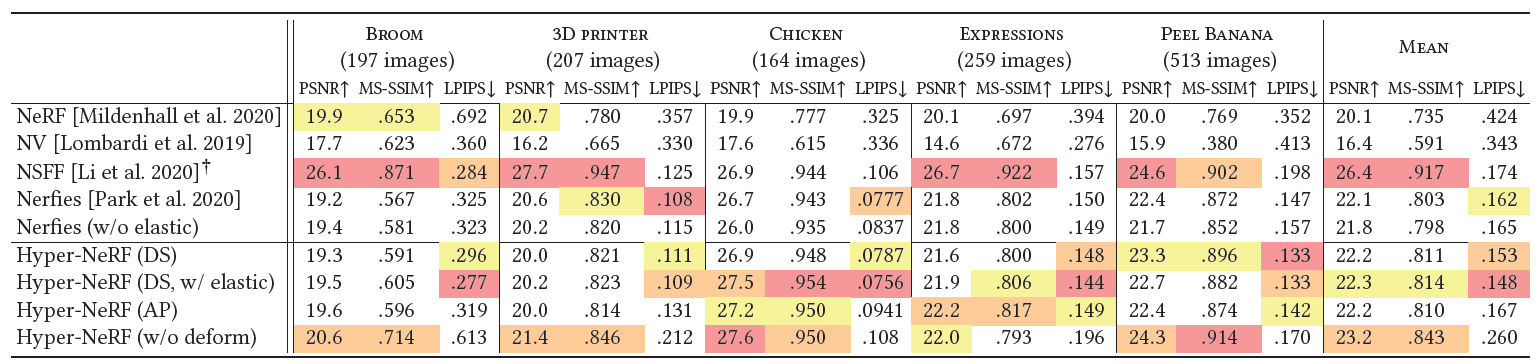
  Table 2. rig captures에 대한 양적인 평가. 우리는 우리의 방법의 baseline과 ablation들을 비교했다.

Fig. 10. rig scene들에 대한 우리의 방법의 baseline들의 비교. PSNR/LPIPS metrics의 best 값은 red로 표시했으며 baseline들은 Nerfies, HyperNeRF without deformations, Neural Volumes, NSFF, 그리고 NeRF가 있다.

Fig. 11. Interpolation dataset에 대한 우리의 방법, ablations, 그리고 baseline들에 대한 질적 비교.

• The interpolated frame은 2개의 reference frame들의 latent code들 사이의 linearly interpolating에 의해 rendering된다.
• Baseline들은 다음과 같다: Nerfies, Neural Volumes, NSFF, 그리고 NeRF
  Fig. 12. interpolation dataset에 대한 우리의 방법, ablations, 그리고 baseline들에 대한 질적 비교. The interpolated frame은 두 latent frame들의 latent code 사이를 interpolate하는 것에 의해 rendering된다. 각 시퀀스들의 bottom row는 absolute error를 나타내며 baseline들은 Nerfies, Neural Volumes, NSFF, 그리고 NeRF이다.

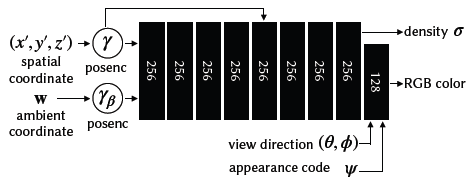
Fig. 13. A diagram of our hyper-space template network로 original NeRF MLP와 동일하지만 이것은 추가적인 ambient coordinate와 appearance latent code $\psi$를 입력받는다.

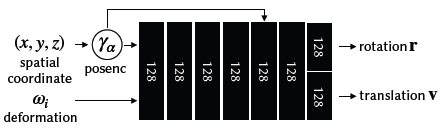
Fig. 14. 우리의 deformation network의 diagram으로 이는 Nerfies의 deformation MLP와 동일하다.

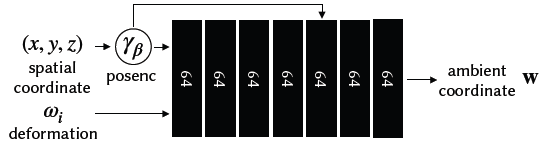
Fig. 15. 우리의 ambient slicing surface network의 diagram. 이는 deformation network와 input deformation code $\omega_i$를 공유한다.
The ambient slicing surface network는 다른 windowed positional encoding parameter $\beta$를 쓰고 ambient coordiante $w$를 출력한다.

A. Network architecture

• 우리는 template MLP를 위한 detailed architecture digram을 제공하며, Fig. 13에서 template MLP, Fig. 14에서 deformation MLP, Fig. 15에서 ambient slicing surface MLP를 제시한다.

B. Evaluation

B.2. Additional quantitative metrics

• 우리는 interpolation task를 위해 per-sequence evaluations metrics를 제시한다.
  • LPIPS, MS-SSIM, 그리고 PSNR을 기록했다.

B.3. Details of the NSFF experiments

• Template MLP는 다음과 같다.
  

• 입력: 2D 좌표 $(x,y) \in [-1, 1]^2$, an ambient coordinate $w \in \R$, 그리고 출력인 a signed distance $s$.

• 이 함수는 3D surface를 정의하며 이는 slicing surface에 의해 잘라진다.

• Ambient slicing surface MLP는 다음과 같다.
  

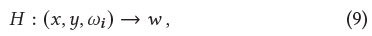
• $\omega_i$: per-shape latent code

• $w$: output ambient coordinate

Training

• Training batch들의 학습은 각 shape $i$의 연속적이고 truncated SDFs에서 랜덤으로 point들을 샘플링하는 것에 의해 생성되었으며 그 형태는 다음과 같다.
  ${((x,y,\omega_i), s)}$
• 우리는 Pseudo-Huber loss function을 사용한다.
  
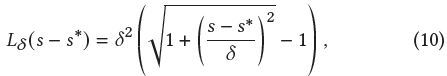
• $s$: 예측된 SDF 값으로 $s^{*}$ 은 ground truth SDF 값이다.
• $\delta$: Steepness를 control하는 hyper-parameter

Implementation Details

• 우리는 positional encoding을 minum degree와 maximum degree에 대해 사용했다.
  
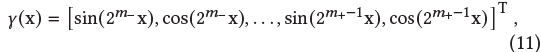
• $m_{-}$: minimum degree
• $m_{+}$: maximum degree

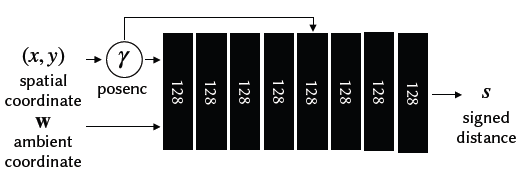
Fig. 16. 2D level set 실험에서 2D template NeRF를 위한 diagram 구조

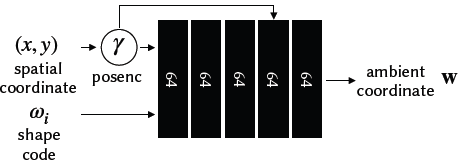
Fig. 17. 2D level set 실험에서 사용된 ambient slicing surface MLP를 위한 diagram 구조

• 우리는 batch size 512와 함께 2000 iterations를 도는 learning rate $10^{-3}$과 함께 Adam optimizer를 사용하여 학습했다.

Interpolating shapes

• 우리는 instance들마다 shape code $\omega_i$를 선형적으로 interpolate하는 것에 의해 interpolated shape을 생성했다.

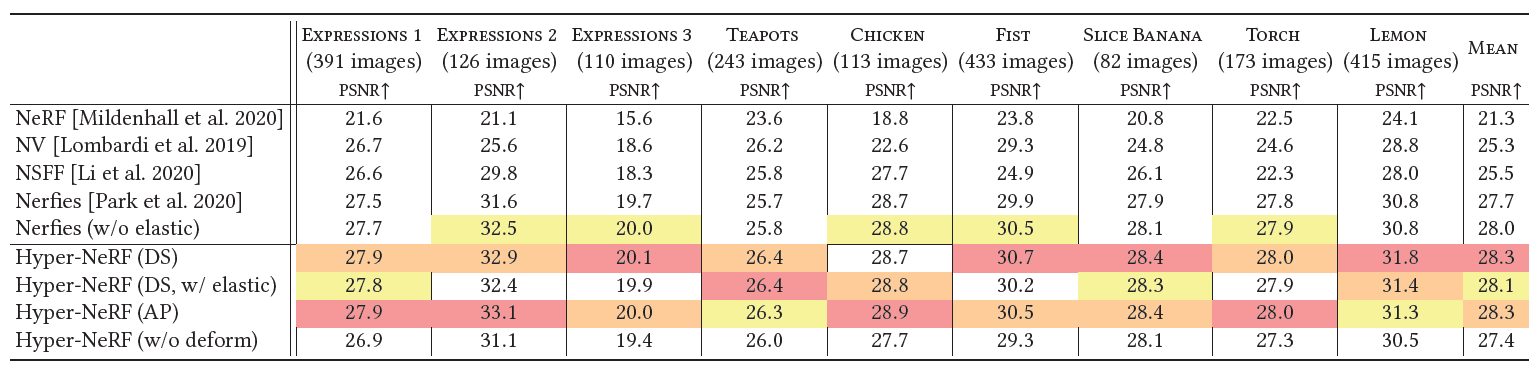
Table 3. Per-sequence PSNR metrics on the interpolation task.

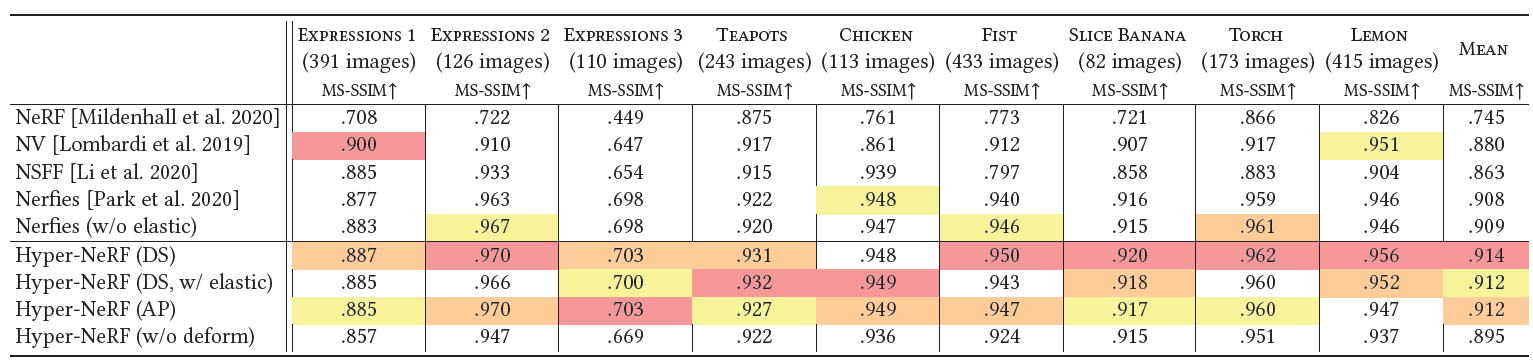
Table 4. Per-sequence MS-SSIM metrics on the interpolation task.

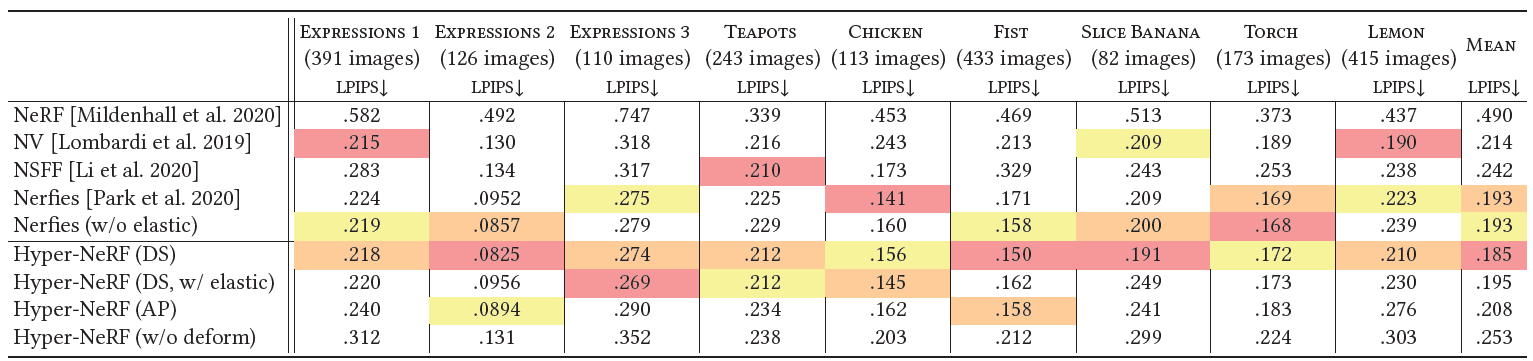
Table 5. Per-sequence LPIPS metrics on the interpolation task.

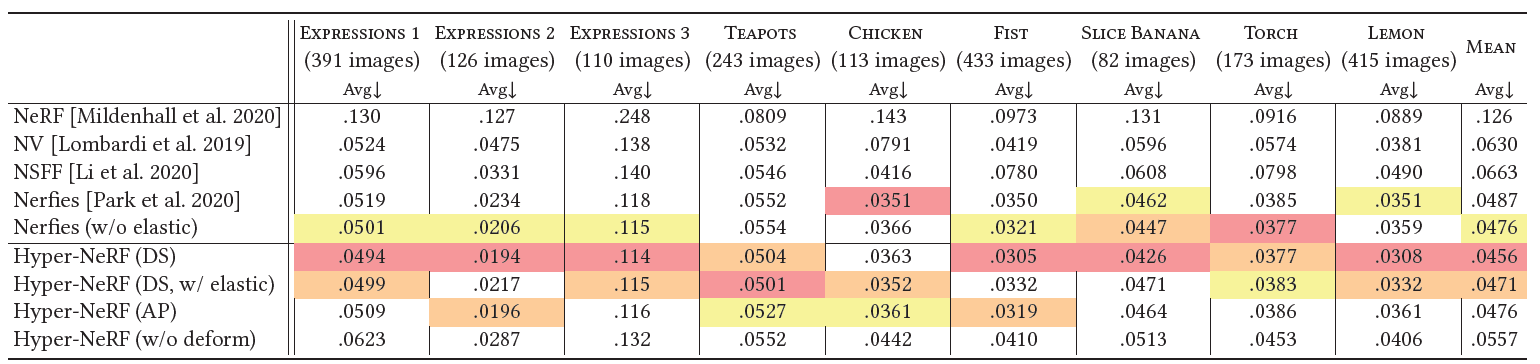
Table 6. Per-sequence "average" metrics on the interpolation task.