VAE란?
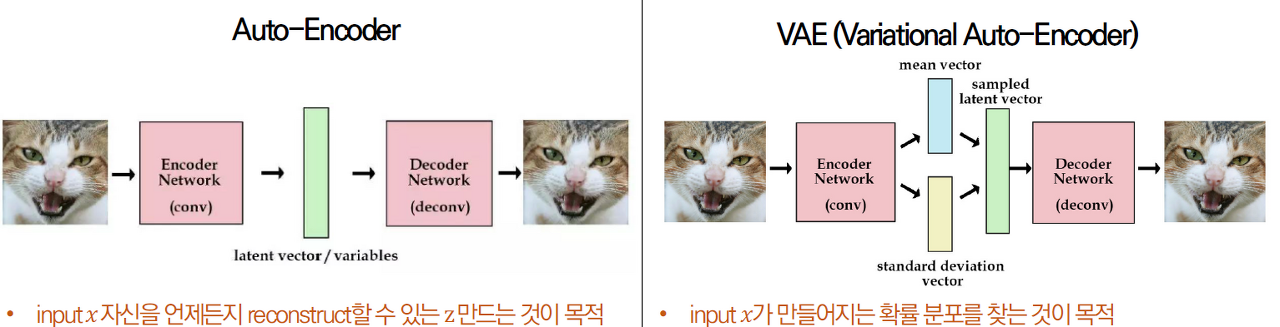
AE와 VAE의 차이점은 AE는 잠재공간 z에 값을 저장하고 VAE는 확률 분포를 저장하여 (평균, 분산) 파라미터를 생성한다는 점이다.
VAE 전체적인 작동 흐름
VAE의 decoder는 encoder가 만들어낸 z의 평균, 분산을 모수로 하는 정규분포를 전제하고 데이터의 사후확률 p(z|x)를 학습한다. 하지만 사후확률의 계산이 어렵기 때문에 다루기 쉬운 분포 q(z)로 근사하는 variational inference (변분추론)을 사용한다. 변분추론은 p(z|x)와 q(z)사이의 KL-Divergence를 계산하고, KLD가 줄어드는 쪽으로 q(z)를 조금씩 업데이트 해서 q(z)를 얻어낸다.
아래 식은 데이터가 고차원인 경우 q학습이 어렵다. 복잡한 데이터에 비해 지나치게 단순한 모델이기 때문.
1) q(z) = N(평균,분산)
그래서 q의 파라미터를 x에 대한 함수로 한다. 이렇게 설정하고 ELBO를 구하면 x가 달라질 때마다, q의 분포가 달라짐. (q의 모수인 평균 분산이 바뀌기 때문)
2) q(z|x) = N(평균(x),분산(x))
따라서, encoder는 x를 받아서 z의 평균, 분산을 만들어내는 두개의 뉴럴 네트워크를 포함하여 복잡한 데이터에 대해 적절한 모델을 적용할 수 있다. 추가로, z를 생성하는 과정을 설명하면, zero-mean Gaussian에서 노이즈를 하나 뽑아 평균 분산을 더하고 곱하여 z를 샘플링한다. 주의할 점은 데이터에서 직접 샘플링 하는 것이 아니라 노이즈를 샘플링 하기 때문에 동일한 데이터 x가 들어가더라도 얼마든지 다른 z가 나올 수 있다. (그래서 variational이 붙었다고 한다.)
VAE 수식 유도 - 사전지식
1. Jensen's inequality
- 볼록함수에 대하여, 어떤 값들의 평균을 함수에 대입한 결과는 각각의 값을 합수의 대입한 값의 평균보다 항상 작거나 같다.
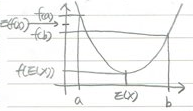
“ 볼록함수 𝒇와 적분가능한 확률변수 𝑿에 대해, 𝑬(𝒇(𝑿)) ≥ 𝒇(𝑬(𝑿))가 성립한다”
2. KL-Divergence
- 두 확률분포의 차이를 계산하는 함수
Q(사전확률분포, 가설모델)->P(사후확률분포, 실제관찰 데이터) : KLD 최소화 학습
= 두 확률분포의 차이를 최소화하여 가설모델이 실제 데이터에 근사하게 만든다
3. Monte-Carlo Method
-
랜덤표본을 뽑아 함수의 값을 확률적으로 계산하는 방법(값을 근사)
-
MLE 식에서 적분을 계산하지 않고 sampling을 통해 추정(Estimate)
4. Bayes' Rule - 조건부 확률
5. Variational Inference (Variational Bayesian Method)
계산이 어려운 사후확률분포 P(x)를 추정하기 위해 다루기 쉬운 분포 Q(x) (가우시안 분포)를 가정하고, 이 확률분포 Q(x)의 모수를 바꿔가면서 이상적인 확률분포에 근사하게 만들어 Q(x)를 P(x)대신에 사용하는 방법
-
Monte-Carlo Method를 활용하면 Q(z)로 어떤 분포든 사용할 수 있음
-
VAE는 Monte-Carlo Method를 KLD에 적용하여 KLD 근사값을 최소로 하는 평균 분산을 구하고, 이렇게 구해진 정규분포가 Variational Inference의 결과
6. ELBO (Evidence Lower Bound)
- ELBO 수식 유도
-
ELBO 풀이 ①

1번 풀이는 Jensen's Inequlity를 통해 부등식을 만들어 ELBO를 구하는 풀이이다. -
ELBO 풀이 ②

2번 풀이를 통해 Log(P(x))를 maximize하려면 ELBO는 최대화 KLD는 최소화 해야 한다는 것을 알 수 있다
*P(x) : 우리 원하는 출력인 x가 나올 확률 (maximize 해야함)
Loss Function 손실함수

딥러닝 모델은 손실함수를 목적함수로 쓰는 경향이 있기 때문에 ELBO에 음수를 취하여 최소화
<참조>
hugrypiggykim.com/2018/09/07/variational-autoencoder%EC%99%80-elboevidence-lower-bound/
ratsgo.github.io/generative%20model/2018/01/27/VAE/
.png)
