문제
https://www.acmicpc.net/problem/2618
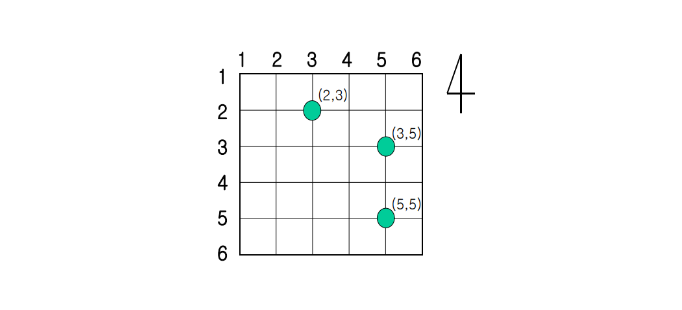
경찰차 1이 (1, 1)에 있고 경찰차 2가 (N, N)에 위치할 때, 각 사건(초록점)에는 경찰차 1대가 출동하여 사건을 해결할 수 있으며 해당 사건을 해결한 경찰차는 사건이 발생한 위치에서 기다리게 됩니다.
사건이 순서대로 주어졌을 때 두 대의 경찰차들이 이동하는 거리의 합의 최솟값을 구하는 문제입니다.
문제 핵심
-
경찰차 (y1, w1), 사건 위치(y2, w2)라 하였을 때 경찰차와 사건 사이의 거리는
|y2-y1| + |w2-w1|입니다. -
완전탐색으로 접근하되, 메모이제이션을 활용하여 시간복잡도를 줄여야 됩니다.
-
경찰차가 2대이므로 DP를 다음과 같이 정의할 수 있습니다.
DP [경찰차 1이 마지막으로 해결한 사건번호][경찰차 2가 마지막으로 해결한 사건번호]
본인이 처음 시도한 방식 (넘어가셔도 됩니다)
#include<bits/stdc++.h>
using namespace std;
int n, w;
vector < pair<int, int>> cases;
bool visited[1001][2];
int police[1001];
int result[1001];
int minResult;
void dfs(int cnt, int firstPolice_Y, int firstPolice_X, int secondPolice_Y, int secondPolice_X, int total) {
if (total > minResult) return;
if (cnt == w) {
if (minResult > total) {
minResult = total;
for (int i = 0; i < cnt; i++) {
result[i] = police[i];
}
}
minResult = minResult > total ? total : minResult;
return;
}
int nextY = cases[cnt].first - 1; // 입력 좌표 - 1
int nextX = cases[cnt].second - 1;
if (!visited[cnt][0]) {
visited[cnt][0] = true;
police[cnt] = 1;
// 경찰차 1의 현재거리에서 다음사건까지의 거리
int firstPoliceDistance = abs((firstPolice_Y - nextY) + (firstPolice_X - nextX));
// 경찰차 1 이동
dfs(cnt + 1, nextY, nextX, secondPolice_Y, secondPolice_X, total + firstPoliceDistance);
visited[cnt][0] = false;
}
if (!visited[cnt][1]) {
visited[cnt][1] = true;
police[cnt] = 2;
// 경찰차 2의 현재거리에서 다음사건까지의 거리
int secondPoliceDistance = abs((secondPolice_Y - nextY) + (secondPolice_X - nextX));
// 경찰차 2 이동
dfs(cnt + 1, firstPolice_Y, firstPolice_X, nextY, nextX, total + secondPoliceDistance);
visited[cnt][1] = false;
}
}
int main() {
cin >> n >> w;
for (int i = 0; i < w; i++) {
int y, x;
cin >> y >> x;
cases.push_back({ y, x });
}
minResult = INT_MAX;
dfs(0, 0, 0, n - 1, n - 1, 0);
cout << minResult << endl;
for (int i = 0; i < w; i++) {
cout << result[i] << endl;
}
}처음 접근할 당시에는 DP를 어떻게 정의할지 감이 안와 재귀 함수의 매개변수에 좌표와 거리의 합을 담아 구해나가는 완전 탐색으로 구현하였습니다.
이제 완전탐색을 수행하면서 중복된 부분을 찾아 메모이제이션을 하면되는데.. 그렇게 실행하려면 dfs 재귀함수가 거리의 최솟값을 반환하도록 하여 이를 메모리에 담는 구조인 Top-Down 방식으로 구현해야 했습니다.
이제 DP를 정의하면 되는데 각 사건을 어떤 경찰차가 담당했는지에 대한 기록도 필요하므로 DP를 비트마스킹으로 나타내야하나?하는 고민도 해보았지만 도저히 답이 안보여 인터넷을 참고하였습니다
정답 코드
#include<bits/stdc++.h>
#define p pair<int, int>
using namespace std;
int n, w, dp[1001][1001], cache[1001][1001];
vector<p> v;
int d(int a, int b) {
return abs(v[a].first - v[b].first) + abs(v[a].second - v[b].second);
}
int getSum(int a, int b) {
if (a == w + 1 || b == w + 1)
return 0;
if (dp[a][b] != 0)
return dp[a][b];
int nextCase = max(a, b) + 1;
int g = getSum(a, nextCase) + d(b, nextCase);
int h = getSum(nextCase, b) + d(a, nextCase);
if (g < h) {
cache[a][b] = 2;
}
else {
cache[a][b] = 1;
}
dp[a][b] = min(g, h);
return dp[a][b];
}
void solve() {
int a = 0, b = 1;
for (int i = 2; i < w + 2; i++) {
int nextCase = max(a, b) + 1;
if (cache[a][b] == 1) {
cout << "1" << endl;
a = i;
}
else {
cout << "2" << endl;
b = i;
}
}
}
int main() {
cin >> n >> w;
v.push_back({ 1, 1 });
v.push_back({ n, n });
for (int i = 0; i < w; i++) {
int a, b;
cin >> a >> b;
v.push_back({ a, b });
}
cout << getSum(0, 1) << endl;
solve();
}DP를 앞서 문제 핵심에서 설명한 것과 같이 정의합니다.
DP [경찰차 1이 마지막으로 해결한 사건번호][경찰차 2가 마지막으로 해결한 사건번호]
그리고 사건의 좌표를 사건 번호로 인덱스화 시키기위해 벡터를 선언하고 0번과 1번 인덱스에는 경찰차 1과 경찰차 2의 초기 위치를 담도록 해줍니다. 그리고 사건은 2번부터 w+2번까지로 정의됩니다.
이제 재귀 함수 getSum()을 살펴보겠습니다.
인자에는 메모이제이션을 수월히 수행하기위해 DP 정의와 같도록 경찰차 A와 경찰차B가 해결한 사건 번호가 담기게 해줍니다.
먼저 기저사례 정의와 중복처리부터 해줍니다.
int nextCase = max(a, b) + 1;그리고 a와 b 중 큰 값이 가장 최근에 해결한 사건 번호이므로 위 코드에서와 같이 다음 사건의 번호를 계산해줍니다.
int g = getSum(a, nextCase) + d(b, nextCase);
int h = getSum(nextCase, b) + d(a, nextCase);d 함수는 두 개의 인자에 사건 번호를 받고 인자로 받은 두 사건 간의 거리를 반환해주는 함수입니다.
위 코드는 완전 탐색을 수행하기 위한 코드로 변수 g에는 경찰차B가 다음 사건을 해결한 경우의 총 거리 합의 최솟값이 담기고, 변수 h에는 경찰차 A가 다음 사건을 해결한 경우의 총 거리 합의 최솟값(h)이 담기도록 해줍니다.
if (g < h) {
cache[a][b] = 2;
}
else {
cache[a][b] = 1;
}
dp[a][b] = min(g, h);
return dp[a][b];
최소 거리의 합을 구하는 문제이기에 g, h 이둘 중 더 작은 값을 DP의 현재 좌표에 저장해주고, 각 사건을 담당한 경찰차를 출력해주기 위해 cache 배열에 따로 경찰차 번호를 할당해주고 DP 배열의 현재 좌표에 담긴 값을 반환해줍니다.
인터넷에 정답 코드를 보고도 이해하는데 시간이 걸린 문제였습니다. 먼저 DP 정의를 보고 생각했던 것과 너무 달라 한-숨밖에 나오질 않았고 완전 탐색을 수행하는 로직도 머릿속에 입력이 되질 않고 끼워 맞추기 식으로 이해된 상태라 다음에 복습하는 시간도 가져야 될 것 같습니다.