GANPU: An Energy-Efficient Multi-DNN Training Processor for GANs With Speculative Dual-Sparsity Exploitation
Problems to solve
- GAN training에는 막대한 양의 computation이 필요하며, GAN model의 크기는 지속적으로 증가하는 추세이므로, resource-contrained platform에서는 가속되기 어렵다
- GAN의 network와 layer들의 operating characteristic이 다양하므로 core/bandwidth allocation optimization이 어렵다
How to solve
- Adaptive spatiotemporal workload multiplexing(ASTM)으로 high processor/externeal bandwidth utilization을 유지.
- Input-output sparse convolution(IOSC) architecture로 input/output의 zeros에 대해 불필요한 연산을 skip
- Exponent-only ReLU speculation(EORS) algorithm으로 inference 단계에서 convolution 연산을 수행하기 전에 output zeros의 위치를 예측.
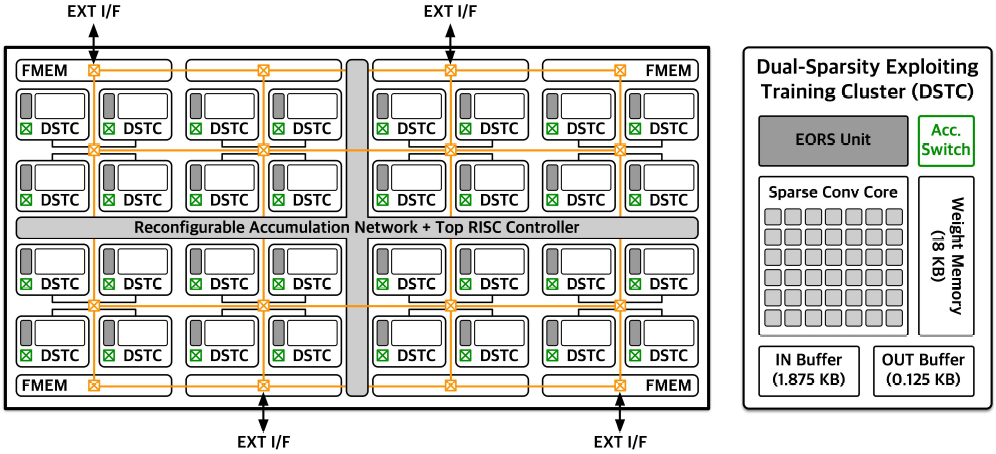
DSTC(Dual-Sparsity exploiting Training Core)
DSTC 내에는 6x7 크기의 PE array가 존재하며, 각 PE는 16b FP MAC 또는 2개의 8b FP MAC 연산을 지원한다.
MAC partial sum은 output buffer에서 accumulate되며, 각 DSTC의 partial sum은 RAN을 통해 accumulate된다.
EORS unit은 DSTC 내에 위치하여 연산 수행전에 output feature sparsity pattern을 분석한다.
Dual-sparsity exploitation
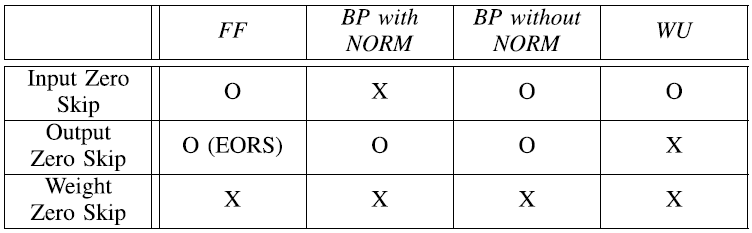
Throughput과 energy efficiency를 위해 PE는 input 또는 output이 zero인 경우 연산을 skip한다.
ASTM(Adaptive spatiotemporal Multiplexing)
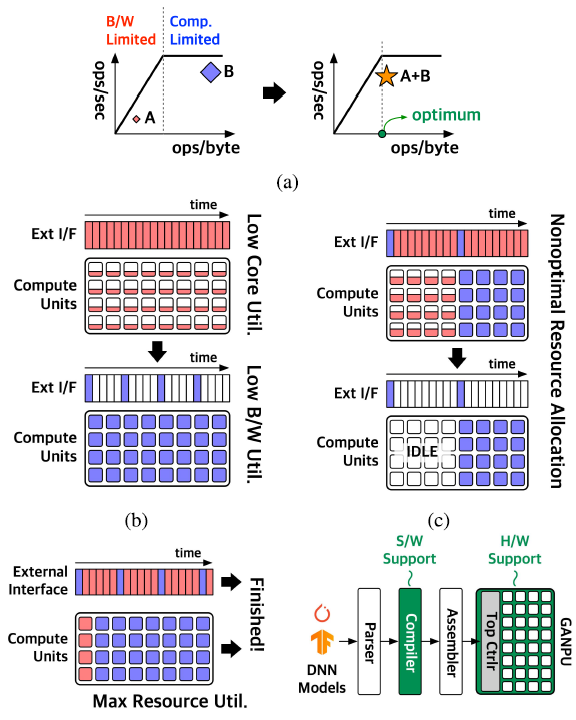
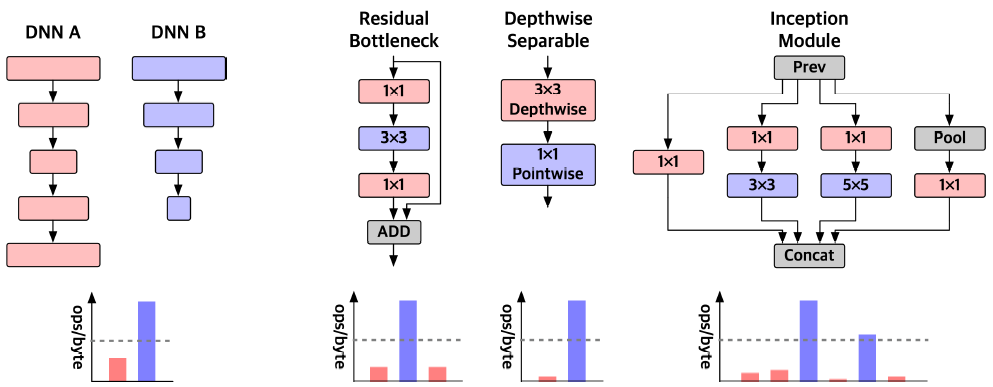
기존의 multiplexing 방식에는 temporal multiplexing(TM), spatial multiplexing(SM)이 있다. TM은 모든 core에 한가지의 workload만을 할당한다(b). 따라서 A의 경우 core utilization이 낮고, B의 경우 bandwidth utilization이 낮다.
SM은 여러 workload를 동시에 할당한다. 따라서 resource utilization은 TM에 비해 높지만, A의 수행이 먼저 끝날 경우 많은 core가 idle상태로 남아있는다. 따라서, fixed SM은 다양한 workload에 대해서는 비효율적이다.
ASTM은 다양한 workload에 대해 높은 resource utilization을 유지하기 위해 제안되었으며, external interface와 core들을 공유한 상태에서 여러 workload에 대해 latency를 최소화하도록 core mapping을 수행한다.
ASTM은 각 network 혹은 layer별로 적용 가능하다. Compiler는 runtime 이전에 모델의 종류, kernel size, stride, number of channel 등의 hyperparameter를 이용하여 scheduling을 수행한다. 이후 모델은 한개의 DSTC가 수행할 수 있는 단위인 unit tile 단위로 나뉘어진다.
RAN(Reconfigurable Accumulation Network)
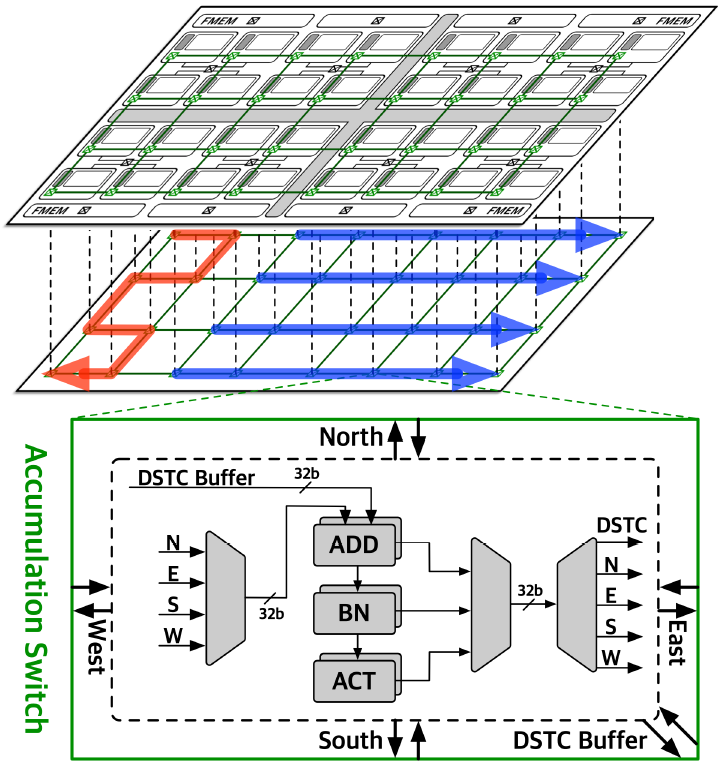
ASTM이 PE array의 division boundary를 dynamic하게 바꾸므로, partial sum accumulation도 dynamic하게 바뀌어야 한다.
DSTC내부의 accumulation switch는 RAN과 4방향으로 연결되어 있으며, configuration에 따라 연결 방향을 바꿀 수 있다. 또한, normalization과 non-linear activation 연산도 RAN에서 수행된다.
IOSC(Input-Output Sparse Convolution)
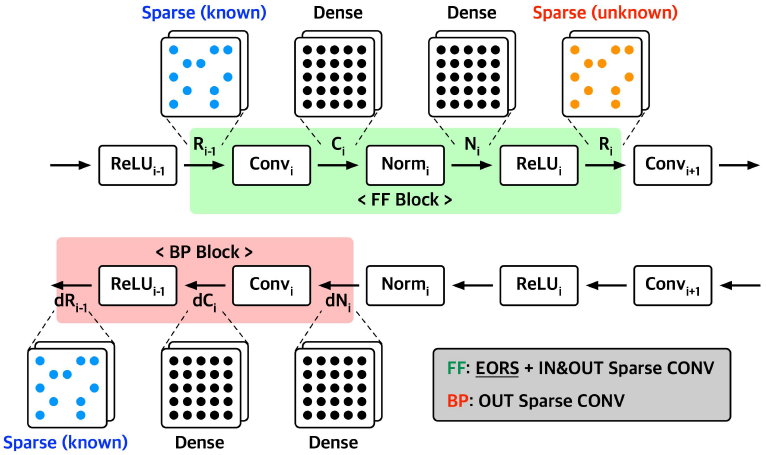
ReLU에 의한 feature map sparsity를 활용하면, 많은 양의 연산을 skip할 수 있다. 그러나 input sparsity pattern은 연산 수행전에 알 수 있는 반면, output sparsity pattern은 연산 후에 알 수 있다.
GANPU는 IOSC와 EORF를 통해 input/output sparsity를 모두 활용하는 dual-sparsity exploitation을 사용한다.
FF에서는 input/output sparsity를 모두 활용 가능하지만, BP에서는 normalization이 zeros를 없애므로 input sparsity를 활용할 수 없다. 그러나, output sparsity pattern은 FF 단계에서 정해지므로 output sparsity는 활용할 수 있다.
ISOC Core
ISOC를 지원하는 DSTC 내부의 PE는 아래 그림과 같이 구성되어있다.
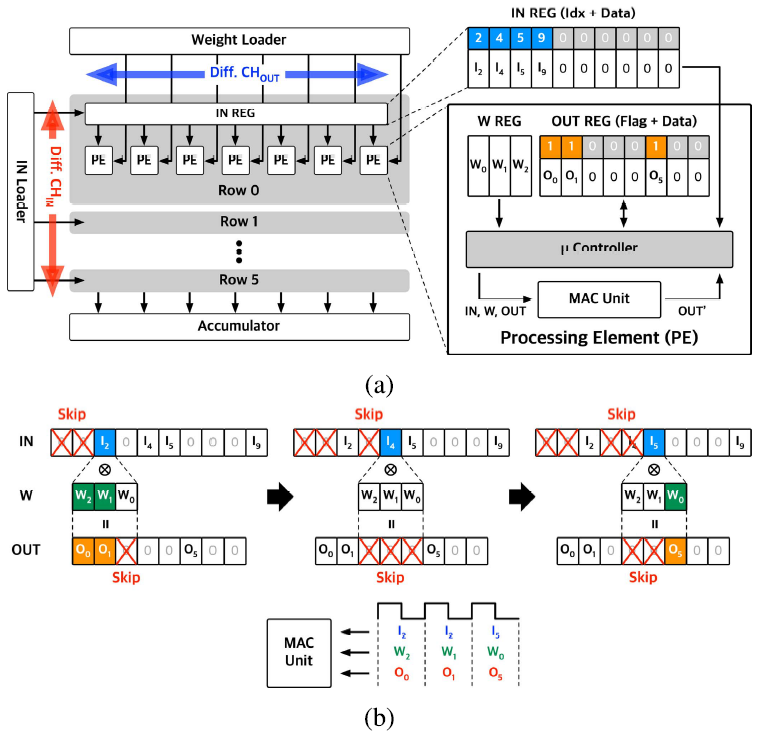
ISOC는 PE 내부의 microcontroller에 의해 control되며, input 또는 output이 zero인 경우 연산을 skip한다. 따라서 input과 output 모두 zero가 아닌 연산만을 골라야한다.
IN REG에는 input data와 non-zero index가 같이 저장되있고, OUT REG에는 non-zero flag가 저장되어있다. Microcontroller는 overlapping non-zero pattern을 분석하여 MAC 연산에 필요한 값들만을 fetch한다.
각 PE의 sparsity가 다르므로, 연산이 끝날때 까지의 latency도 모두 다르다. GANPU는 기존 LNPU에서 사용된 workload balancing technique를 사용하였다. PE가 연산을 끝내면, weight loader와 IN loader에 done flag를 보낸다. Done flag를 받으면, 미리 fetch 해놓은 다음 workload를 해당 PE에 할당한다.
추가적으로, DSTC의 controller는 output sparsity pattern을 분석하여 channel 연산 순서를 조정한다. 각 channel의 sparsity를 최대한 일치시켜 throughput을 증가시킨다.
Different types of convolution
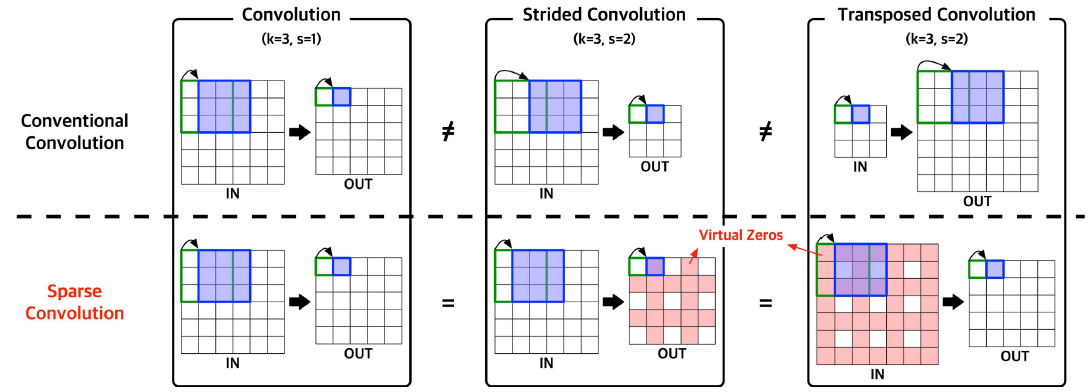
GAN의 경우 vanilla convolution, strided convolution, transposed convolution이 모두 사용된다. 기존 GAN accelerator는 transposed convolution을 지원하기 위한 overhead가 존재하였지만, GANPU는 ISOC architecture로 인해 모든 종류의 convolution을 지원한다.
Strided convolution은 output에 virtual zero가 존재하고, transposed convolution은 input에 virtual zero가 존재한다. ISOC는 input/output sparsity를 모두 활용하므로 hardware overhead 없이 이들을 모두 지원한다.
추가적으로, strided convolution과 transposed convolution은 각각 FF/BP 관계이므로 BP도 지원한다.
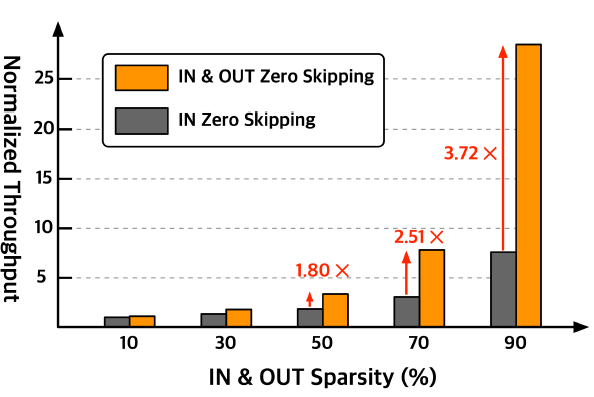
위 그림과 같이 input sparsity만을 활용할 때에 비해, output sparsity도 같이 활용하면 throughput이 상당히 향상된다.
EORS(Exponent-Only ReLU Speculation)
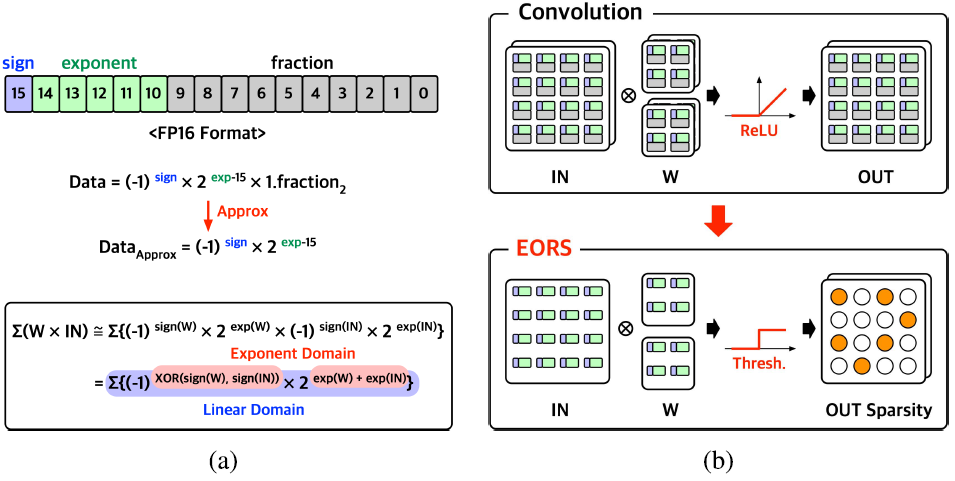
FF 단계에서 output sparsity를 활용하기 위해서는 output sparsity pattern을 알아야하지만, 이는 연산이 수행된 이후에야 알 수 있다.
EORS는 input과 weight의 exponent만을 이용해 approximate convolution을 수행하여 output sparsity pattern을 예측한다.
Floating point 연산은
와 같이 FXP 연산으로 approximate 된다. 따라서, 복잡한 floating point연산 대신 FXP 연산만으로 output sparsity pattern estimation을 수행한다.
FXP 연산 결과에 threshold value를 적용하여 output sparsity pattern을 예측하는데, 이 threshold는 layer-wise speculation error rate를 기반으로 EORS를 사용할 때와 사용하지 않을 때의 zero pattern을 반복적으로 비교하여 구해진다.
Speculation error rate는 hyperparameter로, 높을 경우 sparsity는 높아지지만 accuracy는 낮아진다.
ePE(exponent PE)
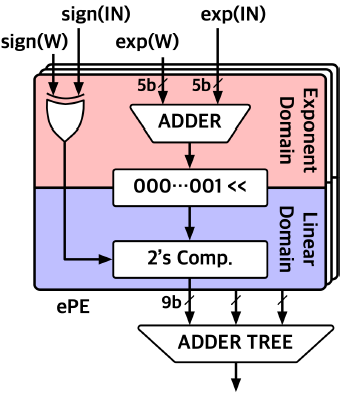
EORS 연산을 수행하는 ePE의 구조는 위와 같다.
EORS 연산의 latency를 hiding하기 위해, ePE와 IOSC core는 pipeline되어 연산이 수행된다.
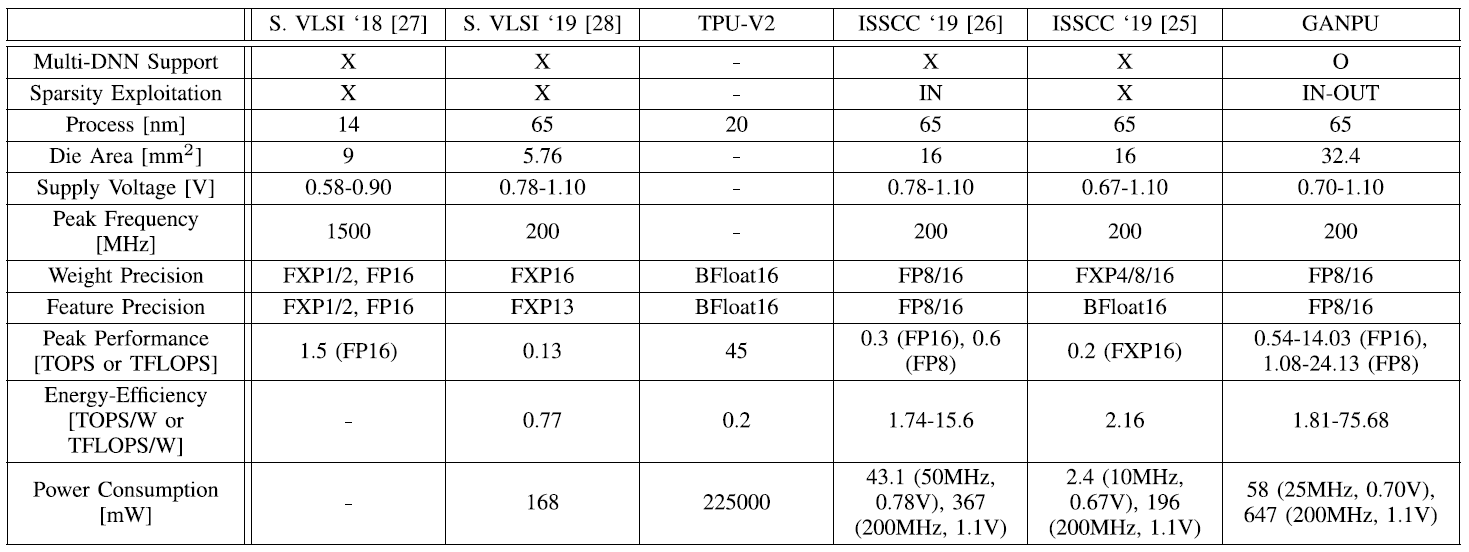
Comparison table