ISSCC'21

15.1

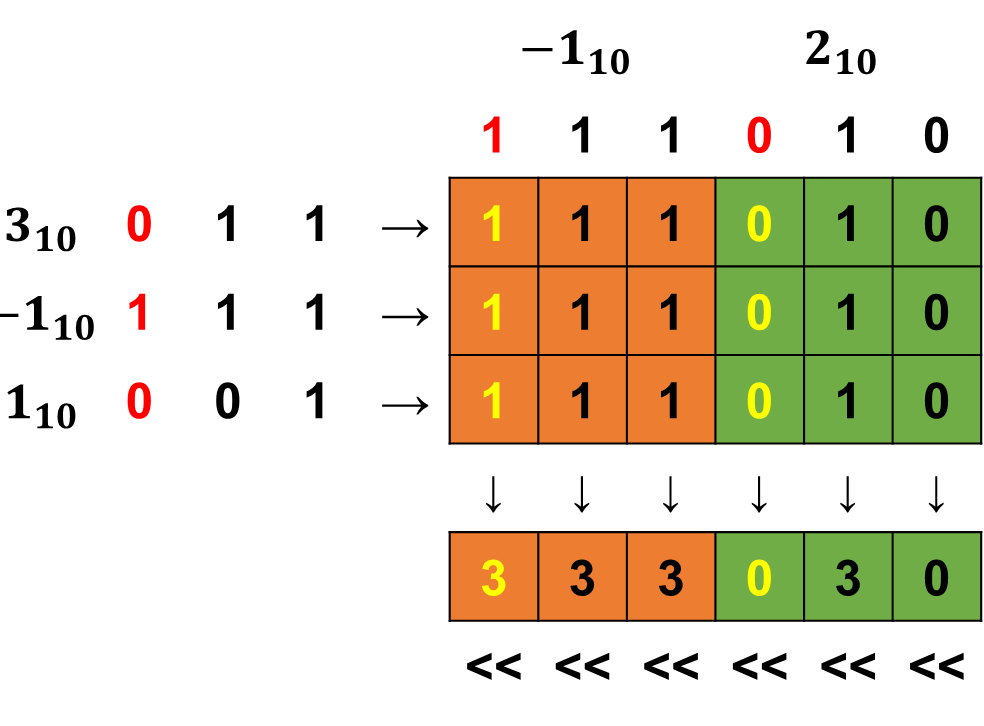
BPBS scheme을 사용하여 input/weight 모두 unsigned/signed 표현이 가능하다. 아래와 같이 각 weight의 MSB에 해당하는 column과, input의 MSB가 입력되는 cycle에 해당하는 결과값에 -1를 곱해주어 signed 연산을 수행한다.

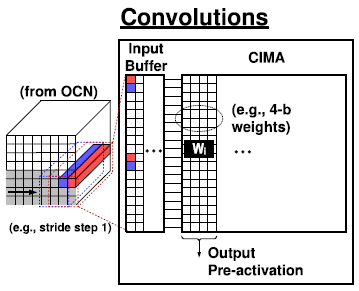
Convolution 연산 수행시 kernel은 flatten되어 CIMA 내부로 load되고, 해당하는 input이 channel-wise로 CIMA에 입력되는 것 같다. 이 경우 weight bit precision을 $B_W$, kernel size를 $K \times K$라 하면, 각 channel당 $K^2$개의 row와 $B_W$의 column을 차지할 것이다. CIMA는 1152x256 크기이므로, 3 X 3 크기의 kernel을 사용한다면 row-wise로 128 channel의 weight을 load할 수 있을 것이다.

Weight bit precision은 최대 8b이므로, column-wise로는 최소 32개의 weight를 load할 수 있다. 아마 다른 output channel을 구성하는 weight를 저장하고, input을 stride하여 CIMA에 입력할 것으로 예상된다.

15.2

PP-CIM은 각각 6T SRAM 4개로 구성된 A/B-BMU와, input과 weight간의 연산을 수행하는 LCC로 구성되어있다. Weight는 1b씩 6T SRAM에 저장되고, input은 GBL/GBL-B로 1b씩 입력되어 HGBL/HGBL-B을 통해 연산결과를 얻는다. 이를 통해 LCC는 2b의 input과 1b voltage로 표현되는 weight간에 연산을 수행하는 것 같다.

Input이 serial하게 입력되지 않고, column-wise로 parallel하게 입력될 것으로 추측되는데, input은 2b씩 연산되므로, MSB에 해당하는 연산값만을 따로 처리하는 것이 불가능해 signed input은 지원할 수 없을 것이다. Weight는 row별로 bit-parallel하게 저장되는데, weight의 MSB를 reatout할 때 연산값의 sign을 반전하여 accumulate함으로써 signed weight는 지원할 수 있을 것이다.

15.3

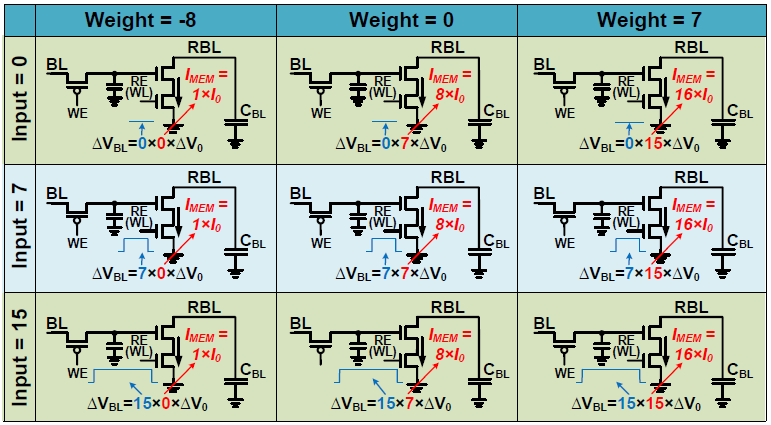
Weight는 cell 내부 capacitor의 4b voltage level로 표현되며, negative weight를 표현하기 위해 original value에 +8하여 저장된다([-8 ~ 7] $\to$ [0 ~ 15]). Input은 4b time pulse로 표현되며, input value에 비례하여 pulse의 width가 증가한다. Input은 ReLU를 통과한 값으로 생각하여 unsigned 형태인 것 같다.

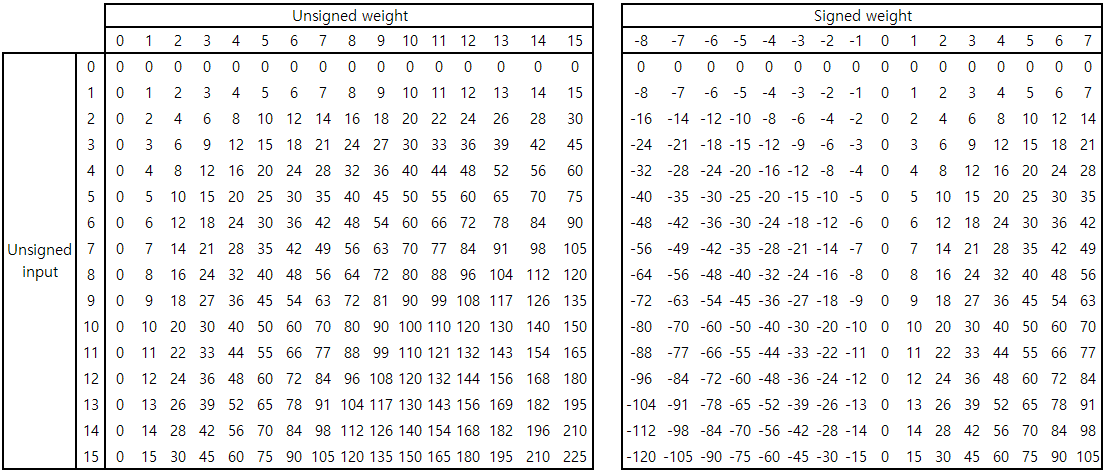
Unsigned input과 +8 shift된 unsigned weight/signed weight 간의 연산 결과는 위와 같다. 이 둘의 차이에서 확인할 수 있듯이, shift된 unsigned weight를 사용한 연산 결과는 signed weight를 사용한 연산 결과와 input에 비례하는 차이를 보인다. 따라서, 연산 결과에서 $8 \times Input$ 만큼 빼줌으로써 signed weight를 사용한 연산 결과를 얻을 수 있다.

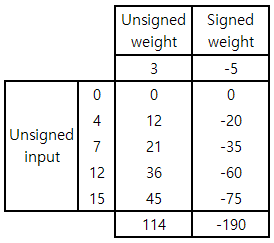
위와 같이 5개의 input과 1개의 weight간의 dot product를 계산하는 상황을 생각해보자. Unsigned weight을 사용한 연산 결과는 $3 \times (0+4+7+12+15)=114$이고, signed weight를 사용한 연산 결과는 $-5 \times (0+4+7+12+15)=-190$ 이다. 앞서 언급한 바와 같이 unsigned weight을 사용한 연산 결과에서 $8 \times \sum Input=8 \times 38=304$ 만큼 빼줌으로써 signed weight를 사용한 연산 결과를 구할 수 있다$(114-304=-190)$.

위의 예제와 같이 signed weight를 사용한 연산 결과로 복원하는 부분은 CIM macro 외부의 ASIC core에서 수행된다.

논문에서는 weight만 shift시켰지만, input 또한 shift 시킬 수 있다.

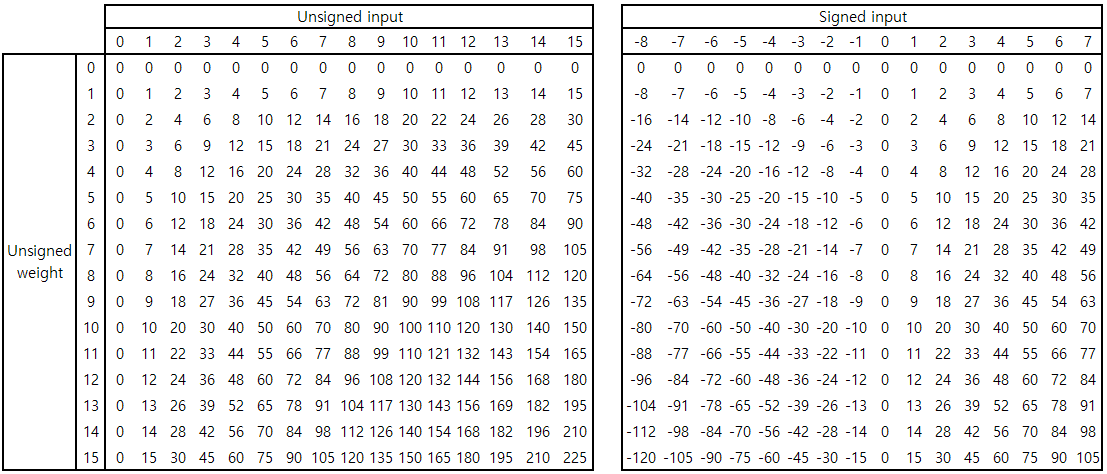
Input의 경우에도 앞선 weight의 경우와 유사한 경향성을 보인다. Hidden layer의 output의 경우 ReLU를 거친다는 가정하에 모두 0 이상의 값을 가지므로 다음 layer의 input은 unsigned형으로 표현이 가능하다. 그러나, input layer의 경우에는 input이 0 이상이지 않을 수도 있다. 이 경우에도 input이 +8 shift된 값이라고 가정하면, shift된 unsigned input을 사용한 연산 결과는 signed input을 사용한 연산 결과와 weight에 비례하는 차이를 보인다. 따라서, 연산 결과에 $8 \times Weight$ 만큼 빼줌으로써 signed input을 사용한 연산 결과를 얻을 수 있다.

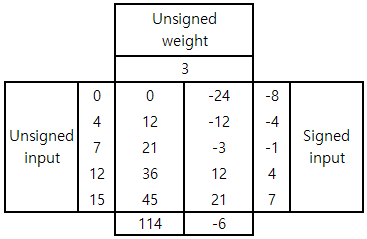
위와 같이 5개의 input과 1개의 weight간의 dot product를 계산하는 상황을 생각해보자. Unsigned input을 사용한 연산 결과는 $3 \times (0+4+7+12+15)=114$이고, signed input을 사용한 결과는 $3 \times ((-8)+(-4)+(-1)+4+7)=-6$이다. 앞서 언급한 바와 같이 unsigned input을 사용한 연산 결과에서 $5 \times (8 \times Weight)=5 \times 8 \times 3=120$ 만큼 빼줌으로써(Input이 5개 이므로) signed weight를 사용한 연산 결과를 구할 수 있다$(114-120=-6)$.

만약 input과 weight 모두 +8 shift된 unsigned 형태라고 가정하면, signed input/weight과의 차이는 위와 같다. 이 때의 차이는 input과 weight의 합에 비례하며, 연산 결과에 $8 \times (8 - (input + weight))$를 더해줌으로써 signed input/weight를 사용한 연산 결과를 얻을 수 있다.

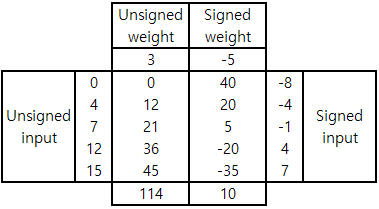
위와 같이 5개의 input과 1개의 weight간의 dot product를 계산하는 상황을 생각해보자. Unsigned input/weight을 사용한 연산 결과는 $3 \times (0+4+7+12+15)=114$이고, signed input/weight을 사용한 연산 결과는 $(-5) \times ((-8)+(-4)+(-1)+4+7=10$이다. 앞서 언급한 바와 같이 unsigned input/weight을 사용한 연산 결과에서 $8 \times \sum (8 - (input + weight))=8 \times (40-(3 \times 5+\sum Input))=8 \times (-13)=-104$ 를 더해줌으로써 signed input/weight를 사용한 연산 결과를 구할 수 있다$(114+(-104)=10)$.

15.4

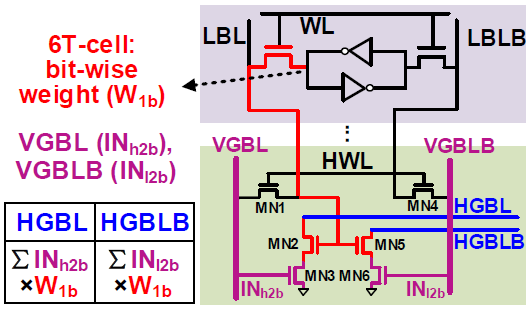
Weight는 6T SRAM에 1b씩 저장되며, 4b input은 LCC의 VGBL/VGBLB를 통해 각각 2b의 voltage로 표현된다. VGBL에는 상위 2b, VGBLB에는 하위 2b이 인가된다. 이를 통해 1 cycle에 4b input과 1b weight간의 연산을 수행한다.

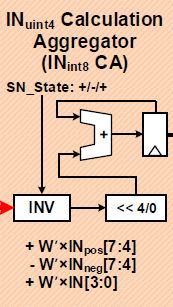
Input은 4b signed format인데, 2개의 4b unsigned value로 나뉘어져 두 값의 차이로 4b signed value를 표기한다. 예를 들어 -7은 $0-7$, 5는 $5-0$ 과 같이 표기한다. Neg. value의 경우 값을 누적하기 전에 sign을 바꾸어준다.

Weight는 1b씩 연산되므로, MSB에 해당하는 연산값은 누적할 때 sign을 바꾸어 줌으로써 signed weight는 지원할 수 있을 것이다.

ISSCC'20

14.3

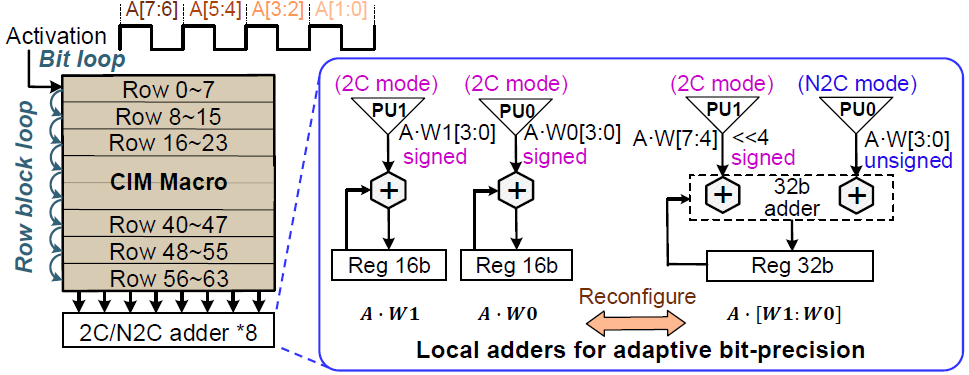
Weight는 8T SRAM에 1b씩 저장되며, input은 2b voltage level로 표현되어 입력된다. 기본 연산 단위인 SWB는 8 x 4 크기로, 4b signed weight를 지원한다. PU는 4 column의 연산값을 construct하며, 2C/N2C 둘다 지원하여 signed/unsigned weight 모두 지원한다. 2C mode의 경우, MSB에 해당하는 연산 결과는 sign을 반전하여 값을 누적할 것이다.

기본적으로는 signed mode로 작동하여 signed 4b weight에 대한 결과값을 construct하며, 8b signed weight일 경우에는 MSB쪽 PU는 2C, LSB쪽 PU는 N2C로 reconfigure하여 8b signed weight를 지원한다.

Input은 2b씩 연산되므로, MSB에 해당하는 연산값만을 따로 처리하는 것이 불가능해 signed input은 지원할 수 없을 것이다.

Mapping은 input channel의 수에 따라 channel-order/kernel-order mapping 중에 선택되며, compiler에 의해 strategy가 결정된다.

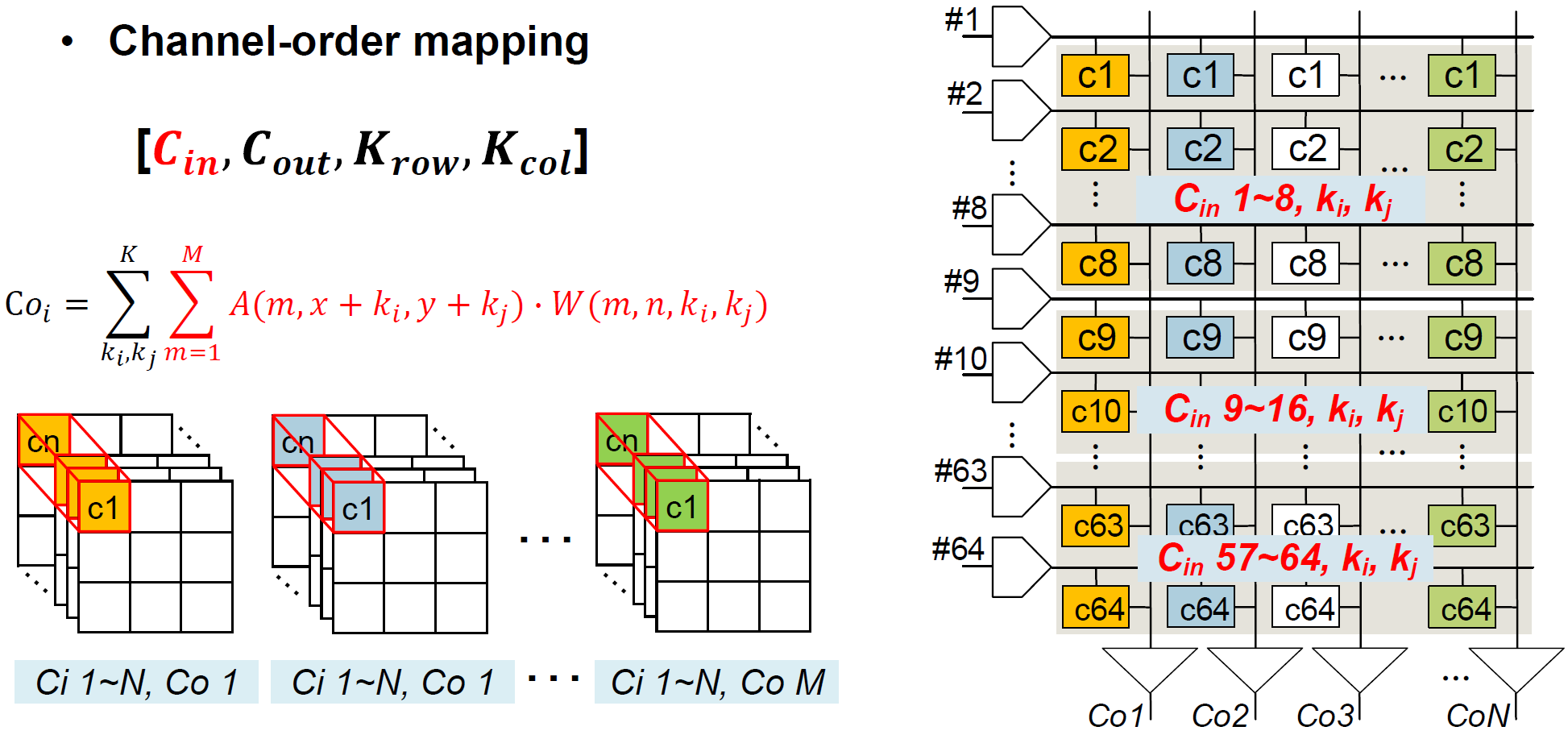
Input channel이 8개 이상인 경우, channel-order mapping을 사용한다. 64개의 column이 존재하고, 3 x 3 kernel을 사용할 경우, input channel별 weight는 9개이어서 $64 // 9 = 7$이므로, mapping의 기준 input channel은 8개이다. Weight는 row-wise로 input channel별, column-wise로 output-channel별로 저장된다. 따라서, column별로 output channel-wise partial sum이 구해지고, 다음 timestep에서 $i, j$를 변화시키며 spatial-wise로 partial sum을 누적할 것이다.

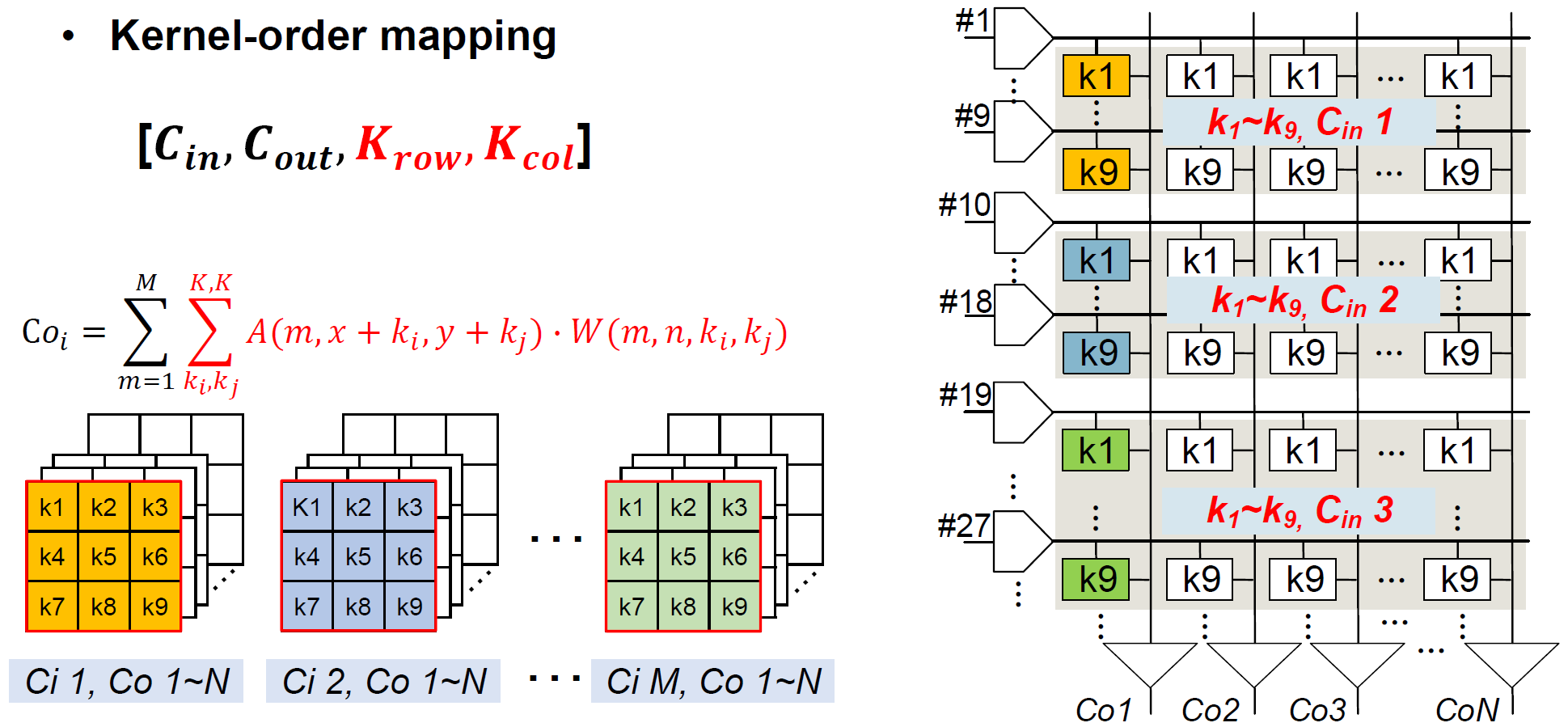
Input channel이 8개 미만인 경우, kernel-order mapping을 사용한다. 3 x 3 kernel을 사용할 경우, weight는 row-wise로 input channel별 9개씩, column-wise로 output-channel별로 저장된다. Kernel-order mapping의 경우에도 column별로 output channel-wise partial sum이 구해진다.

15.2

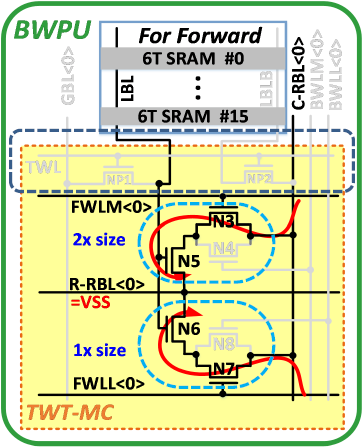
Weight는 6T SRAM에 1b씩 저장되며, input은 2개의 BL을 통해 입력된다. Input중 상위 bit인 IN[1]에 연결된 트랜지스터 size는 하위 bit인 IN[0]에 연결된 트랜지스터 size의 2배이다. 따라서, RBL의 output에는 weighted current가 흐르게 된다.

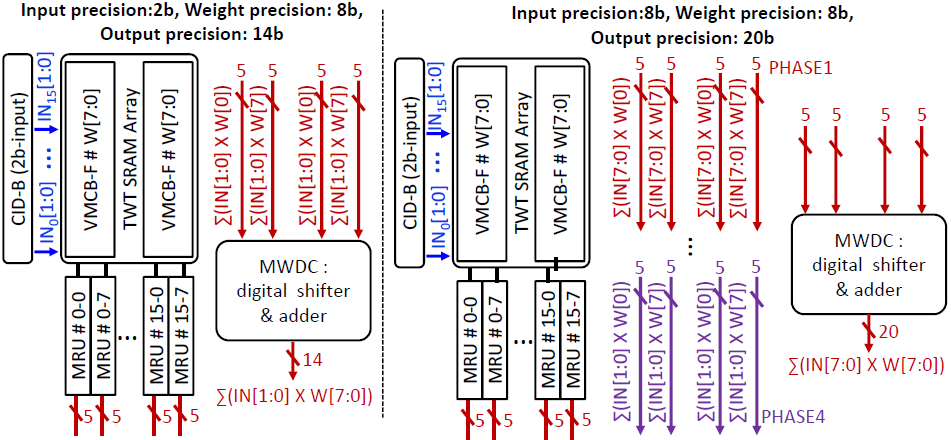
MWDC(Multi-bit Weight Digital Combiner)는 8 column의 연산결과들을 모아 output을 construct한다. 이때 W[0]에 해당하는 column의 결과값에 -1을 곱해 값을 construct 하면 signed weight를 지원할 수 있다. 4b signed input의 경우, W[0]과 W[4]에 해당하는 column의 결과값에 각각 -1을 곱하여 signed weight를 지원할 수 있다.

Input의 경우에는 2b씩 weighted current를 발생시키므로, unsigned format으로 추측된다.

15.3

4b input은 4b pulse로 나타내지며 input값에 비례하여 pulse의 갯수가 증가한다. ISSCC'21 15.3 논문도 input이 pulse로 나타내어 지는데, 이 논문은 input에 비례하여 pulse의 폭이 증가하지만, 이 논문은 pulse의 폭은 일정하고 pulse의 갯수로 input을 나타낸다. 따라서, unsigned input만을 지원하는 것으로 추측된다.

Weight는 8T SRAM에 1b씩 저장된다. Weight는 4b로 고정이며, 4b weight에 대한 output을 construct하기 위해 4 column의 output을 charge-sharing을 통해 weighted-sum을 한다. Charge-sharing을 사용하기에 unsigned weight로 추측되며, ISSCC'21 15.3 논문과 같이 signed weight에 +8 만큼 shift한 것으로 생각할 수도 있다.

15.5

이 논문의 bit multiplication과 multi-bit output construction 방식은 ISSCC'20 15.2 논문과 매우 유사하다.

Weight는 6T SRAM에 1b씩 저장되며, 4b input은 LCC의 VGBL/VGBLB를 통해 각각 2b의 voltage로 표현된다. VGBL에는 상위 2b, VGBLB에는 하위 2b이 인가된다. 이를 통해 1 cycle에 4b input과 1b weight간의 연산을 수행한다. 8b input에 대해서는 posedge clk에 상위 4b, negedge clk에 하위 4b이 입력되어 2 phase로 연산을 수행한다.

Input이 2b씩 인가되기 때문에, MSB에 해당하는 연산값만을 따로 처리하는 것이 불가능해 input은 unsigned format으로 추측된다.

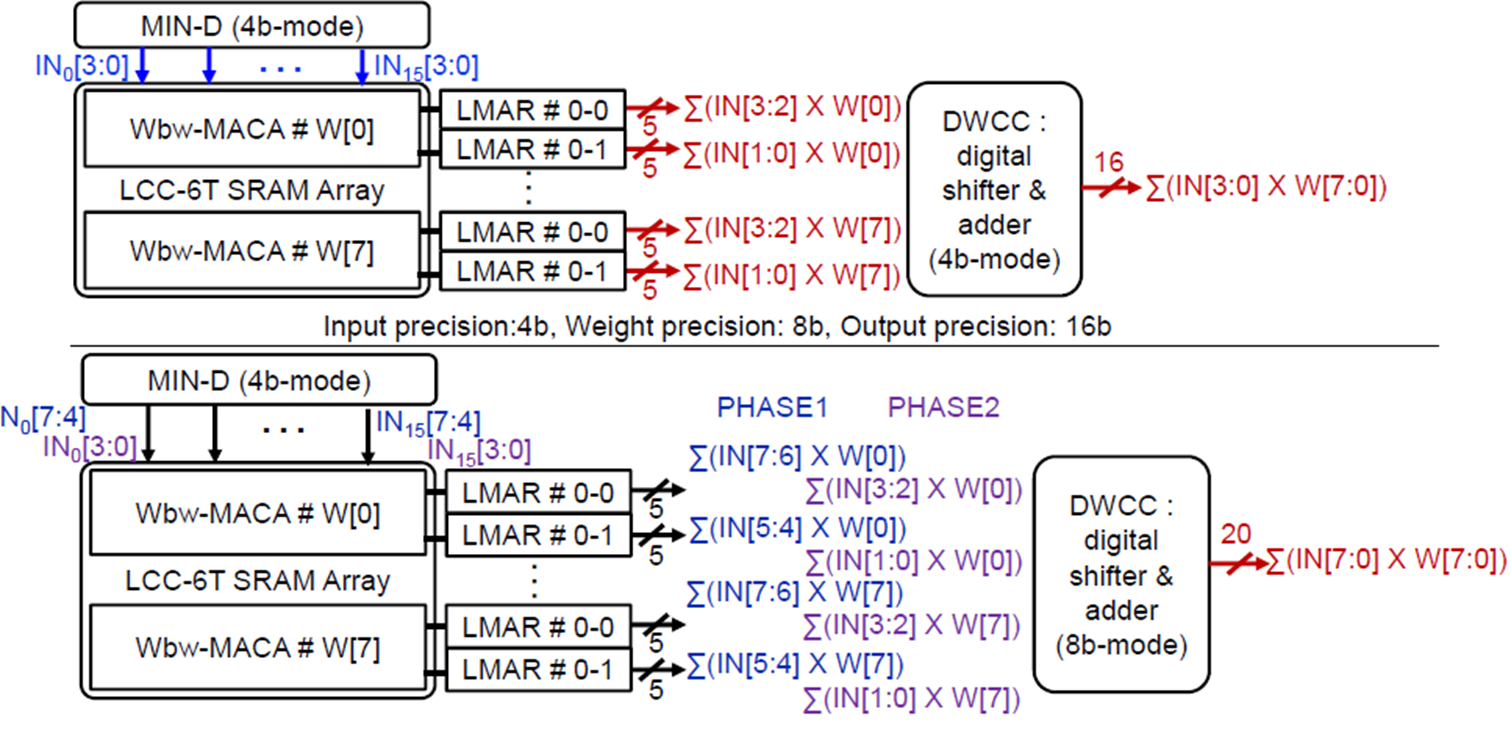
DWCC(Digital Weight Configuration Circuit)는 8 row의 연산결과들을 모아 output을 construct한다. 이때 W[0]에 해당하는 row의 결과값에 -1을 곱해 값을 construct 하면 signed weight를 지원할 수 있다. 4b signed input의 경우, W[0]과 W[4]에 해당하는 row의 결과값에 각각 -1을 곱하여 signed weight를 지원할 수 있다. DWCC 또한 input의 bit-precision에 따라 8b mode에서는 1 cycle안에 2 phase로 동작한다.

VLSI'21

JFS 2-2

Weight는 10T SRAM에 1b씩 저장된다. Input/weight는 모두 1b 또는 2b 이며, input은 1b씩 LSB부터 CIM macro에 입력된다. 2b input/weight를 지원하는 원리는 ISSCC'21 15.1 논문의 BPBS와 유사하다. ADD2$(Z=2X+Y)$ SIMD 연산을 통해 2b input/weight를 지원한다. 그러나 sign을 반전하는 연산이 없는 것으로 보아 input/weight 모두 unsigned format으로 추측된다.

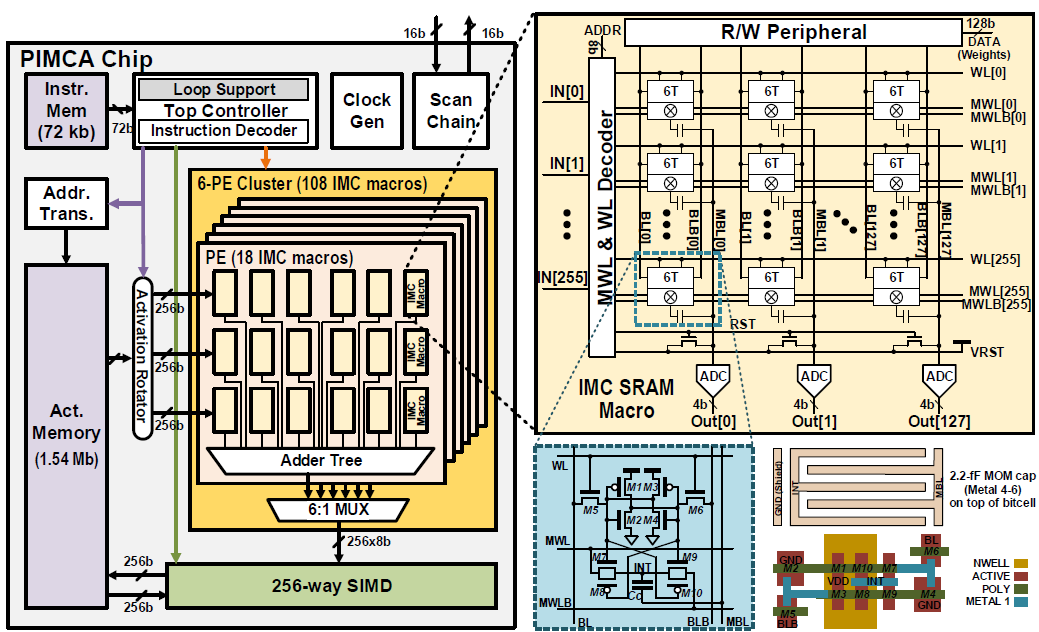
PIMCA는 256 x 128 크기의 IMC macro가 3 x 6 으로 배열된 PE가 6개 존재한다. PIMCA는 3 x 3 kernel의 convolution에 맞추어 설계되었으며, 각 PE당 256 channel의 1b convolution 혹은 128 channel의 2b convolution을 수행한다. 각 PE는 channel-wise로 weight를 저장하며, 각 PE에 저장된 weight의 spatial location은 같다. 따라서 1 x 1 크기 이상의 kernel을 위해서 여러개의 PE가 사용되며, 해당하는 input은 row에 대해서는 parallel하게, column에 대해서는 serial하게 pipelining 되어 입력된다.

1b weight의 경우, PE는 128개의 column을 가지므로, 128 channel에 대한 weight를 column-wise로 저장한다. Row는 256개 이므로, 256 channel에 대한 input이 row-wise로 입력된다. 3 x 6 크기의 PE는 kernel이 3 x 3 크기이므로, 3 x 3 크기로 좌우 2개의 group으로 나뉜다. 각 group이 128 channel에 대한 연산을 수행하여 총 256 channel에 대한 연산을 수행할 수 있다.

2b weight의 경우, 왼쪽 group에는 weight의 MSB가, 오른쪽 group에는 weight의 LSB가 저장된다. 이 경우, 두 group은 같은 weight를 저장하고 있지 않아 128 channel에 대한 연산만을 수행할 수 있다. 두 group의 output에 앞서 언급한 ADD2 연산을 수행하여 2b weight에 대한 output을 construct한다.

1b FC도 위와 같이 지원한다. Convolution의 경우 각 PE에 channel-wise로 같은 spatial location의 weight를 저장했지만, FC의 경우 각 PE에 256 input channel과 128 output channel에 대한 weight를 저장한다. 각 group은 128 channel output에 대한 연산을 수행하므로, 각 group에 동일한 input을 입력하여 256 channel output에 대한 연산을 수행할 수 있다. 각 PE에는 256 input channel에 대한 weight가 저장되고, 각 group은 9개의 PE로 구성되어 있으므로, $256 \times 9=2304$의 input channel에 대한 연산을 수행할 수 있다. 즉, 2304 x 256의 1b FC 연산을 수행할 수 있다. 필요에 따라서 4608 x 128의 1b FC 연산도 수행 가능하다.

위와 같이 5 x 5 kernel의 convolution이나, zero-padding 또한 PE를 deactivate하여 지원한다. 5 x 5 kernel convolution의 경우, 한 group 안에 weight가 모두 저장되지 않아 128 output channel에 대한 연산을 수행하며, PE array가 3 row이므로 PE 1개에 2개의 spatial location에 대한 weight를 저장하여 128 input channel에 대한 연산을 수행한다.

JFS 2-4

Input은 5b로 고정이고, weight은 1b로 고정이다. Weight는 10T SRAM에 저장되며, 5b input은 DAC를 통해 5b voltage로 입력된다. 5b input의 MSB는 sign bit으로, 실질적으로는 4b 데이터이기에 16 level의 DRD(Dynamic-Range Doubling)-DAC를 사용한다. DRD-DAC를 사용함으로써 5b signed weight를 지원한다.

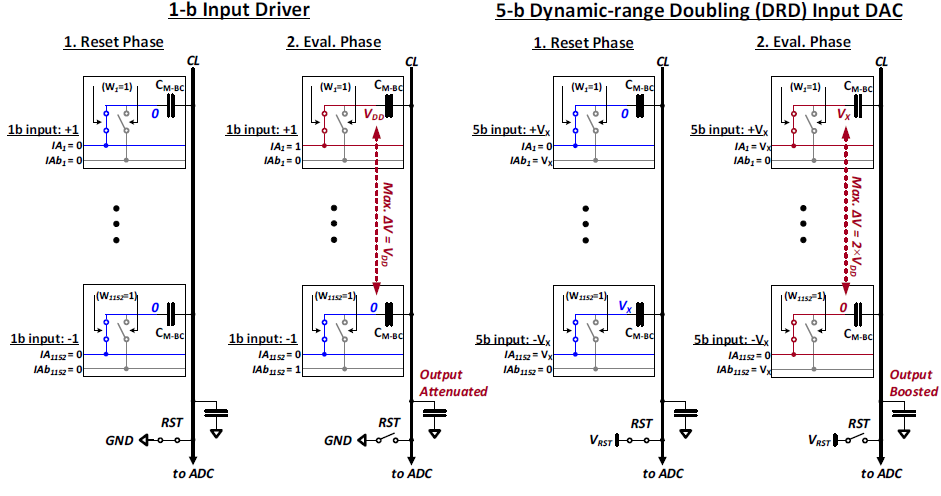
기존의 capacitor-based IMC는 reset phase에서 IA와 IAb 모두 GND로 설정한 후, evaluation phase에서 input에 맞게 둘 중 하나를 VDD로 설정하여 bit-wise multiplication을 수행한다. 이는 CL에 charge re-distribution을 일으키고, CL의 voltage drop을 ADC를 통해 변환하여 output을 얻는다. 이 경우, CL의 voltage dynamic range는 VDD이다.

DRD-DAC는 reset phase에 IA/IAb를 GND로 설정하는 대신, input의 sign에 따라 IA 혹은 IAb를 input의 절댓값으로 설정하고, 나머지를 GND로 설정한다($V_X>0$에 대해, $Input=V_X$이면 IA=GND, IAb=$V_X$, $Input=-V_X$이면 IA=$V_X$, IAb=GND). 또한 기존에는 CL을 GND로 reset하지만, CL을 $V_{RST}$으로 reset하는데, $V_{RST}=V_{DD}/2$으로 생각된다. Evaluation phase에서는 IA와 IAb의 값을 서로 바꾸어주며, 이로 인해 CL에 charge re-distribution이 발생한다. Reset phase에서 $V_{RST}=V_{DD}/2$으로 설정함으로써 $V_{RST}=V_{DD}/2$만큼 shift된 output을 얻는다. 이 경우, M-BC의 연산 과정은 기존과 동일하지만 CL의 voltage dynamic range는 2VDD로, 기존 방식에 비해 2배이다.

VLSI'20

CM 3.4

기존 CIM들이 weight를 CIM에 저장하고 input을 입력하는데 반면, Z-PIM은 input을 CIM에 저장하고 weight를 입력한다. Input은 16b 고정이고, weight는 1-16b를 지원한다.

Z-PIM 또한 ISSCC'21 15.1의 BPBS scheme과 유사하게 multi-bit IMC를 지원한다. 논문 상에는 input/weight가 signed라고 언급되어 있지는 않지만, 지원하지 않는다 하더라도 BPBS와 유사하게 signed input/weight를 지원할 수 있을 것이다.

Convolution을 위한 dataflow는 다음 3단계로 나뉜다.

1. Channel-wise accumulation

ZC-SRAM은 256x128 크기이므로, 8개의 16b input$(i_0 \sim i_7)$이 row-wise로 channel 별로 저장된다(row0에는 channel[0], row1에는 channel[1]). 이후 row-wise로 weight가 1b씩 pre-charge되어 and 연산을 수행한다. 연산결과는 8개의 24b accumulator에서 input 별로 누적되고, 모든 channel에 대해 accumulation이 끝나면 연산 결과는 DA-SRAM으로 이동한다. Channel-wise accumulation이 끝나면 256-channel 16b 8-input과 1b weight의 곱의 partial sum$(\sum_{ch=0}^{255} {i_{0, ch} \& w_{k, ch}}[n])$이 구해진다.

2. Bit-wise accumulation

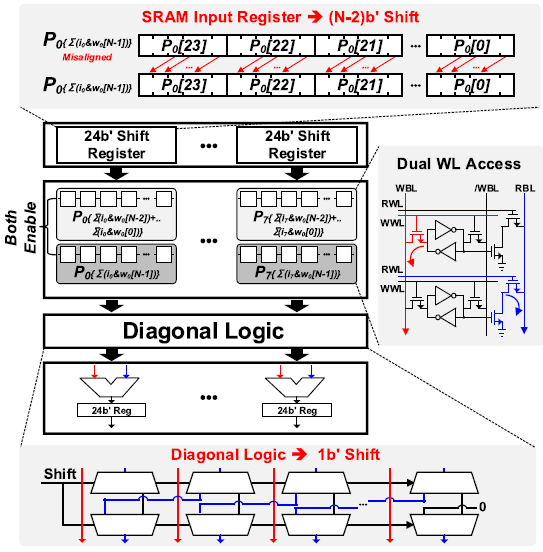
Bit-wise accumulation은 DA-SRAM에서 수행된다. 8개의 16b input이 weight의 1b씩 곱해져 partial sum을 이루었으므로, partial sum을 shift하여 weight의 bit-position을 맞추어 partial sum끼리 값을 더한다. 만약 weight가 16b이면 16개의 partial sum들의 합을 구한다. Bit position을 맞추기 위해 SRAM input register가 ZC-SRAM으로부터의 input을 shift하여 DA-SRAM에 저장시킨다.

DA-SRAM은 WBL과 RBL을 통해 동시에 2 row의 값을 읽을 수 있다. DA-SRAM의 한 row에는 partial sum이 저장되며, 이 row와 다음에 연산할 row를 동시에 enable 시켜 partial sum을 구한 후 결과값을 다시 DA-SRAM에 저장한다. Weight의 bit-precision만큼 partial sum accumulation을 반복하면 되므로, weight는 1-16b의 arbitary bit-precision를 가질 수 있다. Bit-wise accumulation이 끝나면 256-channel 16b 8-input과 16b weight의 곱의 partial sum$(\sum_{n=0}^{N} \sum_{ch=0}^{255} {i_{0, ch} \& w_{k, ch}}[n])$이 구해진다.

3. Spatial-wise accumulation

Bit-wise accumulation을 통해 하나의 weight에 대한 partial sum이 구해지며, 다른 weight들에 대한 partial sum들 간의 합을 통해 convolution output$(\sum_{k=0}^K \sum_{n=0}^{N} \sum_{ch=0}^{255} {i_{0, ch} \& w_{k, ch}}[n])$을 구한다. 이는 Z-PIM core가 아닌 top controller에 의해 수행된다.