"모두를 위한 열린 강좌 KOCW"에서 제공하는 한양대학교 이상화 교수님의 선형대수 수업을 정리한 내용입니다.
Chapter 3. Orthogonality
3.1 orthogonal vectors & subspace
vector 그리고 vector로 이루어진 space, 그 중 subspace 해당하는 부분이 수직일 수 있다. 그것을 살펴본다.
Why orthogonal vectors?
vector가 수직일 때 여러가지 장점이 있다.
1. independant basis vector로 이루어져 있다.
2. easy calculation in linear combination.
Length
- length of vector ||X||
vector 크기(길이)에 대한 제곱은 같은 vector를 transpose해서 곱하면 된다. 이는 vector의 각 element를 (n차원일 때) 제곱해서 더 한 것들이다.
벡터의 길이를 정의하면 직교하는 형태의 벡터들도 특별한 조건을 갖는 것을 정의할 수 있다.
Orthogonal

- for vector inner product
1)
2)
3)
If non-zero vectors are orthogonal,
then, the vectors are linearly independent!!
(Review!! linearly indep 하다는 얘기는
를 의미한다.)
따라서 각 계수가 모두 0이 되는지를 확인하면 linear indep하다는 것을 증명할 수 있다.
먼저 linearly independent combination 식에 임의의 i번째 orthogonal vector 를 inner product 해준다.
따라서 linearly indep한 vector 집합을 orthogonal한 basis vector로 구할 수 있다.
(Reviw!! basis vectors가 되면 vector space를 span한다고 했는데,
특정한 벡터공간 X를 표현하는데, basis vector를 가지고 linear combination해서 얻어내는 것이다. 즉, X라는 임의의 벡터가 orthogonal한 벡터를 가지고 span해서 만들어진다.
이때 는 양변에 를 내적해 구해준다.
만약 orthogonal vector의 크기(혹은 길이) ()가 1이 되도록 만들어주면 (othonormal, =1),
가 된다.
Orthogonal의 의미
linearly independent vector,
가 있다. 이 벡터를 가지고 n차원 벡터공간을 span할 수 있다. 그럼 특정한 벡터 X를 구할 때,
계수를 가지고 linear combination 할텐데 orthogonal하지 않으면 계수 는 연립방정식을 풀어 구해야 한다.
matrix a가 linear indep하니까 inverse를 구하던가 GE를 통해서 C를 구할 수 있을 것이다.
이때, 만약 orthogonal 하면 이렇게 귀찮고 번거로운 과정없이 orthogonal vector와 곱해 쉽게 C를 구할 수 있다.
Orthogonal Subspaces
이번에는 벡터가 아닌 벡터공간이 서로 수직인 경우에 대해 다뤄본다.
Every vector in one subspace is orthogonal to every vector in the other subspace
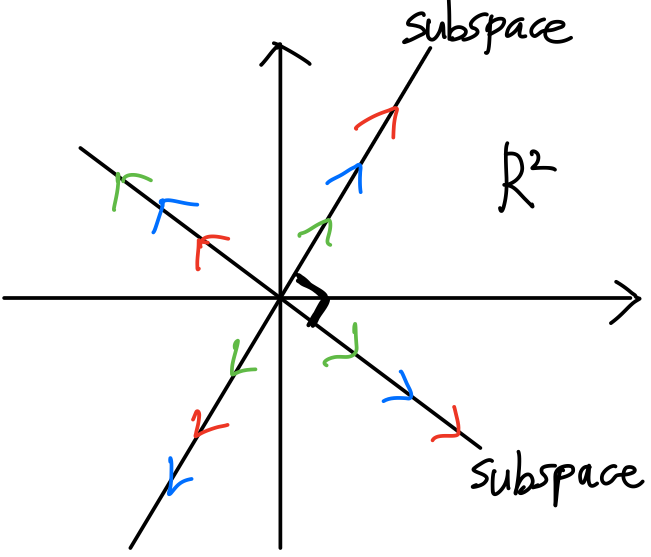
직선 위 모든 벡터는 vector space를 이루는데, 그 직선에 수직인 직선이 있다고 하자. 그 직선 위의 모든 벡터 또한 vector space를 이루고 이 두 vector space(subspace)는 서로 orthogonal하다.
3차원 공간은 어떨까?
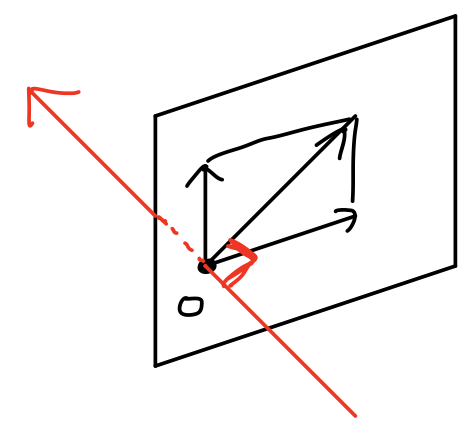
평면 상의 원점을 지나는 모든 벡터는 vector space를 이루고, 그 원점을 지나고 평면과 수직으로 관통하는 직선 위의 벡터 또한 vector space를 이룬다. 이 두개의 vector space(subspace)는 서로 orthogonal하다.
Row Space Null space
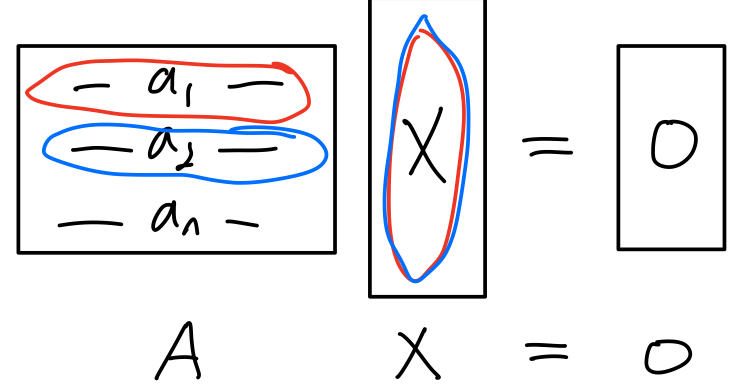
위의 연립방정식을 만족하는 X가 Null space solution이고, Row space는 행렬A의 행벡터의 linear combination이다. A의 row vector와 X를 곱하면 0이 나오므로 서로 수직이다. 즉,
Colum spaceLeft Null space
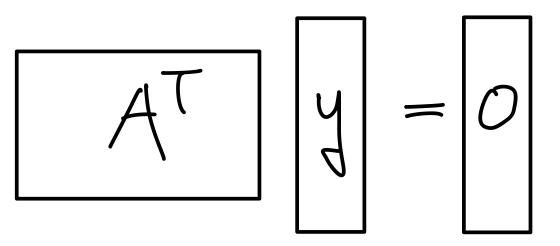
y는 Left Null space에 해당하는 solution이고, Column space는 행렬A의 column vector이다. 그것의 Transpose니까 row vector이다. 이때 위와 같이 row vector와 y는 서로 수직이다. 따라서 Column space와 Left Null space는 서로 수직관계가 된다.
조건
위의 Subspacee들이 서로 수직인데 아무렇게나 수직이 아니다.
행렬A가 m*n 일 때,
이다. 즉 vector dimension 모양이 다르다.
이때 Deimension은 vector space를 표현할 수 있는 independent한 vector의 개수가 몇개냐를 나타낸다.
Dim of Vector Space = # of indep vector to span the Vector Space
이것을 행렬로 생각하면 rank of A (r)이다.
즉,
예를들어, 3차원 공간에 vector space가 있다. 만약 Column Space가 직선이면 표현할 수 있는 기본 벡터는 하나면 되니까 1차원이다. 나머지 Column vector에 대응되는 Left Null Space에 해당하는 차원은 2차원이 되어야 하고 평면이다.
반대로, 3차원 공간에서 Row Space가 어떤 평면이면, 그것에 대응되는 Null Space는 원점을 지나는 어떤 하나의 직선이고 평면과 수직일 것이다.
그래서 3차원 공간 상의 직선과 수직인 직선이 있다면, 그것은 fundamental Subspace에서 서로 보안관계를 갖지 못한다. 직선이 있다면 적어도 평면이 있어야한다. 차원이 각각 1차원이기 때문이다.
이러한 관계를 Orthogonal Complement Subspace이라 한다.
Orthogonal Complement Subspace
이때 하필이면
두개의 vector는 서로 Orthogonal Complemnet Subpace 관계라고 한다.
3.2 Cosines and Projection onto line
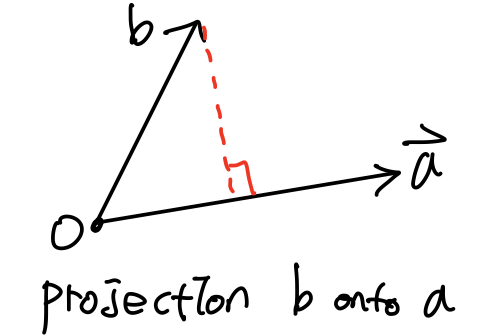
투영 Projection은 수선의 발을 구하는 것으로, 수선의 발 좌표를 구한다는 것은 b라는 점에서 직선 a상의 점 중 거리가 가장 minimum이 되는 점을 구하는 것이다.
Projection 이야기를 하기전에 벡터의 내적과 관련해서 cos에 대해서 정의하면,
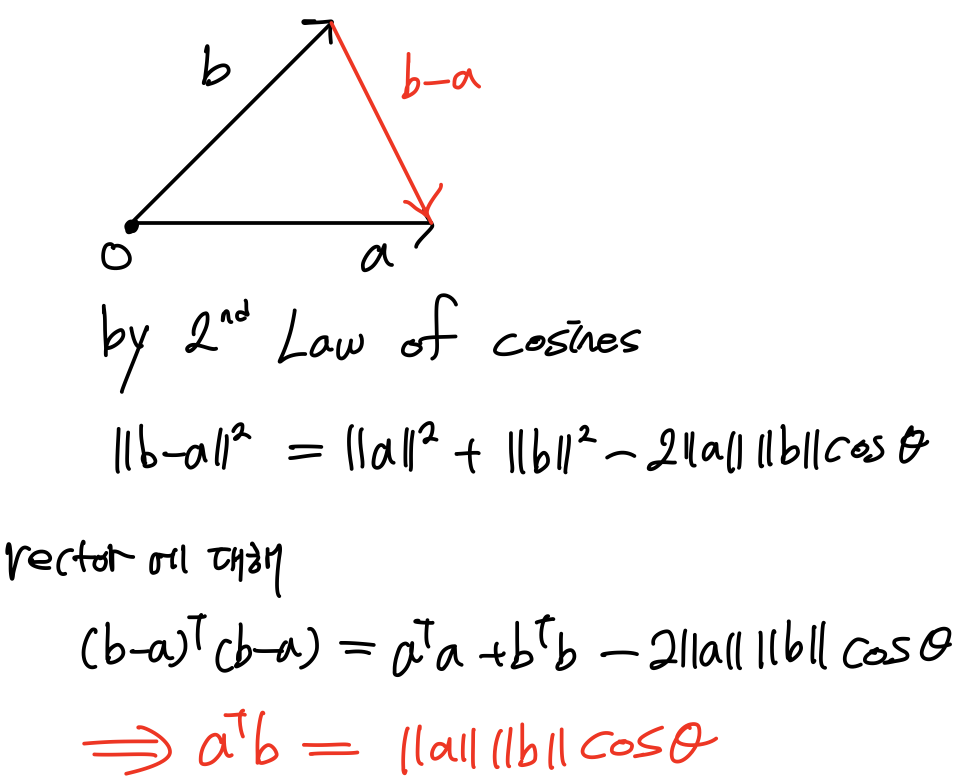
길이에 관련한 cos 제2법칙으로부터 두 개의 벡터에 대한 내적을 정의할 수 있다. 따라서 두 개의 벡터를 내적하는 것은 Projection을 구하는 것과 같다.
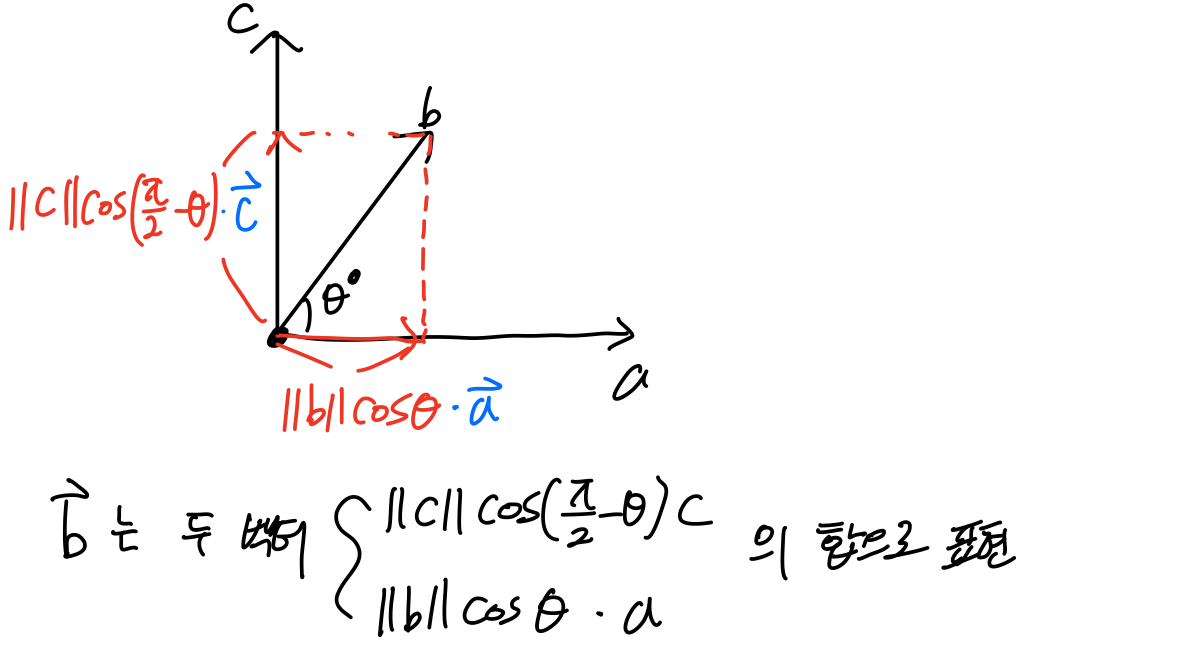
자, 다시 돌아가면
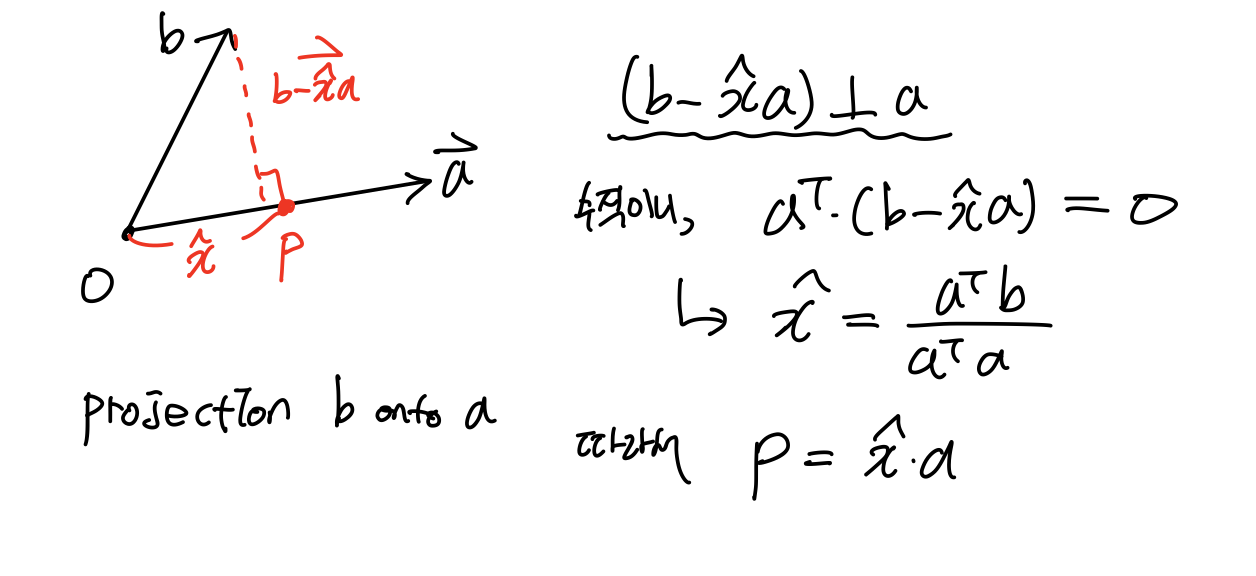
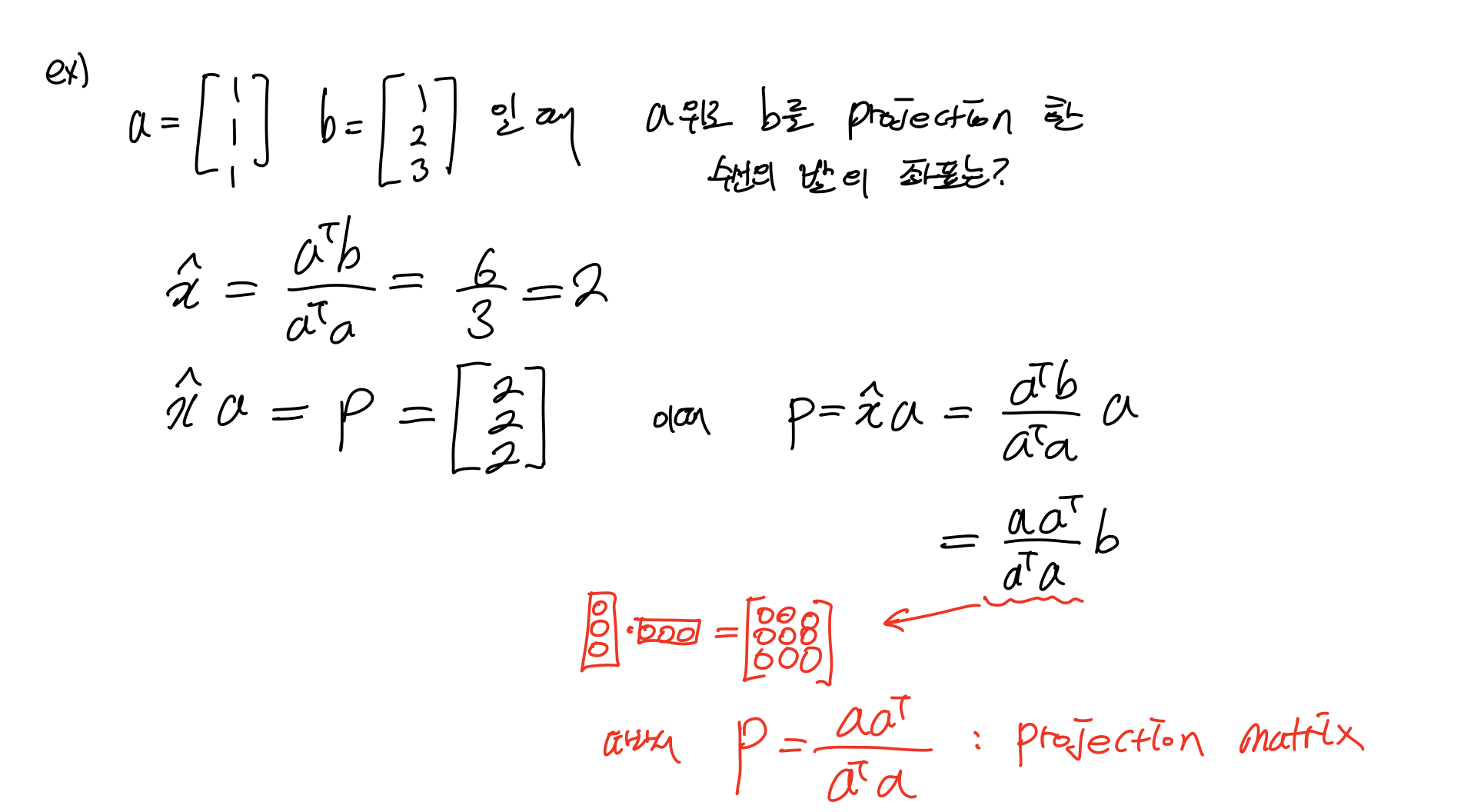
Projection mat은 또다른 특징이 있다.
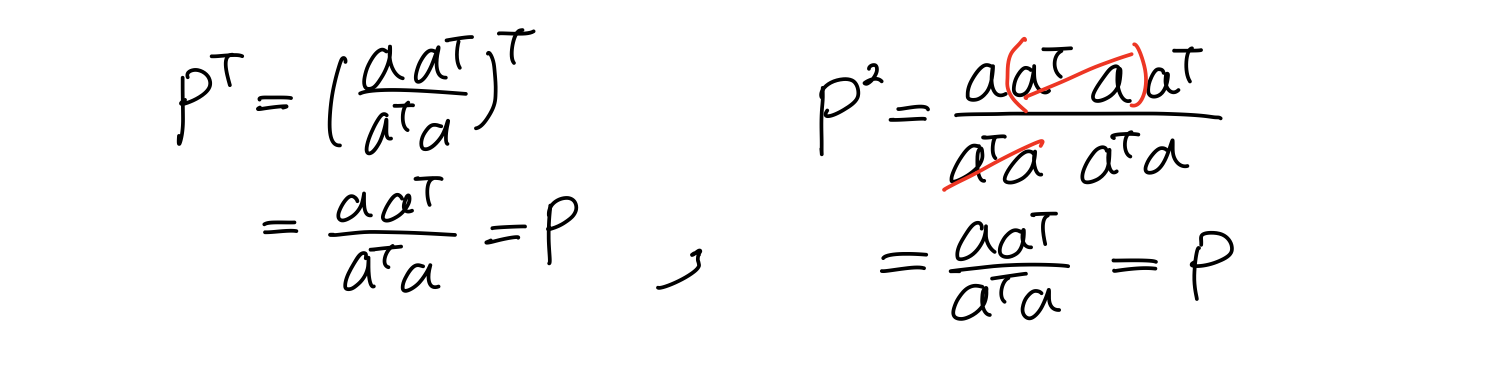
공간 상의 한점을 평면에 투영해서 얻은 수선의 발을 다시 투영한다고 바뀌지 않는다. 수학적으로 이라는 연산은 Projection이라고 한다. 도형적인 의미는 같다.
