"모두를 위한 열린 강좌 KOCW"에서 제공하는 한양대학교 이상화 교수님의 선형대수 수업을 정리한 내용입니다.

1. Linear Transformation

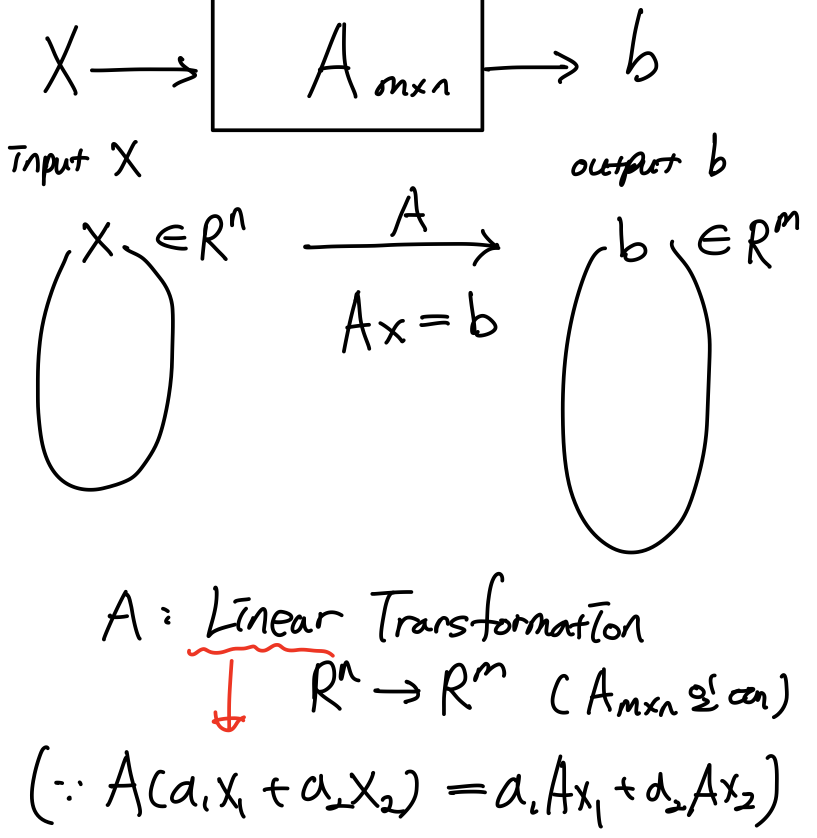
오늘은 Ax=b를 다른 관점으로 본다. 행렬 A를 system으로 보고, X를 input vector, b를 output vector로 생각한다.

그러면 A가 m*n 크기일 때, Ax=b는 n차원 공간 vector(X)를 m차원 공간 vector(b)로 변형하는 관계로 생각해볼 수 있다. 따라서 A를 Linear Transformation vector라 한다.

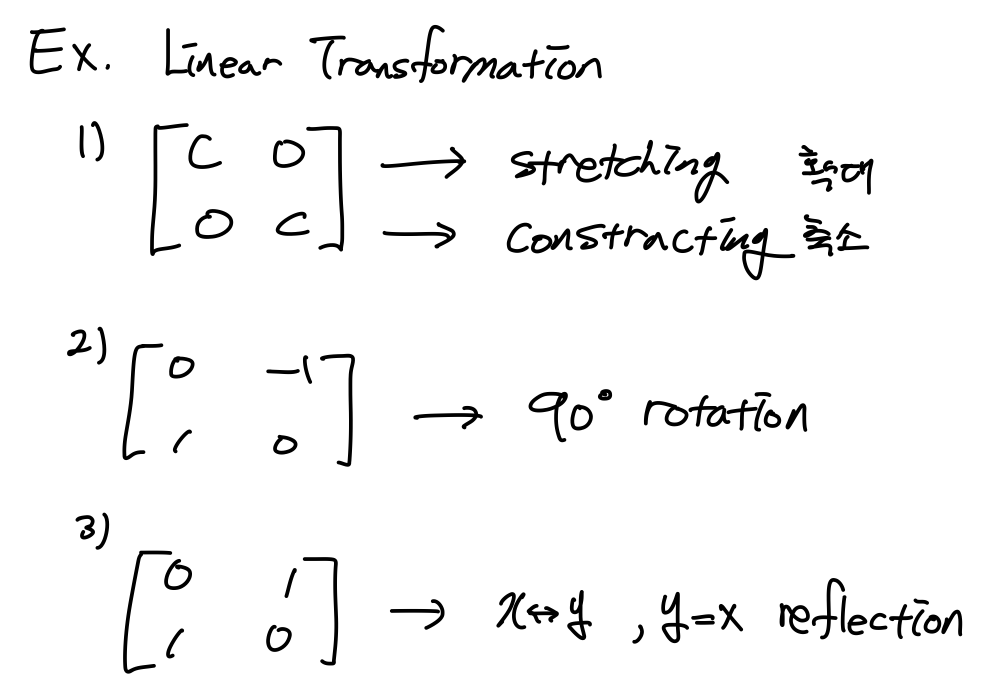
Linear Transformation 예를 보자.

Linearity(선형성)이 보장되는 모든 연산(미적분), 수식 등은 모두 linear Transformation, 행렬식으로 바꿀 수 있다.

위와 같이 Linear한 operation을 정의할 수 있으면 모두 Linear Transformation이라 할 수 있다. 그렇다면 Linear Transformation이라 하는 행렬A를 구해보자.

If given Ax for every basis vectors X
$Ax_1 = a_1, Ax_2 = a_2, ... Ax_n = a_n$
then, we can find any transform results in the vector space without A

$y = C_1X_1+C_2X_2+...+C_nX_n$
$Ay = C_1AX_1+C_2AX_2+...+C_nAX_n$
      $=C_1a_1+C_2a_2+...+C_na_n$

이것이 무엇을 의미하는지는 system 관점에서 보면,

1.1 How to find A?

If we know the Ax for the elementary basis vectorts

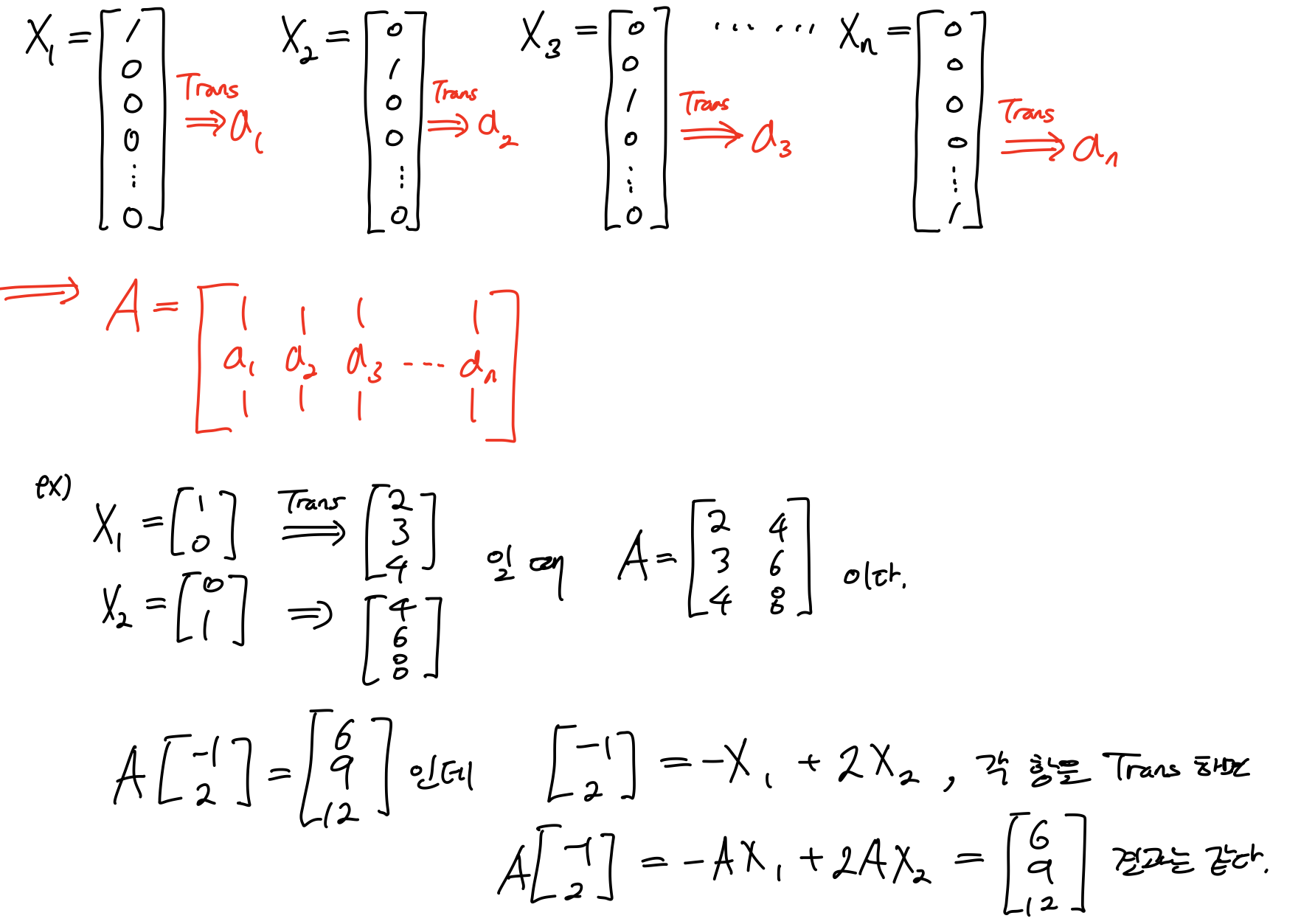
이때 주의할 점은 basis vector가 elementary basis vector가 아니면 Transform된 결과를 행렬A의 column vector에 사용하면 안된다.

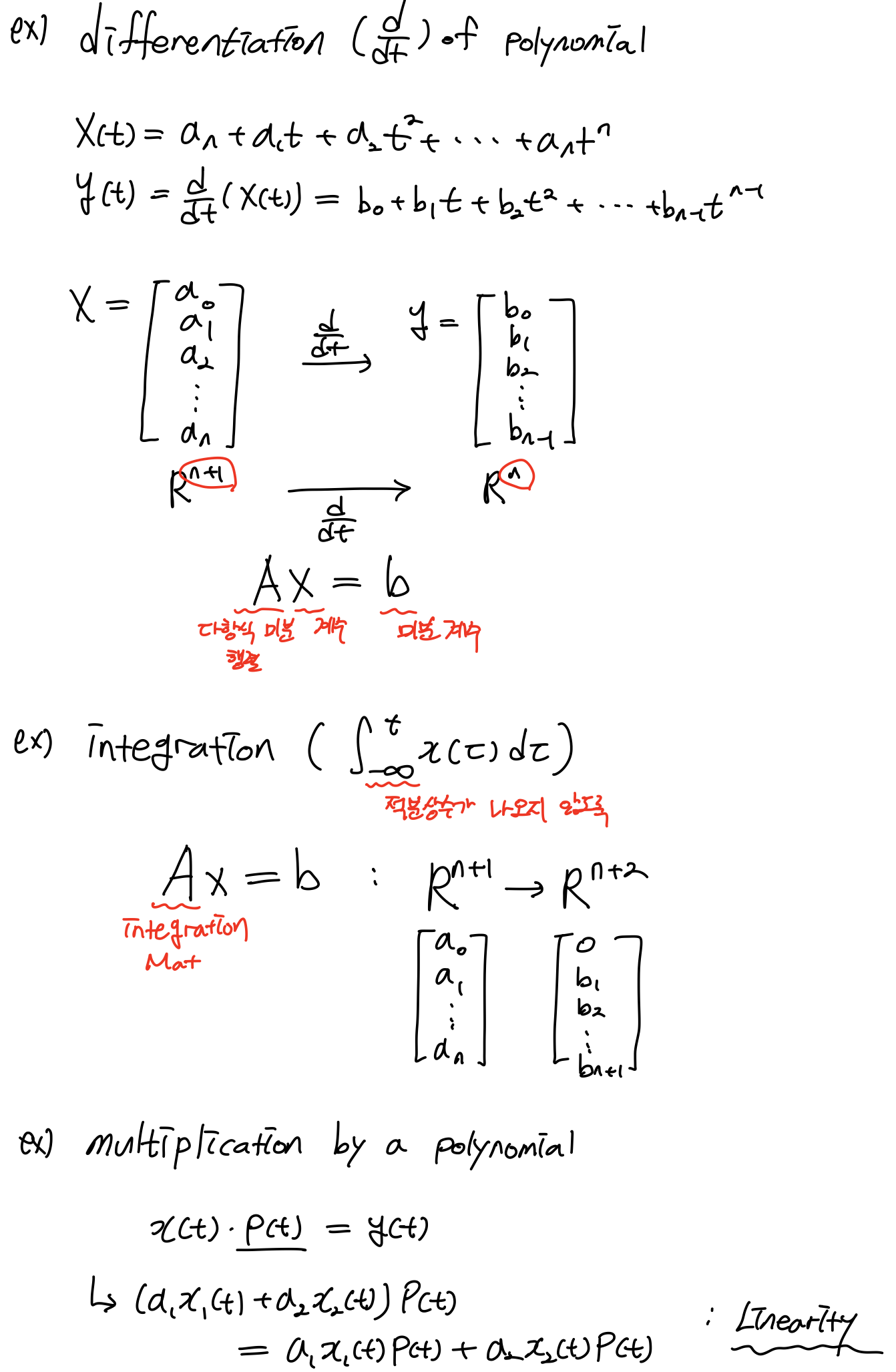
앞으로는 미분, 적분도 linear transformation이니 다항함수에 대해 적용하여 미적분을 행렬A로 표현할 수 있는 것을 해본다.

1.2 Polynomial Differentiation & Integration

행렬A가 differentiation인지 operation 자체에 의미를 모른다 해도, system A가 위와 같이 주어지고 임의의 $a_0, a_1, a_2, a_3$ 계수가 주어져있으면 4개의 계수가 들어간 다항식을 미분한 것처럼 특정한 시간 t에 대해서 기울기를 구하는구나!! 하고 알 수 있다는 것이다.

이번에는 정적분에 대해 해본다.

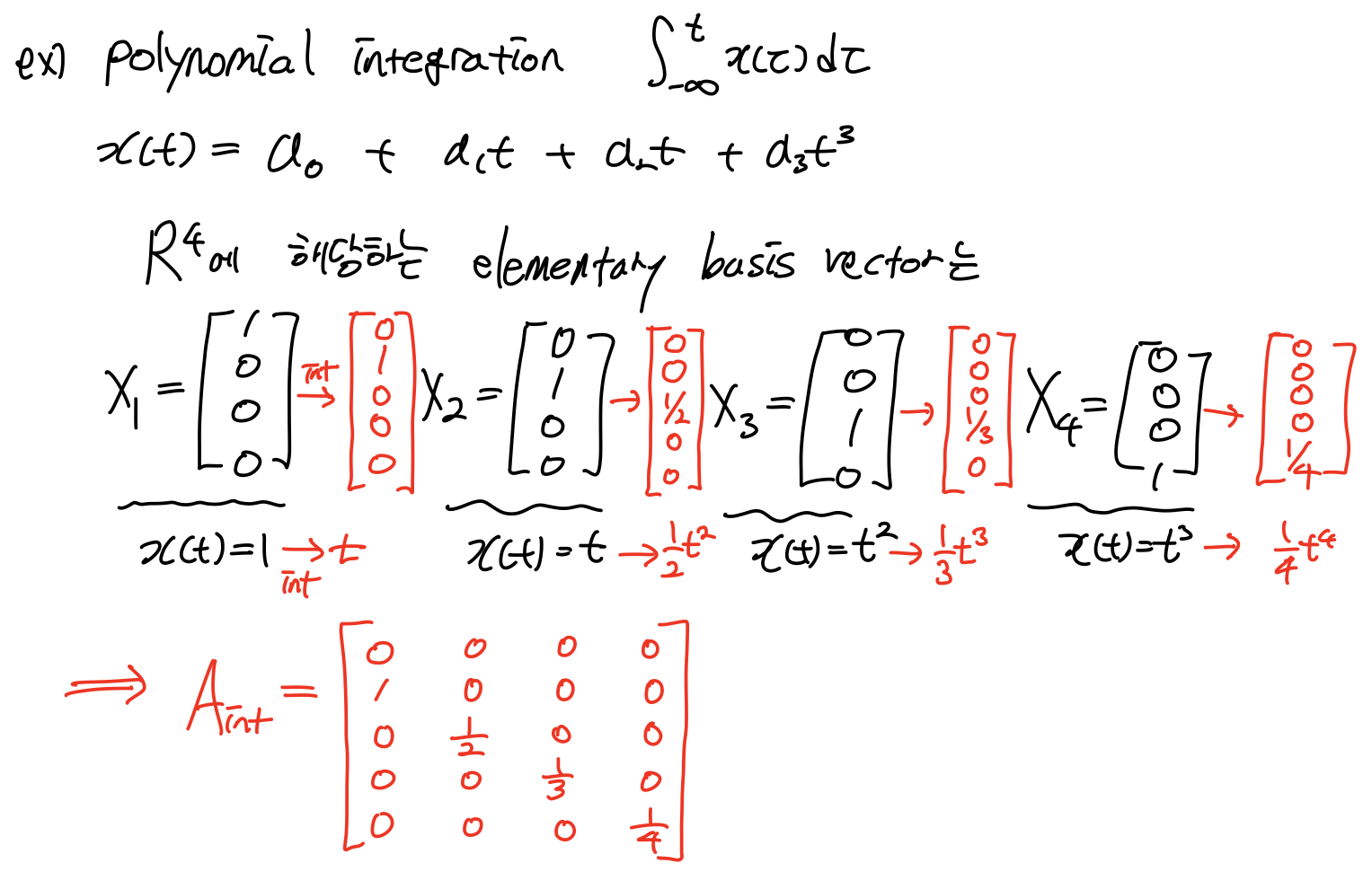
Integration은 Null space가 vector space에서 원점 하나이다. 그리고 $A_{diff}*A_{int}$은 자기자신이 나온다. 따라서

$A_{diff}*A_{int}*X=I이며\\ A_{diff} =left-inverse이다.$

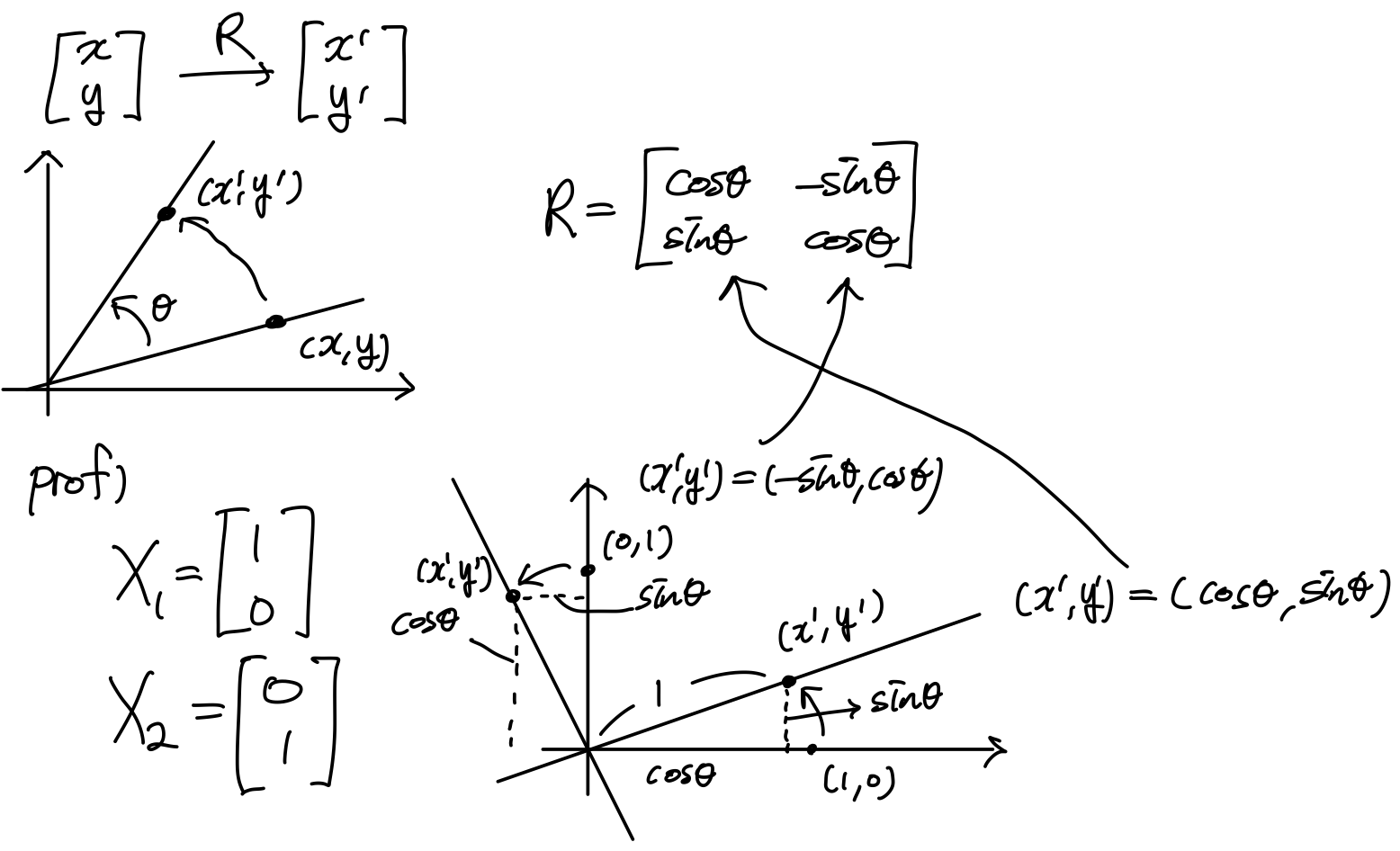
1.3 Rotation

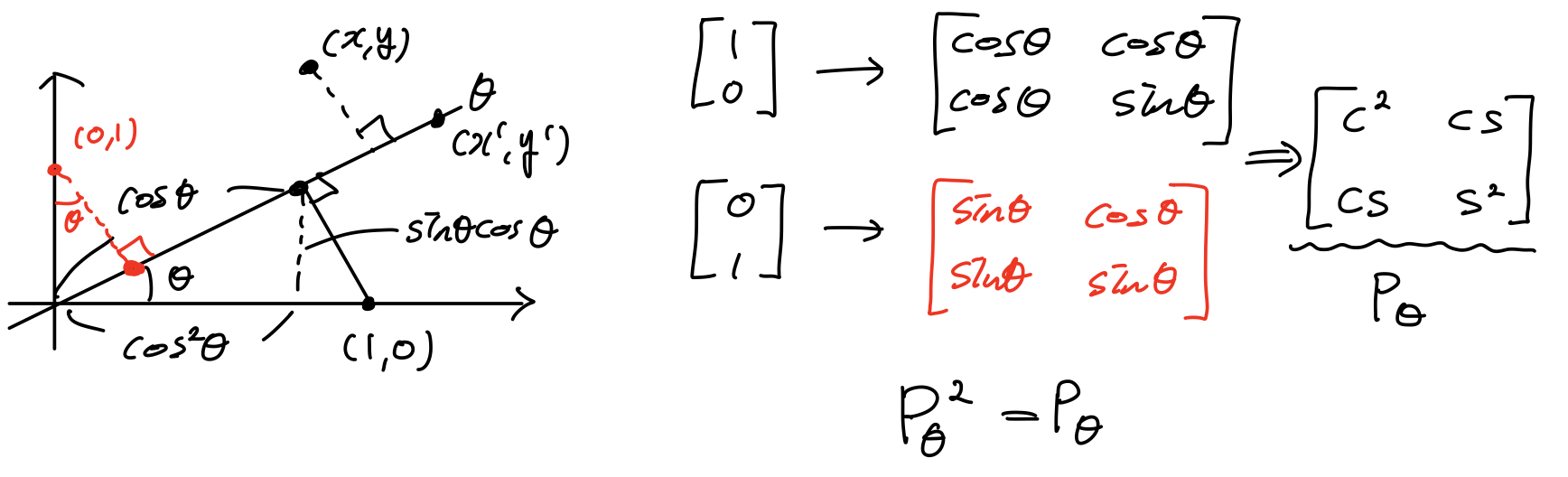
1.4 Projection onto $\theta$-line

임의의 점 (x,y)를 x축과 $\theta$를 이루는 직선 $\theta-line$에 수선의 발이 되도록 투영된 (x',y')을 Projection한다고 한다.