"모두를 위한 열린 강좌 KOCW"에서 제공하는 한양대학교 이상화 교수님의 선형대수 수업을 정리한 내용입니다.

Review

3 basic properties determinant

1. det( I ) = 1
2. Row exchange $\rightarrow$ change sign
3. 1st row linearly dependent

위 3가지 기본 판별식 특성을 이용해 다양한 특성을 더 만들어 낼 수 있다. 그 중 하나를 보자.

2nd row linearly dependent?

오호~보아하니 1st row만 linearly dependent한 것은 아닌걸로!!

row zero vector $\rightarrow$ det(A)=0인데, column zero vector $\rightarrow$ det(A)=0일까?

Determinant formule

1단원에서 Gauss Elimination한 행렬의 product of all pivots이 determinant가 된다는 것을 알았다. 이것은 행렬A를 decomposition LDU한 것을 det 취하면 증명할 수 있다. 단!! G.E 과정에서 pivoting이 없었다는 가정 하에 (1)을 증명할 수 있다.

그렇다면 pivoting을 했다면?? pivoting 행렬 permutation matrix P를 곱한 PA=LDU를 이용해 해결할 수 있다. 결국 pivoting 횟수에 따라 부호가 바뀌는 것이다. pivot의 곱으로 나타낼 수 있다.

예를 들어보자. 아래와 같이 생긴 행렬을 Spare Matrix라고 부른다.

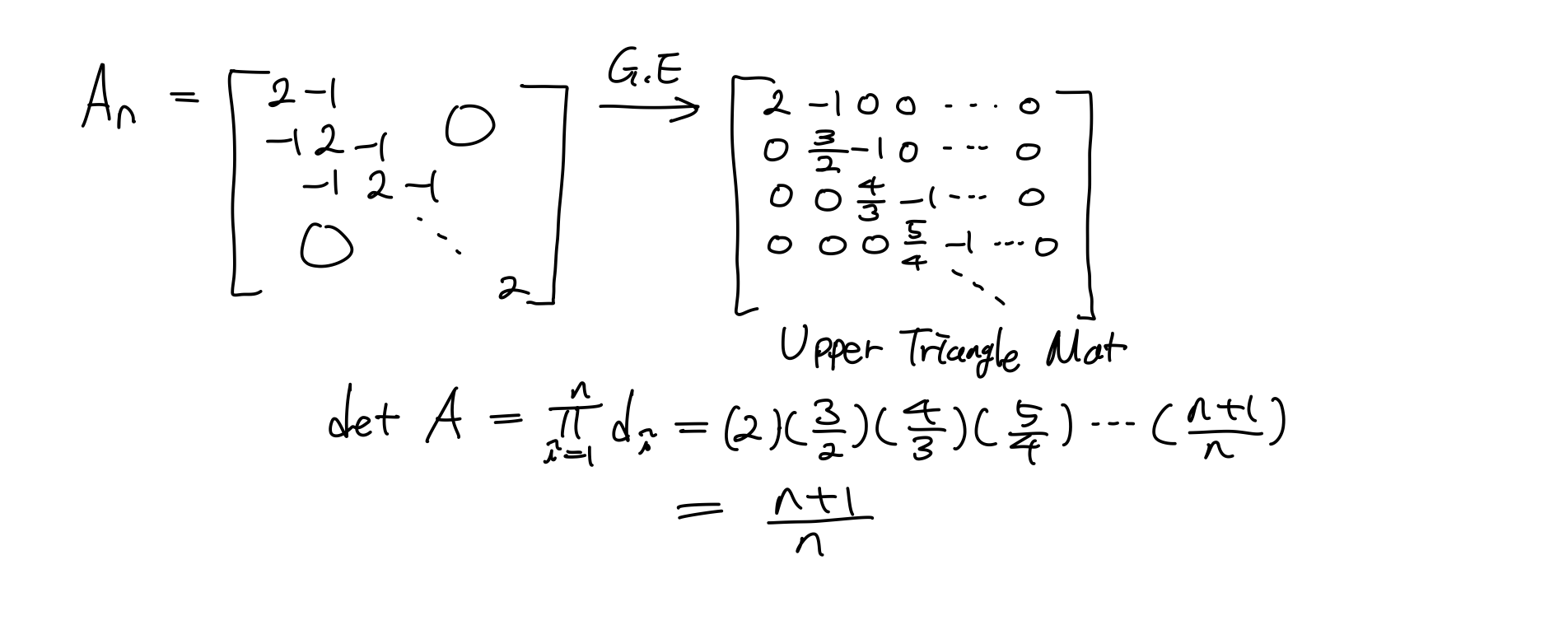
Big Formula

자, 이제 새로운 공식을 유도해보자!

1. det A depends linearly on the first row
2. zero column $\rightarrow$ det A = 0
3. det A depends linearly on the any rows

쉽게 말하면 determinant는 모든 행에 대해 linearly dependant하며, zero-row 혹은 zero-column이 있다면 detetminant는 0이 된다.

먼저 2x2행렬에 대해 공식이 맞는지 알아보자.

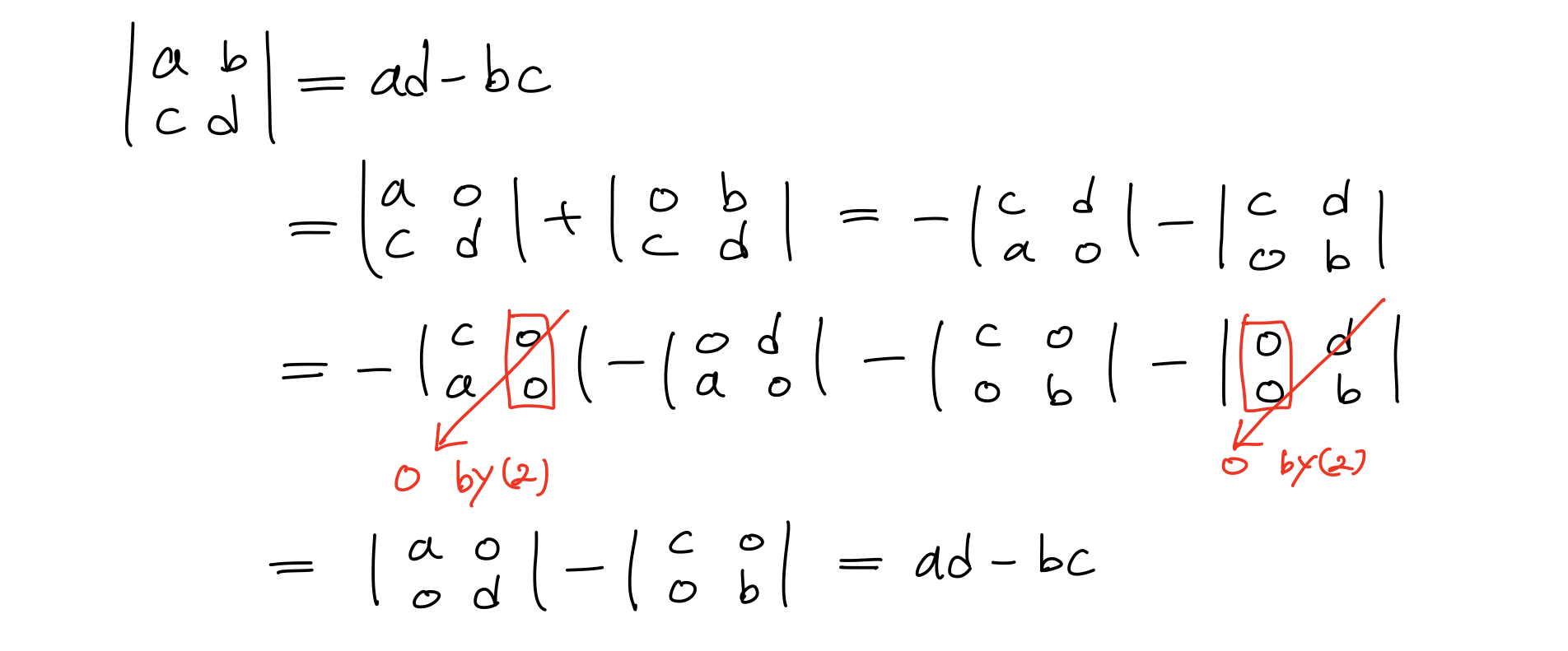
2x2를 만족하는 것을 보았으니, 이제 3x3에 대해 보자.

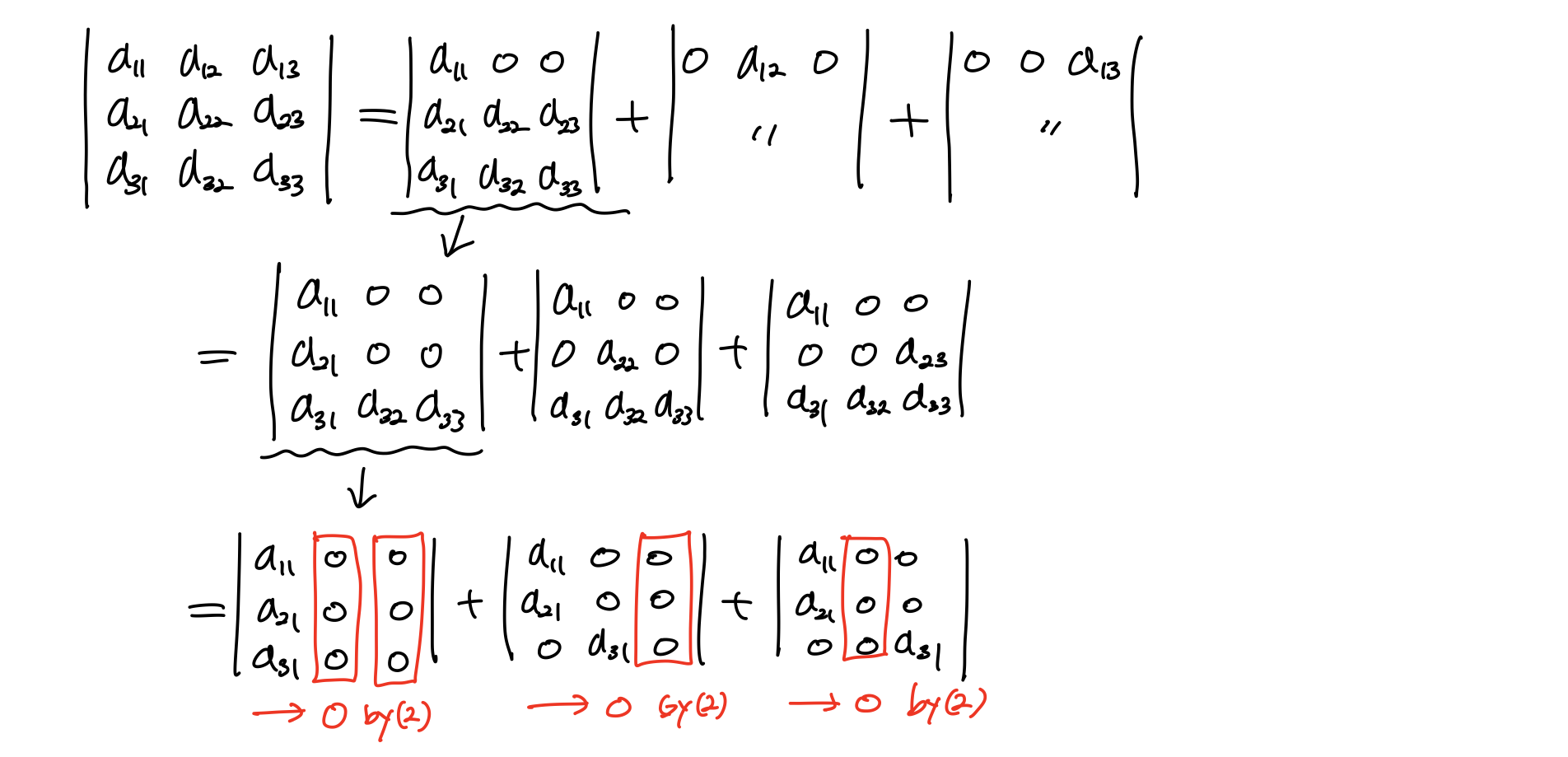
결국 모든 행과 열에 하나의 elements만 있는 determinant만 살아남을 수 있다.

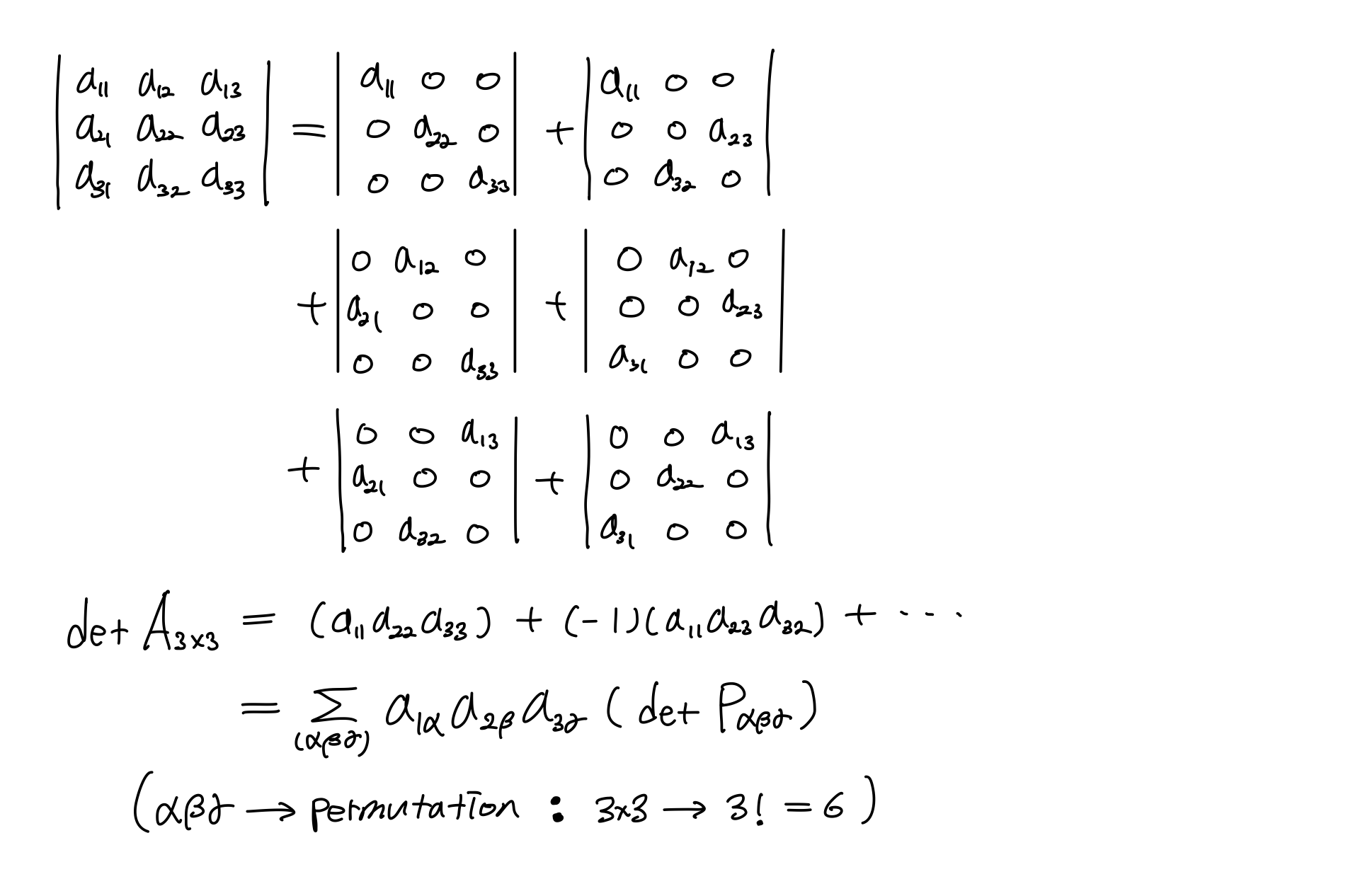
이를 정리하면

우리는 이것을 Big Formula라고 부른다. 이를 통해서 $n \times n$ 행렬에 모두 적용이 가능하다. 이것을 조금 더 쉽게 표현해보자.

Consider all the terms involving $a_{11}$

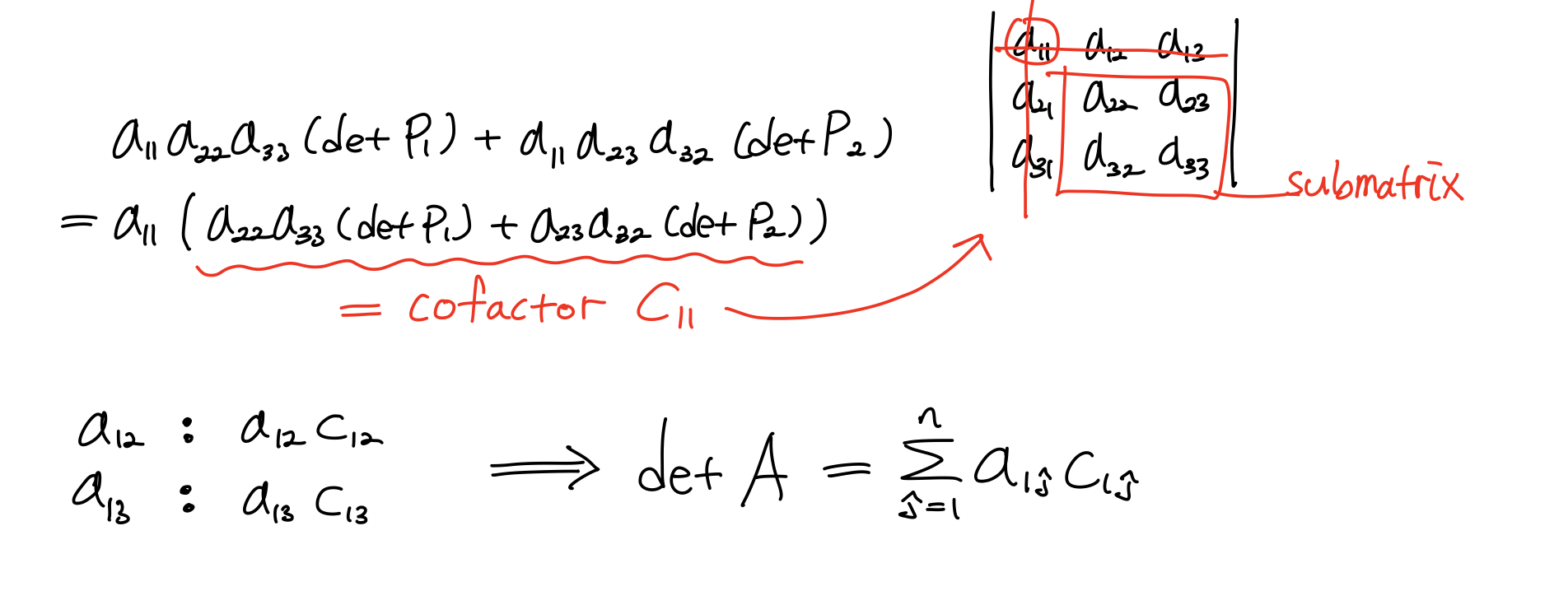
이때 Cofactor 개념이 나온다. 선택된 element의 행과 열을 제외한 행렬을 Submatrix = Minor Matrix라고 할 때 Cofactor는 다음과 같다.

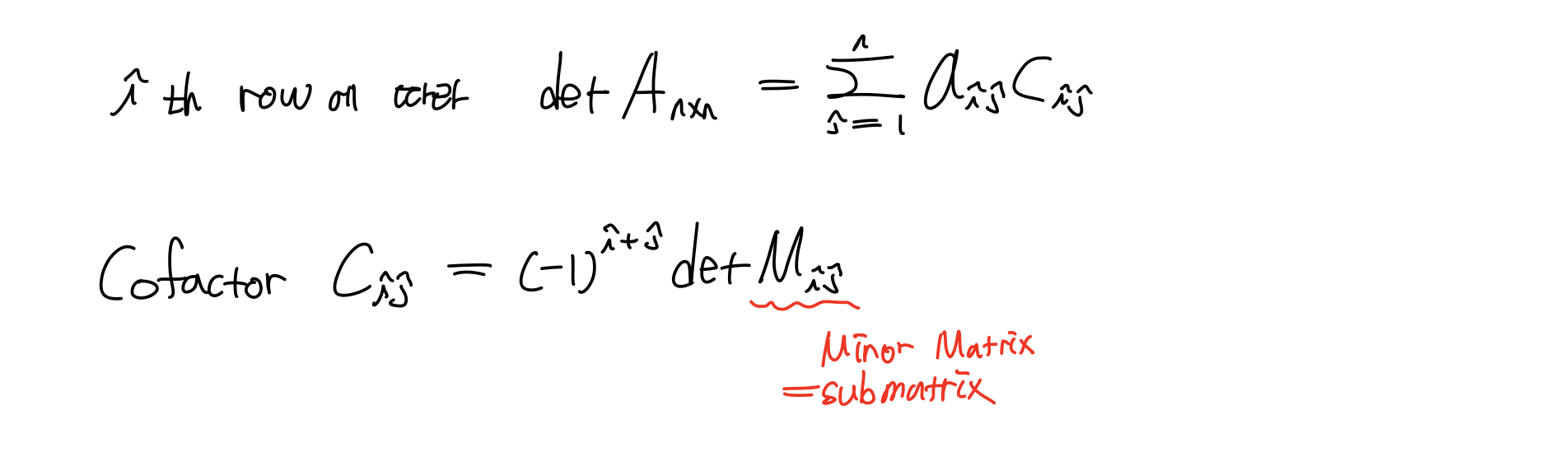
따라서 0이 많이 속해 있는 row를 선택하는 것이 연산에 유리하다. 개꿀~

Example