"모두를 위한 열린 강좌 KOCW"에서 제공하는 한양대학교 이상화 교수님의 선형대수 수업을 정리한 내용입니다.

Review

이전까지 determinant를 구하는 방식 3가지에 대해 알아보았다. 기억이 안날테지...그래서 준비한 Review!!

• Gauss Elimination

  $det\ A=product\ of\ pivots=(-1)^{number\ of\ row\ exchanging}\prod_{i=1}^N d_i$

• Big Formula

  $det\ A=\sum_{\alpha\beta\gamma...\nu}^{n!}a_{1\alpha}a_{1\beta}a_{3\gamma}...a_{n\nu}$

• Cofactor

  $det\ A=\sum_{j=1}^{n}a_{ij}C_{ij}=\sum_{j=1}^{n}a_{ij}(-1)^{i+j}det\ M_{ij}$

위의 3가지가 determinant를 구하는 방식이었다. 그러면 determinant를 응용하는 것에 대해 알아보자.

Determinant Applications

Inverse Matrix

첫 번째는 역행렬을 Cofactor Matrix를 이용해 구하는 것이다. 이때 $C$는 Cofactor Matrix로, cofactor로 이루어진 행렬이다.

Cofactor Mat를 이용하면 다음의 공식(?)이 성립된다.

이것을 증명해보자. 먼저 위 공식을 $det\ A$에 대해 풀면

가 된다. 우항을 풀어보면

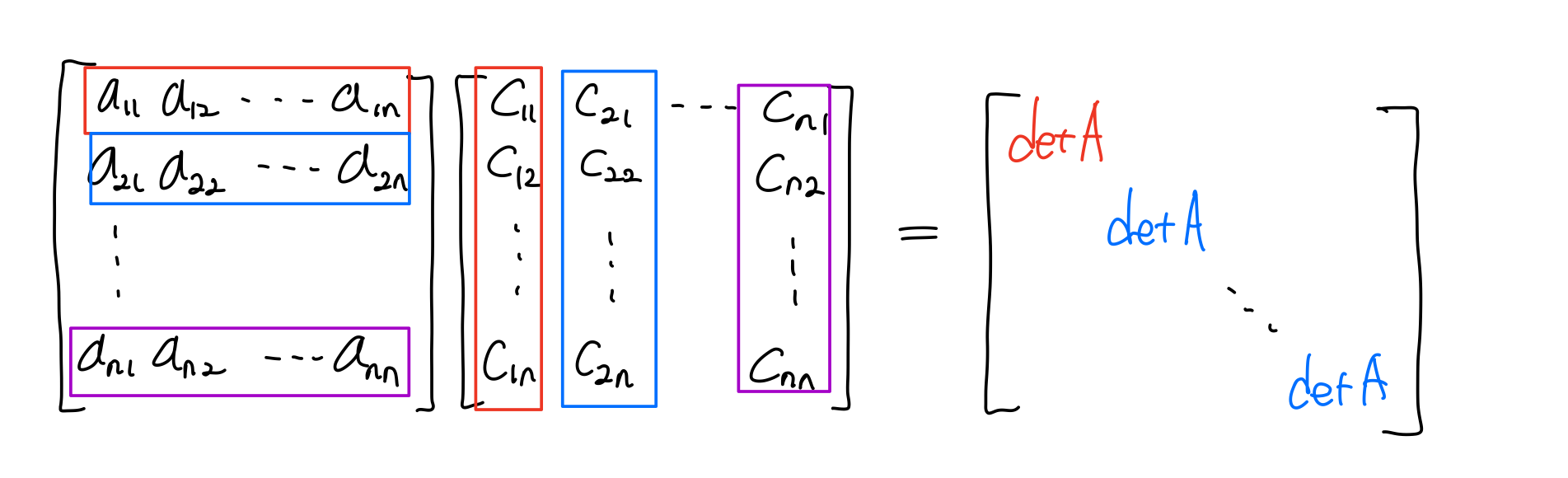
digonal elements는 Cofactor를 이용해 determinant를 구하는 것과 동일하다는 것을 알 수 있다. 그렇다면 나머지 elements는 어떨까?

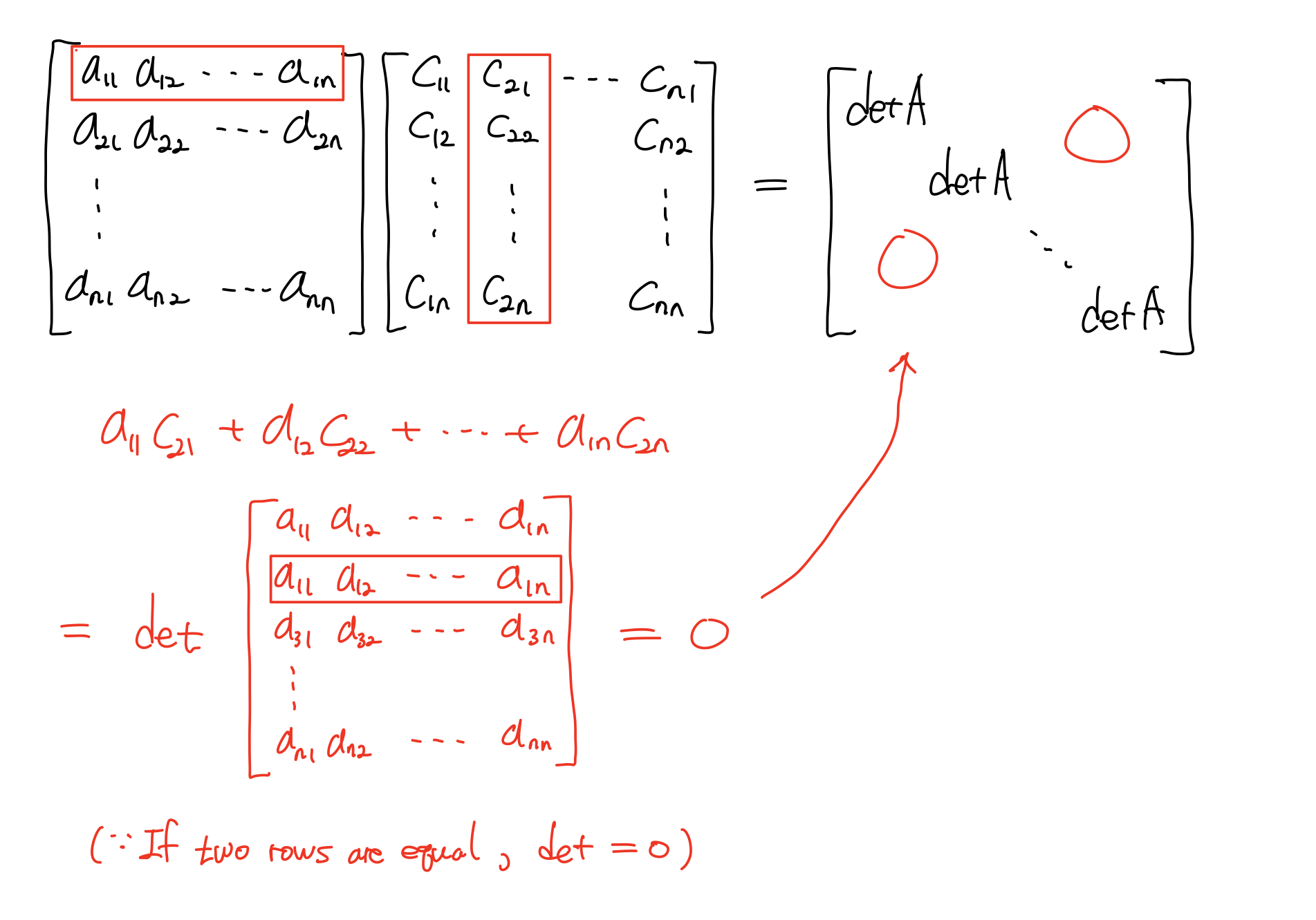
이 역시 Cofactor로 determinant를 구하는 것과 유사하다. 다만, 1행2열의 풀이를 보면 2행과 1행이 같은 행렬의 determinant를 구하는 것과 같다. 그렇다면!! 지난 강의에서 알아본 determinants properites 중

에 의해 0이 된다.

Cramer's Rule

결론부터 말하자면 Cramer's Rule은

이다. 이게 뭐지 싶다면 쭈우우욱 되돌아가 보자. 선형대수의 목적은 Ax=b의 해를 구하는 것이다.

자 이것을 기억하고,먼저 $B_i$에 대해 알아보자.

행렬A에서 i번째 column vector에 b elements가 들어가는 것이다. 그리고 기억했던 식을 정리하면

이 식의 분자 $C^Tb$를 풀이하면

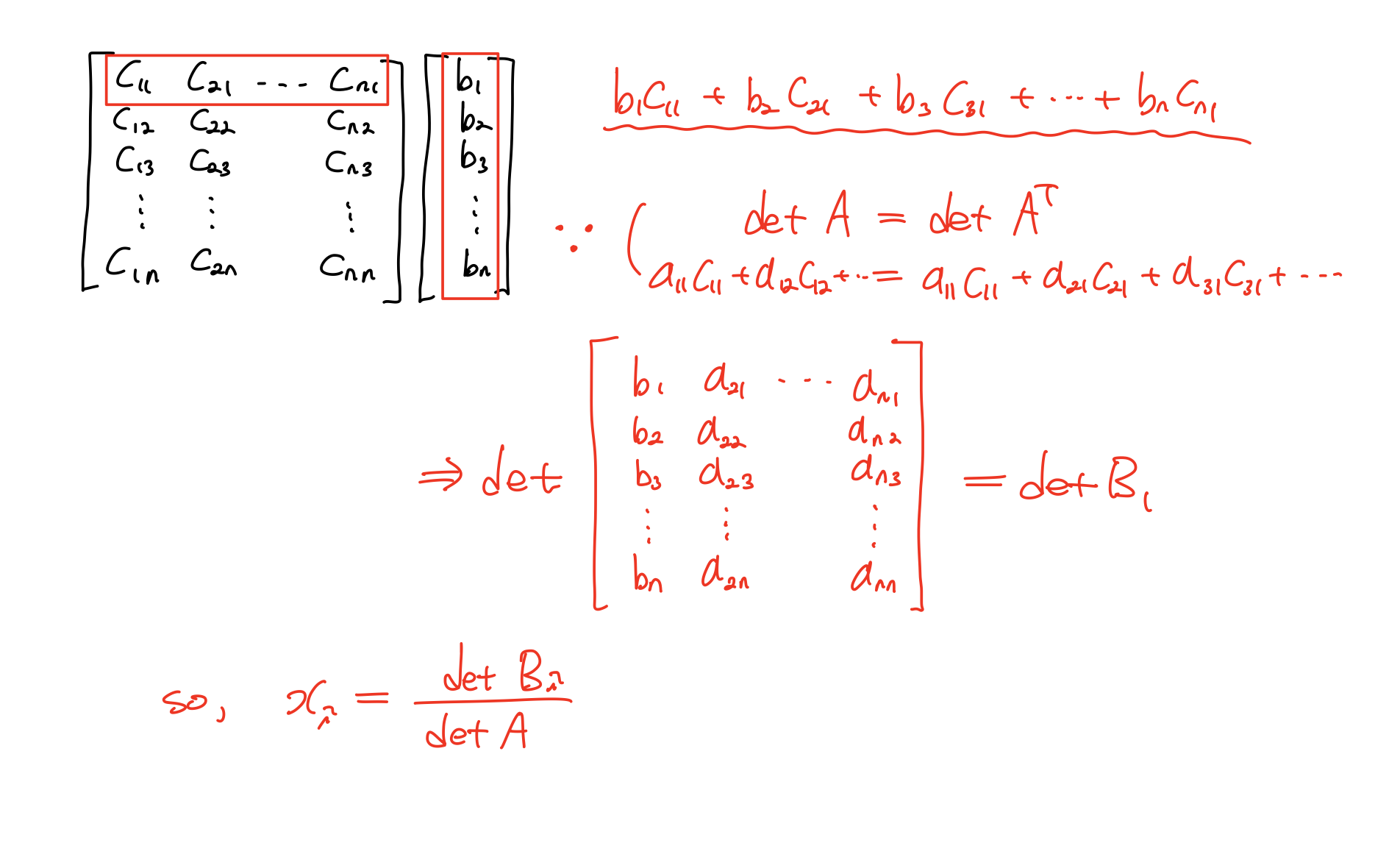
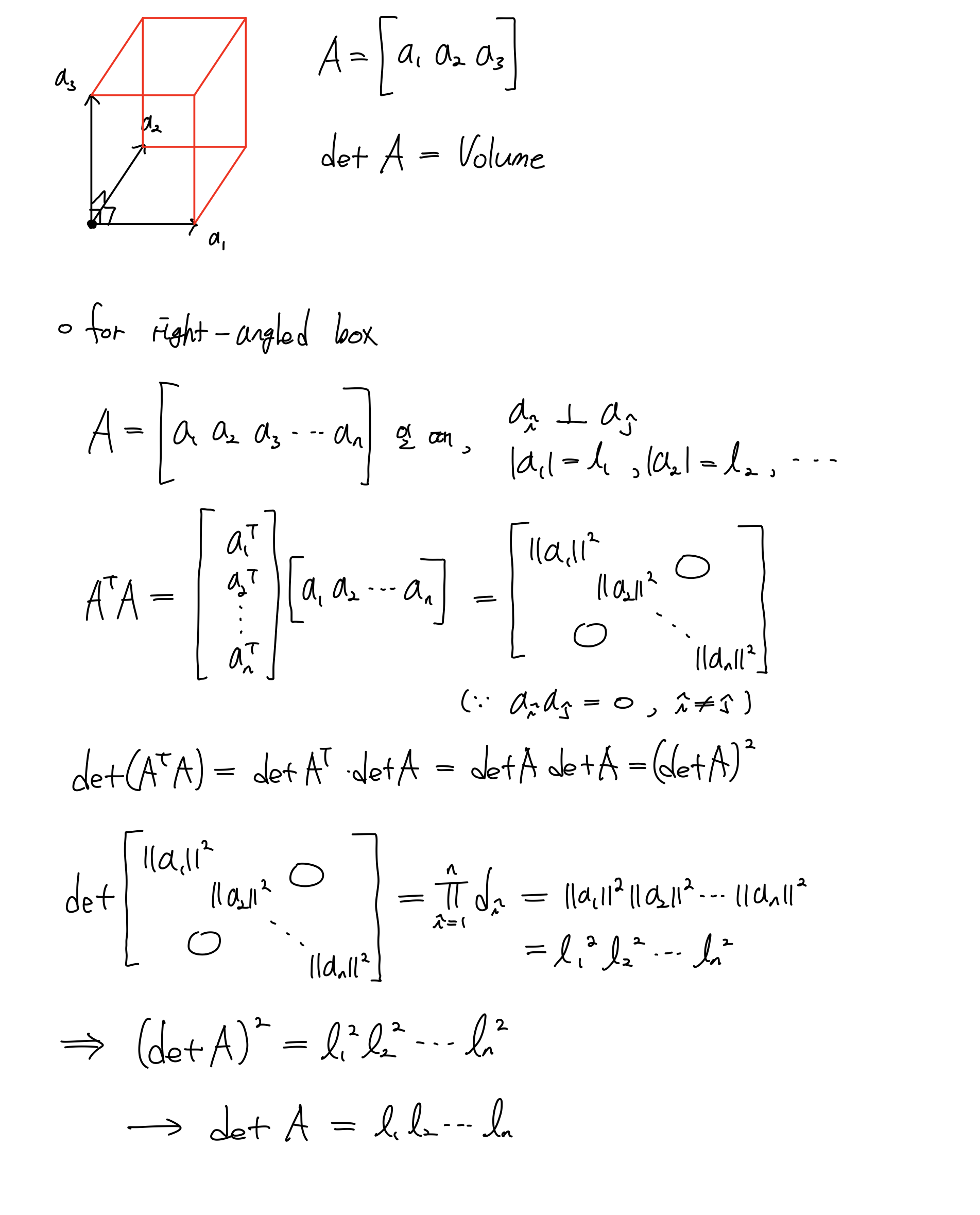
Volume of Box