"모두를 위한 열린 강좌 KOCW"에서 제공하는 한양대학교 이상화 교수님의 확률과통계 수업을 정리한 내용입니다.
Review
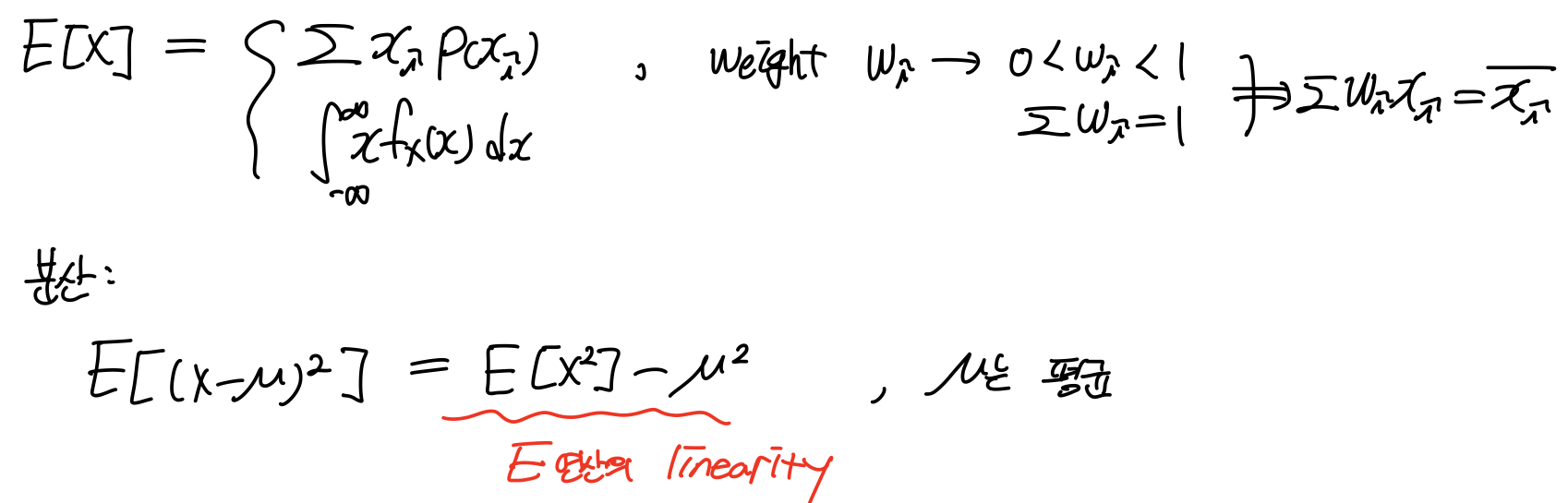
1. Geometric ditribution
RV K : #of trials until the 1st success

1.1 Geometric distribution 분산

평균값은 로, 평균은 수 많은 경우 중 average이니 이 직관적이다. 하지만 분산은 으로 직관적이지는 않다. 얼마나 평균에서 퍼져있는 정도를 나타내는 값이니까.
우리가 관찰하는 어떤 시스템의 랜덤한 현상이 어떤 방식으로 동작하는지 찾다보면, 배운 특수한 distribution으로 modeling이 가능하다. 그런 것들을 위와 같이 특별한 확률분포로 표현하는 것이다.
2. 평균과 분산이 갖는 의미
평균과 분산이 랜덤한 시스템에 대해 어떤 의미를 갖는지 알아보자.
예를 들어, 화면 속에 나타난 사람의 얼굴을 판단하기 위해서는 판단의 기준이 있어야 한다. 이것은 함수나 숫자와 관련이 있어야 한다. 얼굴임을 나타내는 참값이 있다고 하면, 이것은 표준(혹은 예측, 추정)과 실제 값의 차이를 구하는 것이다. 그 값이 음수일 수 있으니 제곱을 해준다.
하나의 값이 아니라 여러 데이터에 대한 값을 구하는 것이니 모든 데이터의 오차 제곱승을 더해준다. 그것이 minimize하도록 찾아주는 것이다. 이를 보통 error model이라 하고 그 제곱을 energy라고 한다.
f라는 함수가 있다.
이때 f를 mimimum되도록 하는 x값은 이다. 그렇다면 f가 다음과 같을 때는 어떨까
이때 f를 mininze해주는 x는
이다. 이는 평균 이다. 평균을 함수에 대입하면,
분산이 된다.
그러면 를 특정한 확률값을 갖는 RV이라 생각하면,
확률P를 곱해주면 된다. (단, 이때는 descrete RV라 생각)
평균 또한,
이 된다.
3. Conditional Mean

조건부에서 조건은 새롭게 제안적으로 정의된 Sample space(전체집합)이다. 따라서 Sample space A에 벗어나지 않는 조건에 의해서 평균을 구한다.
Descrete case는 앞에서 배웠던 조건부확률과 조건 이 다르다. Continuous case는 contional PDF를 conditional CDF로 표현한다. CDF 자체가 확률이기 때문이다. 그러면 그것을 확률모델로 바꿀 수 있다.
3.1 예제
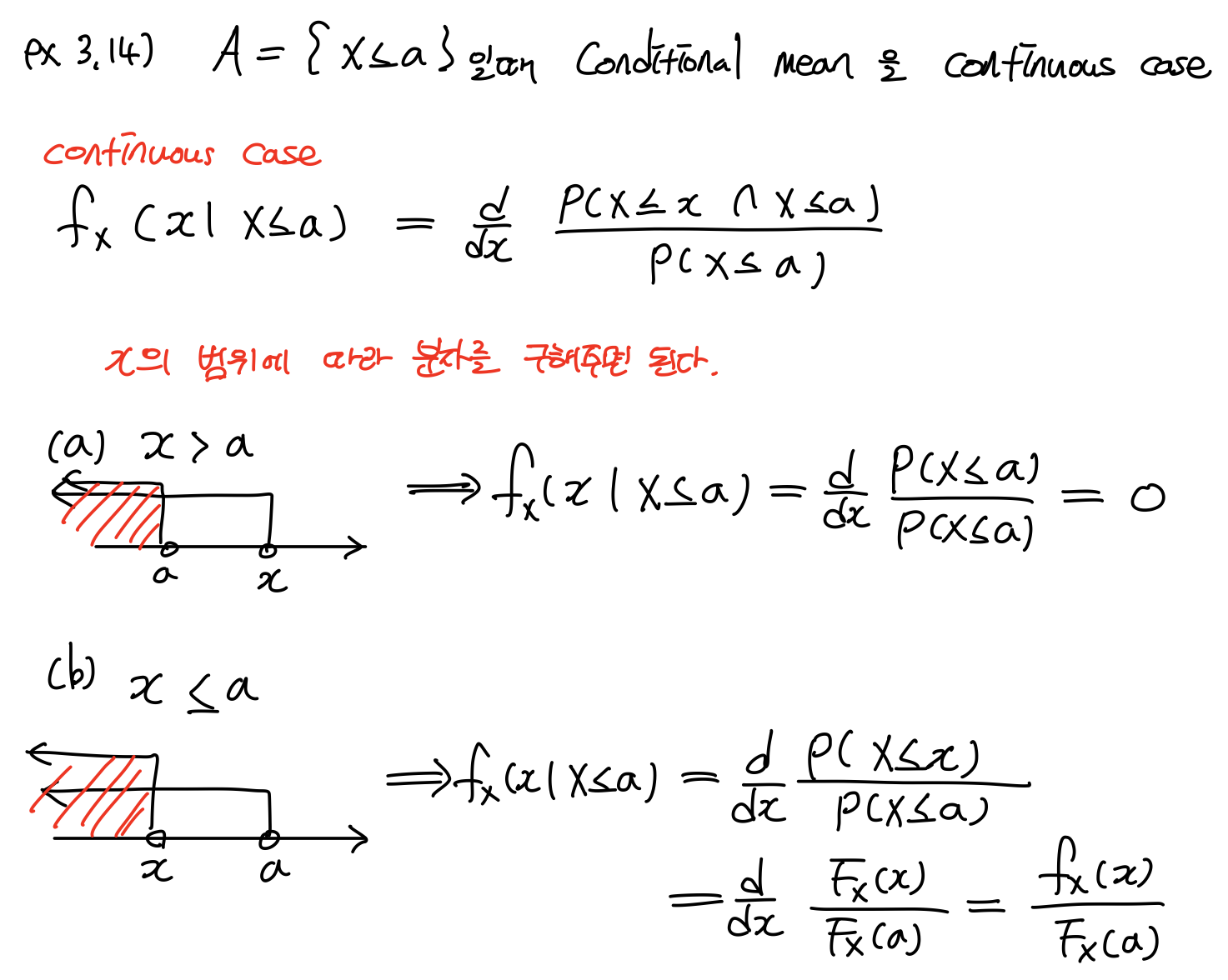
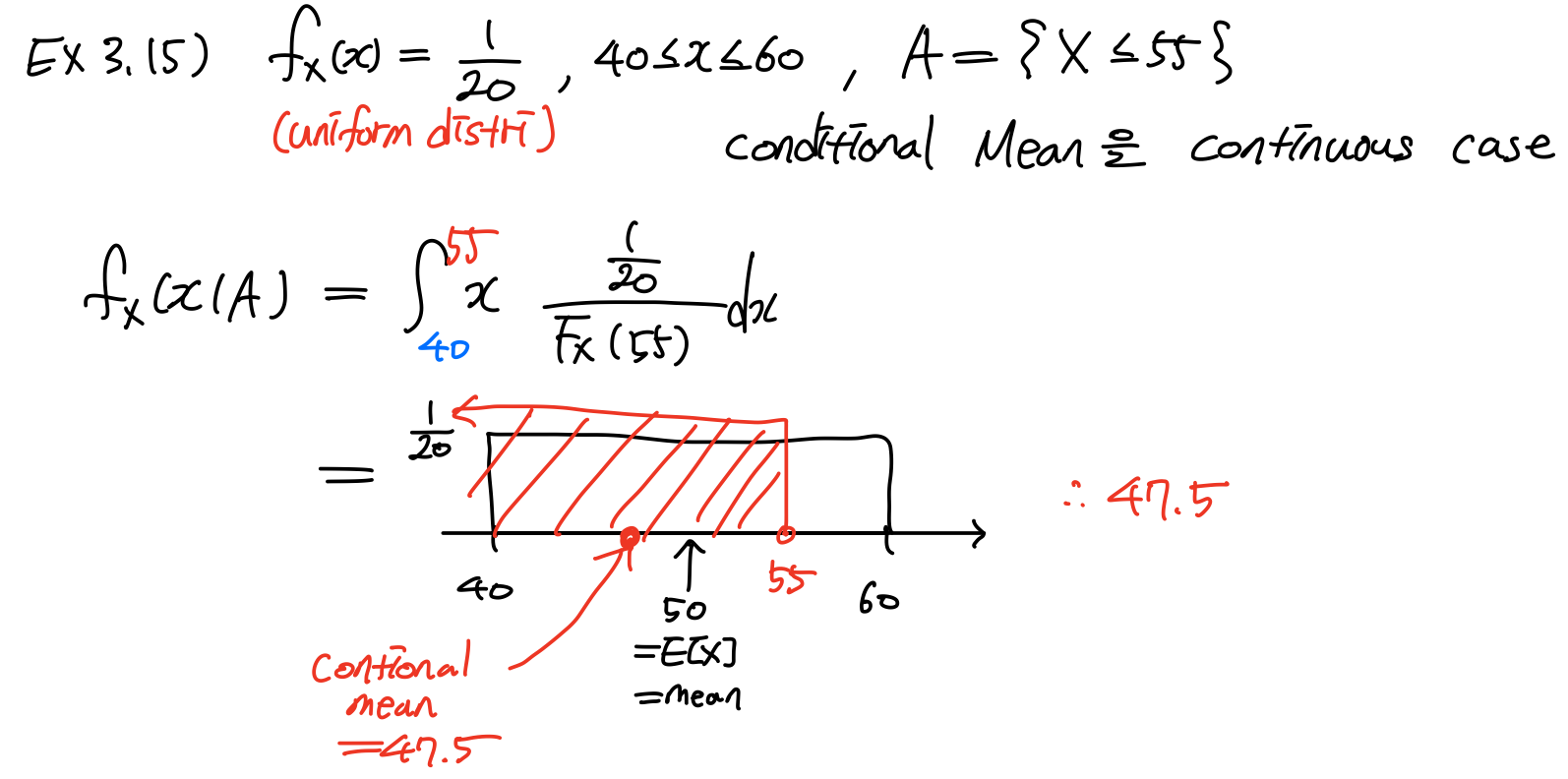
Uniform distribution case는 모든 X에 대해 같은 크기의 확률을 가지고 있으므로 conditional 범위만 생각해주면 어렵지 않게 구할 수 있다.