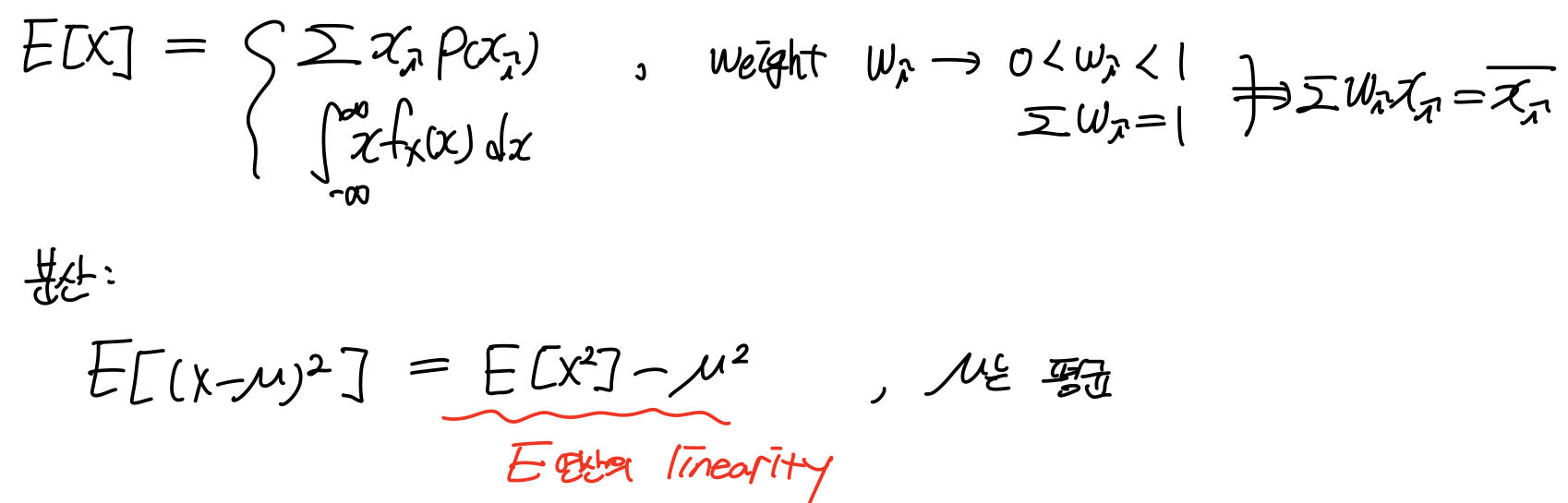
"모두를 위한 열린 강좌 KOCW"에서 제공하는 한양대학교 이상화 교수님의 확률과통계 수업을 정리한 내용입니다.
Expectation = mean. 어떤 랜덤하게 나오는 확률, 변수값의 평균이 왜 중요한가?
랜덤하게 나오기 때문에 예측할 수 없다. 랜덤한 현상으로부터 어떤 값을 결정하려면 방법이 필요하다. 어떤 값이 나올지 모르니, 랜덤한 값을 하나 생각해보자.
그리고 실제 값
예를 들어, 주사위를 던져 나올 값을 예측해 하나를 정한 것이 이고, 실제로 던져 나온 값이 . 두 값의 차이의 제곱이 작을수록 유리한 것이다. 하지만 랜덤하니 여러번 던져 평균을 구해준다. 그것이 평균값 expectation이다.
이 값이 minimize될 때 는 뭘까? 그것이 이다. 이것이 평균이 갖는 의미이다. 모든 랜덤한 현상에 대해서 Error가 가장 적은 값, 그것이 평균이다.
1. Chevyshev Inequality
Mean이 가지는 의미를 확률적으로 이야기해 보자.
: RV X와 X의 평균값 E[X]의 차이가 어떤 실수값 a보다 크거나 같을 확률은
부등호를 만족한다.
임의로 나온 값 X와 평균값 E[X]의 차이는 특정한 실수값 a보다 클 확률이 Upper bound 이다. 확률값과 실제값의 차이를 확률적으로 정의한 것이 Chevyshev Inequality이다.
증명은 다음과 같다.
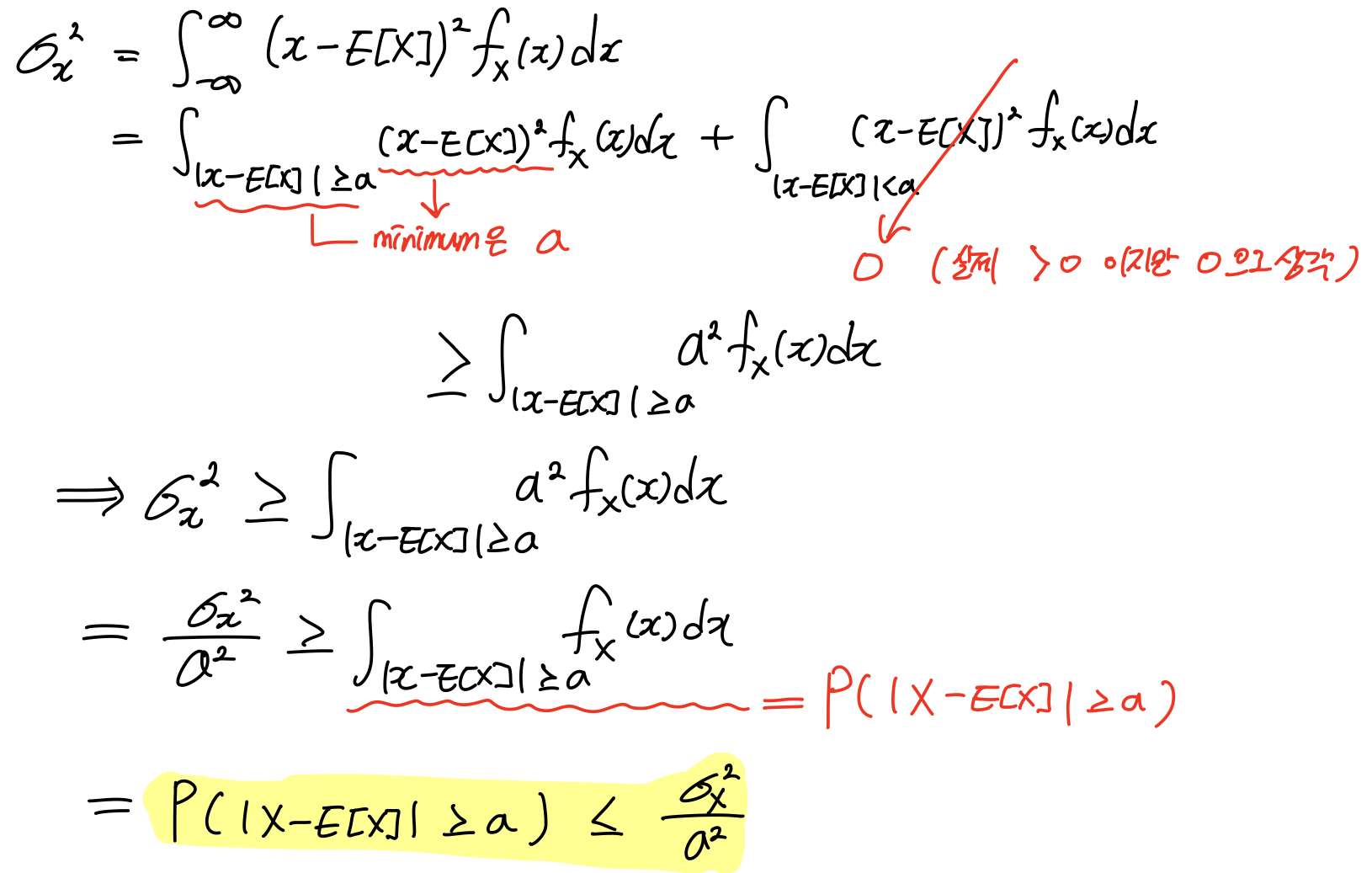
chapter 4. Special Distribution
확률함수가 정해져있는 것에 대해 다뤄보자
4.2 Bernoulli Distribution
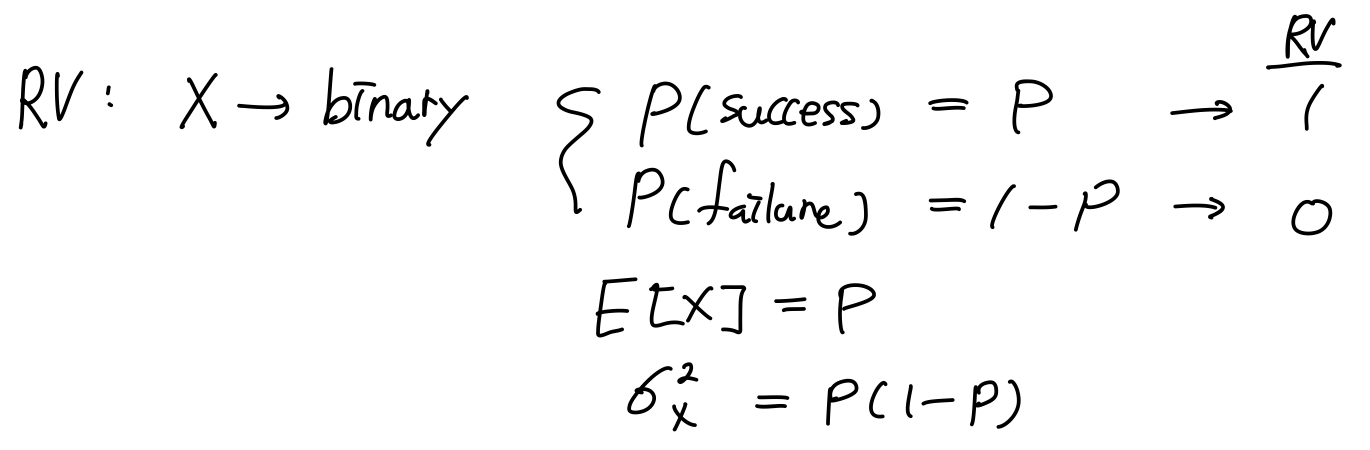
정의하고자 하는 Random Variable X가 binary하다. 단 두가지 outcome만 나온다는 뜻이다. outcome 적당한 RV에 매칭시키면 일종의 RV이 된다. 그런 분포를 Bernoulli Dist라고 한다.
4.3 Binomial Distribution 이항분포
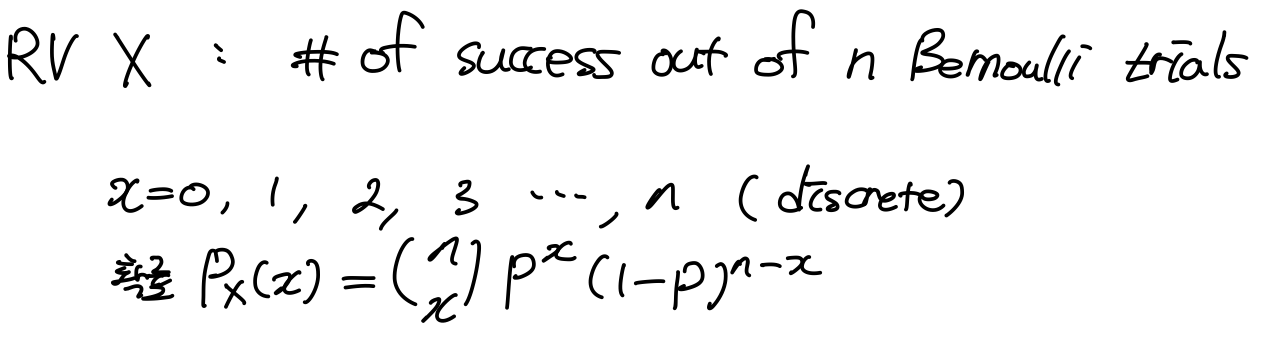
이항분포가 제대로 된것인지 이야기 하려면, RV이 어떠한 범위, 어떠한 값을 취하는지 같이 규정해 주어야 한다.
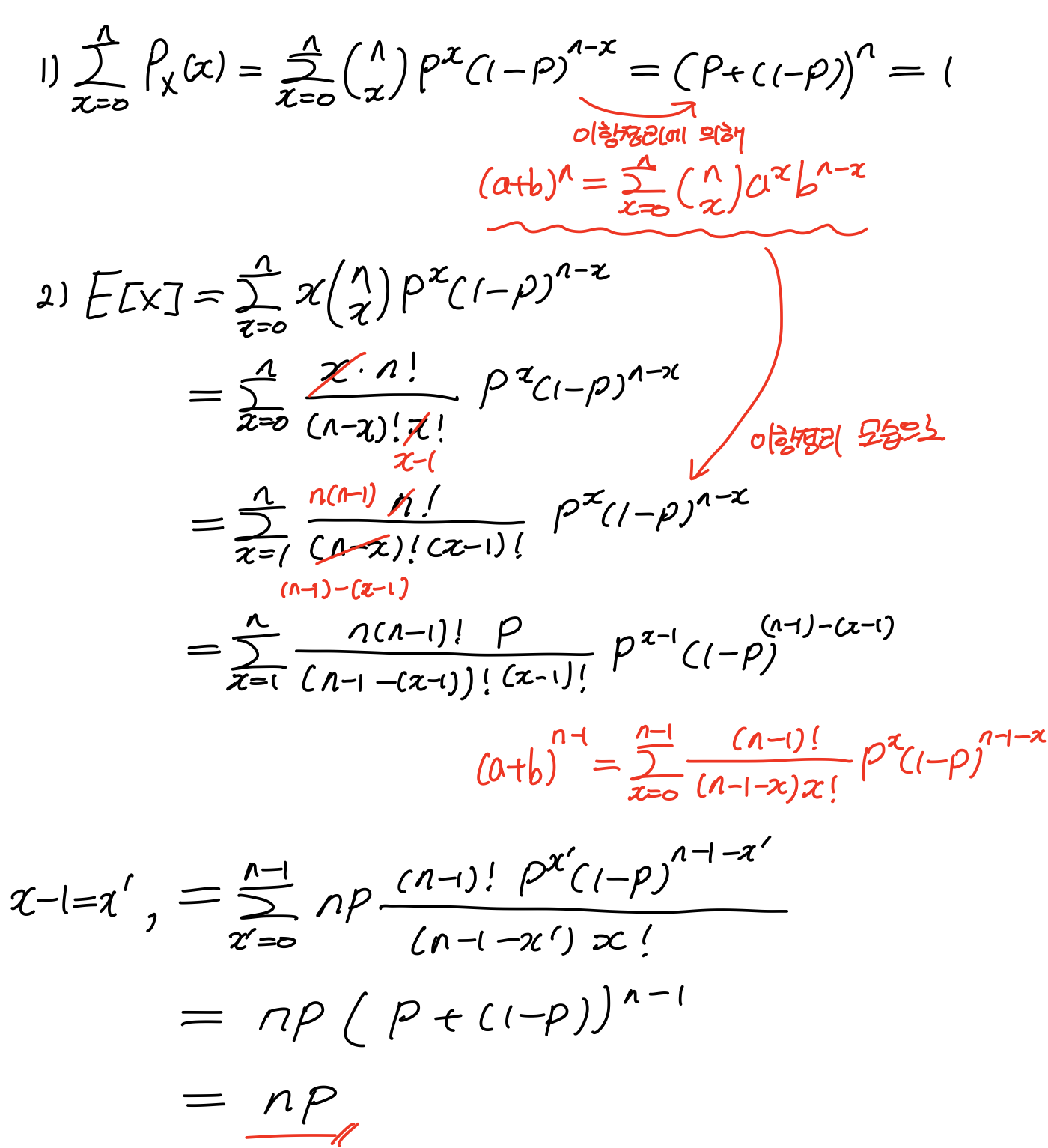

4.4 Geometric Distribution
RV X: # of Bernoulli trials until 1st success
4.4.1 Forgetfulness(Memoryless)
Geometric Dist의 대표적인 예가 주사위를 던지는 것이다. 만약 10번을 던졌는데도 원하는 숫자가 나오지 않았다 하자. 앞으로 5번을 더 던져서 원하는 숫자가 나올 확률은 얼마일까?
만약 5번을 던져서 원하는 숫자가 나오지 않았으면, 앞으로 5번을 더 던져서 원하는 숫자가 나올 확률은 또 얼마일까?
정답은 앞에서 뭔 짓을해도 앞으로의 확률에 아무런 영향을 주지 않는다. (마치 로또와 같군;;) 이것을 Forgetfulness(Memoryless)이다. 이것이 Geometric Dist에 나온다.
Consider K additional trials untis the 1st success, given n trials fail.
