"모두를 위한 열린 강좌 KOCW"에서 제공하는 한양대학교 이상화 교수님의 선형대수 수업을 정리한 내용입니다.
1. Review
1.1 Linear Independence
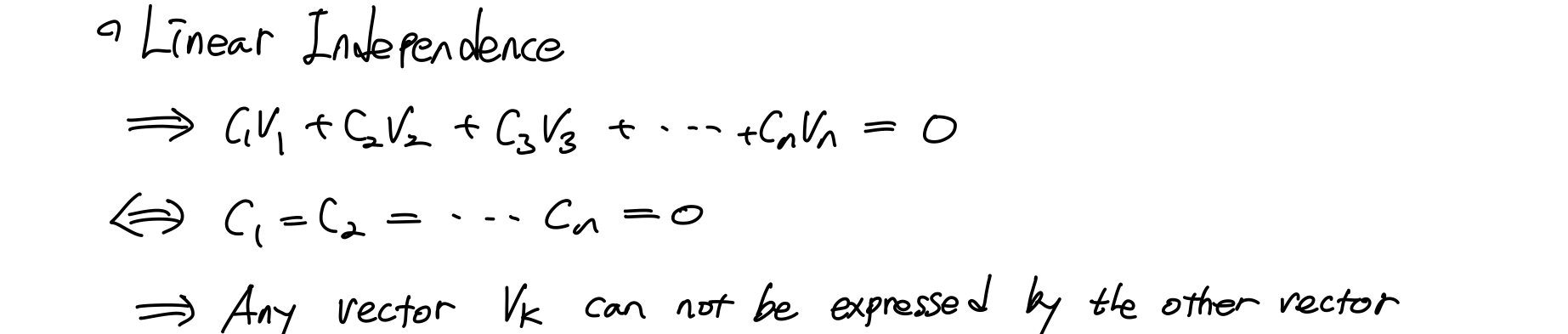
Linear Independence의 의미는 다른 vector를 가지고 특정한 하나의 vector를 linear combination해서 만들어낼 수 있느냐? "그렇지 않다" 그런 형태의 vector 모임을 Linear Independence하다라고 한다. 예를 들어,
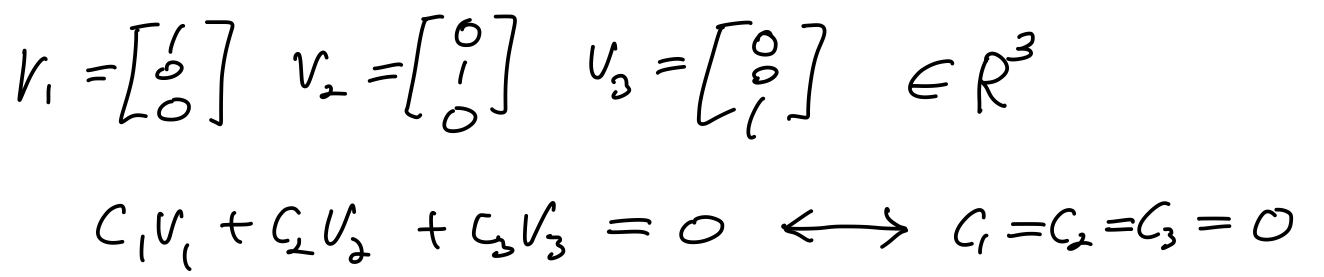
1.2 Spanning
Set of vectors constructs a vector space by linear combinations.
The set of vectors span the vector space
Span은 vector를 가지고 vector space를 만드는 모든 linear combination 과정을 말한다. 그 방법은 다양하다. 단, 어떤 vector space를 span하는 linear independente한 vector의 집합은 unique하지 않다.

그렇다면 무엇이 unique할까?
If given linearly independent vectors,
==> linear combination -> unique!
1.3 Basis
Minimum # of vectors to span a vector space.
최소한의 수로 vector space를 span하려면 vector가 모두 Independent해야 한다.
Maximum # of linearly independente vectors.
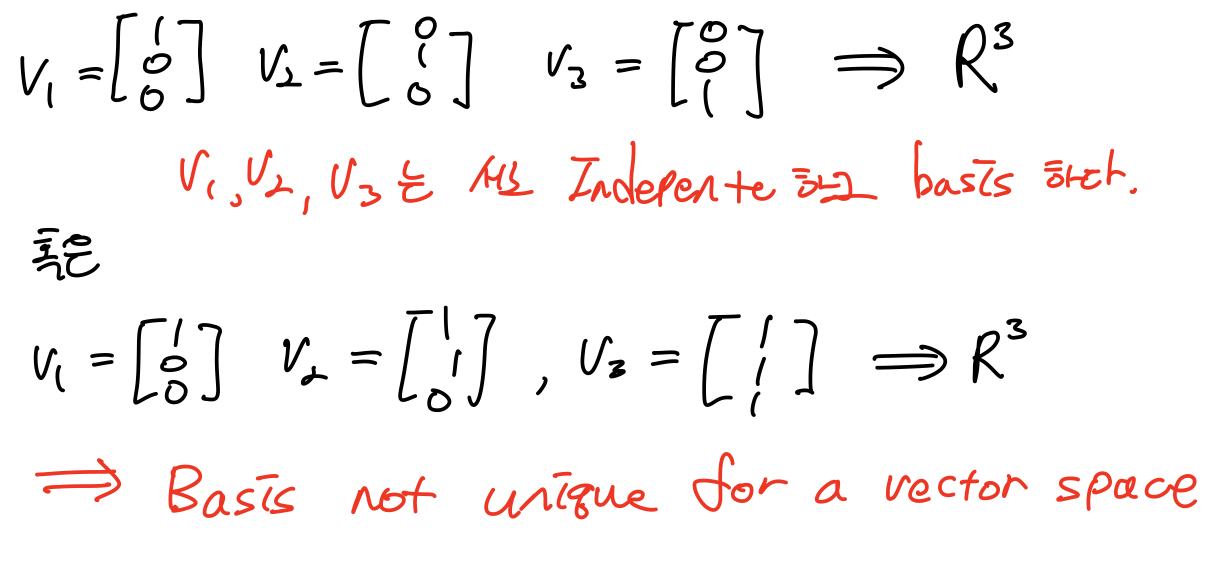
정리하면, vector space를 구성하는데 있어서 linearly independent한 basis vector가 주어있으면, 어떤 vector든 unique한 방법으로 linear combination을 표현할 수 있다.
근데 그 unique한 linear combination을 만들어낼 수 있는 basis vector는 vector space에 대해 unique하지 않다.
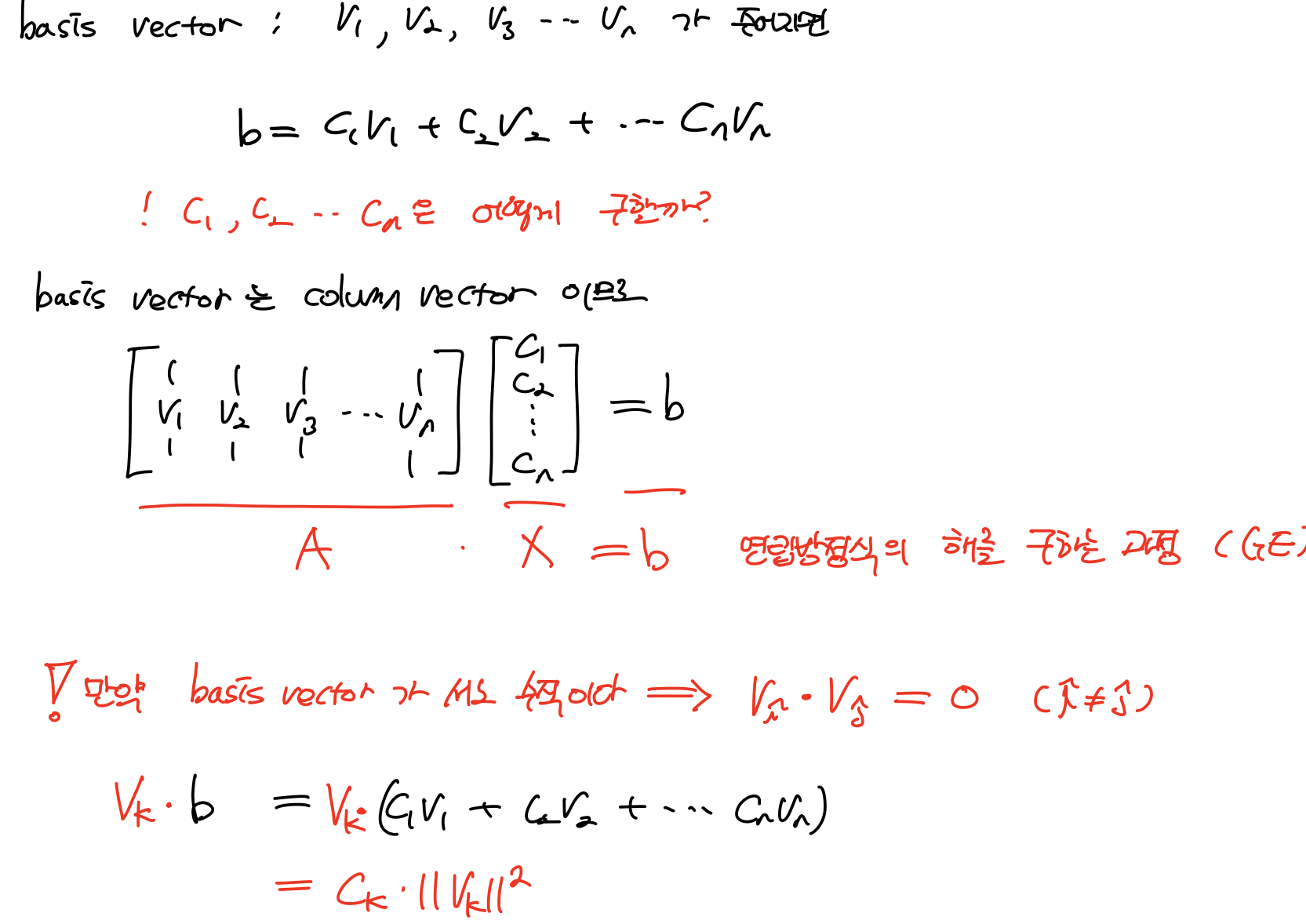
만약 basis vector가 서로 수직인 조건이 주어진다면, 위 사진에서 나타내는 것과 같이 우리는 상수 C를 바로 구할 수도 있다.
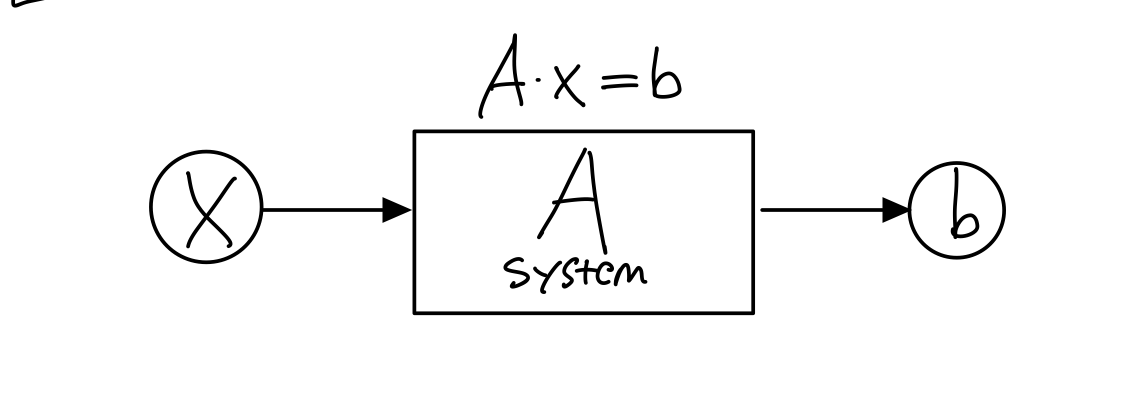
Ax=b에서 행렬 A를 system으로 볼 때, 여러 값을 가진 입력 X는 벡터구조이다. 그거로부터 출력 b로 본다면, A는 system을 동작을 나타내는 방법이 된다.
X를 알고 원하는 출력신호 b도 알고 있다면, 두 가지를 가지고 A를 알 수 있다. A를 설계하려면 A를 구성하는 column vector의 조합을 만들 수 있따. 이때 조건에 linearly independence 혹은 수직을 집어넣으면 X나 b를 쉽게 구할 수 있을 것이다.
1.4 Dimension of vector space
#number of linearly independente vectors
vector는 모양에 따라 Dimension의 자유도가 높지만, 실제 그 vector들을 가지고 만들 수 있는 조합의 Dimension은 높지 않을 수 있다.
1.5 Rank (r) of A
#number of independent column vectors
= # of independent row vectors
= # of pivots in GE
linearly independent한 column vector의 수이다. 이때 row vector또한 동일하다.
그리고 Gauss Elimination 했을 때 나오는 pivot의 수와 같다. 따라서 pivot이 나오는 column은 independent한 vector이다.
2. 4 fundamental Subspace in A

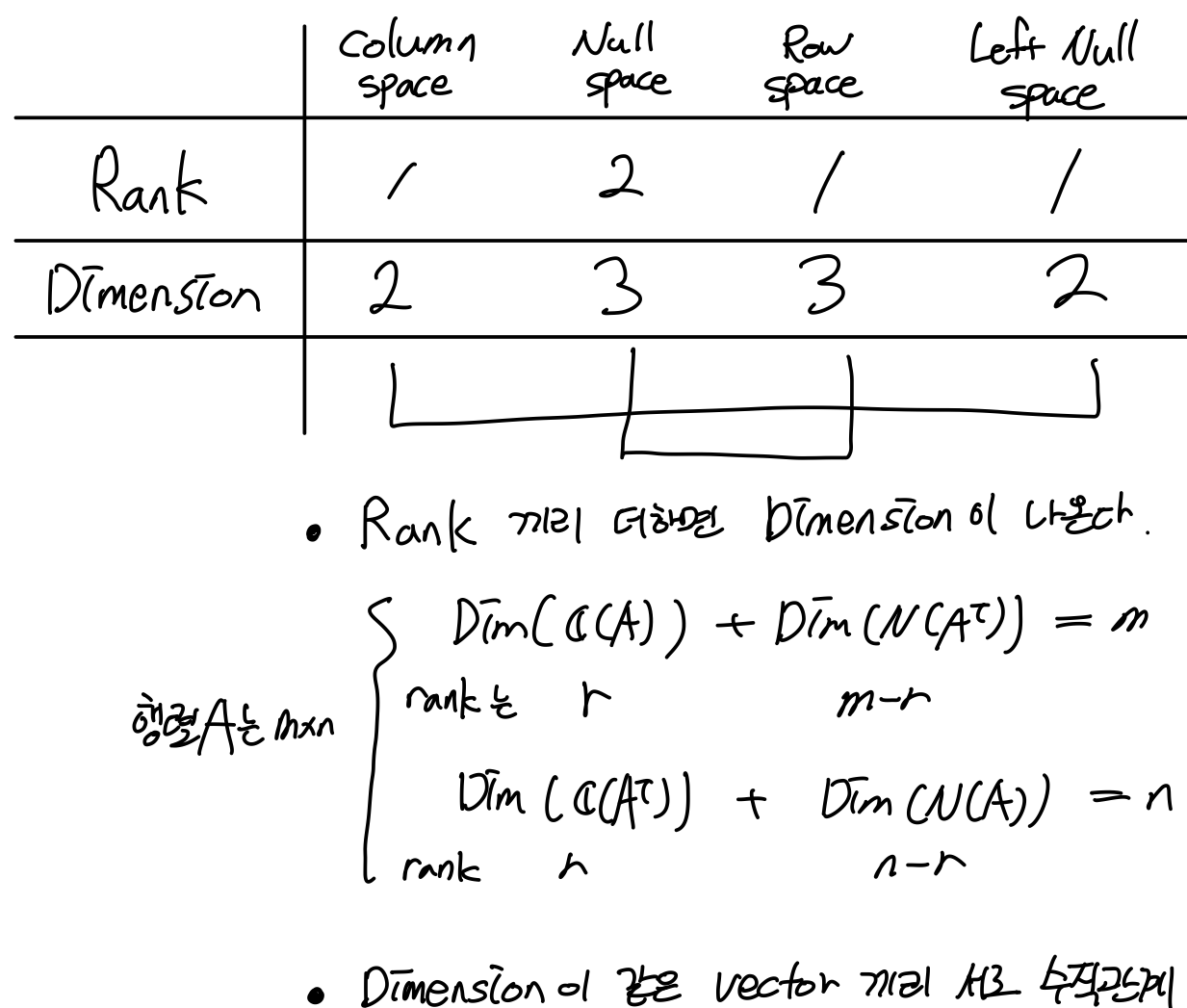
이때 행렬A를 m*n크기의 행렬이라 하면, vector X는 n차원이 된다. 따라서 Column space는 m차원 공간의 subspace가 되고, Null space는 반대로 n차원 vector space의 subspace가 된다.
또한, Row space는 행렬A의 Transpose 이니 Transpose A는 n*m크기의 행렬이 된다. 따라서 Row space는 n차원 공간이 된다. Left Null space는 m차원 공간이 된다.
예제를 보자.

자 여기서 개 신기한 점이 있다. Independent column vector의 수가 Rank(차원)이니까 각 space의 차원은 다음과 같다.
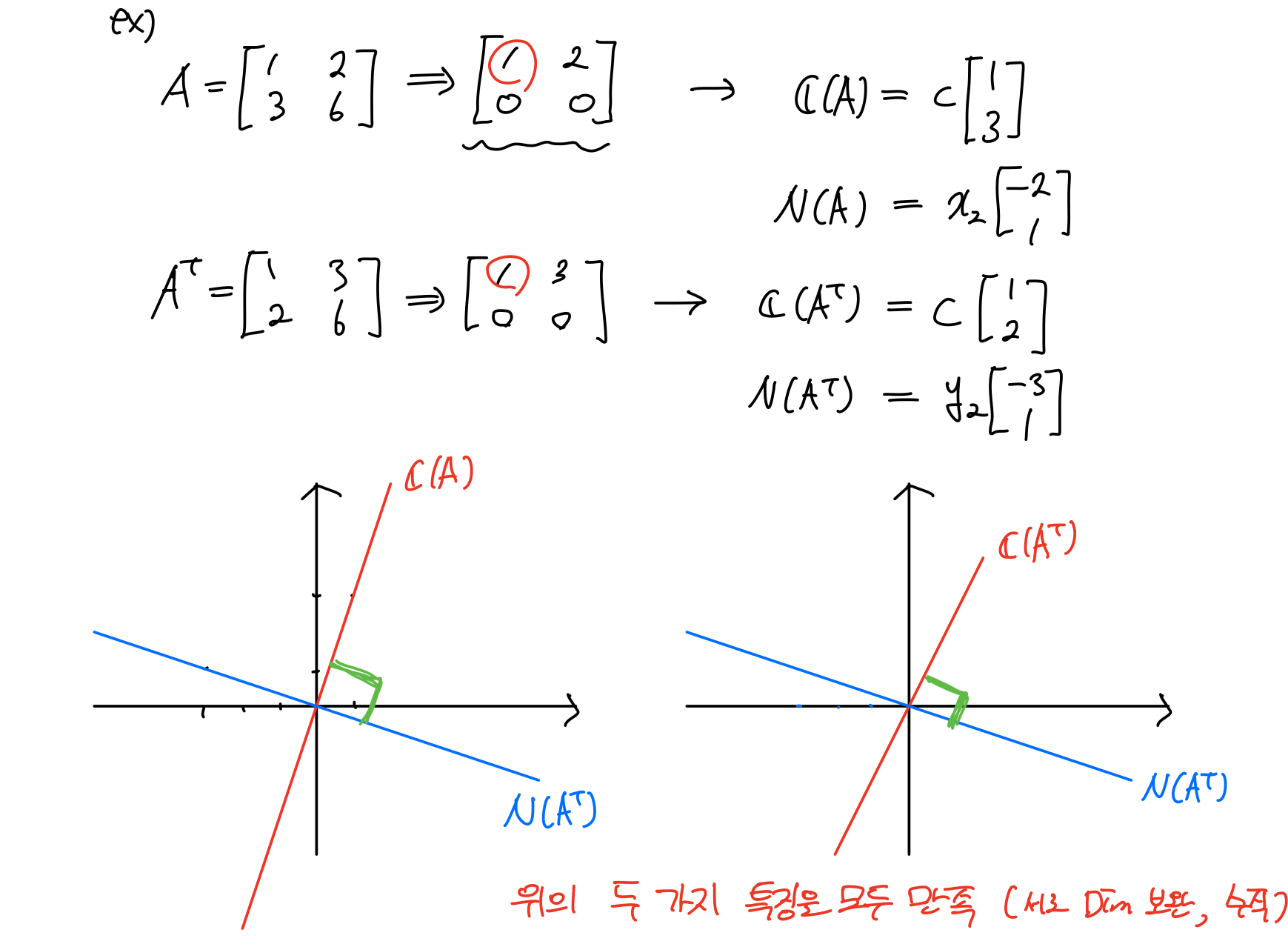
2.1 Existence of Inverses
Inverse Mat이 존재하는 3가지 경우는 아래와 같다. Square Mat과 Rectangular Mat.
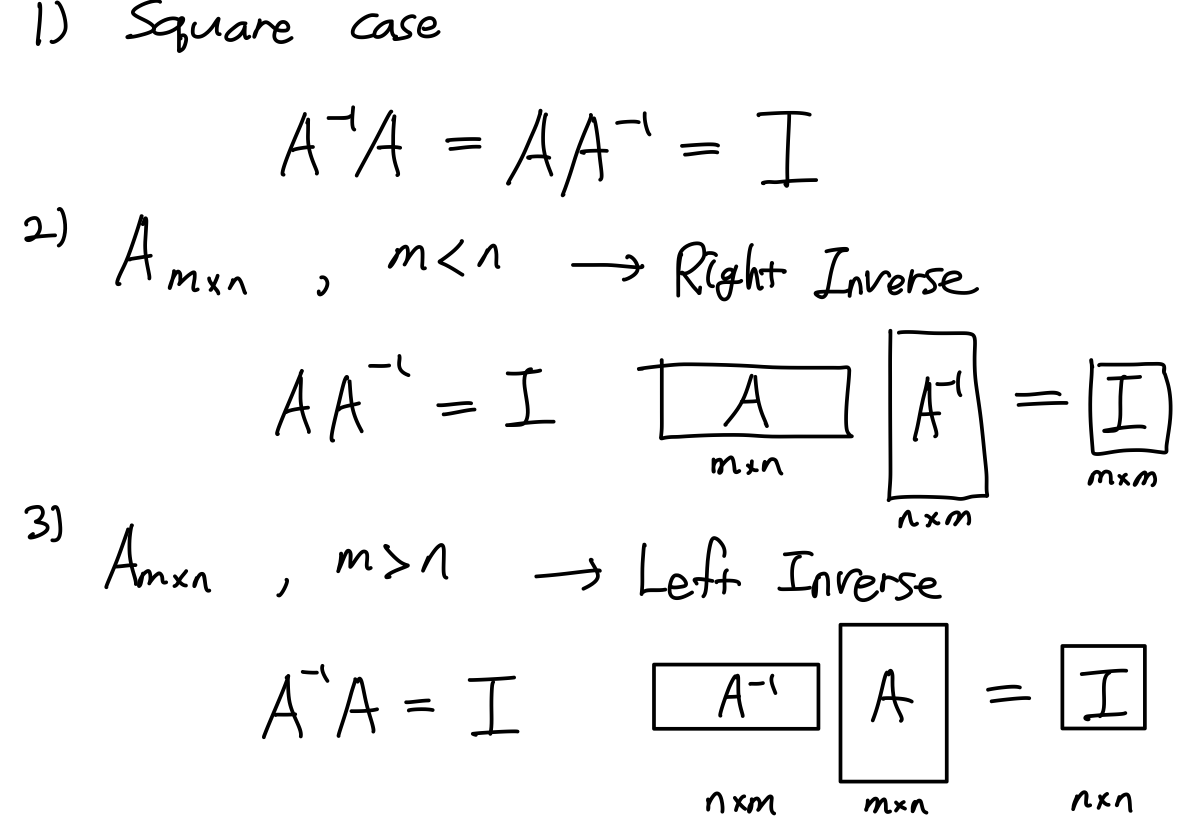
더 나아가, Left Inverse가 될 때와 Right Inverse가 될 때 Sol이 어떻게 되는지 살펴보자.

