8강_Exponential Dist & Erlang Dist

Eony_Jahng·2022년 1월 4일
확률과통계
0

확률과통계

목록 보기
8/10

"모두를 위한 열린 강좌 KOCW"에서 제공하는 한양대학교 이상화 교수님의 확률과통계 수업을 정리한 내용입니다.

Review

Poisson Dist

Number of Berronlli events in a time interval

포아송 확률분포는 단위시간 안에 어떤 사건이 몇 번 발생할 것인지를 표현하는 이산 확률분포(Discrete) 이다.

PX(x)=λxx!e−λ,x=0,1,2,...P_X(x)=\frac{\lambda^x}{x!}e^{-\lambda}, \quad x=0,1,2,...
E[X]=σX2=λE[X]=\sigma_X^2=\lambda

예를 들면 톨게이트나 은행 업무 중(단위 시간) 고객이 방문하는(events) 사건이 몇 번 발생하는가를 확률적으로 표현하는 것이다.

Exponential Dist

푸아송 확률분포가 이산적인 확률분포였다면, 지수 분포는 연속 확률분포이다. Random Variable X는 예로 lifetime 혹은 decaying time(방사성 동위원소의 반감기)를 들 수 있다.

연속적인 RV에 대한 확률분포를 나타내기에 확률 P를 정의할 수 없다. 따라서 PDF와 CDF를 활용해 표현하면 다음과 같다.

PDF: fX(x)=λe−λxPDF:\ f_X(x)=\lambda e^{-\lambda x}
CDF: FX(x)=∫0xλe−λtdt=1−e−λx=P(X≤x)CDF:\ F_X(x)=\int_{0}^{x}\lambda e^{-\lambda t}dt=1-e^{-\lambda x}=P(X\le x)
E[X]=1λE[X]=\frac{1}{\lambda}
σX2=1λ2\sigma_X^2=\frac{1}{\lambda^2}

또한, 지수 분포는 특징이 있다. 바로 forgetfulness(Memoryless)인데, 이는 현재부터 일어날 사건의 확률은 이전에 일어났던 사건과는 독립적임을 나타낸다. 즉, 지난 주에 로또번호가 안맞은 것이 이번주에 로또 맞을 확률과는 아무런 연관이 없다는거ㅎㅎ 그래서 안맞나보다...ㅎㅎ그래도 사야징~

consider a system has not failed by time t, then s>0 이면 최대 t+s 까지 생존할 확률에 t까지 생존할 확률은 전혀 영향을 미치지 않는다.

이를 수식으로 나타내면

P(X≤t+s∣X≥t)=P(X≤t+s∩X>t)P(X≥t)=P(t<X≤t+s)1−P(x≤t)P(X\le t+s | X \ge t)=\frac{P(X\le t+s \cap X>t)}{P(X\ge t)}=\frac{P(t<X\le t+s)}{1-P(x\le t)}

이를 CDF를 이용해 표현하면,

=FX(t+s)−FX(t)1−FX(t)=\frac{F_X(t+s)-F_X(t)}{1-F_X(t)}

이때 지수분포의 CDF FX(x)=1−e−λxF_X(x)=1-e^{-\lambda x}를 대입하면,

=e−λt−e−λ(t+s)e−λt=1−e−λs=FX(s)=\frac{e^{-\lambda t}-e^{-\lambda(t+s)}}{e^{-\lambda t}}=1-e^{-\lambda s}=F_X(s)

즉, t는 고려하지 않는 결과가 도출된다.

Relation E.D & P.D

continous RV를 다루는 Exponential Dist는 시간을 다루고, discrete RV를 다루는 Poisson Dist는 사건의 수를 다룬다. 그렇다면 이 두 확률분포 사이의 관계는 어떠할까~~?

for a poisson dist with λ\lambda per unit time

평균값 λ\lambda을 갖는 포아송 확률분포를 unit time 단위로 생각하면,

PX(x)=λxx!e−λ,x=0,1,2,...P_X(x)=\frac{\lambda^x}{x!}e^{-\lambda}, \quad x=0,1,2,...

그렇다면 unit time의 단위를 바꾸면 어떻게 될까?

for time unit interval t, λ→λt\lambda \rightarrow \lambda t

PX(x)=(λt)xx!e−λt,x=0,1,2,...P_X(x)=\frac{(\lambda t)^x}{x!}e^{-\lambda t}, \quad x=0,1,2,...

이를 활용해서 P.D가 E.D와 어떤 관계를 갖는지 파악해보자.

PX(X=0)=PX(no−event)=e−λtP_X(X=0)=P_X(no-event)=e^{-\lambda t}
PX(at least 1 event)=PX(X≥1)=1−PX(X=0)=1−e−λtP_X(at\ least\ 1\ event)=P_X(X\ge 1)=1-P_X(X=0)=1-e^{-\lambda t}

오케이...1−e−λt1-e^{-\lambda t} 어디서 봤다...!!!!! 바로 Exponential Dist의 CDF!! FX(x)=1−e−λxF_X(x)=1-e^{-\lambda x}이다. 이를 시간 t로 표현하면

FX(t)=1−e−λt=P(X≤t)F_X(t)=1-e^{-\lambda t}=P(X\le t)

결국

time interval between events →\rightarrow Exponential Dist를 따른다.
#of events in time interval →\rightarrow Poisson Dist

Erlang Dist

Erlang Dist is a generalization of Exponential Dist

어랑 분포는 지수 분포를 일반화시킨 확률분포이다. 이게 무슨 뜻인가 하면~ 우리는 위에서 다음 사건이 일어날 때까지 시간 간격은 지수분포를 따른다는 것을 알았다. 이것을 1개 시간 간격이 아닌, 2개 이상의 시간 간격을 묶어서 확률분포로 나타내는 것이 Erlang Dist이다.

따라서 RV은 다음과 같다.

Random Variable XkX_k: time interval of (k+1) successive events

K-order(Erlang-K) Dist는 다음의 특성을 갖는다.

PDF: fXk=λkxk−1(k−1)!e−λx,time x≥0PDF:\ f_{X_k}=\frac{\lambda^k x^{k-1}}{(k-1)!}e^{-\lambda x}, \quad time\ x\ge 0

당연히 k=1일 때는 Exponential Dist을 따른다.

CDF: FXk=∫0∞xλktk−1(k−1)!e−λtdt=1−∑j=0k−1(λx)je−λxj!CDF:\ F_{X_k}=\int_0^\infin x\frac{\lambda^k t^{k-1}}{(k-1)!}e^{-\lambda t}dt=1-\sum_{j=0}^{k-1}\frac{(\lambda x)^j e^{-\lambda x}}{j!}
E[Xk]=∫0∞xλkxk−1(k−1)!eλxdx=∫0∞(λx)ke−λx(k−1)!dxE[X_k] = \int_0^\infin x \frac{\lambda^k x^{k-1}}{(k-1)!}e^{\lambda x}dx=\int_0^\infin \frac{(\lambda x)^ke^{-\lambda x}}{(k-1)!}dx

이때 λx=u\lambda x=u, dudx=λ\frac{du}{dx}=\lambda이면,

=1λ∫0∞1(k−1)!uke−udu= \frac{1}{\lambda}\int_0^\infin \frac{1}{(k-1)!}u^k e^{-u}du

여기에서!!!! 새로운 개념이 필요하다. 바로 Gamma Function이라는 것인데, 이게 뭐냐면~

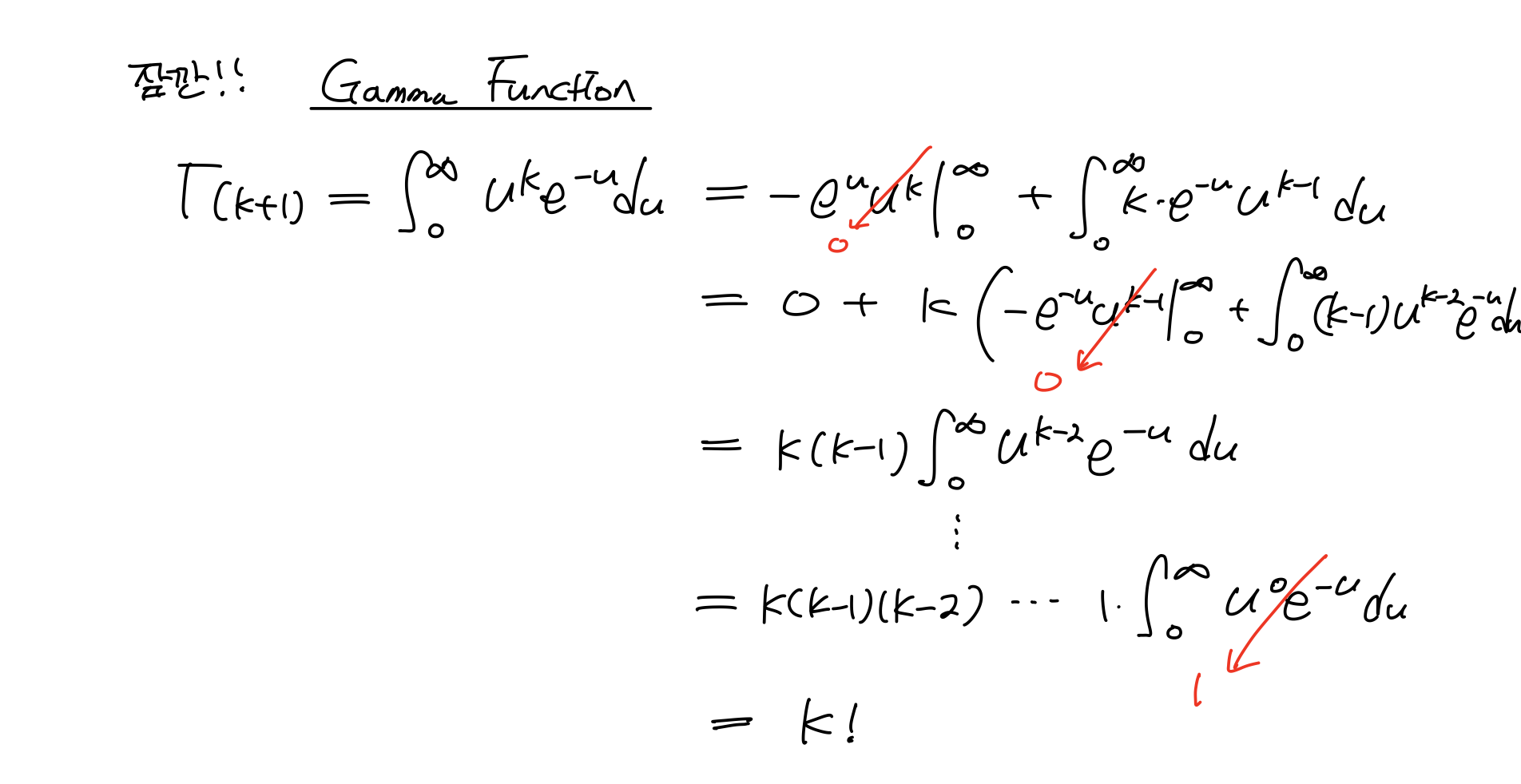
다시 Erlang Dist의 평균 E[X]을 구하면,

즉, Erlang Dist는 E.D 구간을 k개 더한 것의 확률분포이기 때문에 각 E.D의 E[X]=1λE[X]=\frac{1}{\lambda}을 k개 더한 값 kλ\frac{k}{\lambda}가 되는 것!!!! Wow~

그러면 분산은?? E.D의 분산 σX2=1λ2\sigma_X^2=\frac{1}{\lambda^2}이니 kλ2\frac{k}{\lambda^2}일까???

그렇다면 분산은

σX2=E[X2]−μ\sigma_X^2=E[X^2]-\mu

이므로

σX2=k(k+1)λ2−kλ=kλ2\sigma_X^2=\frac{k(k+1)}{\lambda^2}-\frac{k}{\lambda}=\frac{k}{\lambda^2}

두둥!!!! 예상한대로 나왔다ㅎㅎ확률은 참 어렵다가도 쉬운 학문인듯;;

Uniform Dist

profile
Eony_Jahng
7층에 사는 동언이
이전 포스트

7강_여러가지 이산확률분포

다음 포스트

9강_Normal Dist (Gaussian)

0개의 댓글

관련 채용 정보