Policy Gradients_Generalized Advantage Estimation _[CS285_HW2]

CS 285 Online Course at UC Berkeley의 Assingment2에 대한 내용입니다.

지금까지 살펴본 Advantage function을 살펴보면 다음과 같습니다.

critic의 advantage는 neural network baseline을 이용해서 variance를 낮출 수 있는 반면 bias는 높습니다. 그 이유는 만약 estimated value is wrong인 경우 즉, 학습이 올바르지 못한 경우는 bias가 증가하기 때문입니다.

샘플링된 데이터를 이용해 estimate하는 Monte Carlo의 경우 No bias이지만, single-sample estimation이기 때문에 Variance가 높다.

이 두가지를 적절하게 짬뽕해볼까?

step이 커질수록, time t가 커질수록 variance는 증가합니다. 그렇다면 target value의 step을 적절하게 설정하면 어떨까? n-step Monte Carlo return을 적용하면 다음과 같다.

n-step Monte Carlo Return을 이용한 Advantage Estimation

n -step Monte Carlo 반환을 사용하여 Advantage 추정을 수행하는데, 여기서 n값을 조정하여 추정의 편향과 분산 사이의 균형을 조절할 수 있습니다. n이 증가할수록 편향은 감소하고 분산은 증가합니다. 이와 함께, n-step Advantage 추정치를 지수 가중 평균으로 결합하여 Generalized Advantage Estimator (GAE)를 형성하고, $\lambda$ 파라미터를 통해 편향과 분산의 균형을 조절할 수 있게 합니다.

Generalized Advantage Estimator (GAE)

$\lambda$가 높을수록 높은 n에 더 큰 가중치를 두어 분산을 증가시키고 편향을 감소시키며, GAE는 재귀적으로 계산될 수 있어 효율적인 구현이 가능합니다. 이러한 계산 방법은 강화 학습 알고리즘의 성능을 최적화하는 데 중요한 도구로 사용됩니다.

see the GAE paper

Generalized Advantage Estimator (GAE) for Infinite Horizon

$A_{GAE}^\pi(s_t, a_t) = \frac{1}{1 - \lambda} \sum_{n=1}^\infty \lambda^{n-1} A_n^\pi(s_t, a_t) = \sum_{t'=t}^\infty (\gamma \lambda)^{t'-t} \delta_{t'}$

Generalized Advantage Estimator (GAE) for Finite Horizon

$A_{GAE}^\pi(s_t, a_t) = \sum_{t'=t}^{T-1} (\gamma \lambda)^{t'-t} \delta_{t'}$

Recursive Computation of GAE

$A_{GAE}^\pi(s_t, a_t) = \delta_t + \gamma \lambda A_{GAE}^\pi(s_{t+1}, a_{t+1})$

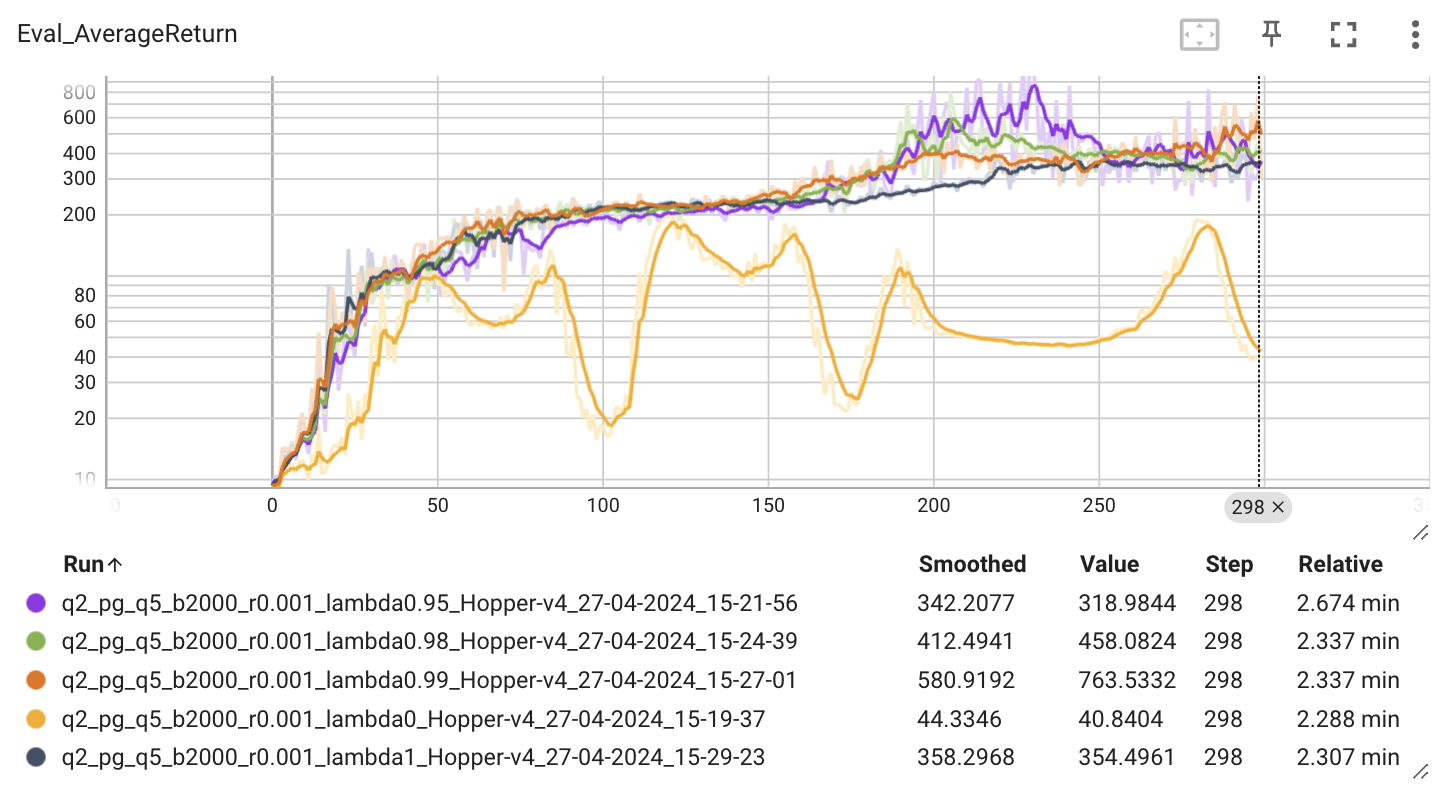
Hopper-v4 환경에서 $\lambda$를 [0, 0.95, 0.98, 0.99, 1]로 실험한 결과 0.99일 때 가장 높은 Return를 보여주는 것을 확인할 수 있습니다.