3차원 선형 변환 | Chapter 5, Essence of Linear Algebra [3Blue1Brown]

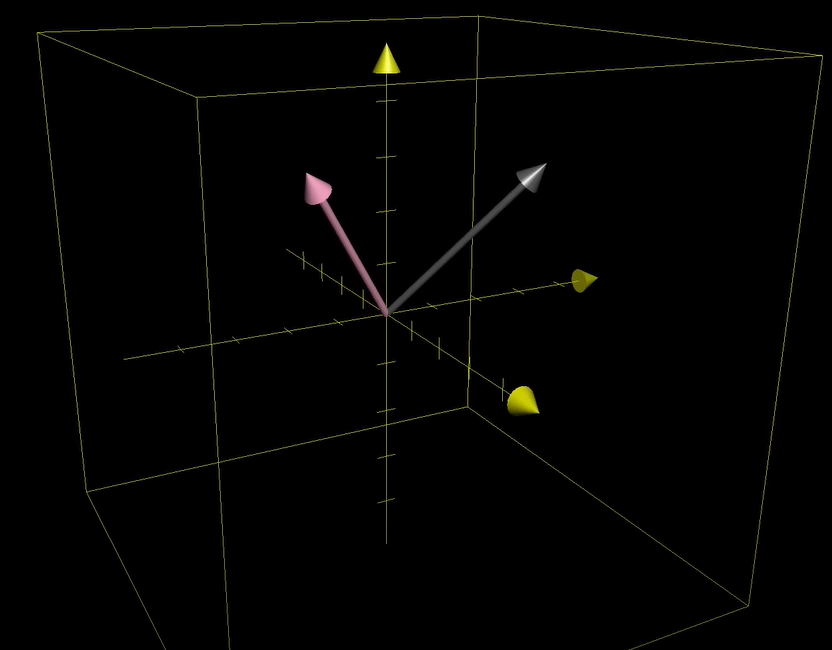
Comment :

챕터1,2,3,4를 통해 무엇을 배웠는가...

• ✅ Chapter 1 : 벡터 / 하나의 움직임 하나의 단계로 보는 벡터의 합 / Scalar값을 통한 벡터를 늘리고 줄이고 뒤집는 Scaling
• ✅ Chapter 2 : 벡터가 존재하는 공간의 좌표계를 정하는 기저벡터 / 두 (기저) 벡터를 Scaling하고 더하는 선형 변환(Linear Transformation) / 선형조합(Linear Combination)으로 나타낼 수 있는 벡터의 집합, Span
• ✅ Chapter 3 : 벡터공간 좌표계의 변화적 움직임때문에 (함수가 아닌) 선형 변환으로 불림 / 선형변환은 기저벡터의 변환이다! / 행렬, 즉 Matrix를 기저벡터 한 쌍으로 보는 관점
• ✅ Chapter 4 : 선형 변환과 Matrix / 여러번의 선형변환과 Matrix 간 곱셈

01. 3차원 선형 변환

[!] 이번 챕터(Chapter 5; 3차원 선형변환)의 경우 지금까지 배웠던 것을 3차원 관점으로 확대해보는 정도로 생각하면 된다.

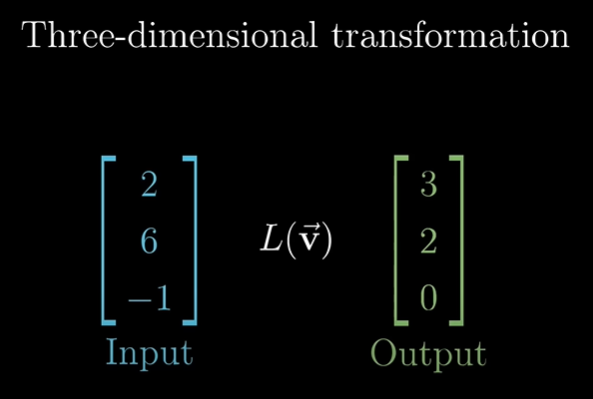
앞서 학습하였던 2차원의 선형 변환(Linear Transformation)과 똑같이 3차원의 선형 변환의 경우도 3차원의 벡터를 입력하여 3차원의 벡터를 출력받는다.

또한 2차원의 선형 변환(Linear Transformation)과 똑같이 3차원의 선형 변환의 경우도 3차원 격자(Grid)가 평행, 간격 일정, 원점은 고정되어 있다.

또한 2차원의 선형 변환(Linear Transformation)과 똑같이 3차원의 선형 변환의 경우도 (변환 이후, 또는 변환할) 기저벡터*만 알고 있으면 변환을 할 수 있다. 즉 아래처럼 총 9개의 값을 알면 된다.

• x축 : $\hat{i}=[?,?,?]$
• y축 : $\hat{j}=[?,?,?]$
• z축 : $\hat{k}=[?,?,?]$

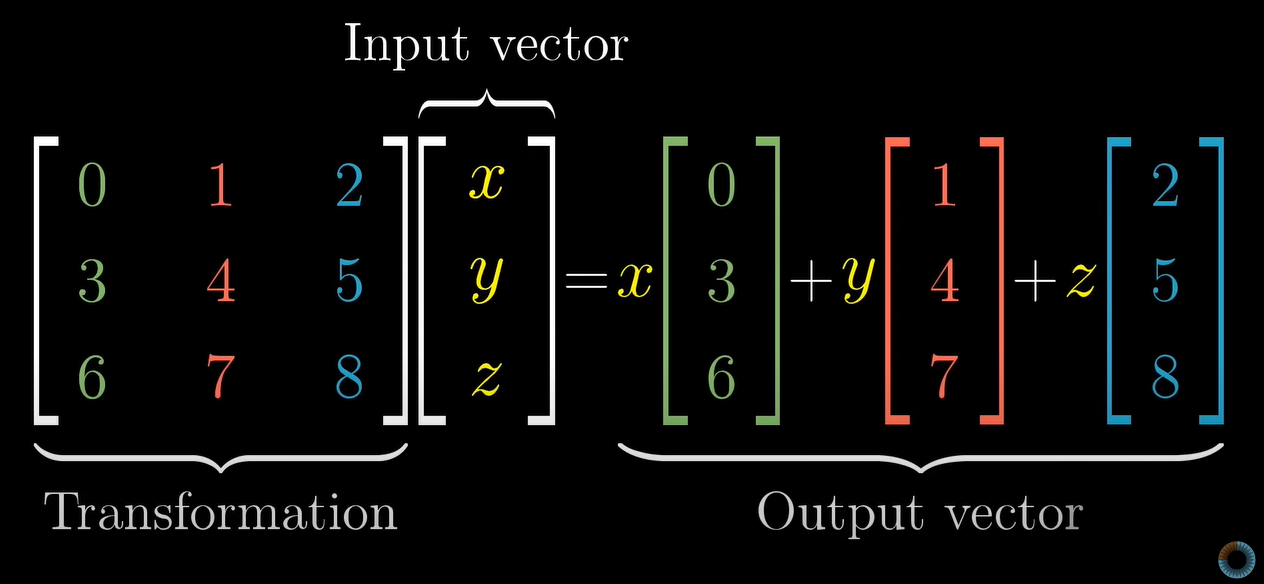
(2차원 선형변환과 동일하게) 변환된or될 기저벡터 3개에 각각의 Scaling 이후 더해주면 Transformation이 완료된 Output 벡터를 알 수 있음.

아래와 같은 수식에서 $\hat{i}, \hat{j}, \hat{k}$ 만 알면 된다.

$\vec{v} = \begin{bmatrix} x \\ y \\ z \end{bmatrix} = x\hat{i}+y\hat{j}+z\hat{k}$

---

02. 여러번의 3차원 선형변환

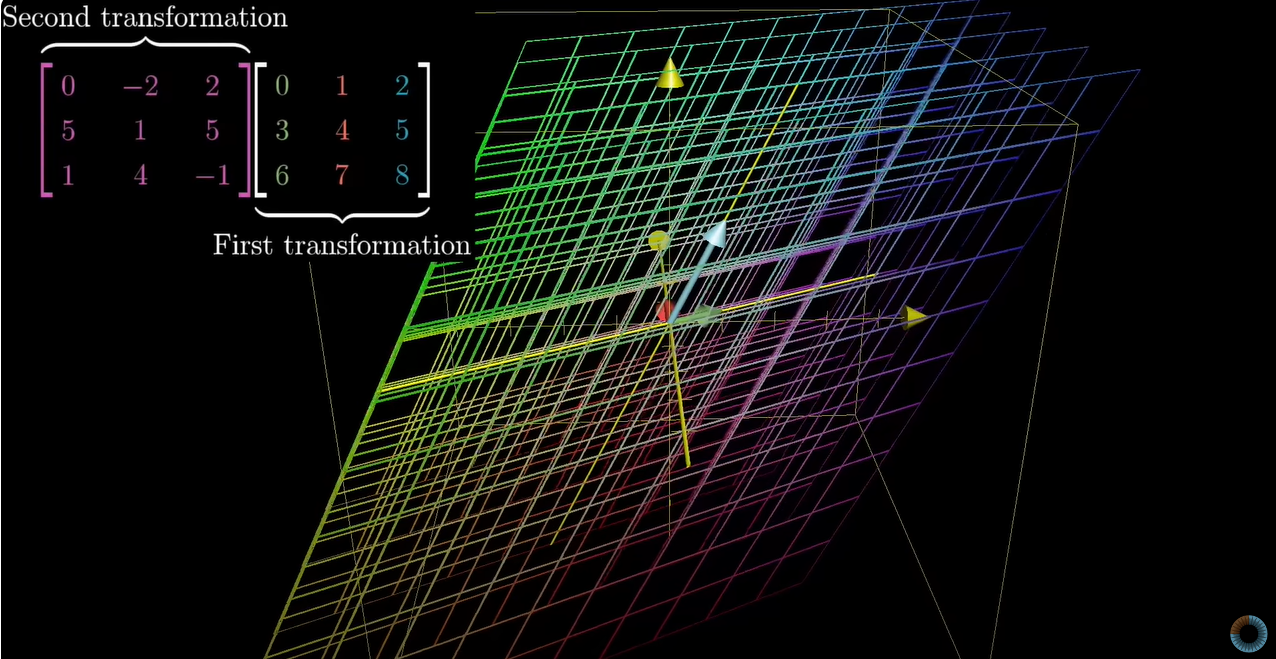
앞서 학습하였던 여러번의 2차원 선형변환(Linear Transformation)과 동일하게 3차원 선형변환 또한 아래 그림과 같이 단계별로 변환을 진행하면 된다.
[+] Computer Graphics, Robotics 분야에서 3차원에서의 회전을 Description하기 어려웠으나 작은 변환들로 쪼개고 그것의 결합, 즉 Composition으로 생각하면 회전을 다루기 쉬워진다.

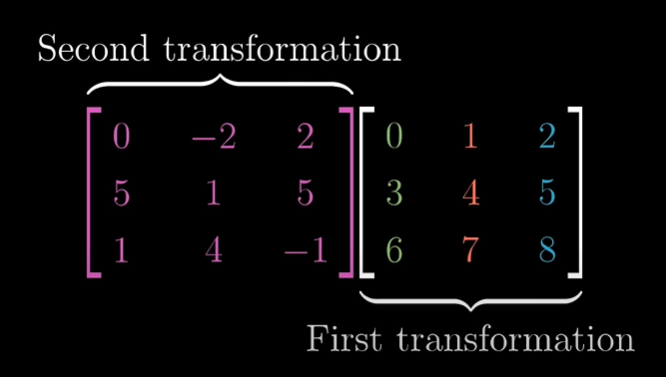
수식적으로 3차원 선형변환을 계산하는 방법 또한 2차원 선형변환과 동일하다. 복습 겸 아래의 1차 2차 Transformation을 2가지 방법(행렬 곱셈법, 기저벡터의 선형변환)으로 풀어보자.