Vectors | Chapter 1, Essence of Linear Algebra [3Blue1Brown]

Chapter 1, Essence of Linear Algebra

---

01. 벡터, 그리고 벡터의 표현

선형대수학, 즉 Linear Algebra에서의 근본적인 구성 조각(본질, 기초?)은 바로 벡터이다. 이 벡터를 바라보는 관점은 3가지가 있다고 볼 수 있다.

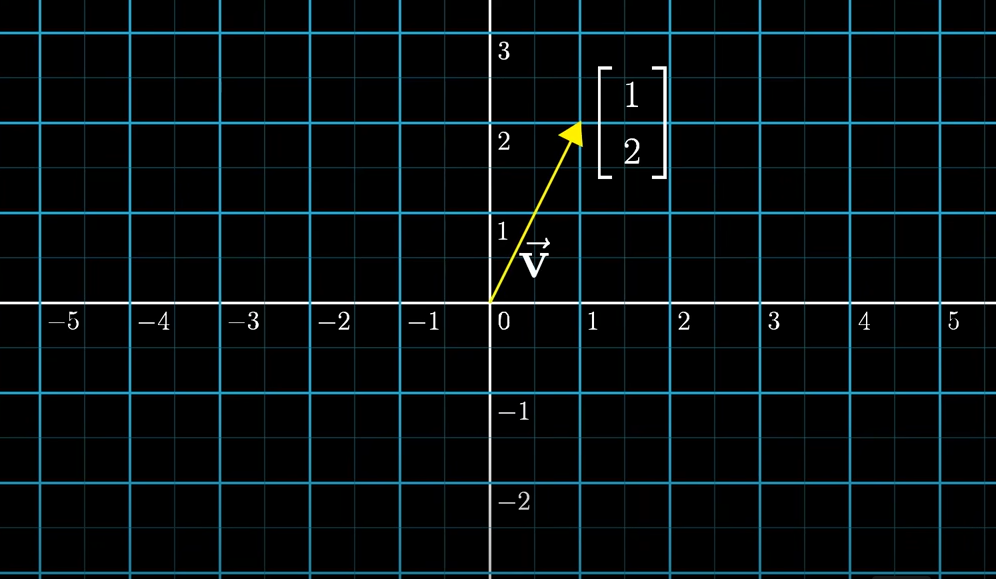
1. Physics👩‍🚀 : 벡터는 공간에서의 화살표, 이 화살표의 길이와 방향이 같다면 공간 어디에 있든 모두 같은 벡터 벡터의 원점이 꼭 0,0일 필요가 없는...?

2. Computer Science👩‍💻 : 벡터는 순차적인 숫자 리스트 순서가 있는 나열된 숫자

3. Mathematic 🧙‍♂️ : 상수배, 벡터간 합 등이 적용되는 모든 것 다소 추상적인 모든 것
   
   
   
   

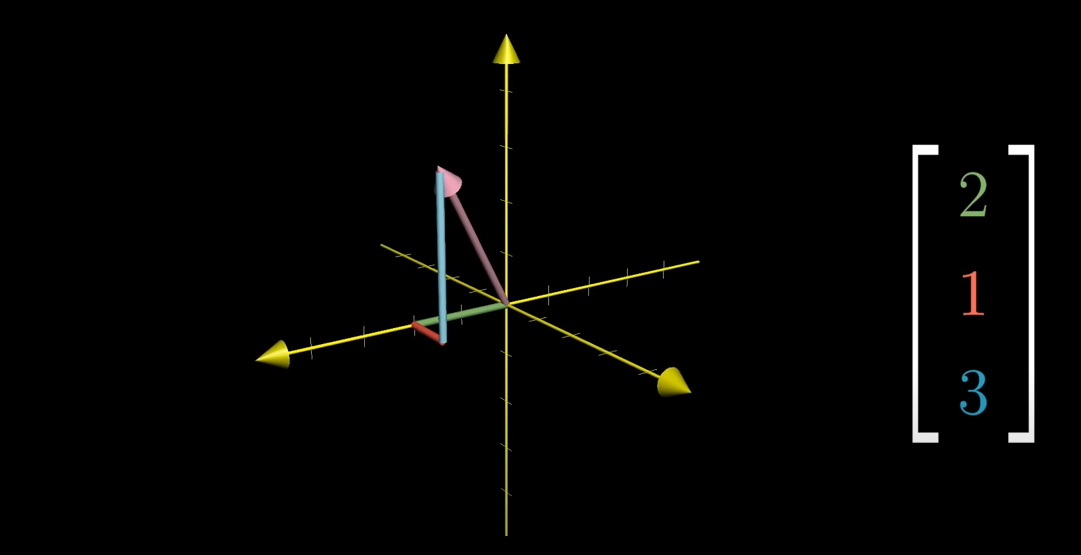
선형대수학을 학습하기 위하여 위 그림과 같은 Normal한 좌표계(노란색)를 기준으로 벡터를 생각하자. 우측에 나열된 숫자와 같이 x축 기준 2, y축 기준 1, z축 기준 3 칸 이동하면 아래의 벡터를 표현하는 것이다.

당연히 2차원 벡터의 경우 2개의 숫자가 나열된 리스트로 표현할 수 있다.

[+] 내가 관찰하는 대상이 '집'이고 '집'에 대한 면적, 가격을 알 수 있다고 생각해보자. 이때 어떤 '집'을 2차원 벡터로 모델링, 즉 표현할 경우 아래와 같다.

---

02. 벡터 합

선형대수의 모든 주제는 다행히도? 벡터의 합과 상수배(=숫자곱), 두가지 연산을 중심으로 일어난다.

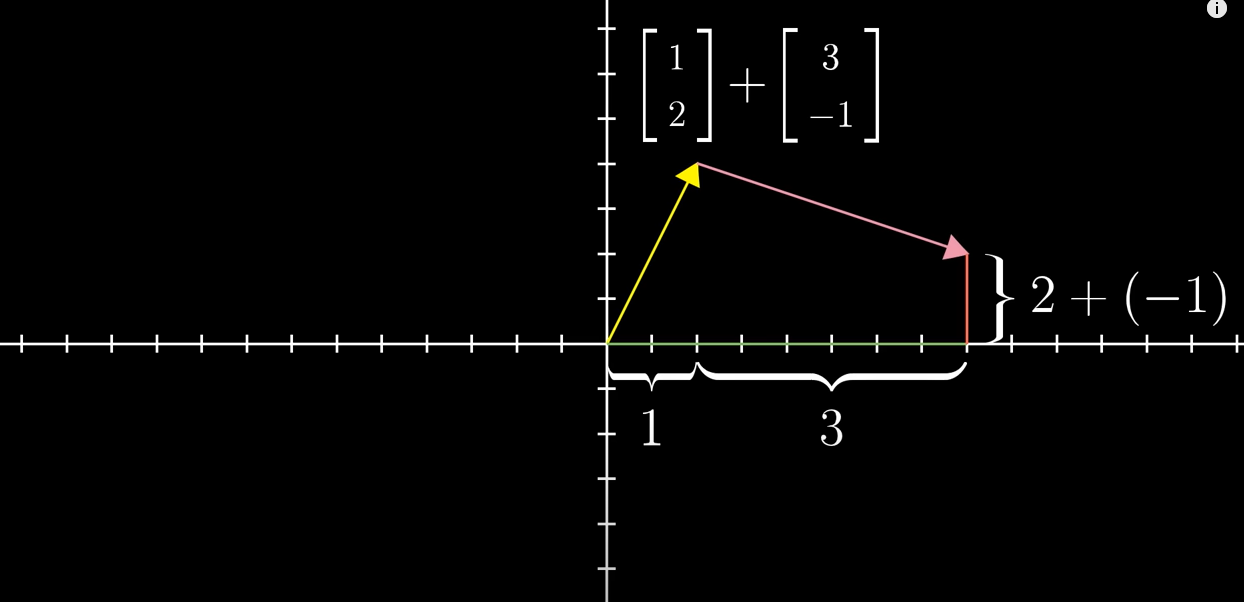
위 이미지처럼 기하학적인 벡터의 합은 첫번째 벡터의 끝에 두번째 벡터를 이동시켜서 두번째 벡터가 가리키는 부분이 두 벡터의 합이 된다. (왜 원점에서 시작하는 두 벡터의 합 연산 시 한개의 벡터를 이동시켜야 되는것일까?) 이는 벡터는 하나의 움직임, 그리고 하나의 단계로 볼 수 있기 때문이다. 따라서 위 그림과 같은 두 벡터의 합에서는 아래와 같은 단계의 움직임이 된다고 볼 수 있다.

1. 첫번째 벡터의 움직임 또는 단계
   • x축 방향으로 +1만큼 이동
   • y축 방향으로 +2만큼 이동
2. 두번째 벡터의 움직임 또는 단계
   • x축 방향으로 +3만큼 이동
   • y축 방향으로 -1만큼 이동

위와 같은 단계의 움직임은 (x축과 y축은 독립적이므로?, 서로 영향을 주지 않으므로) x축 방향의 움직임부터 진행하고, y축 방향의 움직임을 진행하여도 같은 결과임을 알 수 있다. 고로... 두 벡터의 합은 아래와 같이 계산할 수 있다.

---

03. 숫자곱(상수배)

(벡터 합 외의 선형대수에서의 Fundamental한 연산은) Multiplication by a Number, 즉 숫자곱이 있다.

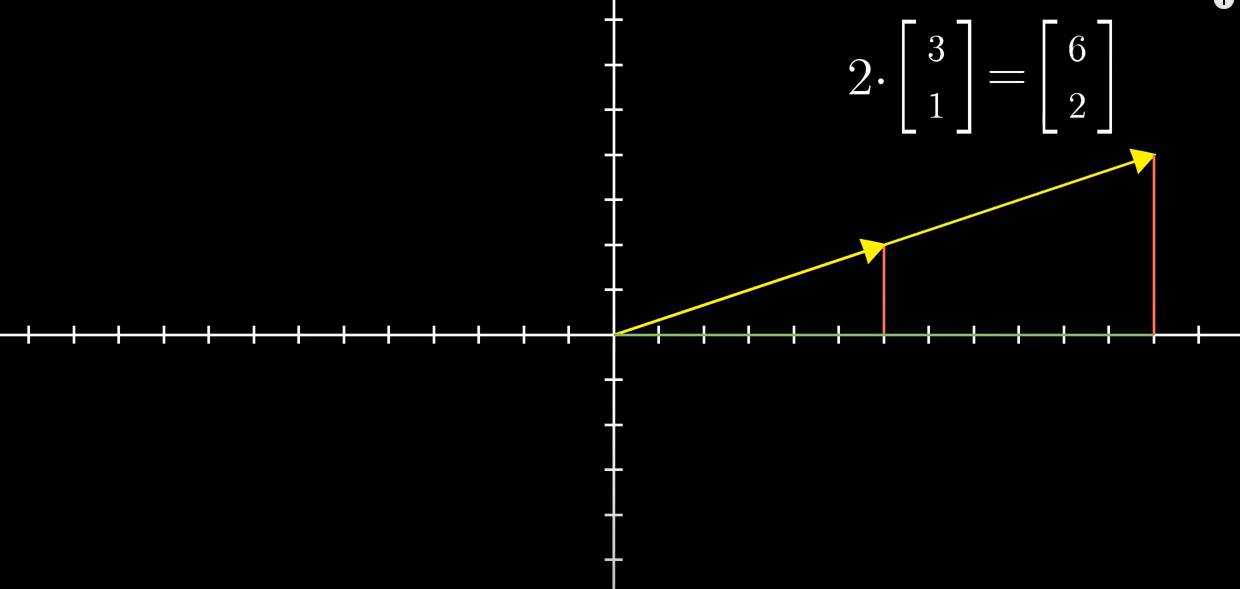
🔰 벡터 스케일링(Vector Scaling)

벡터를 늘리고 줄이고 뒤집는 것, 그 벡터의 방향이 바뀌면 안된다(역방향 제외)
또한 어떤 벡터를 늘리고 줄이는 '정도'를 Scalar라고 한다.

(벡터가 존재하는 방향축에서 벗어나지 않는 한에서) 벡터를 어떤 '정도'만큼 늘리고 줄이는 것을 아래와 같이 표현할 수 있다.

여기서 $c$가 바로 벡터를 어느정도 Scaling하는지에 대한 정도인 Scalar이며, 계산을 아래과 같이 할 수 있다.