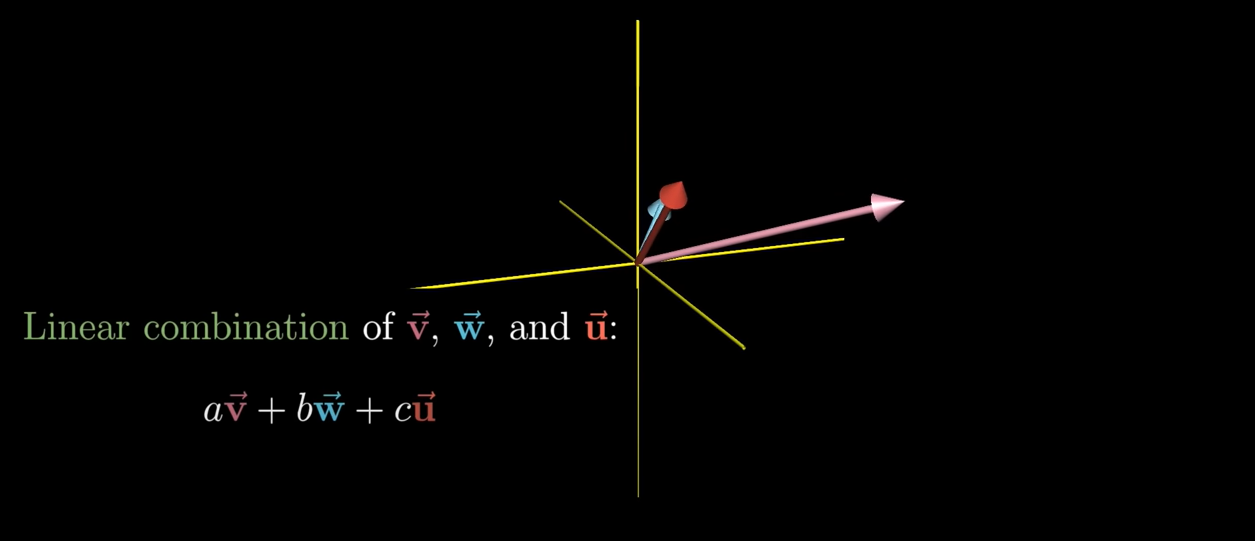선형 조합, 범위 및 기저 벡터 | Chapter 2, Essence of Linear Algebra [3Blue1Brown]

olxtar·2024년 2월 5일
3Blue1BrownLinear Algebra
0

[3Blue1Brown] Essence of Linear Algebra

목록 보기
2/5

Comment :

이전 Chapter에서는 '벡터'에 대해서 알아보았다. 벡터라는 것은 (몇개의 관점에서 바라볼 수 있지만) 아래와 같이 순서대로 나열된 리스트라고 볼 수 있다.

x⃗=[abc]\vec{x} = \begin{bmatrix} a \\ b \\ c \end{bmatrix}

🔰 벡터간의 합은 각 독립적인 축으로의 합으로 생각할 수 있으므로 아래와 같이 계산된다.

a⃗+b⃗=[abc]+[def]=[a+db+ec+f]\vec{a}+\vec{b} = \begin{bmatrix} a \\ b \\ c \end{bmatrix} + \begin{bmatrix} d \\ e \\ f \end{bmatrix} = \begin{bmatrix} a+d \\ b+e \\ c+f \end{bmatrix}

🔰 벡터의 상수배는 Scalar Multiflication, 즉 Scaling으로도 불린다.

c⋅v⃗c \cdot \vec{v}

여기서 cc가 바로 벡터를 어느정도 Scaling하는지에 대한 정도인 Scalar이며, 계산을 아래과 같이 할 수 있다.

c⋅[xy]=[c⋅xc⋅y]c \cdot \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} c \cdot x \\ c \cdot y \end{bmatrix}




01. 기저 벡터

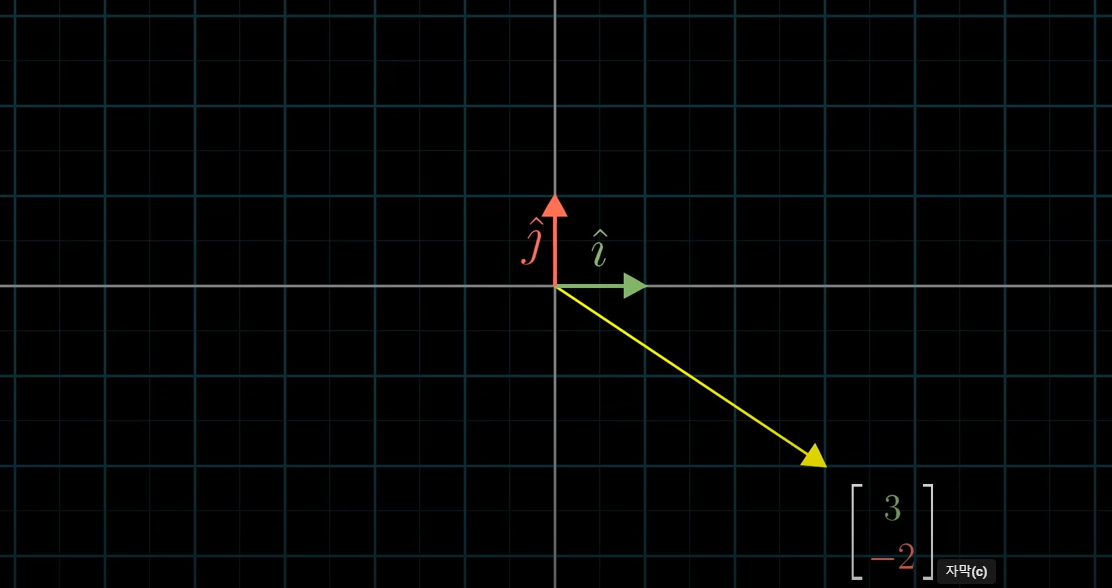
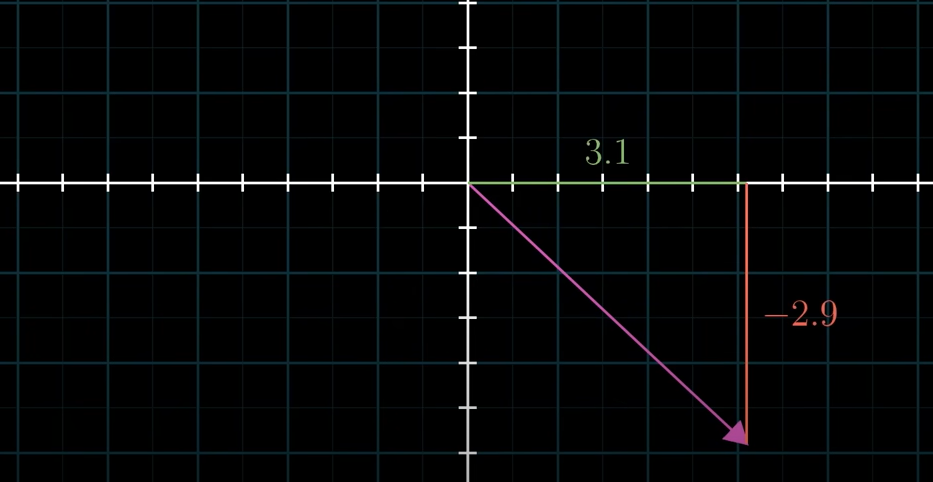
우리는 아래와 같은 벡터를 그려보라고 할때 (너무나도 당연하게) x-y 직좌표계(x-y coordinate system)에 각각의 숫자 (3,-2)만큼 x축, y축으로 늘어난 화살표를 그린다.


v⃗=[3−2]\vec{v} = \begin{bmatrix} 3 \\ -2 \end{bmatrix}

이때

i^=[10],    j^=[01]\hat{i} = \begin{bmatrix} 1 \\ 0 \end{bmatrix}, \space\space\space\space \hat{j} = \begin{bmatrix} 0 \\ 1 \end{bmatrix}

위와 같은 두 벡터를 생각해보자. 그러면 v⃗\vec{v}는 다시 아래와 같이 나타낼 수 있다.


v⃗=3⋅[10]+−2⋅[01]=[30]+[0−2]=[3−2]\vec{v} = 3\cdot \begin{bmatrix} 1 \\ 0 \end{bmatrix} + -2 \cdot \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 3 \\ 0 \end{bmatrix} + \begin{bmatrix} 0 \\ -2 \end{bmatrix} = \begin{bmatrix} 3 \\ -2 \end{bmatrix}

∴v⃗=3i^+−2j^(1)\therefore \vec{v} = 3 \hat{i} + -2 \hat{j} \tag{1}

(1) 수식처럼 벡터는 어떠한 벡터들을 상수배하고 서로 더한 결과라고 볼 수 있다. 저 어떠한 벡터(i^,j^\hat{i}, \hat{j})를 orthogonal(x-y) coordinate system의 basis vectors(직교 x-y 좌표계의 기저벡터)라고 한다.

(뭐 이렇게 쪼개서 계산하나 생각이 들지만) 사실 우리는 암묵적으로 저 i^,j^\hat{i}, \hat{j} 벡터로 구성되는 좌표계를 사용한다는 것이다.


v⃗=[ab]\vec{v} = \begin{bmatrix} a \\ b \end{bmatrix}

위와 같은 벡터 v⃗\vec{v}에서 우리는 바로 aa, bb라는 Sclar값을 x,yx,y축에서의 값으로 인식하는데...
이는 곧 a,ba, b라는 Sclar값을 통해 i^,j^\hat{i}, \hat{j}라는 basis vector를 스케일링하는 것이다.

"다시 말해 좌표계를 2개의 기저벡터로 구성하는 것"



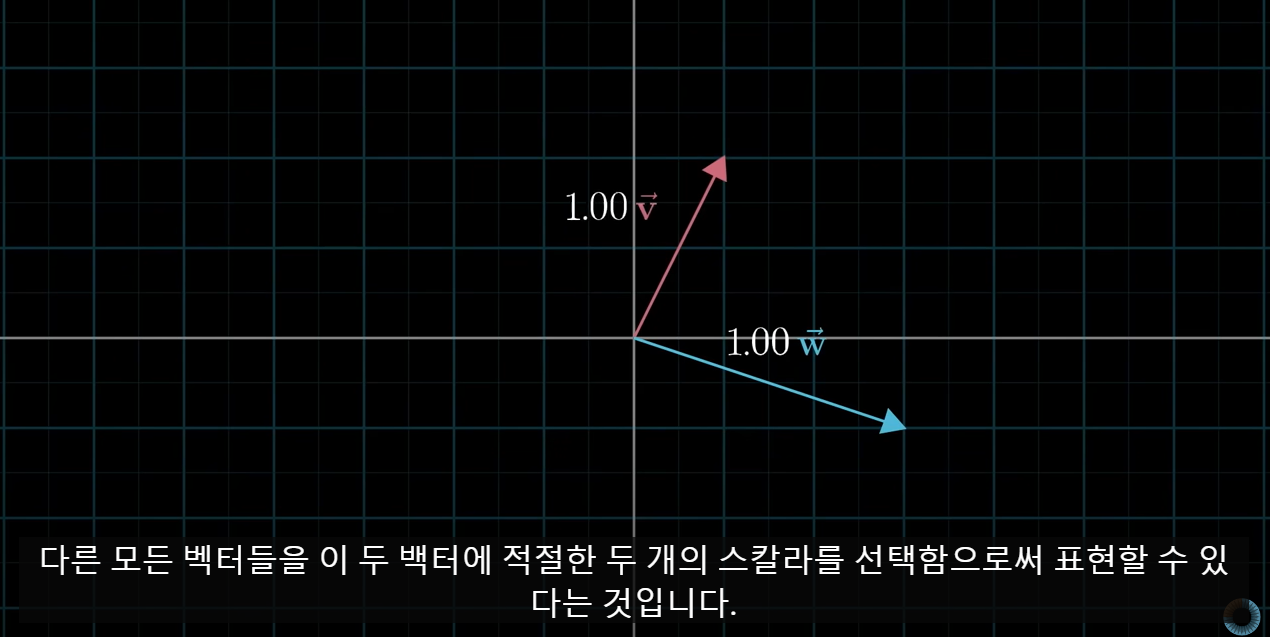
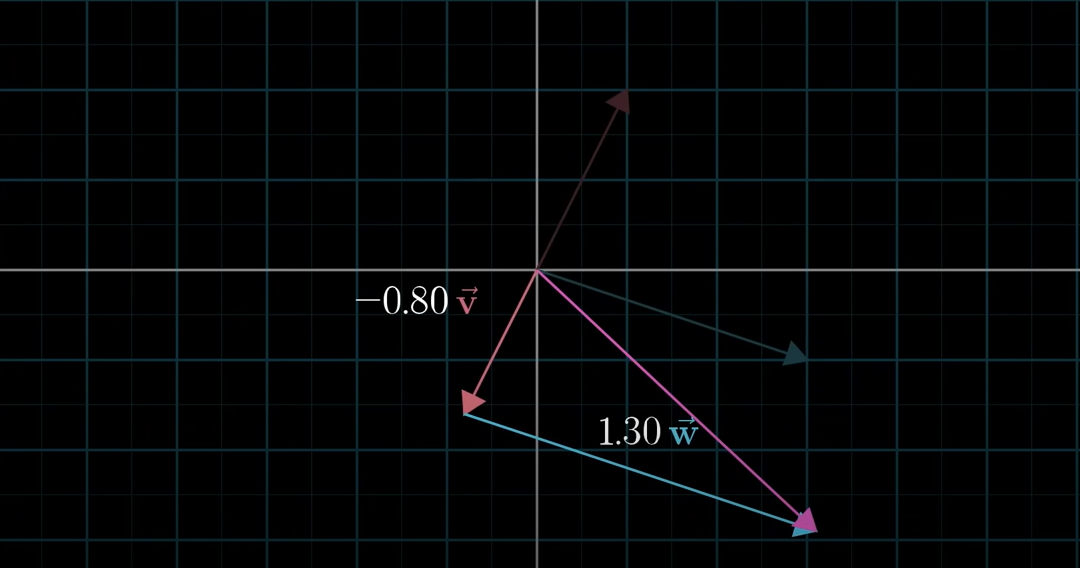
따라서 우리가 만약 다른 기저벡터(위 그림처럼 v^,w^)\hat{v}, \hat{w})를 선택한다면, 완전히 다른 좌표계를 생각할 수 있을 것이다. 하지만 다른 모든 벡터들을 이 두 기저벡터 (v^,w^\hat{v}, \hat{w})와 스칼라의 조합으로 표현할 수 있다.


위 2개 이미지에서의 보라색 벡터는 (같은 벡터이지만) 아래와 같이 두가지 방법으로 나타낼 수 있다.

−0.80v⃗+1.30w⃗(2)-0.80 \vec{v} + 1.30 \vec{w} \tag{2}
3.1i⃗+−2.9j⃗(3)3.1 \vec{i} + -2.9 \vec{j} \tag{3}

또한 (3) 수식의 경우 아래와 같이 단순하게 표현(한다...)할 수 있다. (물론 (2)수식또한 단순 숫자리스트로 표현이 가능하나 기저벡터의 특이함때문에 언급을 해줘야할것이다) 아래와 같이 특정 기저벡터를 표현하지 않음으로써 우리는 단순 숫자 리스트로 벡터를 표현 시 암묵적으로 특정 기저벡터를 선택하였다는 것을 보여준다.


[3.1−2.9](3-a)\begin{bmatrix} 3.1 \\ -2.9 \end{bmatrix} \tag{3-a}




02. 선형 조합

두 벡터를 Scaling하고나서 더하는 것... 다시 말해서 (두개의 기저) 벡터를 Scalar Multiplication한 뒤 합하는 것을 두 벡터의 선형 조합(Linear Combination)이라고 한다.

💫 Linear Combination of v⃗\vec{v} and w⃗\vec{w} (a,b는 Scalar값)

av⃗+bw⃗a \vec{v} + b \vec{w}




03. span

"The span of v⃗\vec{v} and w⃗\vec{w} is the set of all their linear combinations."

주어진 두 벡터(v⃗\vec{v}, w⃗\vec{w})의 선형조합(Linear Combination)으로 나타낼 수 있는 결과 벡터들의 집합을 두 벡터의 span이라고 한다.

두 벡터의 span은 아래와 같이 묻는것과 같다. 오직 (두 벡터의) 벡터합, 그리고 스칼라곱 연산만을 가지고서 도달 가능한 벡터들의 집합은 어떠한가?

아마 위 그림처럼 어떠한 '면'이 될 것이다. (두 벡터의 선형결합으로 생성되는 벡터, 즉 위그림에서 하늘색 벡터를 화살표로 보지말고 하나의 점으로 생각해보자. 그러면 두 기저벡터가 자유롭게 변함에따라 하늘색 벡터의 끝 점은 위 그림과 같은 평면 어디에든 존재 가능하다)



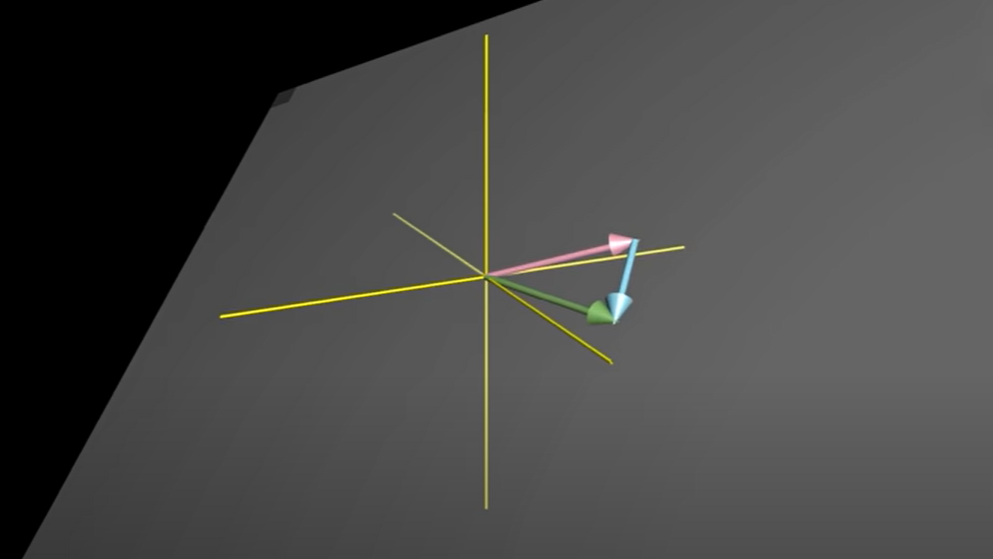
그러면 3개의 벡터의 선형조합으로 나타낼 수 있는 결과벡터들의 집합, 즉 span은 어떻게 될까?

쉽게 상상할 수 있는 것처럼(하나의 면이 면에 속하지 않은 방향으로 확장이 되면서) 모든 3차원 공간이 span이 될 것이다. 물론 아래와 같이 [!]예외는 존재한다.

💫 (3차원에서의) 선형 종속(Linear Dependent)

  • 세 개의 벡터 중 1개의 벡터가 나머지 2개의 벡터 span 내 존재할 경우
  • 세 개의 벡터 중 1개의 벡터가 나머지 2개의 벡터 선형 조합으로 표현 가능한 경우
    [+] 1개의 벡터를 추가 또는 제외하여도 span의 확장 또는 축소가 없는 경우 등




[+] Quiz :
The basis of a vector space is a set of linearly independent vectors that span the full space
벡터 공간의 기저는 전체 공간에 걸쳐 있는 선형 독립 벡터들의 집합입니다.


[+] R2\mathbb{R}^2, 2차원 벡터공간에서 두 개의 벡터가 서로 선형 독립(1개의 벡터를 다른 1개의 벡터의 선형결합으로 표현할 수 없는)일 경우에 꼭 직교할 필요가 없다. v⃗\vec{v} 또는 w⃗\vec{w}를 각각 w⃗\vec{w}, v⃗\vec{v}의 선형결합으로 표현할 수 없다. (y축 값에 대해서 서로 나타낼 수 없음)

v⃗=[10]\vec{v} = \begin{bmatrix} 1 \\ 0 \end{bmatrix}
w⃗=[11]\vec{w}= \begin{bmatrix} 1 \\ 1 \end{bmatrix}

[+] R2\mathbb{R}^2, 2차원 벡터공간에서 두 개의 벡터가 서로 선형 종속(1개의 벡터를 다른 1개의 벡터의 선형결합으로 표현할 수 있는)일 경우에는 상수배, 즉 Scalar Multiplication으로의 표현이 가능한 경우이다, 즉 선에 종속된다. (벡터합을 해줄 다른 벡터가 없잖아)

v⃗=c⋅w⃗\vec{v} = c \cdot \vec{w}

[+] R3\mathbb{R}^3, 3차원 벡터공간에서 1개의 벡터가 다른 벡터(들)에 선형 종속(1개의 벡터를 다른 2개의 벡터의 선형결합으로 표현할 수 있는)일 경우에는 면에 종속된다. 앞서 언급한 내용처럼 면에 선형 종속된 벡터는 꼭 그 면에 orthogonal할 필요는 없다.

v⃗=c1⋅w⃗+c2⋅u⃗\vec{v} = c_1 \cdot \vec{w} + c_2 \cdot \vec{u}
profile
olxtar
예술과 기술
이전 포스트

Vectors | Chapter 1, Essence of Linear Algebra [3Blue1Brown]

다음 포스트

선형 변환 및 행렬 | Chapter 3, Essence of Linear Algebra [3Blue1Brown]

0개의 댓글