Comment :
추천시스템 어쩌구,,, 특이값 분해(Singular Value Decomposition, SVD) 저쩌구를 이해하려다가 여기까지 옴. (SVD까지 필요한 개념들이) 제일 깔끔하게 잘 정리된 공돌이의 수학정리노트를 학습함.Reference 행렬 곱에 대한 또다른 시각 - 공돌이의 수학정리노트(Angelo's Math Notes)
[+] 행렬 TeX 문법 : $\begin{bmatrix} 0 & 1 \\ 2 & 3 \end{bmatrix}$ → \rightarrow → [ 0 1 2 3 ] \begin{bmatrix} 0 & 1 \\ 2 & 3 \end{bmatrix} [ 0 2 1 3 ]
일반적인 행렬곱
행렬(간의) 곱에 대해서는 그냥 외웠다는것이 기억난다. 앞쪽에 있는 행렬의 행과 뒷쪽에 있는 행렬의 열을 내적하여 각 인덱스에 맞게 넣어둔 행렬이 행렬곱의 결과물이다. 정도로 알고 있었다.
즉 수식으로 표현하면 다음과 같다.
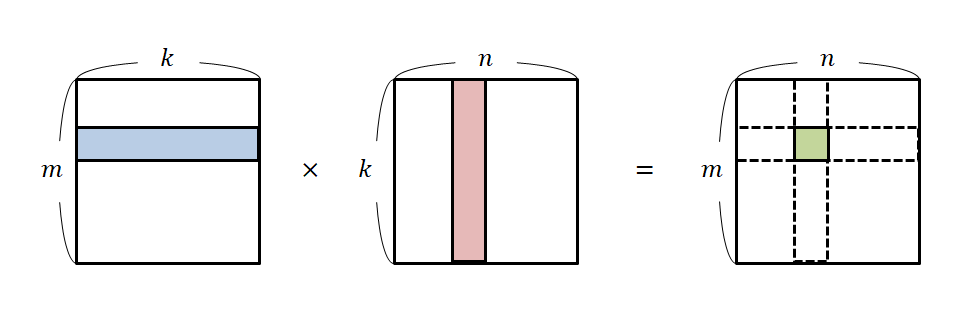
[ 1 2 3 4 ] [ a b c d ] = [ 1 ⋅ a + 2 ⋅ c 1 ⋅ b + 2 ⋅ d 3 ⋅ a + 4 ⋅ c 3 ⋅ b + 4 ⋅ d ] \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} a & b \\ c & d \end{bmatrix} = \begin{bmatrix} 1 \cdot a + 2 \cdot c & 1 \cdot b + 2 \cdot d \\ 3 \cdot a + 4 \cdot c & 3 \cdot b + 4 \cdot d \end{bmatrix} [ 1 3 2 4 ] [ a c b d ] = [ 1 ⋅ a + 2 ⋅ c 3 ⋅ a + 4 ⋅ c 1 ⋅ b + 2 ⋅ d 3 ⋅ b + 4 ⋅ d ] 🔰 즉, 좌측 행렬의 차원의 인덱스를 m , k m, k m , k k , n k, n k , n m m m n n n → \rightarrow → m m m n n n 위 수식처럼 2x2행렬 두개의 행렬곱의 경우,행렬곱 결과인 행렬의 1행1열 값은 = 좌측행렬 1행과 우측행렬 1열의 내적값행렬곱 결과인 행렬의 1행2열 값은 = 좌측행렬 1행과 우측행렬 2열의 내적값행렬곱 결과인 행렬의 2행1열 값은 = 좌측행렬 2행과 우측행렬 1열의 내적값행렬곱 결과인 행렬의 2행2열 값은 = 좌측행렬 2행과 우측행렬 2열의 내적값뭐 어찌보면, 행렬곱을 할때 좌측행렬의 열 차원과 우측행렬의 행 차원이 동일해야 이처럼 곱이 가능한 부분이기도 하다
열벡터의 선형 결합
다른 관점에서의 행렬곱을 이해하는 방법은 열벡터의 선형결합
이번에는 행렬간 곱이아닌(..?) 행렬과 벡터의 곱을 생각해보자
[ 1 2 3 4 ] [ a c ] = [ 1 ⋅ a + 2 ⋅ c 3 ⋅ a + 4 ⋅ c ] \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} a \\ c \end{bmatrix} = \begin{bmatrix} 1 \cdot a + 2 \cdot c \\ 3 \cdot a + 4 \cdot c \end{bmatrix} [ 1 3 2 4 ] [ a c ] = [ 1 ⋅ a + 2 ⋅ c 3 ⋅ a + 4 ⋅ c ] 이를 조금 다르게 보면 다음과 같다. (두 열벡터의 선형결합)
[ 1 2 3 4 ] [ a c ] = a ⋅ [ 1 3 ] + c ⋅ [ 2 4 ] \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} a \\ c \end{bmatrix} = a \cdot \begin{bmatrix} 1 \\ 3 \end{bmatrix} + c \cdot \begin{bmatrix} 2 \\ 4 \end{bmatrix} [ 1 3 2 4 ] [ a c ] = a ⋅ [ 1 3 ] + c ⋅ [ 2 4 ] a, c라는 상수값과 열벡터 (1,3), (2,4)간의 곱은 벡터의 상수배그리고 그 두개의 합이 바로 벡터의 합
다시 말해 행렬과 벡터의 곱은 행렬을 구성하고 있는 두 열벡터의 선형결합
1) 열공간을 기반한 해석
✅ 벡터의 선형결합 = 벡터 공간의 생성→ \rightarrow → 벡터의 기본 연산(상수배, 덧셈)
벡터 간 선형결합(Linear Combination) 중 상수배 합 (한꺼번에) 보자.
c 1 [ 1 0 ] + c 2 [ 0 1 ] c_1 \begin{bmatrix} 1 \\ 0 \end{bmatrix} + c_2 \begin{bmatrix} 0 \\ 1 \end{bmatrix} c 1 [ 1 0 ] + c 2 [ 0 1 ] 위 수식은 아래와 같이 해석할 수 있다. → \rightarrow → [ 1 0 ] \begin{bmatrix} 1 \\ 0 \end{bmatrix} [ 1 0 ] [ 0 1 ] \begin{bmatrix} 0 \\ 1 \end{bmatrix} [ 0 1 ] 벡터 공간
자 그러면 (행렬과 벡터간의 곱을 두 열벡터의 선형결합으로 보는 관점에 이어서...) 벡터공간, 즉 열공간(Column Space)
A x ⃗ = b ⃗ A \vec{x} = \vec{b} A x = b [ 1 2 3 4 ] [ x y ] = [ 3 5 ] \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 3 \\ 5 \end{bmatrix} [ 1 3 2 4 ] [ x y ] = [ 3 5 ] x [ 1 3 ] + y [ 2 4 ] = [ 3 5 ] x \begin{bmatrix} 1 \\ 3 \end{bmatrix} + y \begin{bmatrix} 2 \\ 4 \end{bmatrix} = \begin{bmatrix} 3 \\ 5 \end{bmatrix} x [ 1 3 ] + y [ 2 4 ] = [ 3 5 ] 이는
"[ 1 3 ] \begin{bmatrix} 1 \\ 3 \end{bmatrix} [ 1 3 ] (열) 벡터와 [ 2 4 ] \begin{bmatrix} 2 \\ 4 \end{bmatrix} [ 2 4 ] (열) 벡터로부터 생성된 벡터공간 [ 3 5 ] \begin{bmatrix} 3 \\ 5 \end{bmatrix} [ 3 5 ]
만약 존재한다면, [ 1 3 ] \begin{bmatrix} 1 \\ 3 \end{bmatrix} [ 1 3 ] (열) 벡터와 [ 2 4 ] \begin{bmatrix} 2 \\ 4 \end{bmatrix} [ 2 4 ] (열) 벡터를 x , y x, y x , y [ 3 5 ] \begin{bmatrix} 3 \\ 5 \end{bmatrix} [ 3 5 ]
라는 관점으로 해석할 수 있다.
2) 선형 변환을 기반한 해석
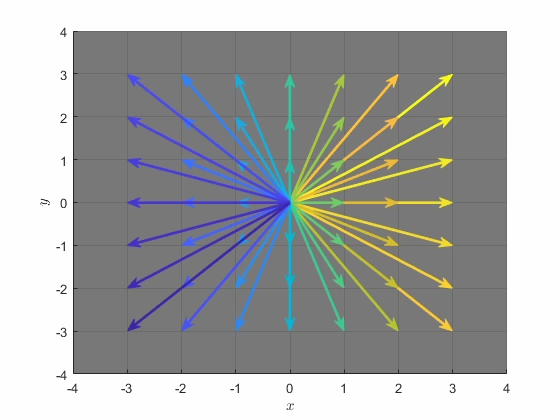
위처럼 행렬과 벡터의 곱이 열벡터의 선형결합 기저 벡터의 변형을 통한 벡터의 선형 변환
먼저 아래와 같은 행렬 A A A
A = [ 2 − 3 1 1 ] A = \begin{bmatrix} 2 & -3 \\ 1 & 1 \end{bmatrix} A = [ 2 1 − 3 1 ] (행렬 A A A 벡터 x ⃗ \vec{x} x
x ⃗ = [ 1 1 ] \vec{x} = \begin{bmatrix} 1 \\ 1 \end{bmatrix} x = [ 1 1 ] 변환시키면
A x ⃗ = [ 2 − 3 1 1 ] [ 1 1 ] A \vec{x} = \begin{bmatrix} 2 & -3 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \end{bmatrix} A x = [ 2 1 − 3 1 ] [ 1 1 ] A x ⃗ = [ 2 ⋅ 1 + ( − 3 ) ⋅ 1 1 ⋅ 1 + 1 ⋅ 1 ] A \vec{x} = \begin{bmatrix} 2 \cdot 1 + (-3) \cdot 1 \\ 1 \cdot 1 + 1 \cdot 1 \end{bmatrix} A x = [ 2 ⋅ 1 + ( − 3 ) ⋅ 1 1 ⋅ 1 + 1 ⋅ 1 ] = [ − 1 2 ] = \begin{bmatrix} -1 \\ 2 \end{bmatrix} = [ − 1 2 ]
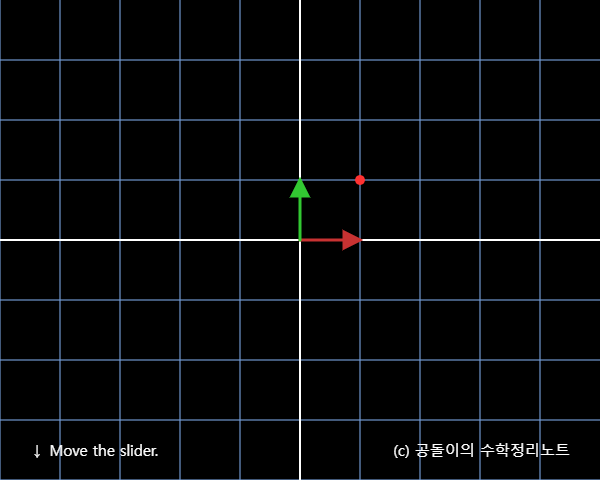
자 원래있었던 변환 이전 벡터 x ⃗ = [ 1 1 ] \vec{x} = \begin{bmatrix} 1 \\ 1 \end{bmatrix} x = [ 1 1 ]
이 벡터 x ⃗ \vec{x} x A = [ 2 − 3 1 1 ] A = \begin{bmatrix} 2 & -3 \\ 1 & 1 \end{bmatrix} A = [ 2 1 − 3 1 ] 선형 변환 (아직 선형변환이라는 말이 와닿지 않아도 된다. 아래 그림과 설명을 보며 느껴보자) 해주면 아래와 같이 된다.
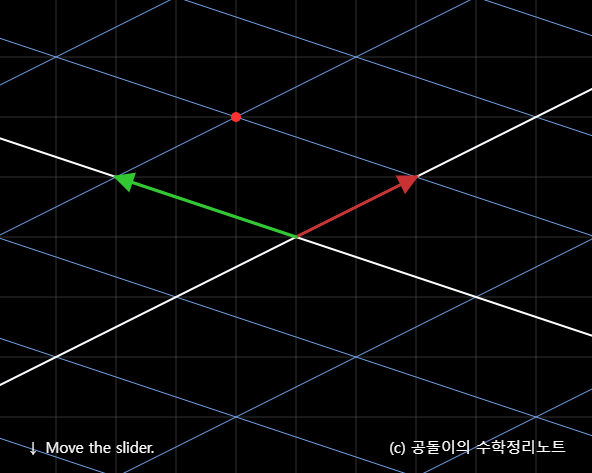
앞서 하였던 선형변환의 결과 벡터는 [ − 1 2 ] \begin{bmatrix} -1 \\ 2 \end{bmatrix} [ − 1 2 ] b ⃗ \vec{b} b (뒤에있는 회색 격자의) 일반적인? 벡터공간으로 보면 빨간색 점 인 벡터 b ⃗ \vec{b} b
자 이번에는 위 그림에서 (뒤에있는 회색 격자는 무시하고) 사선으로 그려져있는 파란색 격자 를 보자. 좀 뭉개져? 눕혀져? 있지만 빨간색 점 인 벡터는 파란색 격자기준, (1,1)이라는 지점에 있다.
뭔가 신기하면서도 와닿지가 않는데...
먼저 2x2, 즉 두개의 열벡터로 이루어져있는 행렬 A A A x ⃗ \vec{x} x (이 벡터의 기저벡터는 일반적인 x축 y축 단위벡터?)
A x ⃗ = b ⃗ A \vec{x} = \vec{b} A x = b 라고 하고 x ⃗ \vec{x} x i ^ , j ^ \hat{i}, \hat{j} i ^ , j ^
i ^ = [ 1 0 ] , j ^ = [ 0 1 ] \hat{i} = \begin{bmatrix} 1 \\ 0 \end{bmatrix}, \space \space \space \space \hat{j} = \begin{bmatrix} 0 \\ 1 \end{bmatrix} i ^ = [ 1 0 ] , j ^ = [ 0 1 ] 선형변환에 의하여 새롭게 변형된 기저벡터(=행렬A의 두 열벡터) 를 i n e w ^ , j n e w ^ \hat{i_{new}}, \hat{j_{new}} i n e w ^ , j n e w ^
i n e w ^ = [ A 0 , 0 A 1 , 0 ] , j n e w ^ = [ A 0 , 1 A 1 , 1 ] \hat{i_{new}} = \begin{bmatrix} A_{0,0} \\ A_{1,0} \end{bmatrix}, \space \space \space \space \hat{j_{new}} = \begin{bmatrix} A_{0,1} \\ A_{1,1} \end{bmatrix} i n e w ^ = [ A 0 , 0 A 1 , 0 ] , j n e w ^ = [ A 0 , 1 A 1 , 1 ] 선형변환의 결과물인, 즉 행렬과 벡터간의 곱의 결과물인 b ⃗ \vec{b} b i n e w ^ , j n e w ^ \hat{i_{new}}, \hat{j_{new}} i n e w ^ , j n e w ^ x ⃗ \vec{x} x (?)