1. Logistic Regression
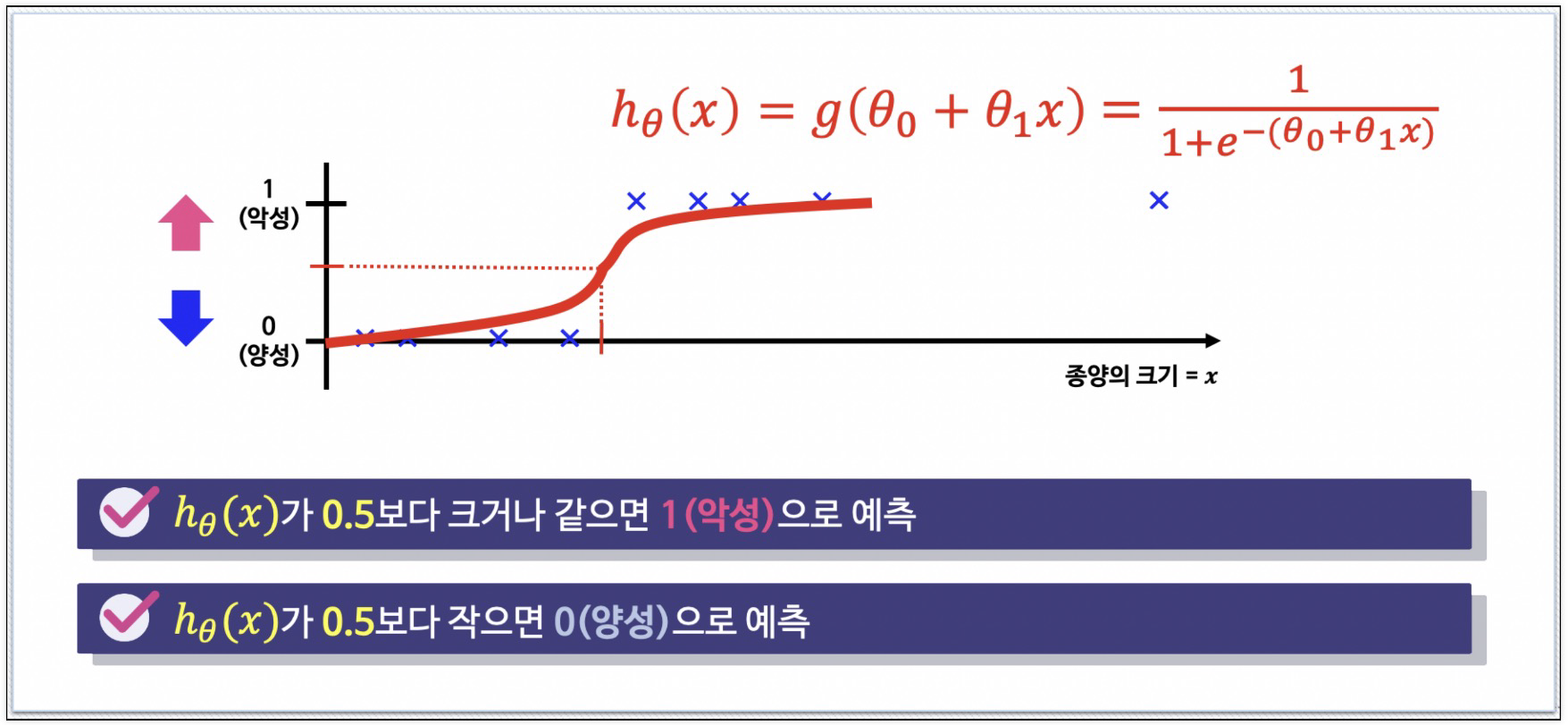
- 분류 문제는 0 또는 1로 예측해야 하나 Linear Regression을 그대로 적용하면 예측값 hθ(x)는 0보다 작거나 1보다 큰 값을 가질 수 있다.
- hθ(x)가 항상 0 ~ 1을 가지는 모델
g(z)=1+e−z1 
분류 문제용 hypothesis
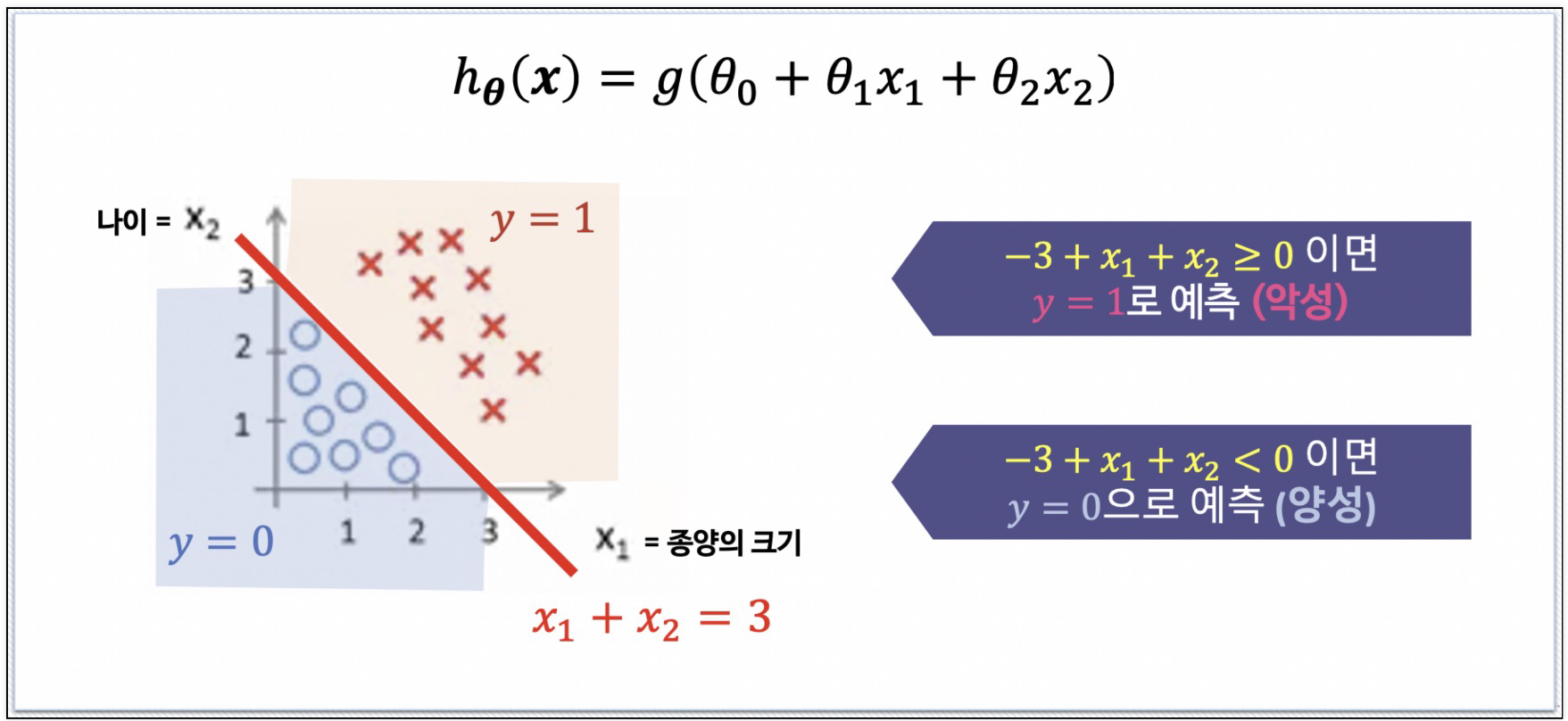
Decision Boundary1
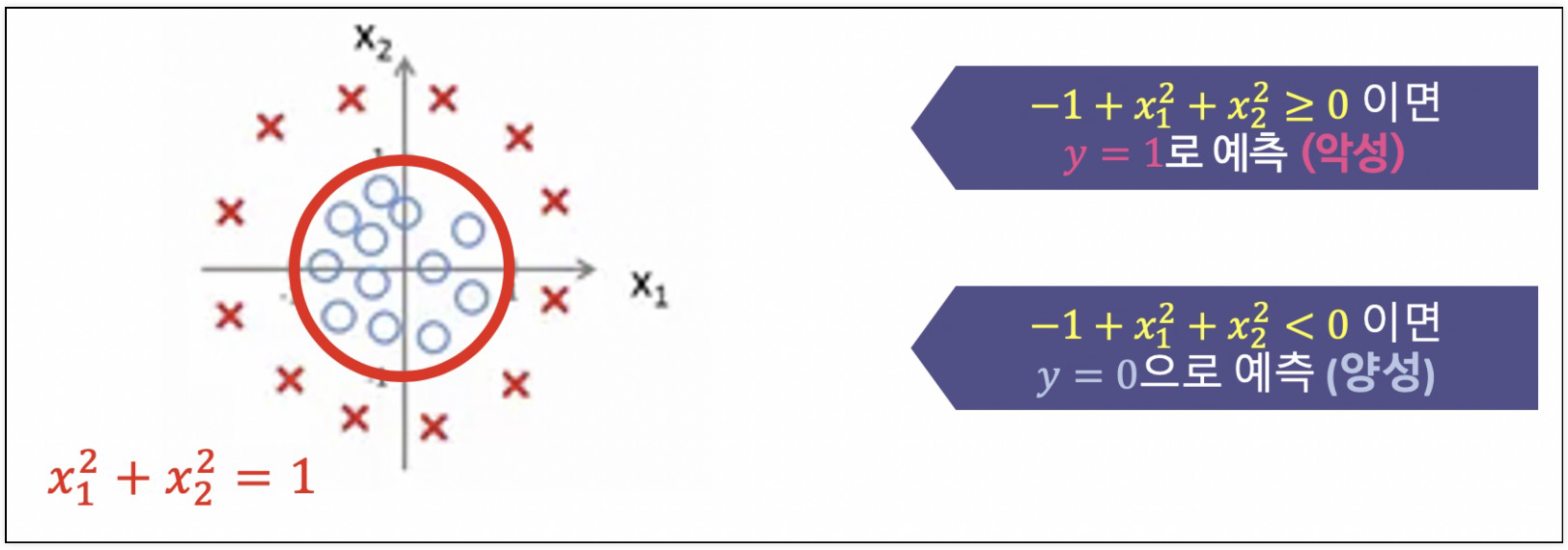
Decision Boundary2
Cost Function
J(θ)=m1i=1∑mCost(hθ(xi),yi)Cost(hθ(x),y)={−log(hθ(x))y=1−log(1−hθ(x))y=0}
Learning 알고리즘은 동일
- 수렴할 때까지 반복
- α : 학습률(learning rate)
θ:=θ−αdθdJ(θ)
Reference
1) 제로베이스 데이터스쿨 강의자료




