OLS

머신러닝

1) 지도학습

• 정답이 있는 데이터 학습
• 종류: 분류 Classification, 회귀 Regression

회귀 Regression

• 학습데이터셋 → 학습 알고리즘 → h(Hypothesis 가설 = 모델)
• 어떤 feature를 기준으로, 연속된 값을 예측하는 문제(주어진 데이터가 정답과 가장 잘 맞는 Hypothesis을 찾는 것)
• 선형 회귀: $h_θ(x) = θ_0 + θ_1x$

2) 비지도학습

• 정답 레이블이 없는 데이터 학습
• 종류: 군집, 차원 축소

OLS(Ordinary Linear Least Square, 최소자승법)

1) 최소자승법 OLS

• 잔차제곱합(RSS: Residual Sum of Squares)를 최소화하는 가중치 벡터를 구하는 방법
• 찾고자 하는 모델: $y = ax + b$
• 행렬과 벡터로 표현:
  $Y = AX, Y=\begin{pmatrix}y_1\\y_2\\..\\y_n \end{pmatrix}, \; A=\begin{pmatrix}x_1&1\\x_2&1\\..\\x_n&1 \end{pmatrix}, \; X=\begin{pmatrix}a\\b\\\end{pmatrix}$
  $A^TAX = A^TY\\ X = (A^TA)^{-1}A^TY$
• $A^T$ : transposed matrix(전치행렬, 행과 열을 바꾼 행렬)
• $(A^TA)$ : 본 행렬과 전치행렬의 곱은 정방행렬로 역행렬로 바꾸는 것이 가능해진다.
• 모델 성능은 에러로 표현: $\sum(예측-실제값)^2$ or $\sum|예측-실제값|$

!pip install statsmodels

# 데이터
import pandas as pd
data = {'x':[1, 2, 3, 4, 5], 'y':[1, 3, 4, 6, 5]}
df = pd.DataFrame(data)

# 가설
import statsmodels.formula.api as smf
lm_model = smf.ols(formula='y ~ x', data=df).fit()
lm_model.params # y절편, x 결과

# 시각화
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.lmplot(x='x', y='y', data=df);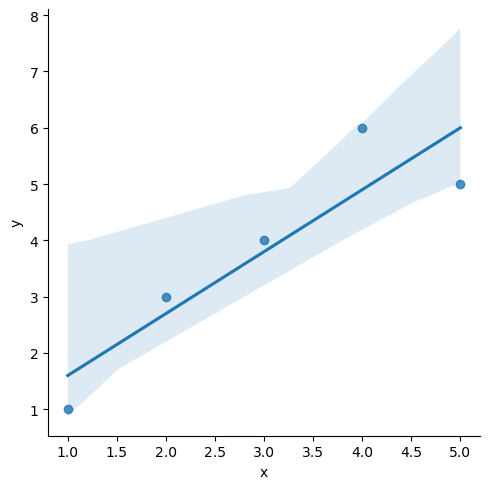

2) 잔차 평가 residue

• 잔차는 평균이 0인 정규분포를 따르는 것 이어야 함
• 잔차 평가는 잔차의 평균이 0이고 정규분포를 따르는 지 확인

resid = lm_model.resid # resid
reside
'''
0   -0.6
1    0.3
2    0.2
3    1.1
4   -1.0
dtype: float64
'''

3) 결정계수 R-Squared

• R-Squared = $\sum (예측값 - 평균)^2 / \sum (참값 - 평균)^2$
• 예측 값과 실제 값(y)이 일치하면 결정계수는 1이 됨 (결정계수가 높을 수록 좋은 모델)

#numpy로 직접 계산
import numpy as np
mu = np.mean(df.y) # 참값의 평균
y = df.y # 참값
yhat = lm_model.predict() # 예측값
np.sum((yhat - mu)**2) / np.sum((y - mu)**2) # 0.8175675675675671

lm_model.rsquared # 0.8175675675675671 간단하게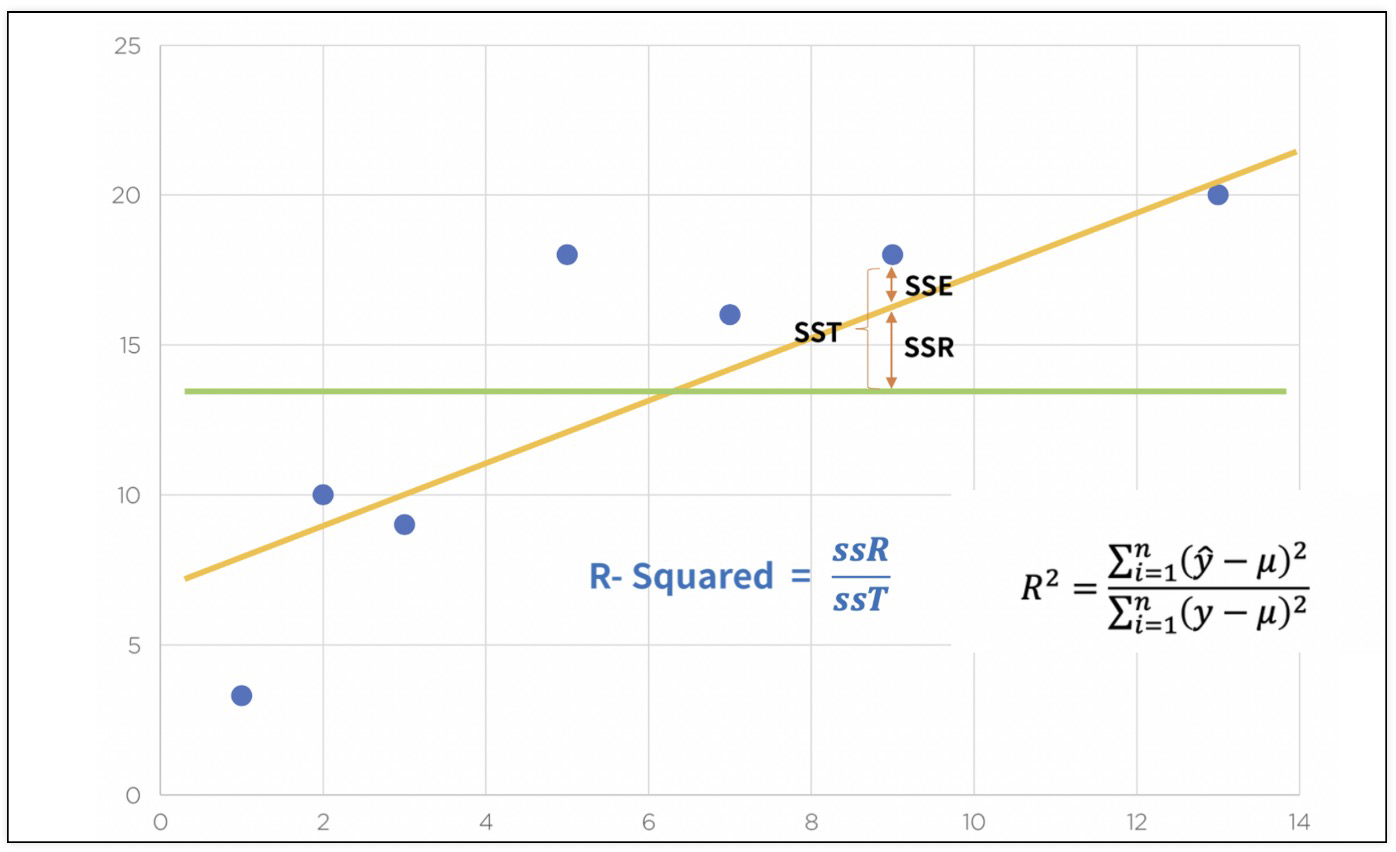

• summary(): 모델 리포트
  • 회귀 리포트 → R-Squared(결정계수, 모형 적합도), coef(계수), std err(계수에 대한 편차), P>|t|(p-value)
  • formula는 원래 자동으로 상수항 만들어짐, 데이터 컬럼으로 넣으면 상수항을 만들어줘야 한다.
  • Adj. R-squared : 독립변수가 여러 개인 다중회귀분석에서 사용
  • Prob. F-Statistic : 회귀모형에 대한 통계적 유의미성 검정. 이 값이 0.05 이하라면 모집단에서도 의미가 있다고 볼 수 있음

---

Reference
1) 제로베이스 데이터스쿨 강의자료
2) 선형회귀분석의 기초