1. 모델 평가
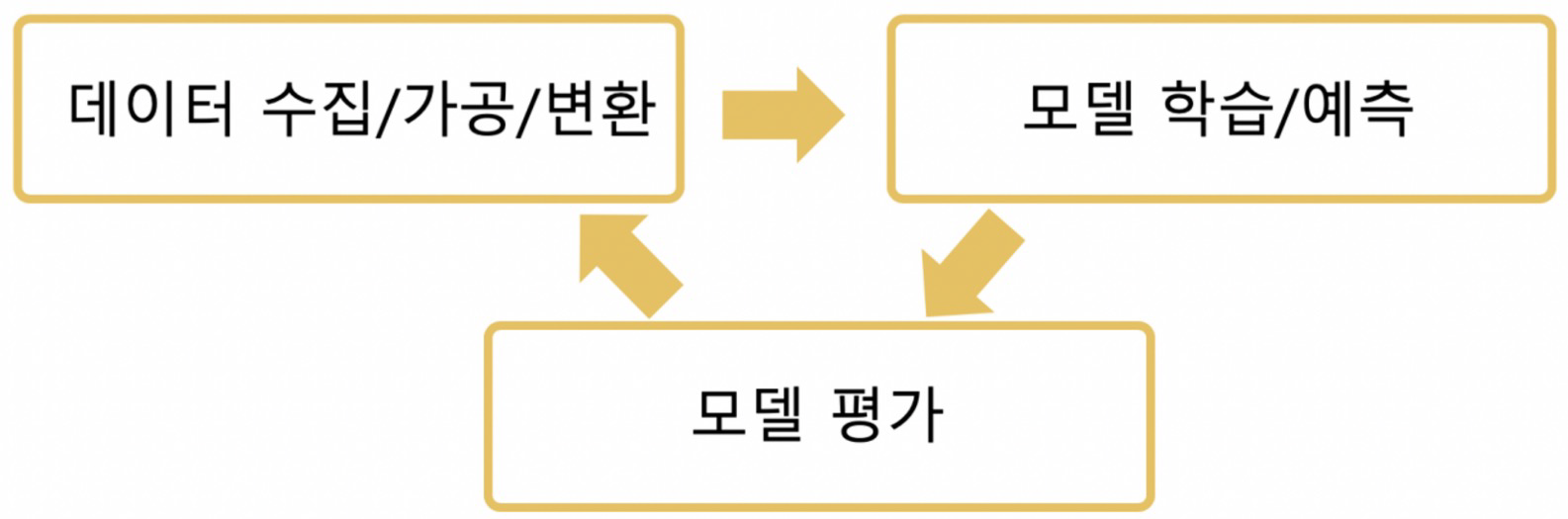
회귀모델(연속된 값 예측) 모델평가
- 실제 값과의 에러치를 가지고 계산
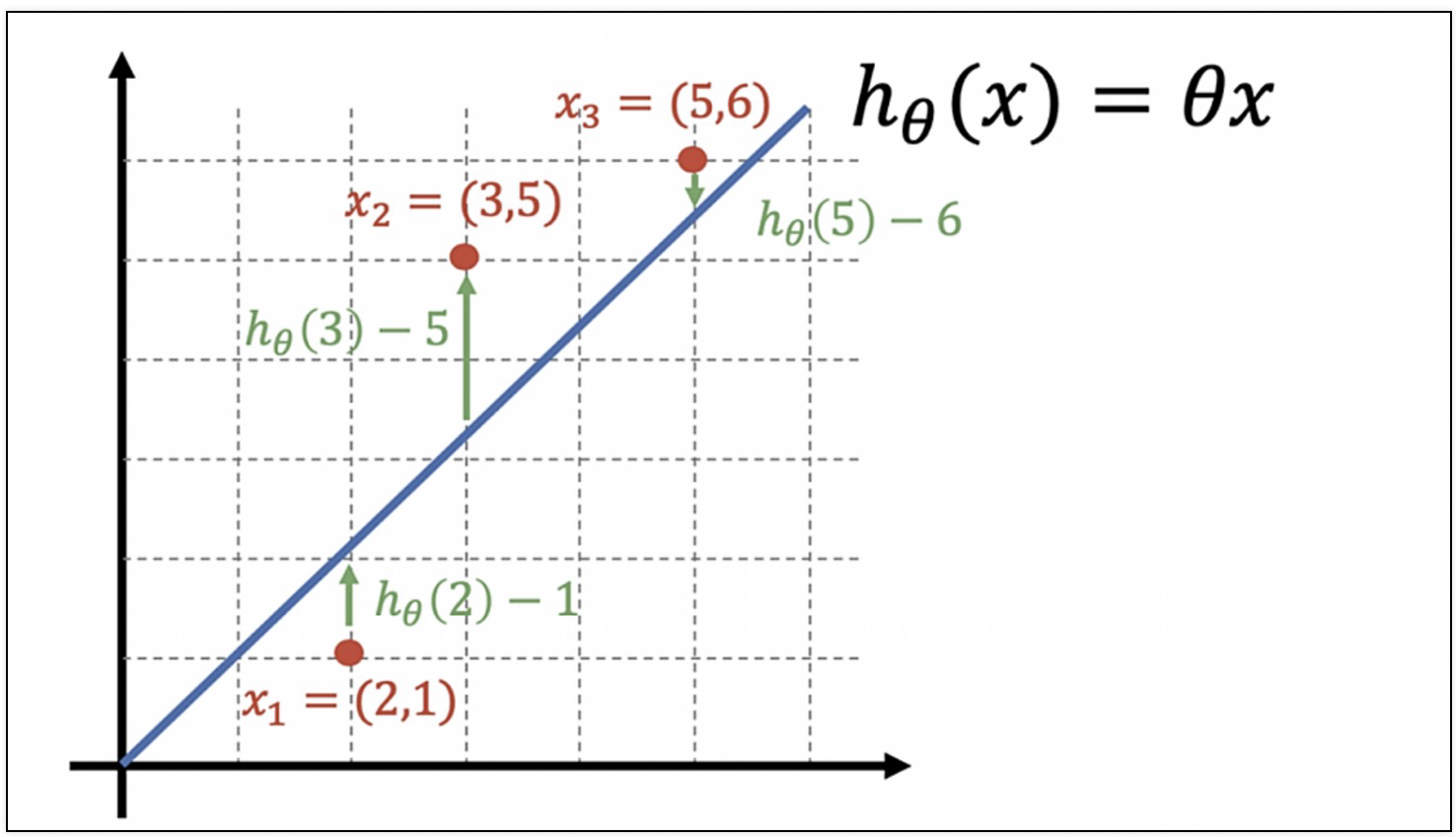
분류 모델
- 평가 항목은 많다.
- 분류모델은 그 결과를 속할 비율(확률)을 반환한다.

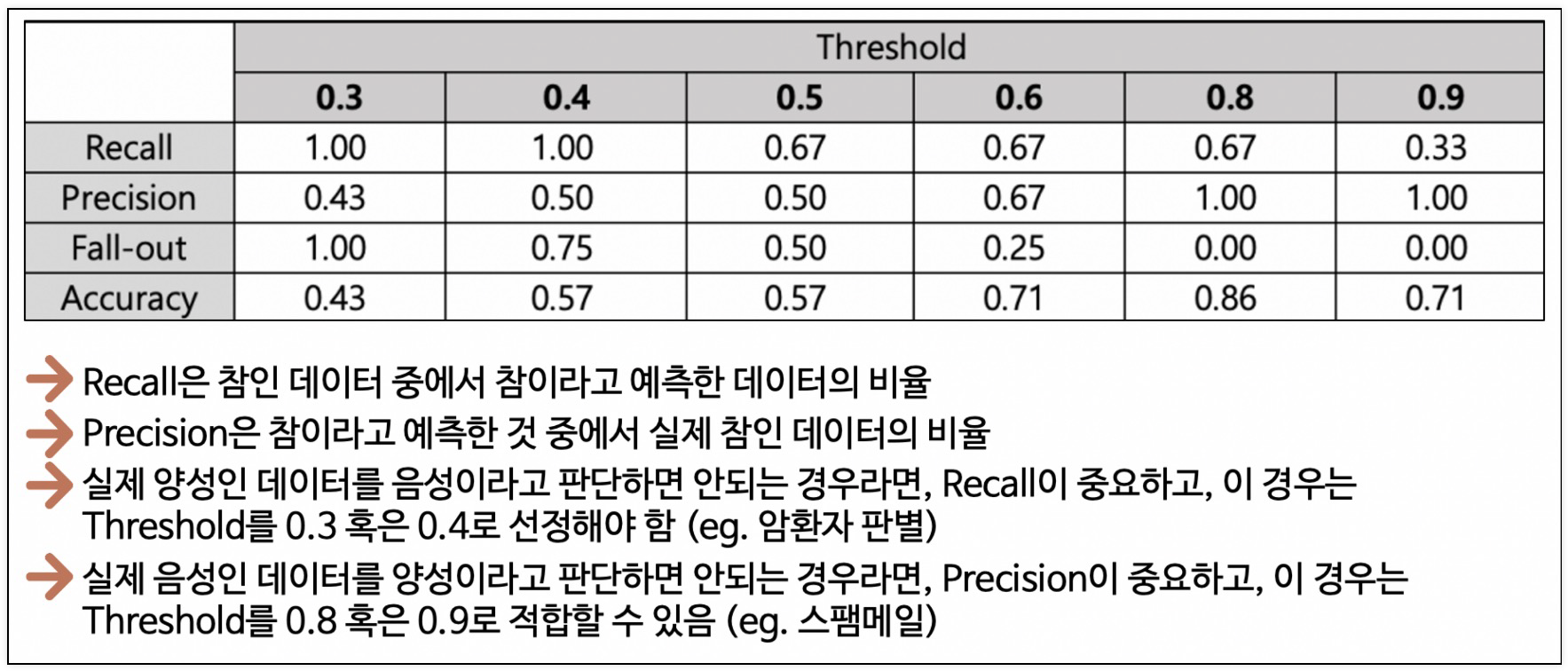
이진 분류 모델의 평가
- 비율에서 threshold를 0.5라고 하고 0, 1로 결과를 반영했다.
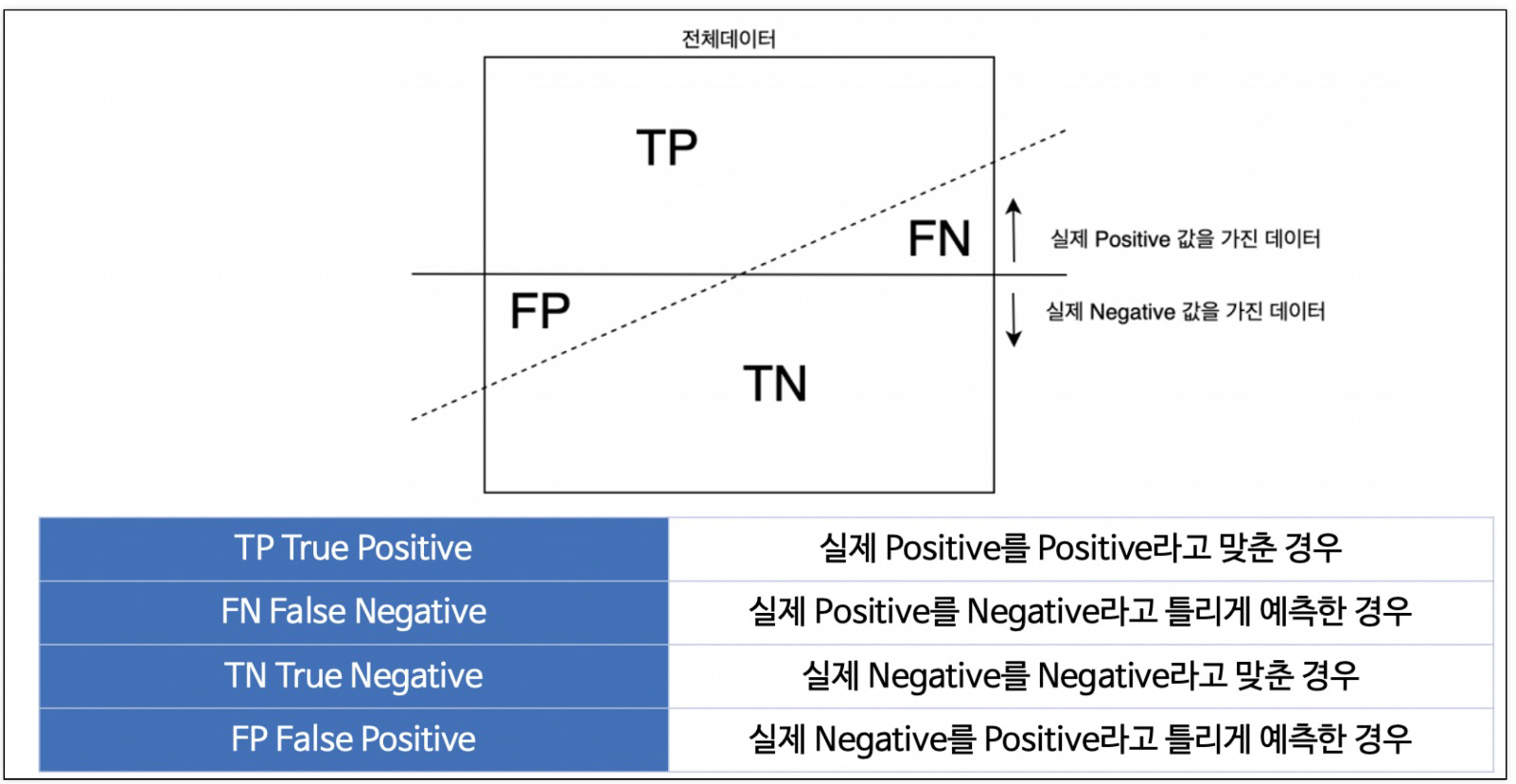
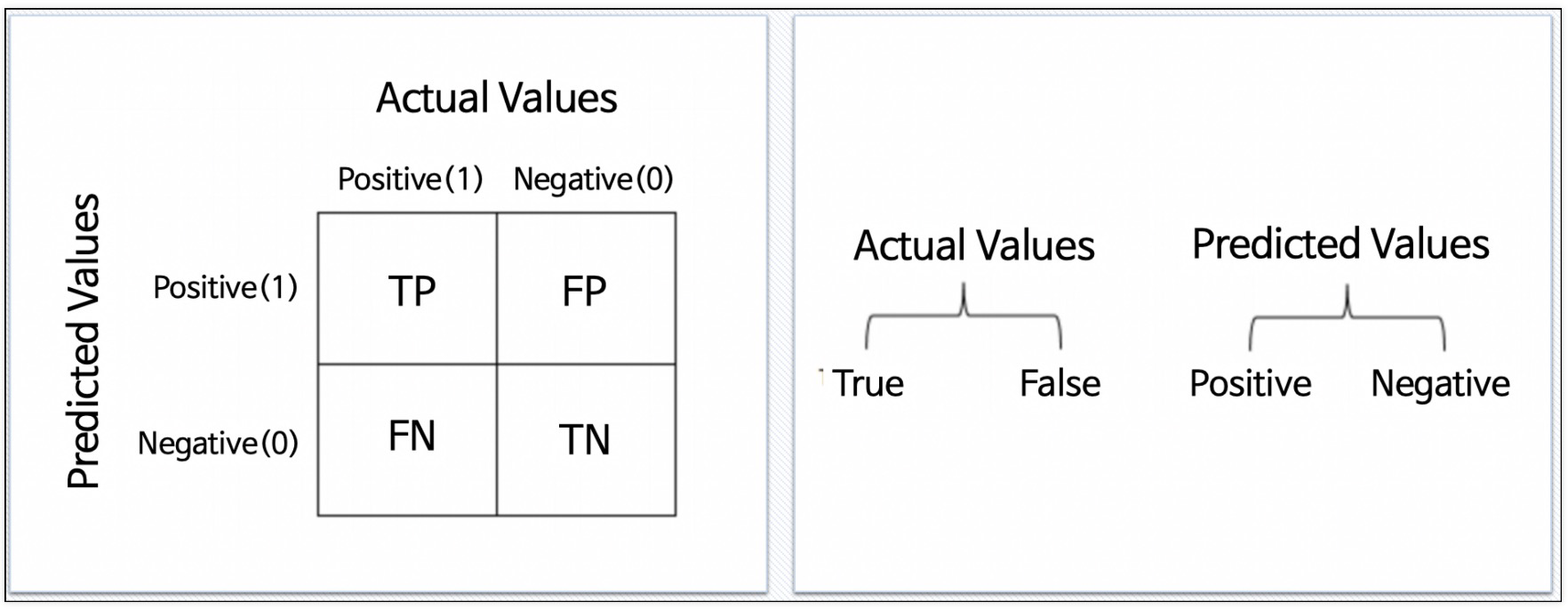
Accuracy
- 전체 데이터 중 맞게 예측한 비율
Precision
- 양성이라고 예측한 것 중에서 실제 양성 비율
RECALL (TPR TRUE POSITIVE RATIO)
- 참인 데이터들 중에서 참이라고 예측한 것
FALL-OUT (FPR FALSE POSITION RATIO)
- 실제로 양성이 아닌데, 양성이라고 잘못 예측한 경우
F1-score
- F1-score는 precision과 recall을 결합한 지표
- precision과 recall이 모두 치우치지 않고 높은 값을 가질수록 높은 값을 가진다.
정리
- Recall과 Precision은 서로 영향을 주기 때문에 한 쪽을 극단적으로 높게 설정해서는 안된다.
- 여기서부터는 추가 내용
함수
자연상수 e
- 2.718281828459045에 수렴
로그함수
def log(x, base):
return np.log(x)/np.log(base)시그모이드 Sigmoid
z = np.linspace(-10, 10, 100)
sigma = 1/(1+np.exp(-z))
plt.figure(figsize=(12,8))
plt.plot(z, sigma)
plt.xlabel('$z$', fontsize=25)
plt.ylabel('$\sigma(z)$', fontsize=25)
plt.show()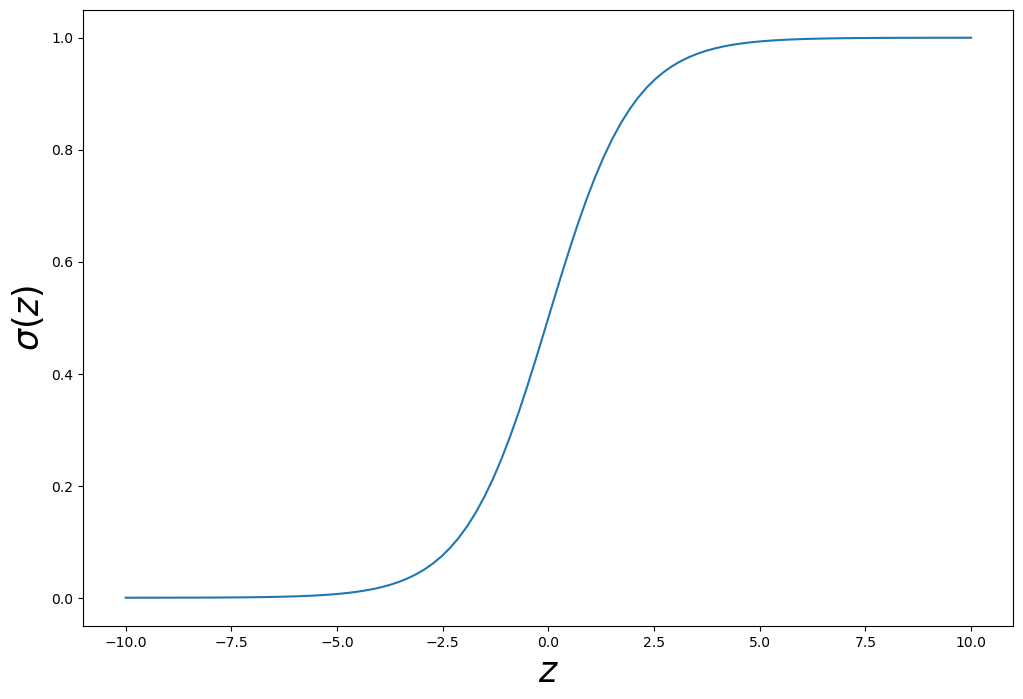
함수의 표현
벡터의 표현
단일 변수 스칼라 함수
다중 변수 스칼라 함수
다변수 벡터 함수
예제
u = np.linspace(0, 1, 30)
v = np.linspace(0, 1, 30)
X, Y = np.meshgrid(u, v)
Z = (1 + X**2) + (Y/(1+Y**2))
fig = plt.figure(figsize=(7, 7))
ax = plt.axes(projection='3d')
ax.xaxis.set_tick_params(labelsize=15)
ax.yaxis.set_tick_params(labelsize=15)
ax.zaxis.set_tick_params(labelsize=15)
ax.set_xlabel(r'$x$', fontsize=20)
ax.set_ylabel(r'$y$', fontsize=20)
ax.set_zlabel(r'$z$', fontsize=20)
ax.scatter3D(X, Y, Z, marker='.', color='gray')
plt.show()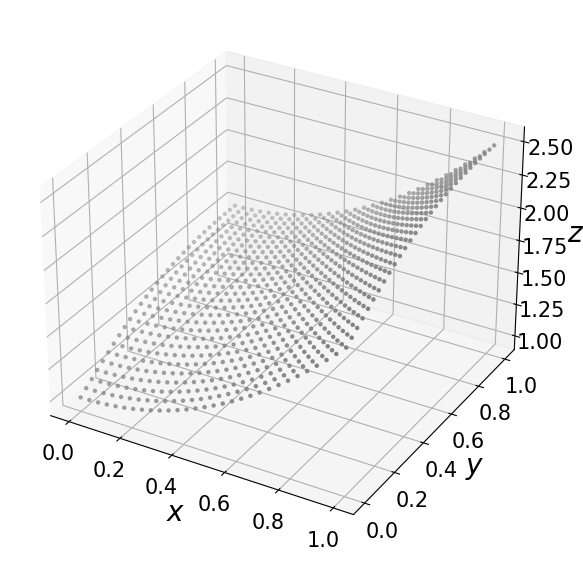
Boxplot
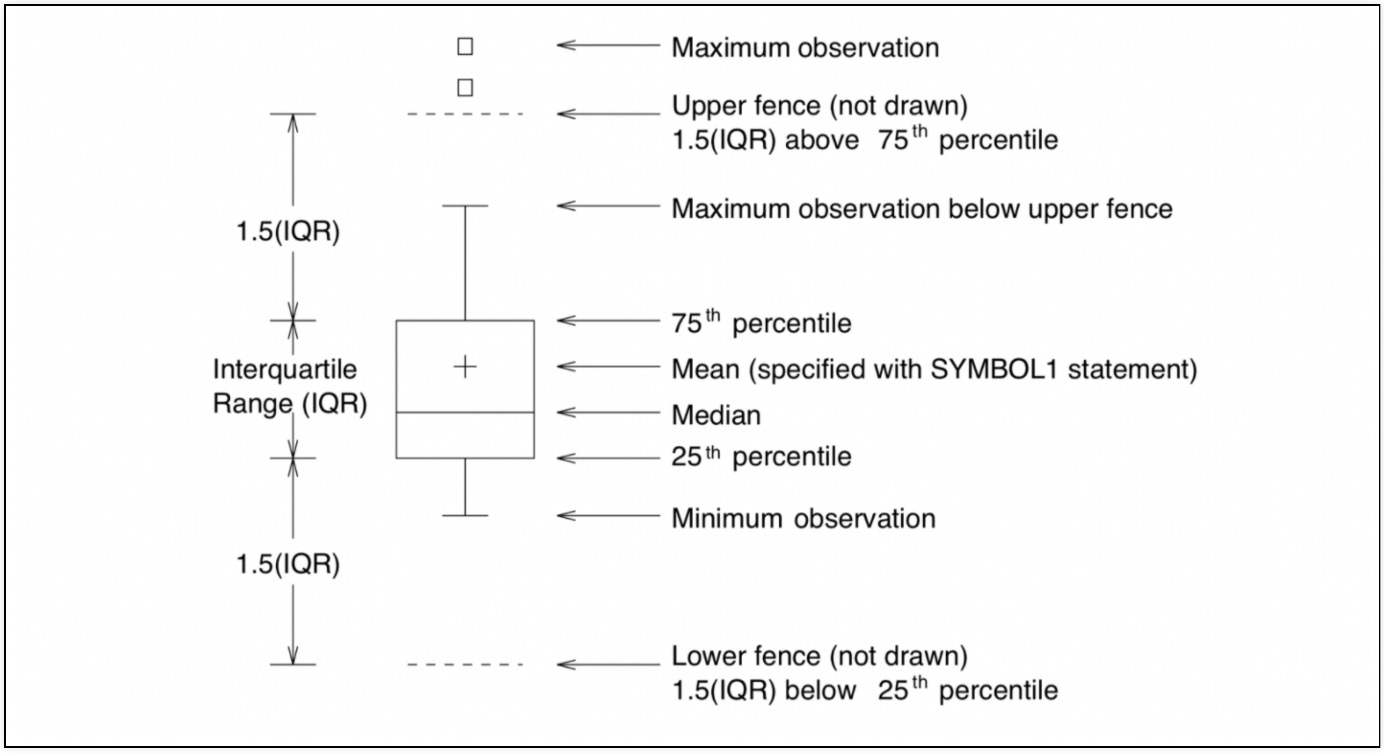
seaborn Boxplot의 원리
sample = [1, 7, 9, 16, 36, 39, 45, 45, 46, 48, 51, 100, 101]
tmp_y = [1]*len(sample)
q1 = np.percentile(sample, 25)
q2 = np.percentile(sample, 50)
q3 = np.percentile(sample, 75)
iqr = np.percentile(sample, 75) - np.percentile(sample, 25)
upper_fence = q3 + iqr*1.5
lower_fence = q1 - iqr*1.5
plt.figure(figsize=(12, 4))
plt.scatter(sample, tmp_y)
plt.axvline(x=q1, color='black')
plt.axvline(x=q2, color='red')
plt.axvline(x=q3, color='black')
plt.axvline(x=upper_fence, color='black', ls='dashed')
plt.axvline(x=lower_fence, color='black', ls='dashed')
plt.grid()
plt.show()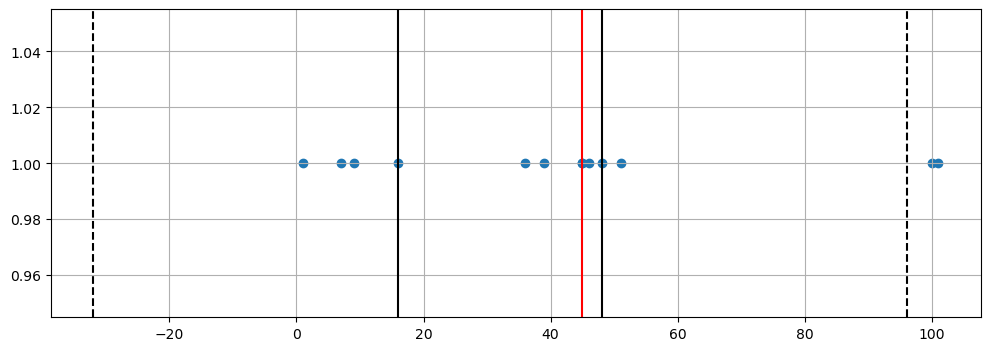
Reference
1) 제로베이스 데이터스쿨 강의자료
