오토인코더
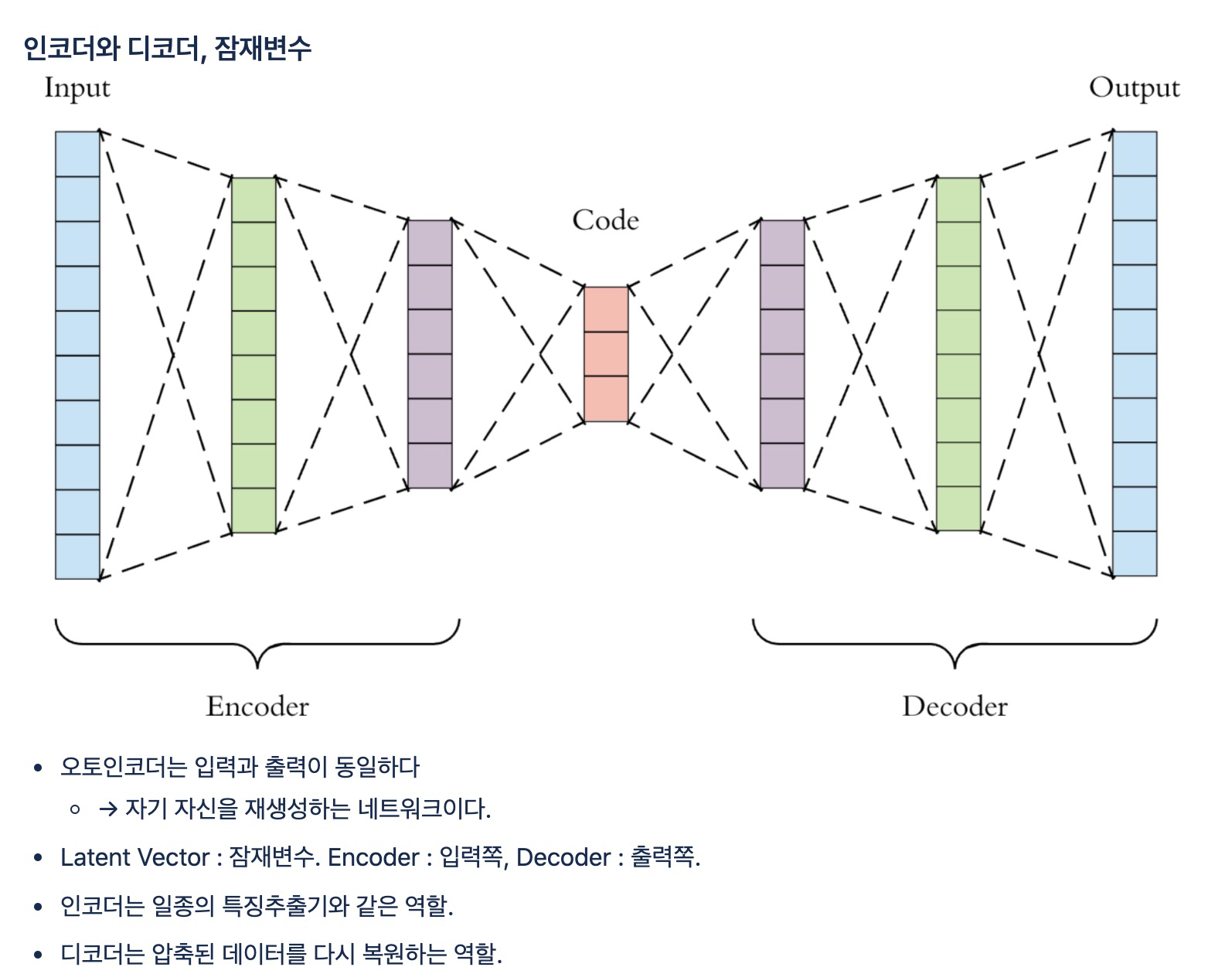
MNIST 데이터 실습
1. 데이터 불러오기
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
(train_X, train_Y), (test_X, test_Y) = tf.keras.datasets.mnist.load_data()
print(train_X.shape, train_Y.shape) #(60000, 28, 28) (60000,)
# 정규화
train_X = train_X / 255.0
test_X = test_X / 255.02. 모양확인
# 모양 확인
plt.imshow(train_X[0].reshape(28, 28), cmap='gray')
plt.colorbar()
plt.show()
print(train_Y[0])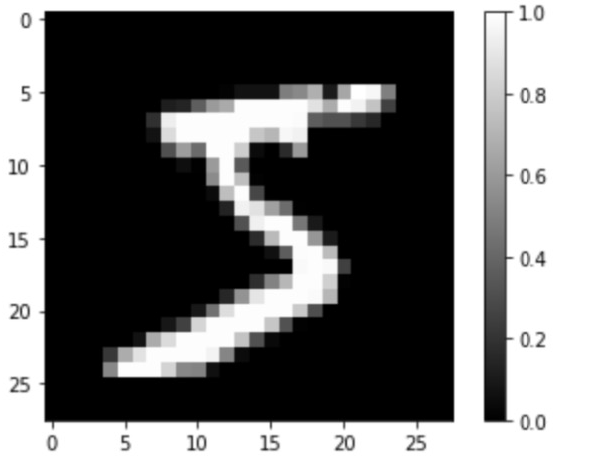
3. 모델 정의
train_X = train_X.reshape(-1, 28 * 28)
test_X = test_X.reshape(-1, 28 * 28)
print(train_X.shape, train_Y.shape) #Flatten대신, 입력과 출력의 형태가 같아야 하기 때문
# Dense 오토인코더 모델 정의
model = tf.keras.Sequential([
tf.keras.layers.Dense(784, activation='relu', input_shape=(784,)),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.Dense(784, activation='sigmoid')
])
model.compile(optimizer=tf.optimizers.Adam(), loss='mse')
model.summary()
# dense와 dense_2의 레이어는 뉴런의 수가 같아서 대칭을 이루며, 각각 인코더와 디코더의 역할
# desne_1는 잠재변수로 뉴런의 수가 적은 것을 확인4. 모형 시각화
# Dense 오토 인코더 모델 학습
model.fit(train_X, train_X, epochs=10, batch_size=256)
import random
plt.figure(figsize=(4,8))
for c in range(4):
plt.subplot(4, 2, c*2+1)
rand_index = random.randint(0, test_X.shape[0])
plt.imshow(test_X[rand_index].reshape(28, 28), cmap='gray')
plt.axis('off')
plt.subplot(4, 2, c*2+2)
img = model.predict(np.expand_dims(test_X[rand_index], axis=0))
plt.imshow(img.reshape(28, 28), cmap='gray')
plt.axis('off')
plt.show()
model.evaluate(test_X, test_X) # 0.0061719720251858234
5. CNN활용
# CNN 활용
# 흑백 이미지이기 때문에 마지막 차원의 수는 1
train_X = train_X.reshape(-1, 28, 28, 1)
test_X = test_X.reshape(-1, 28, 28, 1)
model = tf.keras.Sequential([
# Conv2D layer 2개, kernel_size=2, strides=(2,2)로 설정해 풀링 레이어 효과 -> 7x7
tf.keras.layers.Conv2D(filters=32, kernel_size=2, strides=(2,2), activation='relu', input_shape=(28, 28, 1)),
tf.keras.layers.Conv2D(filters=64, kernel_size=2, strides=(2,2), activation='relu'),
# 3차원에서 1차원
tf.keras.layers.Flatten(),
# 잠재 변수를 만들기 위해 Dense 오토인코더와 동일한 크기로 64개의 뉴런을 가지는 Dense레이어를 배치
tf.keras.layers.Dense(64, activation='relu'),
# 디코더는 인코더와 대칭이 되도록 다시 쌓는다. 잠재변수 레이어와 연결된 레이어는 7X7 이미지를 만들기 위해 64개의 채널만큼 가지고 있는 Conv2D레이어
tf.keras.layers.Dense(7*7*64, activation='relu'),
# 차원인 데이터를 3차원으로 바꿔주기 위해 64개의 채널만큼 Reshape레이어
tf.keras.layers.Reshape(target_shape=(7,7,64)),
# 대칭 구조를 만들기
tf.keras.layers.Conv2DTranspose(filters=32, kernel_size=2, strides=(2,2), padding='same', activation='relu'),
tf.keras.layers.Conv2DTranspose(filters=1, kernel_size=2, strides=(2,2), padding='same', activation='sigmoid')
])
model.compile(optimizer=tf.optimizers.Adam(), loss='mse')
model.summary()6. 모형 시각화
model.fit(train_X, train_X, epochs=10, batch_size=256)
# 결과 오토인코더의 이미지 재생성 및 모형 성능 평가
import random
plt.figure(figsize=(4,8))
for c in range(4):
plt.subplot(4, 2, c*2+1)
rand_index = random.randint(0, test_X.shape[0])
plt.imshow(test_X[rand_index].reshape(28, 28), cmap='gray')
plt.axis('off')
plt.subplot(4, 2, c*2+2)
img = model.predict(np.expand_dims(test_X[rand_index], axis=0))
plt.imshow(img.reshape(28, 28), cmap='gray')
plt.axis('off')
plt.show()
model.evaluate(test_X, test_X) # loss 0.0208229385316371927. elu
- 활성화함수(=activation) 문제
relu: 양수는 그대로 반환하고 0이나 음수가 들어오면 0을 반환- 뉴런의 계산값 중 음수가 되는 결과가 많을 경우 뉴런의 출력은 무조건 0이 된다. 출력은 다음 레이어의 가중치에 곱해지기 때문에 출력이 0이면 가중치의 효과를 모두 0으로 만든다. →
elu개념이 도입 : -1로 수렴
import math
x = np.arange(-5, 5, 0.01)
relu = [0 if z<0 else z for z in x]
elu = [1.0 * (np.exp(z) - 1) if z < 0 else z for z in x]
plt.axvline(0, color='gray')
plt.plot(x, relu, 'r--', label='relu')
plt.plot(x, elu, 'g--', label='elu')
plt.legend()
plt.show()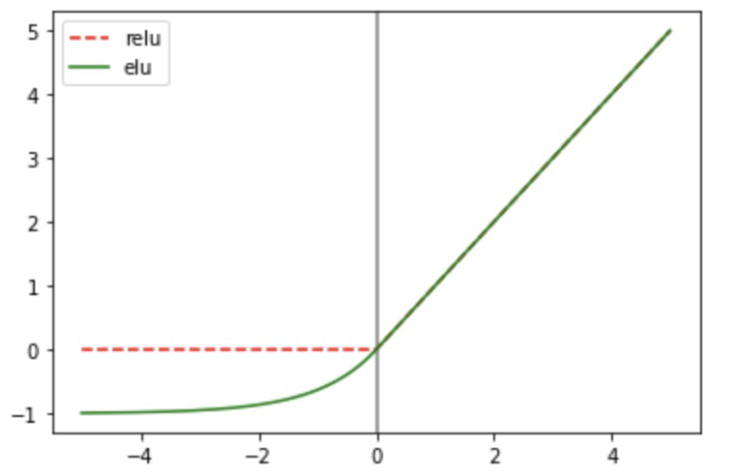
8. 모델 다시 정의
# elu로 수정
train_X = train_X.reshape(-1, 28, 28, 1)
test_X = test_X.reshape(-1, 28, 28, 1)
model = tf.keras.Sequential([
tf.keras.layers.Conv2D(filters=32, kernel_size=2, strides=(2,2), activation='elu', input_shape=(28, 28, 1)),
tf.keras.layers.Conv2D(filters=64, kernel_size=2, strides=(2,2), activation='elu'),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(64, activation='elu'),
tf.keras.layers.Dense(7*7*64, activation='elu'),
tf.keras.layers.Reshape(target_shape=(7,7,64)),
tf.keras.layers.Conv2DTranspose(filters=32, kernel_size=2, strides=(2,2), padding='same', activation='elu'),
tf.keras.layers.Conv2DTranspose(filters=1, kernel_size=2, strides=(2,2), padding='same', activation='sigmoid')
])
model.compile(optimizer=tf.optimizers.Adam(), loss='mse')
model.summary()9. fit & 결과
model.fit(train_X, train_X, epochs=10, batch_size=256)
import random
plt.figure(figsize=(4,8))
for c in range(4):
plt.subplot(4, 2, c*2+1)
rand_index = random.randint(0, test_X.shape[0])
plt.imshow(test_X[rand_index].reshape(28, 28), cmap='gray')
plt.axis('off')
plt.subplot(4, 2, c*2+2)
img = model.predict(np.expand_dims(test_X[rand_index], axis=0))
plt.imshow(img.reshape(28, 28), cmap='gray')
plt.axis('off')
plt.show()
model.evaluate(test_X, test_X) # loss 0.00625997409224510210. 잠재변수 벡터 확보
latent_vector_model = tf.keras.Model(inputs=model.input, outputs=model.layers[3].output)
latent_vector=latent_vector_model.predict(train_X)
print(latent_vector.shape)
print(latent_vector[0])11. 군집
labels_: 각 데이터가 0부터 9사이의 어떤 클러스터에 속하는지에 대한 정보가 저장cluster_cetners_: 각 클러스터의 중심 좌표가 저장되고, 잠재변수와 마찬가지로 64차원이기 때문에 이 좌표가 각각 무엇을 의미지하는지 직관적으로 알기 어렵다.kmeans.cluster_centers_[0]: 각 클러스터에 속하는 이미지가 어떤 것인지 출력한다.
# 사이킷런의 K-평균 클러스터링 알고리즘 사용, 군집
%%time
from sklearn.cluster import KMeans
kmeans=KMeans(n_clusters=10, n_init=10, random_state=42)
kmeans.fit(latent_vector)
# 군집 결과
print(kmeans.labels_)
print(kmeans.cluster_centers_.shape)
print(kmeans.cluster_centers_[0])12. 시각화
- 출력 이미지의 각 행은 0번 클러스터, 1번 클러스터, …, 9번 클러스터를 나타냄
- 숫자가 다르면서 같은 클러스터로 분류된 이미지들이 문제이다.
- 잠재변수의 차원수를 늘리거나 KMeans()의 n_init을 늘려서 좀 더 분류가 잘 되도록 시도해볼 수 있다.
- 그러나, 여전히 클러스터링 결과를 시각화를 해야 문제가 남고, 이를 시행하려면 2차원 또는 3차원의 잠재변수가 가진 자원을 축소해야 한다.
import random
plt.figure(figsize=(12,12))
for i in range(10):
images=train_X[kmeans.labels_ == i]
for c in range(10):
plt.subplot(10, 10, i*10+c+1)
plt.imshow(images[c].reshape(28, 28), cmap='gray')
plt.axis('off')
plt.show()
13. t-SNE의 개념
- 고차원의 벡터를 저차원으로 옮겨서 시각화에 도움을 주는 방법
k-Means가 각 클러스터를 계산하기 위한 단위로 중심과 각 데이터의 거리를 계산- t-SNE는 각 데이터의 유사도를 정의하고, 원래 공간에서 유사도와 저차원 공간에서의 유사도가 비슷해지도록 학습시킴
SNE는 Stochastic Neighbor Embedding의 약자로, 여기에서 유사도는 확률적(Stochastic)으로 표현됨- t는 t-분포를 나타냄
- t-SNE 알고리즘의 주요 핵심 내용은 고차원과 저차원에서 확률값을 각각 구한 다음, 저차원의 확률값이 고차원에 가까워지도록 학습시키는 것
14. t-SNE 수행
n_components는 저차원의 수, 여기서는 2차원 공간이기 때문에 2learning_rate는 학습률로 보통 10에서 1000사이의 큰 숫자 넣기perplexity는 알고리즘 계산에서 고려할 최근접 이웃의 숫자, 보통 5~50random_state랜덤 초기화 숫자
%%time
from sklearn.manifold import TSNE
tsne = TSNE(n_components=2, learning_rate=100, perplexity=15, random_state=0)
tsne_vector=tsne.fit_transform(latent_vector[:5000])15. 시각화
cmap = plt.get_cmap('rainbow', 10)
fig = plt.scatter(tsne_vector[:,0], tsne_vector[:,1], marker='.', c=train_Y[:5000], cmap=cmap)
cb = plt.colorbar(fig, ticks=range(10))
n_clusters = 10
tick_locs = (np.arange(n_clusters) + 0.5)*(n_clusters-1)/n_clusters
cb.set_ticks(tick_locs)
cb.set_ticklabels(range(10))
plt.show()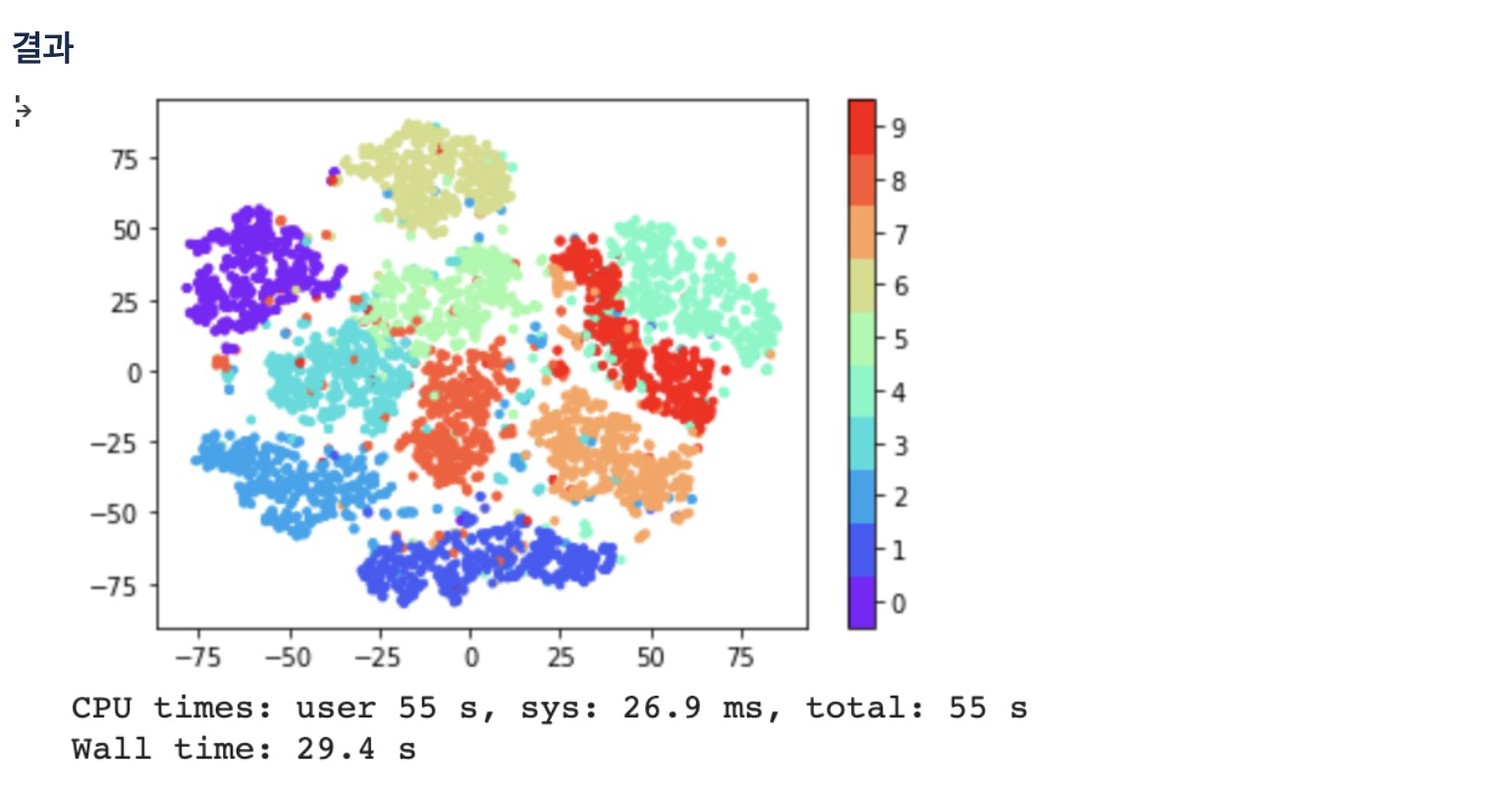
16. perplexity 튜닝
- perplexity가 높아질수록 뭉치는 클러스터도 있지만, 뒤섞이는 클러스터도 보이는 것으로 볼 때 최적의 값을 찾기 위해서는 다른 하이퍼파라미터처럼 여러번의 실험이 필요한 것 같다.
%%time
perplexities = [5, 10, 15, 25, 50, 100]
plt.figure(figsize=(8,12))
for c in range(6):
tsne = TSNE(n_components=2, learning_rate=100, perplexity=perplexities[c], random_state=0)
tsne_vector = tsne.fit_transform(latent_vector[:5000])
plt.subplot(3, 2, c+1)
plt.scatter(tsne_vector[:,0], tsne_vector[:,1], marker='.', c=train_Y[:5000], cmap='rainbow')
plt.title('perplexity: {0}'.format(perplexities[c]))
plt.show()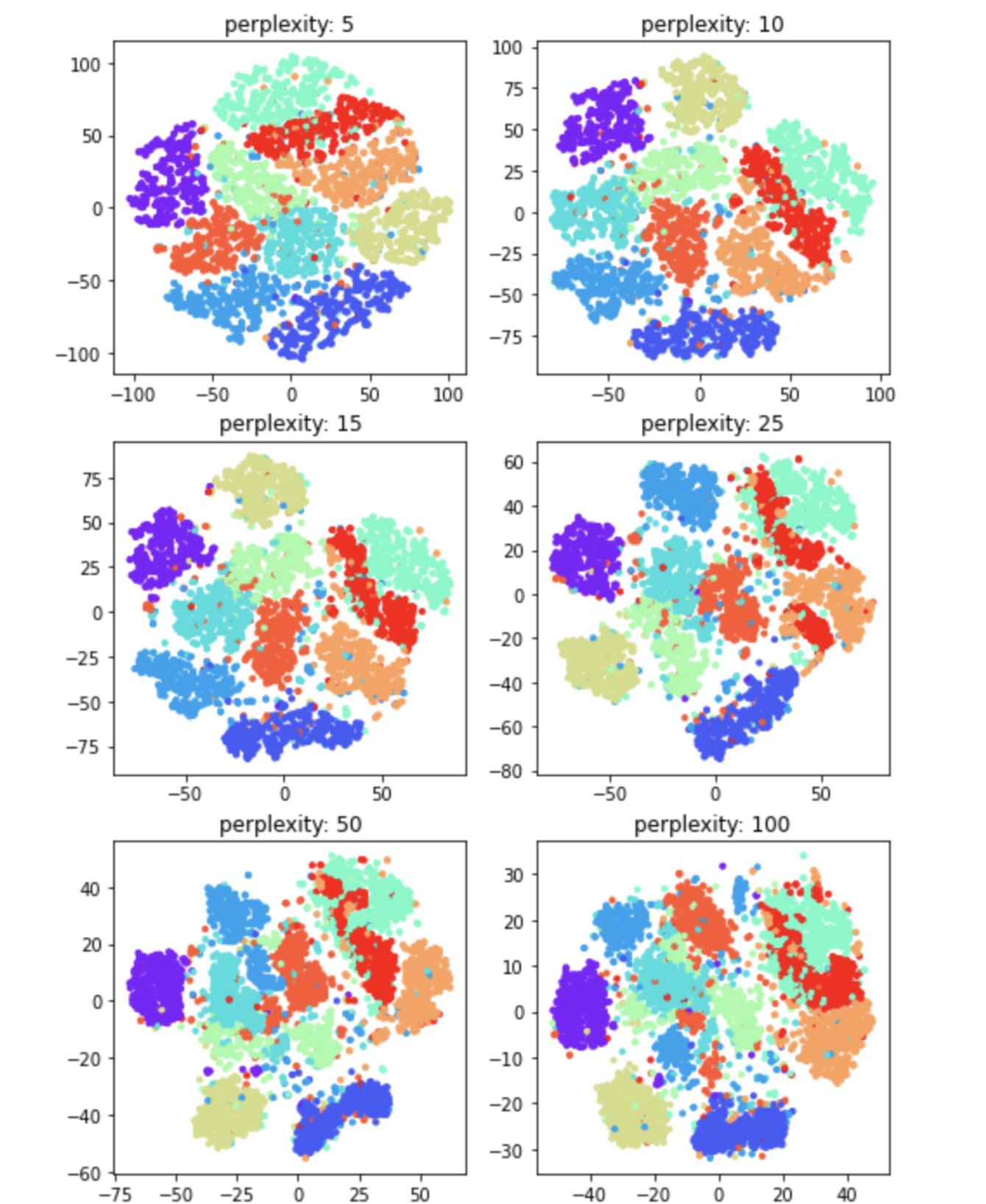
17. t-SNE로 분리된 클러스터 위에 MNIST이미지를 표시
# 약간의 뎁스를 더 가젼간 시각화
from matplotlib.offsetbox import TextArea, DrawingArea, OffsetImage, AnnotationBbox
plt.figure(figsize=(16, 16))
tsne=TSNE(n_components=2, learning_rate=100, perplexity=15, random_state=0)
tsne_vector=tsne.fit_transform(latent_vector[:5000])
ax = plt.subplot(1, 1, 1)
ax.scatter(tsne_vector[:, 0], tsne_vector[:,1], marker='.', c=train_Y[:5000], cmap='rainbow')
for i in range(200):
imagebox = OffsetImage(train_X[i].reshape(28, 28))
ab = AnnotationBbox(imagebox, (tsne_vector[i, 0], tsne_vector[i, 1]), frameon=False, pad=0.0)
ax.add_artist(ab)
ax.set_xticks([])
ax.set_yticks([])
plt.show()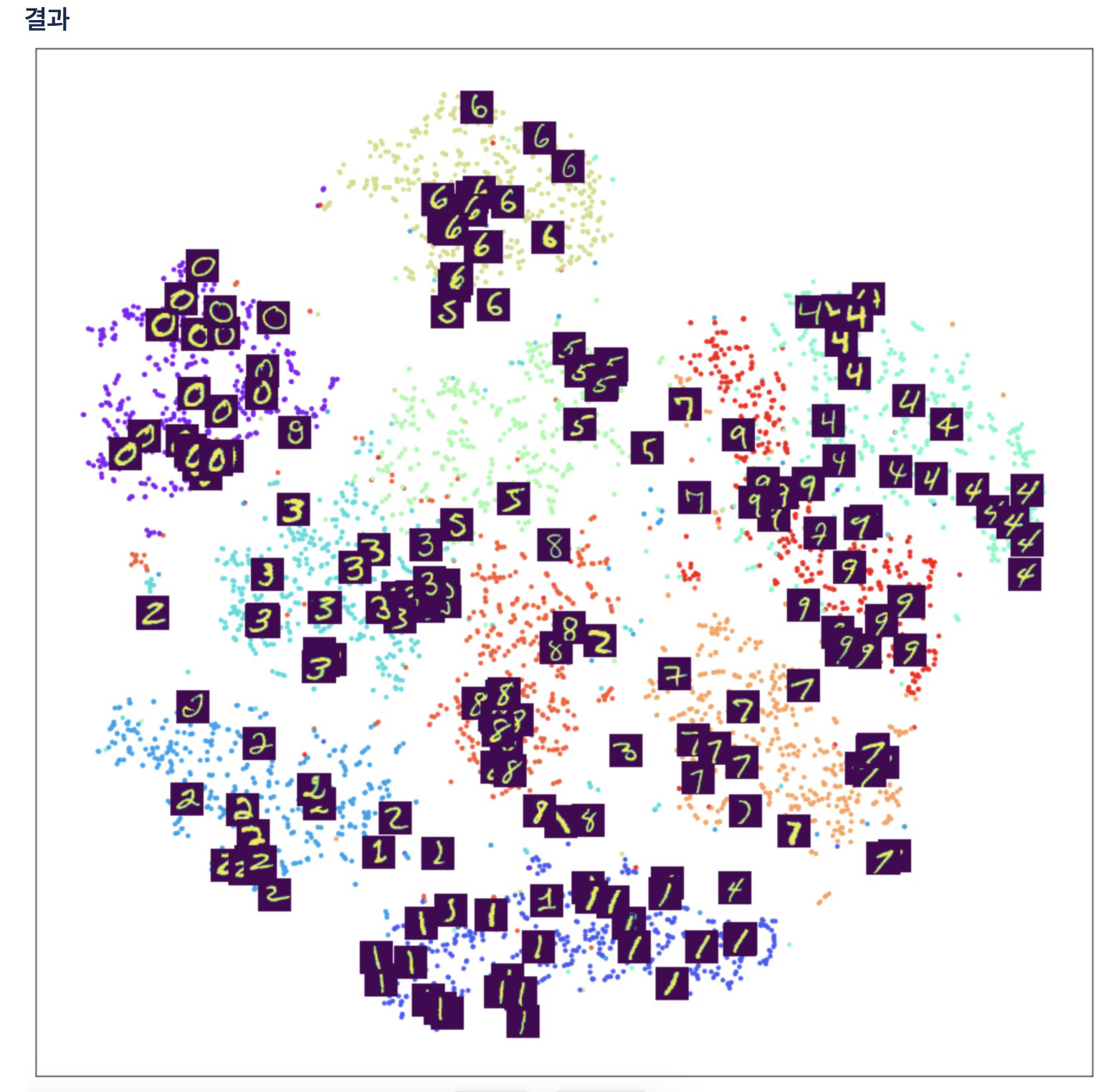
- 추가: 텐서플로우에서 이미지증강(augmentation): https://www.tensorflow.org/tutorials/images/data_augmentation?hl=ko
Reference
1) 제로베이스 데이터스쿨 강의자료
2) https://dschloe.github.io/python/tensorflow2.0/ch9_1_auto_encoder/
