노드 임베딩에 대해 이해하기 위해 CS224W 강의도 참조했습니다…. 알아야 할 것 같아서..
1. Graph Representation Learning
Graph Representation Learning은 그래프의 요소(Node, Link, Graph)를 입력으로 하여 임의의 d차원 벡터로 변환시키는 작업을 말한다. 그 과정에서 모델이 사용되며, 해당 모델은 그래프의 요소를 임베딩 공간으로 매핑시킨다.
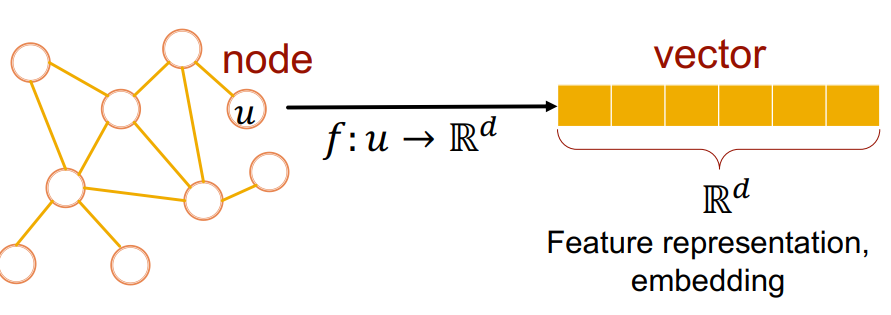
즉, 토큰이라는 이산적인(discrete) 변수를 임베딩 공간으로 맵핑시키듯이, Node Embedding은 유사도를 기준으로 각 노드들을 임베딩 공간으로 매핑시켜 비슷한 노드는 임베딩 공간 내에 근처에서 위치하도록 만드는 기술이다.
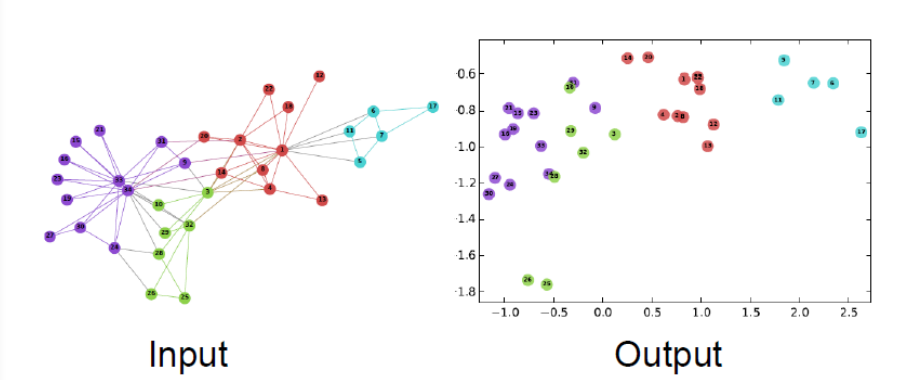
→ 여기서, 노드를 임베딩했을 노드 사이의 임베딩 유사도는 실제 그 네트워크의 유사도를 나타내고, 임베딩은 네트워크의 정보를 인코딩하여 갖게 됨.
2. Node Embedding
- V는 노드 집합, A는 인접 행렬을 의미한다.
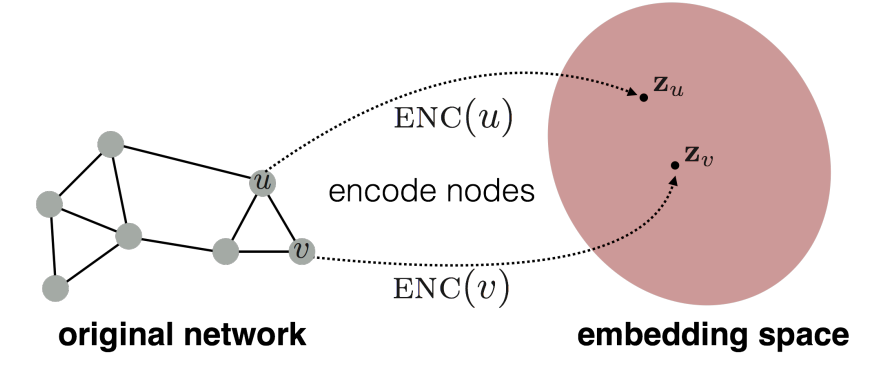
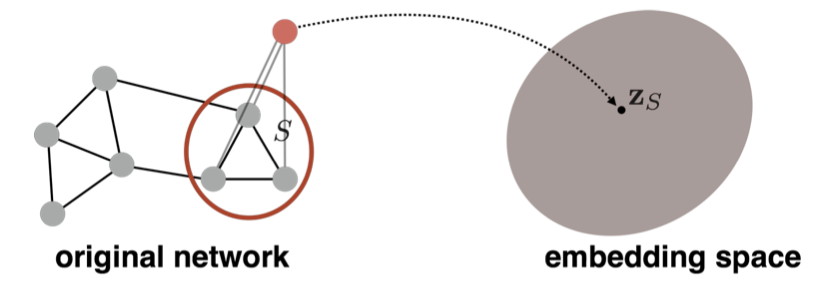
입력값으로 주어지는 그래프는 각 노드가 임의의 인코더를 통과해 임베딩 공간에 위치하는 벡터로 바뀌는 과정이다.
그리고 이 과정은, 그래프에서 유사한 노드들이 임베딩 공간에서 근처에 있도록 매핑하는 것이다. (Word2vec을 알고 있다면, 꽤 이해가 빠를 것이다.)
위 그림에 대해 수식을 표현하면 다음과 같다.
그래프에서 두 노드 u, v의 유사도는 임베딩 공간에서 두 벡터 의 유사도로 근사되어야 한다. (임베딩 공간의 유사도로 내적 사용)
Framework
노드 임베딩 과정은 다음과 같다.
- 인코더가 노드를 임베딩 공간으로 매핑해 벡터를 생성한다.
- 고차원 그래프 구조 → 저차원 임베딩 공간에 매핑, 수치적으로 표현이 가능한 벡터를 생성
- 그래프 내 구조적 정보를 학습해 유사한 노드들이 가까운 벡터로 매핑되도록 함.
- 적용 예시 : Node2Vec / Deepwalk
- 노드 유사도 함수를 정의하고, 이를 통해 그래프에서 노드 간 유사도를 측정한다.
- 그래프 상에서 서로 유사한 노드가 임베딩 공간에서도 가깝게 위치하도록 학습한다.
- 노드 간 유사도를 측정하기 위한 기준 필요
- 디코더가 매핑된 벡터에 대해 유사도를 측정한다. (내적 사용, inner product)
- 인코더로부터 생성된 임베딩 벡터가 원래 그래프 상의 유사도를 얼마나 잘 반영하는지 확인
- 디코더는 그래프의 구조적 관계를 임베딩 벡터에서 복원하려고 함.,
- 2와 3에서 측정된 유사도가 비슷해지도록 인코더의 파라미터를 최적화한다.
- 인코더가 원래 그래프 구조를 최대한 잘 학습하도록 파라미터를 업데이트
- 디코더가 예측한 유사도가 원래 그래프의 유사도와 비슷해지도록 학습
Shallow Encoding

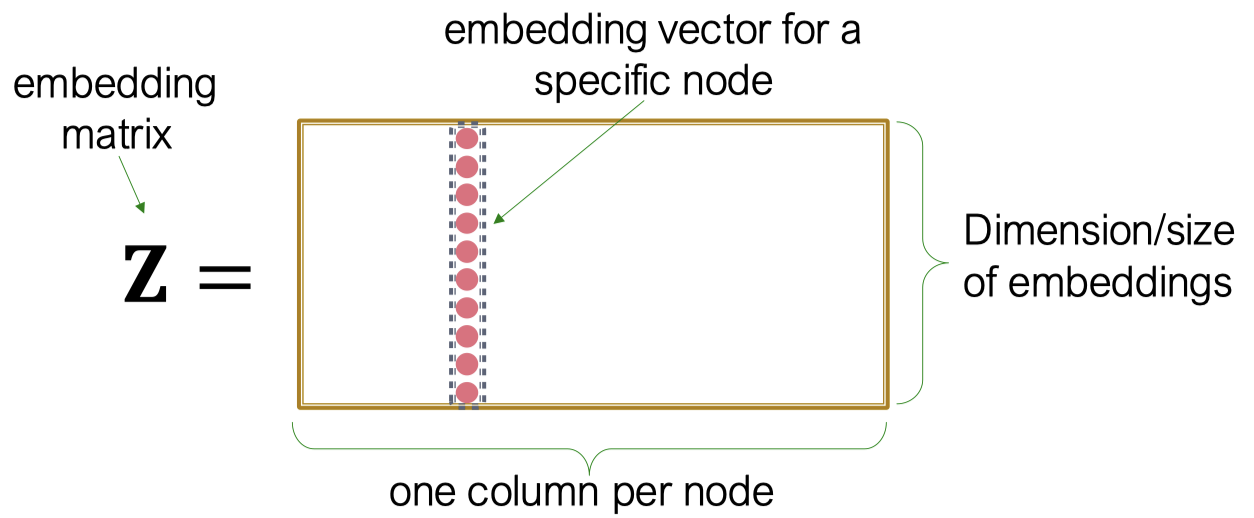
(위 두 그림은 같은 그림....)
가장 단순한 인코딩 방식은 인코더가 단순히 embedding-lookup하는 것이다.
embedding-lookup이란 룩업 테이블에서 입력으로 주어진 노드 인덱스의 열만 출력하는 것을 의미한다.
: 각 컬럼이 노드 임베딩인 행렬로 학습해야 하고, 최적화해야 하는 목표
: Indicator vector (특정 조건을 만족하면 1, 아니면 0)
이 방법은 각 노드가 개별적인 임베딩 벡터를 갖게 되는데, 각 노드의 임베딩을 직접 최적화할 수 있다는 장점이 있다.
그렇지만, 노드의 수가 많아지게 될 경우, 가지고 있어야 하는 룩업 테이블이 기하급수적으로 커지게 되는 단점이 존재한다.
구체적인 문제점은 다음과 같다.
- 국소 (local) 정보만 반영
- 그래프의 전역적 구조 정보나 멀리 떨어진 노드 간의 관계를 잘 반영하지 못함
- 선형 변환 또는 간단한 비선형 함수로 임베딩을 생성하기에, 복잡한 관계를 학습하기가 어려움
- 학습된 임베딩 벡터가 고정되어 있어, 그래프에 새로운 노드가 추가되거나 기존 노드가 변경되면 유연하게 대응하기 어려움
- 각 노드를 독립적으로 임베딩하는 경우가 많아, 이웃 노드 간의 관계나 속성 정보를 충분히 반영하지 못함. (각 노드의 파라미터를 공유하지 않음)
- 그래프 크기가 커질수록 학습 시간 및 저장 공간 요구량이 기하급수적으로 증가
Random Walk
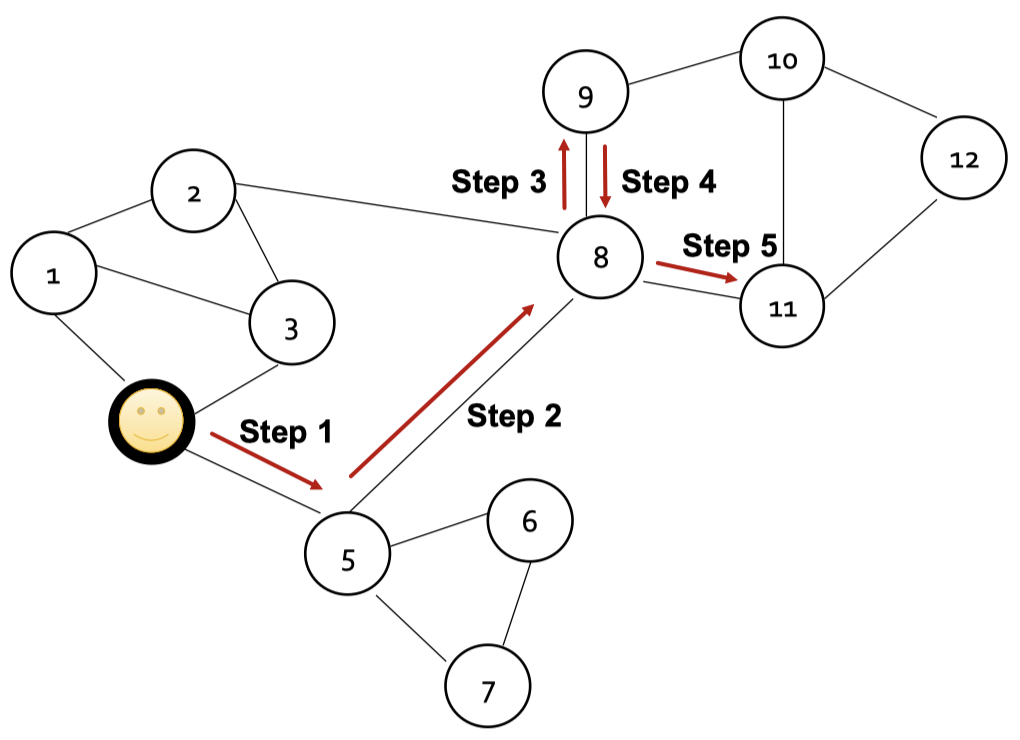
랜덤 워크는 그래프의 노드에서 다른 이웃으로 순차적이자 임의로 이동하는 것을 말한다. 그래프의 시작점이 주어지면, 시작점의 이웃을 무작위로 선택하고, 그 이웃으로 이동한 다음 이 과정을 반복한다.
만약 두 랜덤 워크가 있을 때 두 노드 가 함께 등장하는 빈도가 높다면, 두 노드는 가깝게 위치한다고 볼 수 있다.
→ : 두 노드가 함께 등장할 가능성
랜덤 워크의 과정
- 노드 로부터 시작하는 어떤 랜덤 워크 이 있을 때, 이 랜덤 워크가 노드 를 지날 확률 를 추정한다.
- 이 확률값을 토대로 임베딩을 최적화하고, 임베딩 공간에서 유사도는 의 내적이다.
랜덤 워크는 다음의 장점을 가집니다.
- 표현력(Expressivity)
- 국소적인 이웃 정보와 높은 차원의 이웃 정보를 모두 통합하는 노드 유사도에 대한 확률적 정의이기 때문
- 효율성(Efficiency)
- 학습 시 모든 노드 쌍을 고려할 필요 없이 랜덤 워크에서 함께 등장하는 노드 쌍만 고려하면 되기 때문
Negative sampling → Random Walk의 문제를 개선하기 위한 방법
랜덤 워크는 계산 비용이 매우 높다는 문제점이 있습니다. 이를 해결하기 위해 네거티브 샘플링을 사용하는데, 이 경우에는 전체 노드에 대해 내적을 계산하는 대신, 노드 와 이웃하지 않는 노드 개를 샘플링하여 일종의 log loss를 계산한다.
여기서 는 시그모이드 함수로, 소프트맥스에 비해 계산적으로 빠름.
k개의 노드는 각 degree에 비례해 확률을 계산하여 샘플링을 진행한다. (보통 5~20의 값을 선정)
k의 값이 클수록, 더 강건한 추정을 하지만, 이웃하지 않은 노드에 대해서는 편향적인 결과가 나올 수 있음.
마지막으로 네거티브 샘플링을 적용한 손실 함수에 SGD를 적용하여 임베딩을 최적화한다.
Node2Vec
랜덤 워크 방식을 일반화한 방식으로서, 네트워크 내 비슷한 이웃을 가진 노드를 피처 공간에 가깝게 임베딩시키는 것을 목적으로 한다. 그리고, 이 목적을 달성하기 위해 Downstream 예측 task들과 최대한 독립적인 최대 우도 최적화 문제로 설정한다.
Node2Vec은 이웃 노드 집합 를 찾을 때, 비교적 유연한 랜덤 워크 전략 을 이용해 노드 임베딩에 더욱 풍부한 정보를 인코딩한다. 이를 위해 Biased Random Walk를 활용하는데, 이는 각 네트워크의 국소적 측면과 전역적 측면을 바라볼 때 발생하는 Trade-off의 균형을 맞출 수 있는 유연성을 제공한다.
Trade-off of BFS, DFS
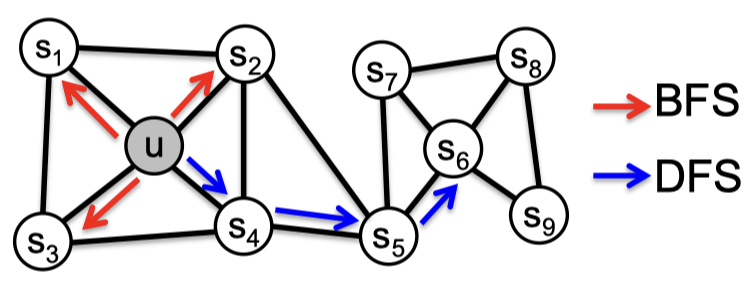
이 과정에서 국소적인 미시적 관점에서 이웃은 다음과 같습니다
전역적이고 거시적인 관점 (DFS)는 조금 다름
Biased Random Walk
고정 길이의 편향된 랜덤 워크는 2개의 파라미터를 사용한다.
: 이전 노드로 돌아갈 확률을 정하는 파라미터
: 직전 노드에서 먼 노드로 갈 확률을 정하는 파라미터 (DFS, BFS의 비율을 정하는 개념)
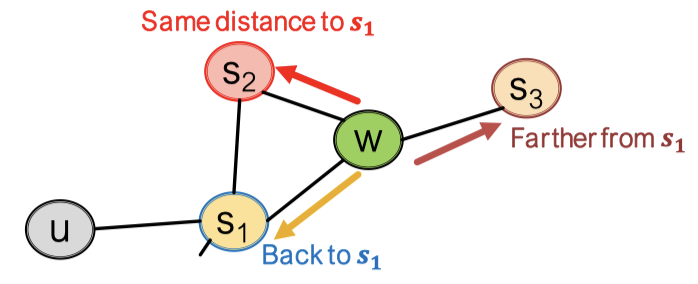
위 이미지의 상황에서 에서 로 도착했다고 가정하면, 3가지의 경우의 수가 존재한다.
- 로 돌아가기 →
- 거리가 동일한 로 이동 → 1
- 로 이동하기 (거리가 더 멀어짐) →
실제 어떤 노드로 이동하는지는 에 의해 결정됨.
이 모든 확률값은 정규화되지 않음. BFS처럼 행동하기 위해서는 가 낮아야 하고, 의 값이 낮아지면 더 먼 곳으로 이동할 확률이 높아져 DFS처럼 행동하게 됨.
즉, 에 따라 랜덤 워크가 편향적으로 진행된다.
Node2Vec 학습 알고리즘
- 랜덤 워크 확률 계산
- 노드 에서 시작하는 길이 의 랜덤 워크 을 실행함
- SGD를 이용해 Node2Vec의 목적 함수를 최적화함
이 학습 과정은 선형적인 시간 복잡도를 가져 빠르게 진행되고, 각 순서를 병렬처리할 수 있어 더 빠르게 진행가능하다.
전체 그래프 임베딩
이 과정에서 수행하는 것은 그래프 G나 그 서브그래프를 임베딩하는 것이다.
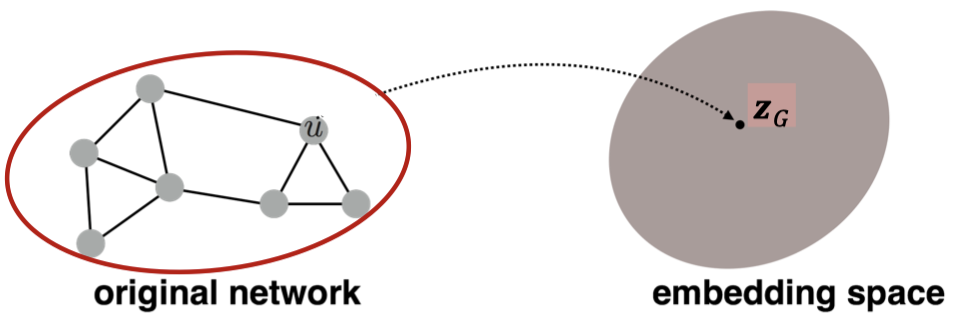
노드 임베딩을 사용해 그래프 G나 서브그래프에 적ㅇ용하고, 그래프나 서브그래프의 노드 임베딩을 모두 더하거나 평균을 계산한다.
또다른 방법으로는, 가상 노드를 사용하는 것인데, 임베딩하고자 하는 그래프나 서브그래프의 모든 노드와 연결된 가상 노드를 생성한다. 그리고, 여기에 기본적인 임베딩 방식을 적용한다.
행렬 분해와 노드 임베딩
노드 임베딩을 살펴보면, 가까이 있는 두 노드 에 대해 노드 임베딩 를 최대화하는 목적함수를 통해 임베딩을 하게 된다. 임베딩 행렬 는 임베딩 차원 d에 대해 의 크기를 가진다.
가장 간단한 노드 유사도는 노드 간 연결정보이기 때문에, 는 Adjacement Matrix에서 와 같다고 할 수 있음.
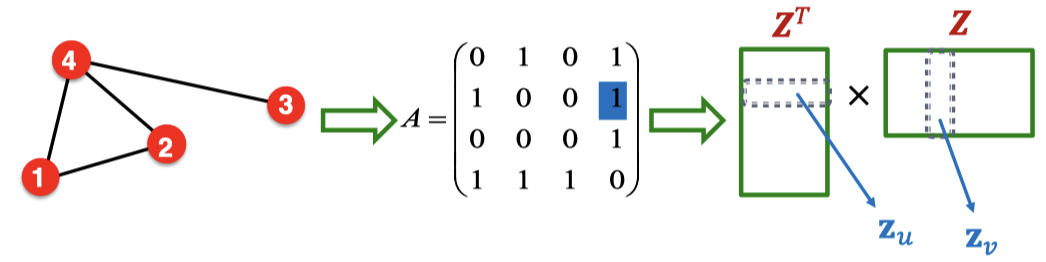
임베딩 차원 d는 일반적으로 노드의 수보다 작고, 인접 행렬 A를 완벽하게 로 분해하게 만드는 Z를 계산하는 것도 불가능하기에, Z를 근사적으로 학습하도록 만든다.
위 식대로 의 L2 Norm을 최소화하는 Z를 찾도록 최적화를 수행한다. 단, 최근에는 소프트맥스를 더 많이….
→ 엣지간 연결로 정의한 노드 유사도를 사용한 내적 디코더는 인접 행렬 A에 대한 행렬 분해와 같음을 알 수 있다.
Deep Encoding
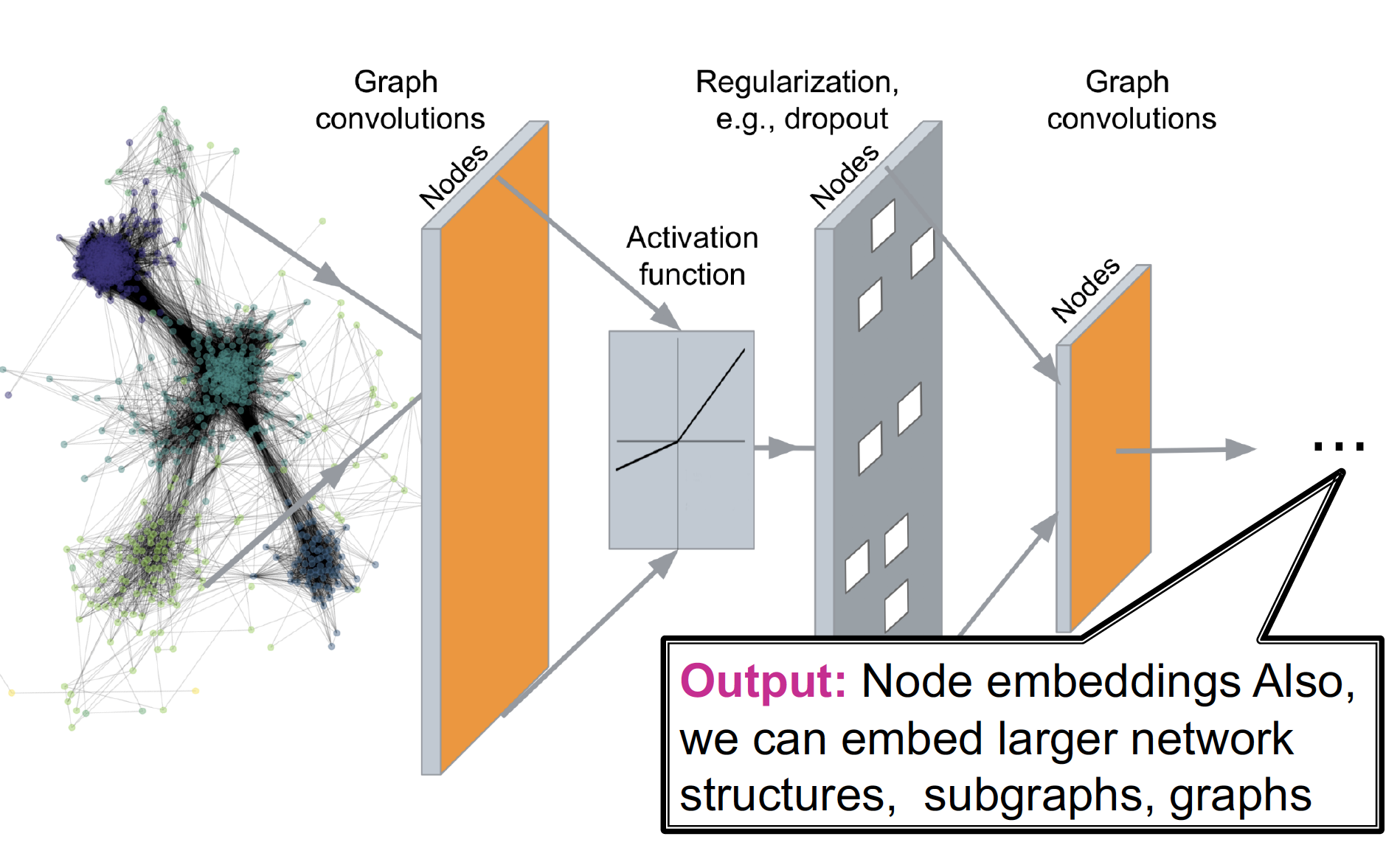
Deep Encoding에는 대표적으로 GNN이 있다.
→ 이 과정에서는, 점이 이웃과의 연결에 의해 정의되는 것을 전제로, 이웃들의 상태를 이용해 각 점의 상태를 업데이트하고, 마지막 상태를 통해 예측을 수행한다.
바로 그 마지막 상태가 Node Embedding이다.
이 모델은 Shallow Encoding의 문제점을 개선할 수 있다.
- Deep encoding은 local, global 정보를 모두 학습할 수 있다.
- 비선형적, 복잡한 데이터에 대해 학습이 가능하다.
- 새로운 데이터에 대해서도 유연하게 적응이 가능하다
- 노드 간의 상호작용 및 관계를 설명하기에 용이하다.
- 모델 크기를 효율적으로 조정할 수 있어서, 저장 공간의 문제가 적다.
→ 단, Encoder 구조는 랜덤 워크 기반이 아닌, CNN, RNN 등의 딥러닝 방법론을 사용해서 다층 비선형 구조를 구성한다.
참조 사이트
https://velog.io/@tobigsgnn1415/Node-Embeddings
https://otzslayer.github.io/cs224w/2023/06/04/cs224w-03.html
