시계열 방법론 : Box-jenkins 방법론

• Box-jenkins 방법론 : 시계열 모형의 통계이론
  • 위키 설명 : 박스-젠킨스(Box–Jenkins) 방법은 자동회귀이동평균(ARMA) 또는 자동회귀누적이동평균(ARIMA) 모델을 적용하여 시계열 과거 값에 대한 시계열 모델 최적합을 찾는다
• Box-jenkins 방법의 3 단계 모델링 방식

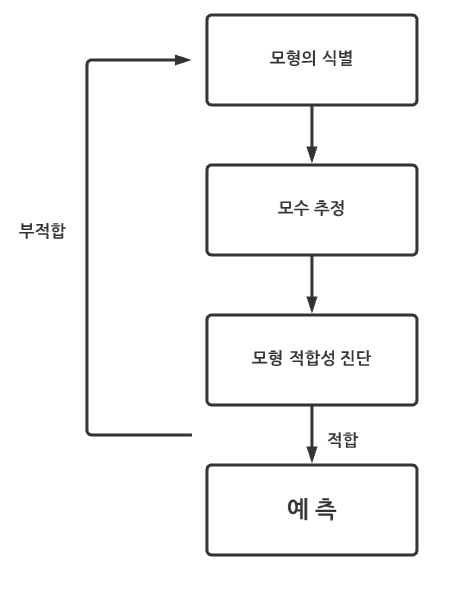
1. 모델 식별 및 모델 선택(Model identification and model selection)

• 시계열의 정상성((stationary)을 확인하고 종속 계열의 계절성을 식별한다.(=모델링해야 할 중요한 계절성이 있는지 확인 & 필요한 경우 계절성 차분)
• 시계열의 자기상관(ACF) 및 부분자기상관(PACF) 함수의 플롯을 사용하여 AR 모형의 p값 또는 MA 모형의 q값을 몇으로 할지 결정한다.

2. 파라미터 추정(Parameter estimation)

• 계산 알고리즘을 사용하여 선택한 ARIMA 모델에 가장 적합한 계수를 찾는다. 가장 일반적인 방법은 최대우도추정법 또는 비선형 최소제곱추정을 사용한다.

3. 통계 모델 검증(Statistical model checking)

• 추정 모델이 고정 일 변량 프로세스의 사양을 따르는지 여부를 테스트하여 통계 모델 확인.
• 특히, 잔차는 서로 독립적이어야 하며 시간에 따른 평균 및 분산에서 일정해야 한다. (시간에 따른 잔차의 평균 및 분산을 플로팅하고 Ljung-Box 테스트를 수행하거나 잔차의 자기 상관 및 부분 자기 상관을 플로팅하면 잘못된 사양을 식별하는 데 도움이 된다.) 추정이 부적절하면 1단계로 돌아가서 더 나은 모델을 만들어야 한다.

Ljung-Box 테스트(링크)

• 잔차가 자기상관이 있는지 테스트 = 잔차가 독립인지 테스트
• 가설
  • $H_0 :$ The data are independently distributed (i.e. the correlations in the population from which the sample is taken are 0, so that any observed correlations in the data result from randomness of the sampling process).
  • $H_1 :$ The data are not independently distributed; they exhibit serial correlation.
  • 즉, p-value값이 유의 수준보다 작다면 $H_0$ 를 기각하여 ⇒ 잔차가 자기상관이 있다고 해석 가능