벡터화한 A, B의 유사도를 구하는 방법에는 유클리디안 유사도로 대표되는 거리 기반 유사도와
코사인 유사도로 대표되는 각도 기반 유사도가 있다.
각도 기반 유사도와 거리 기반 유사도는 언제 사용해야 좋은지 알아보자.
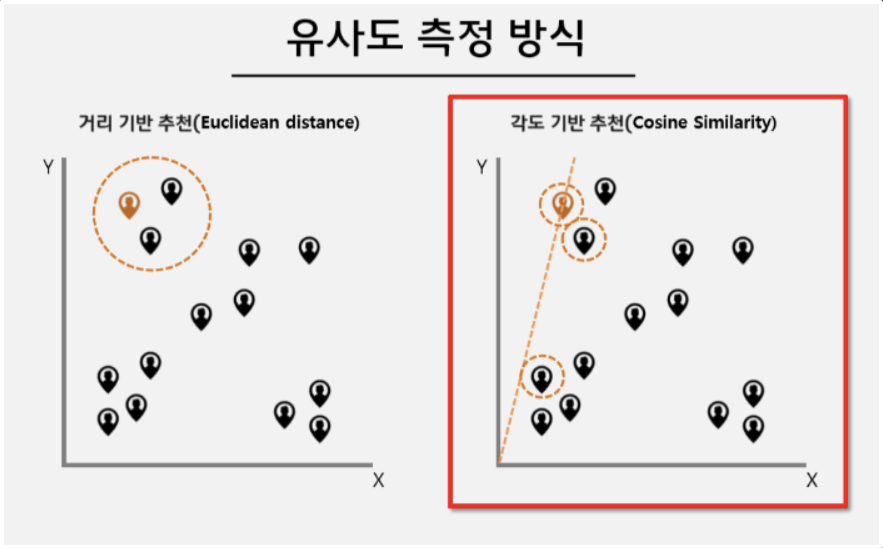
1. 거리 기반 유사도
위 그림 중 좌측 그림을 보면 거리 기반 유사도는 좌표를 기준으로 생각했을때 비슷한(혹은 가까운) 좌표에 있는 점들이 유사도가 높다고 측정된다.
2. 각도 기반 유사도
위 그림 중 우측 그림을 보면 각도 기반 유사도는 좌표를 기준으로 생각했을때, x축과 (0, 0)에서 좌표까지 이르는 점선 주변에 있는 점들이 유사도가 높다고 측정된다.
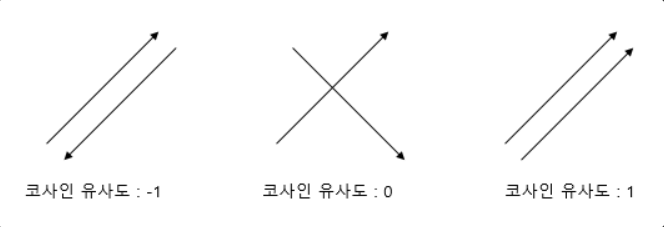
아래 그림은 벡터 간의 코사인 유사도 값을 설명해주고 있다.
쉽게 설명하면, 평행(=기울기가 같은)을 이루고 방향이 같은 벡터간의 유사도가 가장 높다.
그렇다면 언제 거리 기반 유사도를 사용하고 언제 각도 기반 유사도를 사용해야 할까?
가장 쉬운 판단 기준은 스케일의 차이가 크냐? 안크냐? 로 판단하면 된다. (다른 판단 기준도 있을 수 있음)
- 스케일 차이가 크지 않다 -> 거리 기반 유사도(유클리디안 유사도)
- 스케일 차이가 크다 -> 각도 기반 유사도(코사인 유사도)
- (참고) 혹은, 거리 기반 유사도와 각도 기반 유사도의 평균값으로도 해볼 수 있다
(예시)
책A, 책B가 있을때
책A는 : 게임, 액션 이라는 단어가 각각 1개씩 2단어로 이루어져있고
책B는 : 게임, 액션 이라는 단어가 각각 1,000개씩 2,000단어로 이루어져있다고 할 때,거리 기반으로 두 책의 유사도를 측정하면 (1,1)과 (2,000, 2,000)사이의 거리는 큰차이가 나기때문에
두 책의 유사도는 낮다고 말할 수 있지만, 각도 기반으로 두 책의 유사도를 측정하면 기울기가 같고 방향이 같기 때문에 두 책의 유사도는 매우 높게 나타난다.
단어량의 차이는 있지만 책A와 책B는 각각 게임이라는 단어와 액션이라는 단어가 50%비중을 차지하기때문에 매우 유사한 책이라고 볼 수 있는데 거리 기반으로 유사도를 측정하였을 경우 유사하지 않다라는 결과가 나올 수 있다.
따라서, 스케일 차이가 크게 날때는 각도 기반 유사도를 사용하는 것이 더 좋은 경우가 많다.
