궁금증이 생기게 된 계기
- 모델의 성능을 평가하는 F1-score는 Precision과 Recall의 조화 평균을 사용하는 것을 보고 어떤 상황에 어떤 평균을 써야하는지에 대한 궁금증이 생기게되어 이 글을 포스팅하게 되었습니다.
1. 산술평균
- 일상 생활에서 가장 많이 사용하는 평균
- 각 요소의 총 합을 갯수로 나눈 것
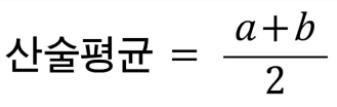
2. 기하평균
- 각 요소를 곱한후 그 값에 루트를 씌운 값
- 일반적으로 성장률의 평균 등 상승률과 하락률을 활용한 계산에 유용하게 쓰임
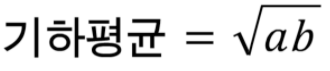
예를 들어 1,000원의 주식이 10% 상승 후 10% 하락 했을 경우 산술적인 개념만 본다면 상승 +10% 하락 -10%로 ±10%이기 때문에 직관적으로 잘못 생각하여 가격 변동이 없다고 착각할 수 있습니다.
하지만, 1,000원이 10% 상승하면 → 1,100원이 되고 1,100원이 10% 하락하면 → 990원이 됩니다.
위 내용처럼 1,000원 짜리 주식이 990원이 되는 것을 상승률 10% 와 하락률 10%에 대한 기하 평균을 활용하여 계산해줄 수 있는데요.
수식으로 표현해보면 = 0.99 → 1,000원 0.99원 = 990 라는 결과를 얻을 수 있습니다.
3. 조화평균
- 각 요소의 역수를 산술평균한 후 그 값을 다시 역수로 변환한 것
- 왕복속력을 계산할때, F1-Score 계산시 주로 사용
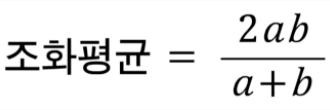
예를 들어 두 지점 A, B에 대하여 갈때는 시속 10Km/h, 올때는 시속 20Km/h로 왕복했다면,
평균속력은 조화평균인 13.33Km/h가 됩니다.
= = =
4. 산술평균 ≥ 기하평균 ≥ 조화평균
-
수식
-
(심화1) 산술평균 vs 기하평균 vs 조화평균 간의 관계
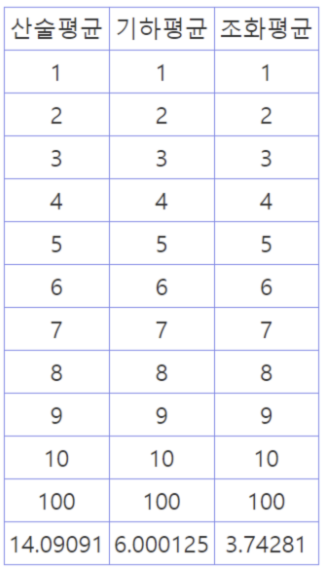
- 각 평균의 종류의 상대적인 크기는 산술평균 > 기하평균 > 조화평균
- 1~10까지의 평균값은 5.5인데 단순 100이라는 이상치가 끼어들면서 산술평균이 가장 많이 상승함
- 이는 평균의 대표성을 띄고 있지 못하다고 판단할 수 있음
- 따라서, 상황에 따라서 적합한 대표성을 띄는 평균을 사용해야할 것이다.
-
(심화2) 조화평균 및 F1-score의 기하학적 의미
- 아래 그림에서 서로 다른 길이의 A, B의 끝에서 다른 쪽의 base라인으로 선을 내렸을때, 만나는 점의 길이

- F1-score의 기하학적 의미
- 기하학적으로 봤을때 단순 평균이라기보다는 작은 길이 쪽으로 치우치게된, 그러면서 작은 길이 보다도 작은 평균이 도출됨
- 이렇게 조화평균을 이용하면 산술평균을 이용하는 것보다, 큰 비중이 끼치는 bias가 줄어든다고 볼 수 있음
- 즉, 아래 그림에서는 Precision보다 큰 길이(=비중)을 차지하는 Recall이 끼치는 bias가 줄어든 값으로 F1-score를 얻게됨

- 아래 그림에서 서로 다른 길이의 A, B의 끝에서 다른 쪽의 base라인으로 선을 내렸을때, 만나는 점의 길이
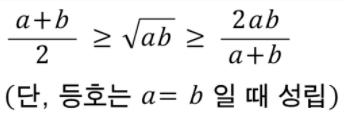

F1 score와 조화평균이 뭔가 찾아보다가 오게 되었습니다.
다만, 조화 평균과 F1 score의 기하학적 의미 그림이 밑에 레퍼런스로 적어 주신 티스토리 쪽 그림과
다른 것 같습니다. 조화 평균 공식 상으로는 티스토리쪽이 맞는거 같기도 한데...
(최소값보다는 조화 평균이 크게 나와야 맞지 않을까 싶네요. 그림의 B, Precision)