목표
- 차원축소 알고리즘인 PCA알고리즘에 대해서 정리하고자 함
- PCA를 왜 쓰는지 그리고 쓰면 머가 좋은지에 대해서 결론적인 얘기만 하고자함
(질문) PCA를 왜 사용하셨나요??
흔히, PCA 알고리즘을 차원축소 알고리즘으로 알고있다.
그렇기 때문에 면접때 PCA를 왜 사용했냐고 물어봤을때,
단순히 차원을 축소하기 위해서 썻다고 답변하는 경우가 허다하다.
(이 답변은 30점 정도 줄 수 있는 답변이다.)
PCA를 사용하면 아래와 같은 문제를 해결할 수 있다고 답변해야 더 좋은 답변이다.
- 다중공선성 문제 해결
- 차원의 저주 문제 해결
- 차원을 축소해주기때문에 사람이 쉽게 관찰하고 이해할 수 있는 2차원으로 데이터들을 보여줄 수 있음
- 차원을 축소해주기때문에 계산량이 줄어들어 컴퓨팅 파워를 효율적으로 사용할 수 있다.
PCA는 어떤 알고리즘인가?
PCA는 차원축소 알고리즘으로 생각하기보다는 기존 변수를 조합해 새로운 변수를 만드는 변수 추출(Feature Extraction) 기법 이라고 알고있으면 좋다. 이때, 변수 선택(Feature Selection) 기법과 용어가 헷갈릴 수 있는데
1) 변수 선택(Feature Selection) : 있는 변수 중 결과값을 잘 표현할 수 있는 변수를 (있는 변수들 중에서) 단순히 고르는것
2) 변수 추출(Feature Extraction) : 변수들을 조합해 새로운 변수를 만들어 결과값을 잘 표현하는 방법
좀 더 스마트하게 PCA 알고리즘을 설명해보면, 기존의 변수들을 선형 결합(linear combination) 하여 새로운 변수를 만들어 내는 기법이라고 할 수 있겠다.
그렇다면 PCA를 통해서 어떻게 1) 차원의 저주 문제와 2) 다중공선성 문제를 해결할 수 있을까요?
1) 차원의 저주 문제
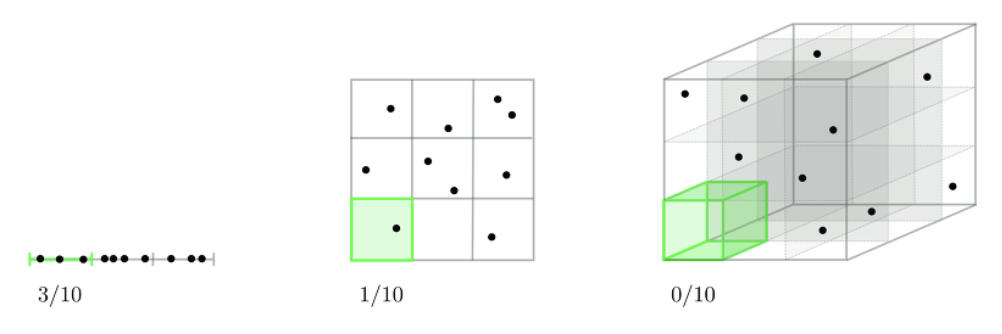
차원의 저주란 차원이 증가할수록 => 데이터를 표현할 수 있는 공간은 커지지만 데이터의 갯수는 그대로이기 때문에 데이터의 밀도가 희소해지는 현상이다.
따라서, 차원이 커진만큼(=데이터를 표현할 공간이 커진만큼) 데이터량도 많아야 학습이 잘된다. 차원은 커졌지만 데이터의 양이 부족하다면, 차원의 일부 공간에 제한되서 혹은 공간별로 소수의 데이터만을 설명하기 때문에 학습된 것만 잘 맞추는 과적합(Overfitting) 문제가 발생할 수 있다.
따라서, PCA 알고리즘으로 차원을 줄여주게 된다면 데이터가 적은 차원에서 밀도있게 표현되기 때문에 차원의 저주 문제를 해결할 수 있다.
2) 다중공선성 문제
다중공선성 문제는 변수들간의 상관관계가 높을때 문제가 발생한다.
유식하게 표현해보자면 독립변수들 간의 강한 상관관계가 나타날때 다중공선성 문제가 발생한다.
그렇다면, 다중공선성이 왜 문제냐?
회귀분석의 가정(전제 조건)인 변수들간의 상관관계가 높으면 안된다는 가정을 위배하게된다.
상관계수가 높다면 X1, X2라는 변수가 있을때 오롯이 X1이 Y값에 어느정도 영향을 미쳤는지 X2값은 얼마나 영향을 미쳤는지 알 수 없다. 따라서 X1, X2에 붙게되는 계수(=회귀계수)를 신뢰할 수 없게된다.
따라서, PCA 알고리즘을 사용하게 되면 주성분 PC1과 PC2를 찾는 과정에서 두 변수가 직교해야하기때문에 두 변수 사이의 상관관계가 0으로 나타나 다중공선성 문제를 해결할 수 있게 된다.
