Loss Functions

Scores를 $f(x,W)=Wx$ 라고 할 때,

SVM loss

$L_i=\sum_{j \neq y_i}max(0,\ s_j-s_{y_i}+1)$

$L={1\over N} \sum_{i=1}^{N}L_i$

즉 1만큼의 margin을 두고 실제 값에서 1보다 큰 값만큼 멀어지면 그때 그 값을 loss로 정의한다는 의미를 갖는다.

최종적으로 cat, car, frog의 $L_i$값을 계산하여 평균을 내면 최종 loss를 구할 수 있다.

Q1. SVM loss $L_i$ 의 범위는?

0 ~ inf

Q2. W값을 0에 가까운 값으로 초기화하는 초반에는 값이 어떻게 되는가?

max(0, 0-0+1) = 1 이 되어 $L_i$ 값이 모두 1이 될 것이다.

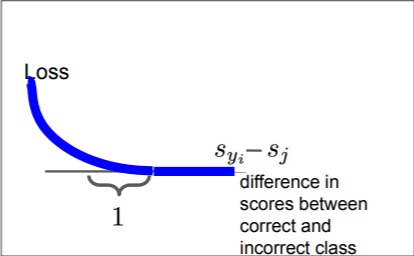
Q3. $L_i=\sum_{j \ne y_i}max(0,\ s_j-s_{y_i}+1)^2$를 사용하면 어떻게 되는가?

기존 선형식과 다르게 비선형성을 가지므로 기존과 다른 값을 얻을 것이다.

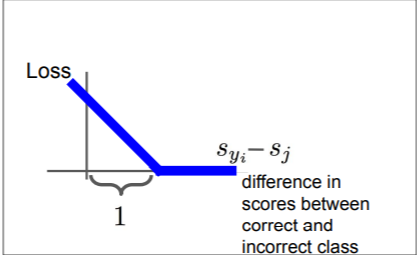
Q4. L=0이 되는 W는 unique한가?

그렇지 않다. 무한대만큼 존재한다. W=2W=...=nW
그렇다면 W 와 2W중 어떤 것을 골라야 하는가?

이때 사용하는 방법이 Regularization이다.

Regularization

$L(W)={1\over N}\sum_{i=1}^N L_i(f(x_i,\ W),\ y_i)+\lambda R(W)$

우변의 왼쪽부분은 Data loss로 training data에 대한 loss를 의미한다. 그리고 오른쪽 부분은 Regulaization부분으로 모델이 training data에 너무 fit하지 않도록, W값을 조정하는 역할을 한다. 즉, 모델이 너무 복잡하지 않도록 규제하는 역할을 한다.
$\lambda$는 hyperparameter이다.
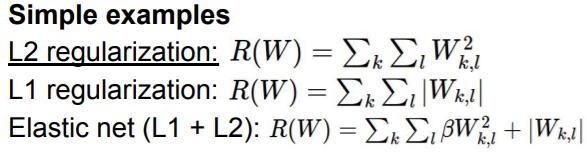L2 regularization은 weights를 spread out하려는 특성을 가진다.

Softmax classifier (Multinomial Logistic Regression)

Softmax Function

$P(Y=k\ |\ X=x_i)={e^{s_k}\over \sum_j e^{s_j}}$

$s=f(x_i;\ W)$

$L_i=-logP(Y=y_i\ |\ X=x_i)=-log({e^{s_{y_i}}\over \sum_je^{s_j}})$

Q1. Softmax loss Li의 범위는?

-log함수의 그래프이고 log의 인자가 0-1의 범위를 가지므로 loss값인 Li는 0~inf의 값을 가질 것이다

Q2. 초기에 s값들을 0으로 초기화한다면 Li는 어떻게 되는가?

$e^0=1$이므로 3개의 종류로 나누는 classifier인 경우 $-log(1/3)=log(3)$이 될 것이다.

Softmax vs SVM

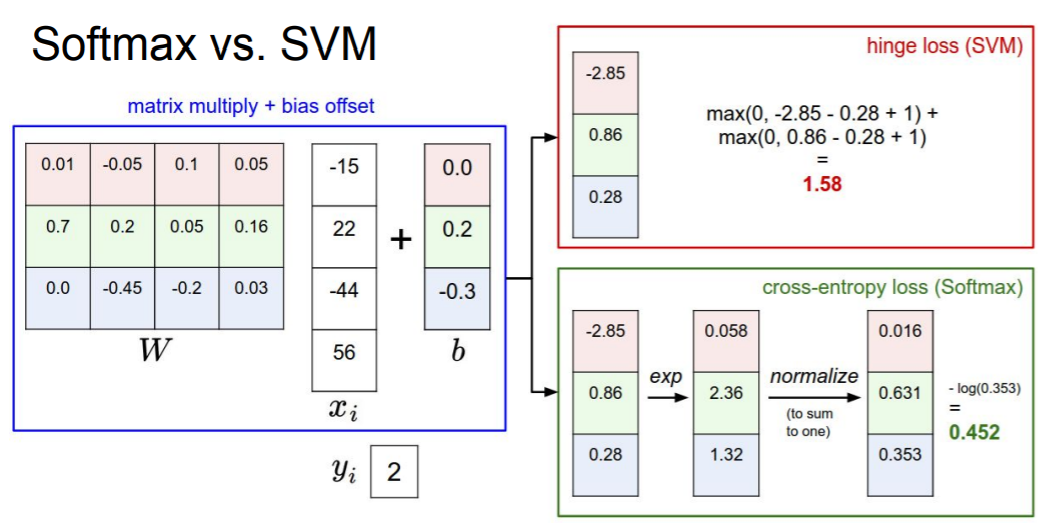
SVM은 1만큼의 margin을 두고 있기 때문에 correct score을 임의로 조금 변경하더라도 loss값의 차이가 없거나 거의 없을 것이다. 따라서 softmax보다 둔감하다는 차이점이 있다.

반대로 softmax는 포인트 하나하나마다 정답으로 가려고 하기 때문에 더 민감하다는 차이점이 있다.

Optimization

W값을 찾기 위해 랜덤하게 값을 부여하는 Random search는 매우 좋지 않은 방법이다. 따라서 좋은 W값을 찾기 위해 gradient를 사용한다.

${df(x)\over dx}=\lim_{h\rightarrow0}{f(x+h)-f(x)\over h}$

위와 같은 방식으로 gradient를 계산한다.

그러나 우리의 loss함수는 W에 관한 함수이므로 그저 $\nabla_WL$을 계산하면 된다. 미분을 통해 계산한다. 이 방식은 Analytic gradient라고 한다.

• Numerical gradient: 근사, 느림, 쉽게 작성가능
• Analytic gradient: 정확함, 빠름, error-prone(오류가 발생하기 쉬움)

Gradient Descent

while True:
	weights_grad = evaluate_grad(loss_fn, data, weights)
    weights += - step_size * weights_grad

위와 같이 작성할 수 있다.

Stochastic Gradient Descent (SGD)

전체의 example을 보고 한 step을 가는 것은 비효율적이고 expensive할 수 있다. 따라서 minibatch를 사용하여 근사한다.(32, 64, 128 등)

while True:
	data_batch = sample_training_data(data, 256) # sample 256 examples
    weights_grad = evaluate_gradient(loss_fn, data_batch, weights)
    weights += - step_size * weights_grad