Image features vs ConvNets

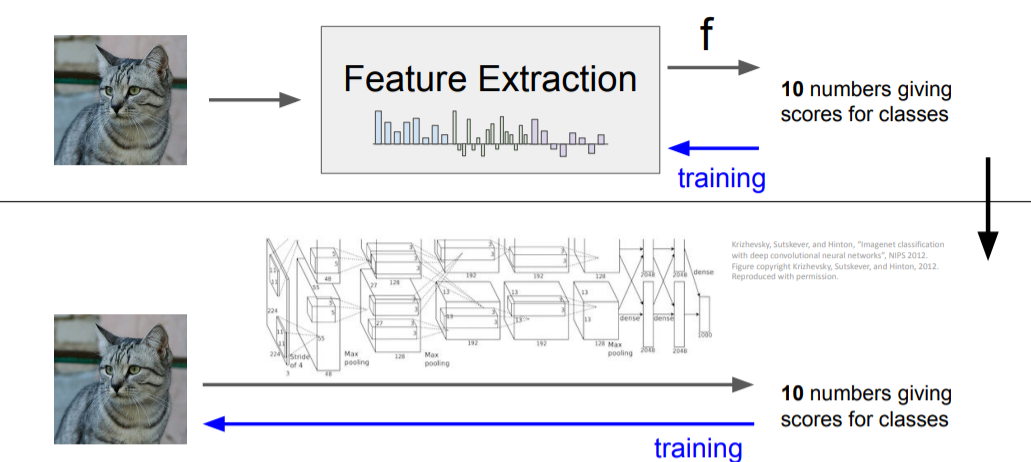
• Feature Extraction : 사람이 직접 color, HoG 등의 feature을 뽑아내 이를 학습시킨다
• ConvNets : 이미지 자체를 학습시킨다.

Computational graphs

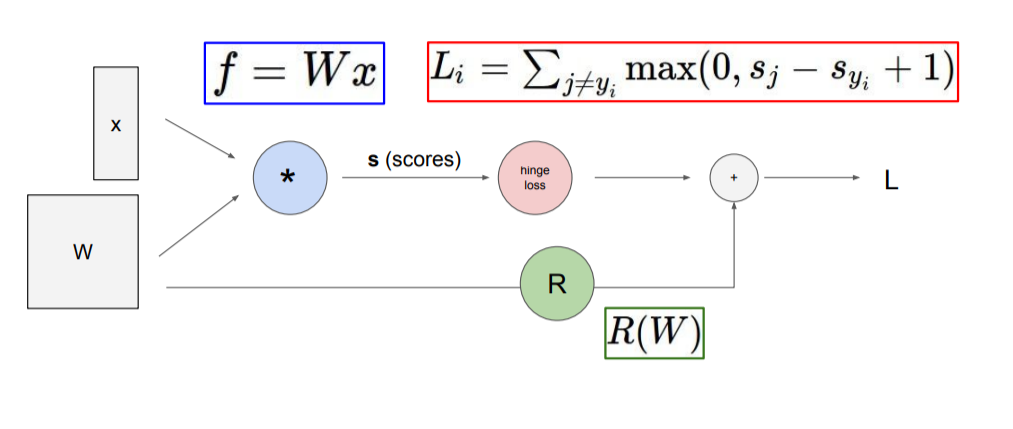위와 같이 그래프를 사용하여 복잡한 구조라도 쉽게 설명될 수 있게 만들 수 있다. 그리고 backpropagation을 계산할 때도 더 간단하게 할 수 있다.

Backpropagation

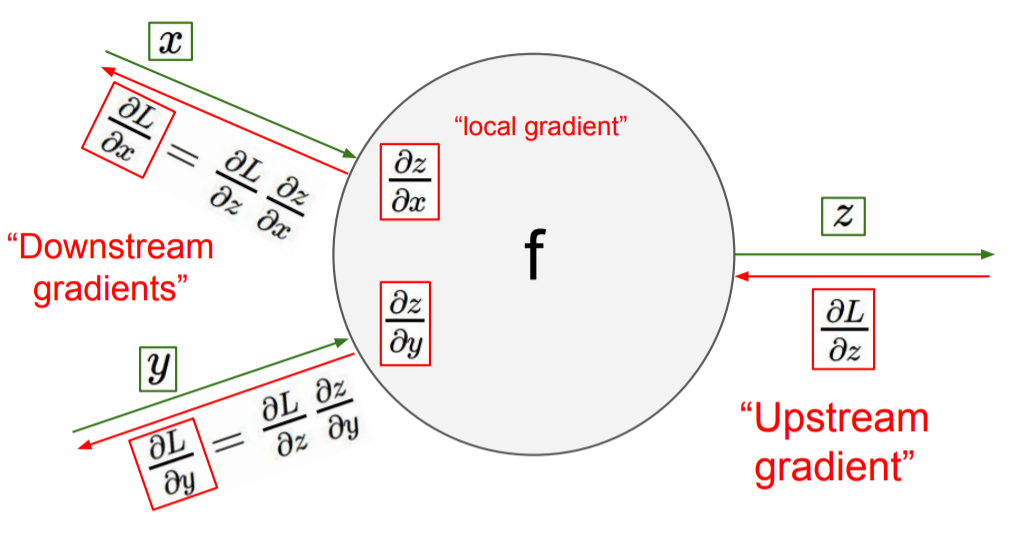f라는 함수(computation)을 하나의 노드로 표현한다. f의 계산 결과값에 대한 backpropagation gradient를 Upstream gradients라고 한다.

위 사진에서는 $z$에 대한 loss $L$의 gradient인 $\partial{L} \over \partial{z}$가 Upstream gradient가 된다.

Chain rule

chain rule을 사용하여 f노드 이전의 값에 대한 gradient를 계산할 수 있다. 위 사진에서 $x$에 대한 gradient는 아래와 같이 계산한다.

이렇게 이전 노드로 전해지는 gradient를 Downstream gradient라고 한다.

Scalar valued function

Backpropagation Example

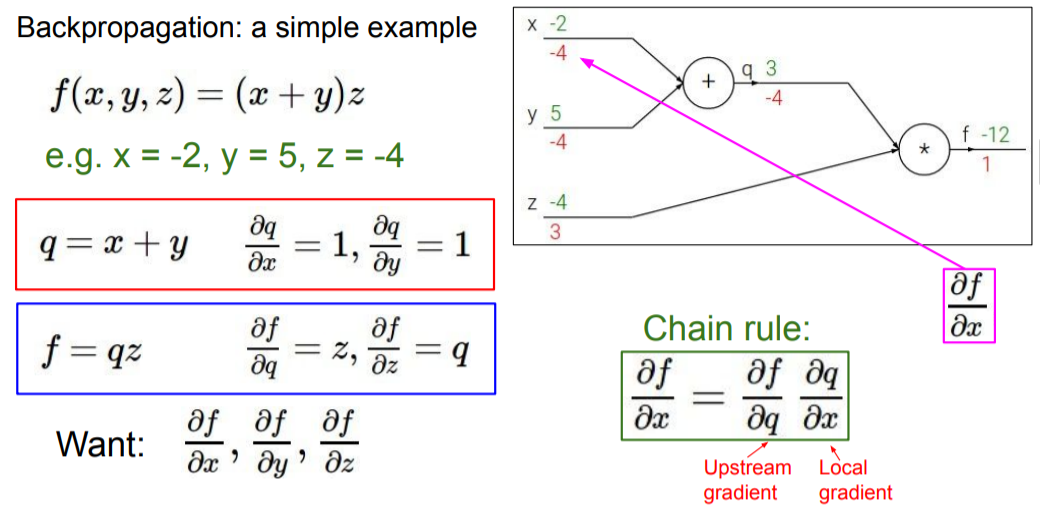$x=-2,\ y=5, \ z=-4$라고 예시가 주어졌다고 하자. 함수 $f$는 옆의 computational graph로 나타낼 수 있다. 각각의 노드의 output은 forward path로 계산이 가능하다.

이제 각각의 값에 대한 gradient를 구하기 위해 backpropagation을 진행한다. chain rule에 의해 아래와 같이 계산된다.

• $f$의 gradient : $\displaystyle{\partial f \over \partial f}=1$

• $q$의 gradient : $\displaystyle{\partial f \over \partial q} = z=-4$

• $z$의 gradient : $\displaystyle{\partial f \over \partial z}=q=3$

• $x$의 gradient : $\displaystyle{\partial f \over \partial q}{\partial q \over \partial x}=-4 \times1=-4$

• $y$의 gradient : $\displaystyle{\partial f \over \partial q}{\partial q \over \partial y}=-4\times1=-4$

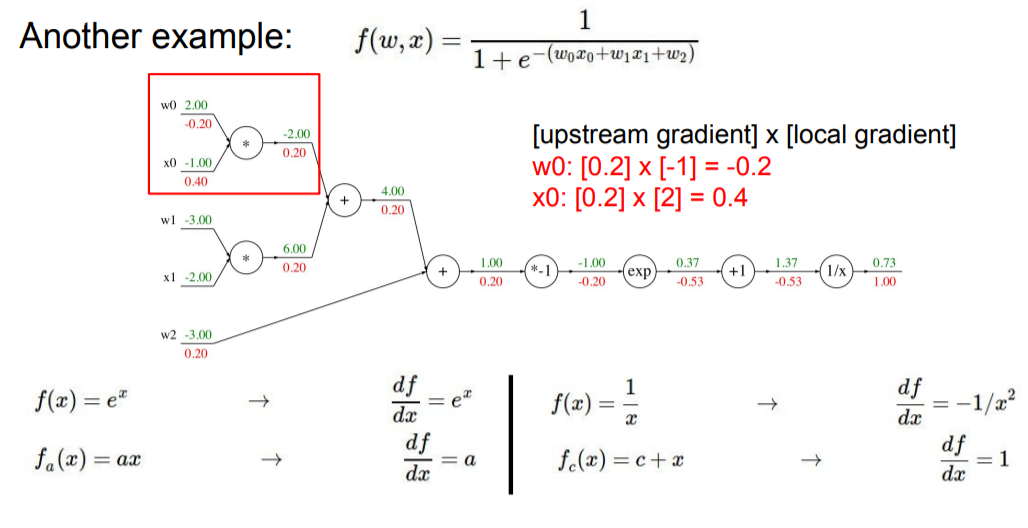다른 예시도 보자.
마지막 노드에 대한 gradient는 1이고, 그 전 노드로 가는 downstream gradient는 아래와 같이 계산할 수 있다.
chain rule에 의해 해당 노드의 gradient는 upstream gradientXlocal gradient가 된다. local gradient는 $\displaystyle{\partial f \over \partial x}=-1/x^2$이므로 upstream gradient인 1에 local gradient값을 곱하면, $\displaystyle 1\times{-1\over 1.37^2}=-0.53$이 된다.

즉, 각 노드의 local gradient를 구해서 chain rule을 활용하여 gradient를 각각 구할 수 있다.

Gradient의 특성

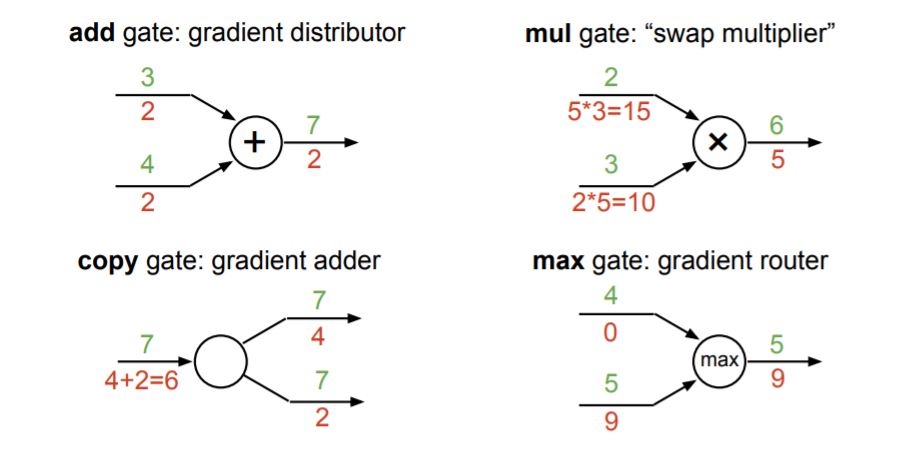
노드에서 시행하는 computation에 따라 gradient의 규칙(특성)이 존재한다. 이를 통해 쉽게 gradient를 계산할 수 있다.

Vector valued functions

vector to vector의 경우에 derivative는 Jacobian이다. 즉, x -> z의 노드에서 $\displaystyle{\partial z \over \partial x}$ 는 jacobian 행렬이 된다.
따지고 보면, $\displaystyle{\partial L \over \partial z}$에서 양수인 element만 남기고 나머지는 0으로 만들면 $\displaystyle {\partial L \over \partial x}$가 된다.

그렇다면 Matrices의 경우에는 어떻게 계산이 될까? 이 때 Jacobian 행렬은 너무 크기가 커져서 실용적이지 못하다. 하지만 간단한 식으로 gradient를 구할 수 있는데 증명과 유도 과정은 너무 복잡해서 이해가 잘 안되었다. 나중에 강의를 다시 보고 이해해 봐야겠다.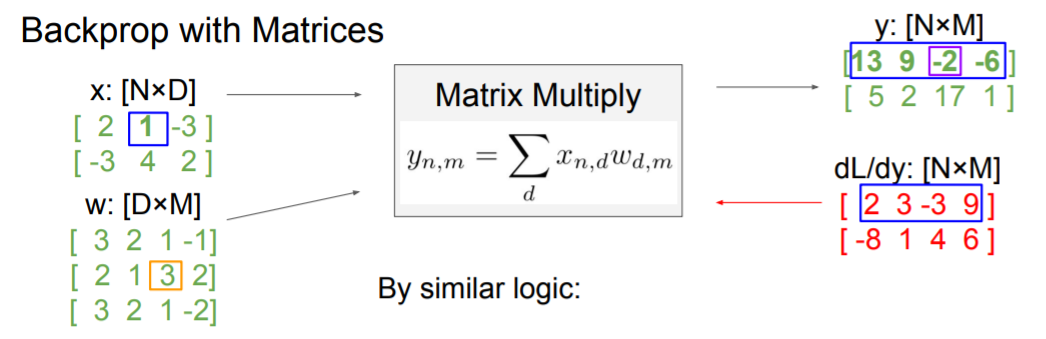위와 같은 식에서 $x,w$의 gradient는

그냥 기존의 값의 차원과 동일하게 맞춰준다 생각하고 계산하면 된다.