Training Neural Networks, Part 1

Activation Functions

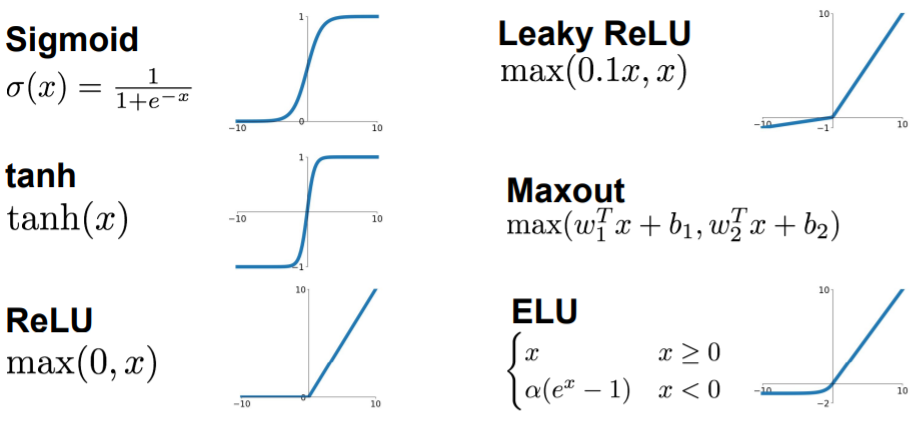
Sigmoid

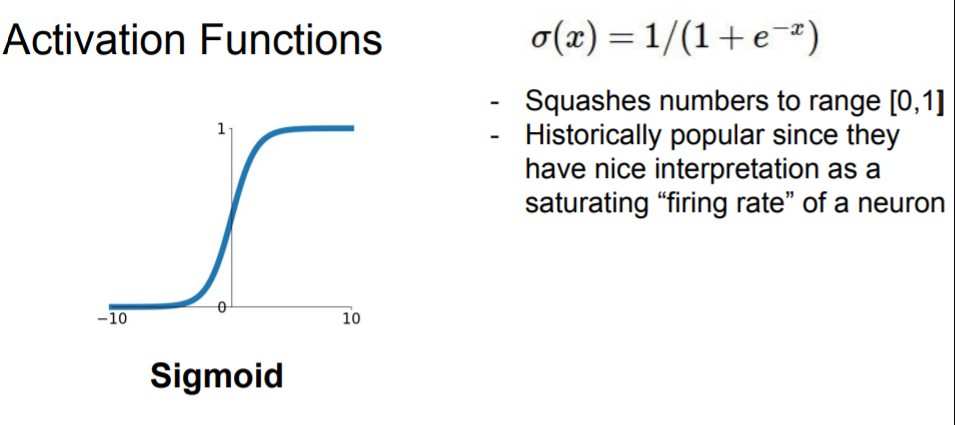0 ~ 1 사이의 값을 갖는다.

문제점

• Saturation이 gradients를 없앤다.

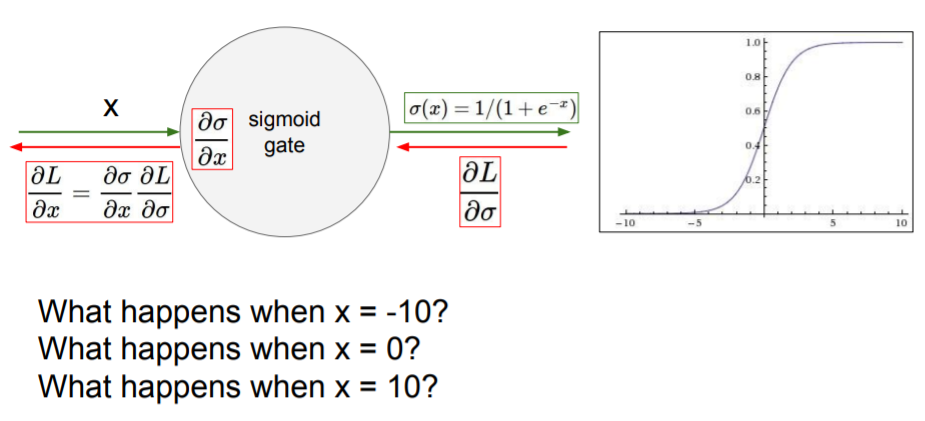  x가 -10이나 10이 되면 gradient는 0이 되어버려 이 값이 backprop된다면 0이 전달되어 gradient가 사라진다.

• Sigmoid outputs are not zero-centered

  만약 input x가 모두 양수라면, w에 대한 gradient는 모두 양수이거나 음수의 방향이다. 즉, 우리가 원하는 방향은 파란색 화살표이지만, 모든 w가 양수의 방향 또는 음수의 방향으로밖에 이동할 수 밖에 없기 때문에 최적의 w를 구하는데 더 오랜 시간이 걸린다.

• exp()로 인해 계산이 비싸진다

tanh

ReLU

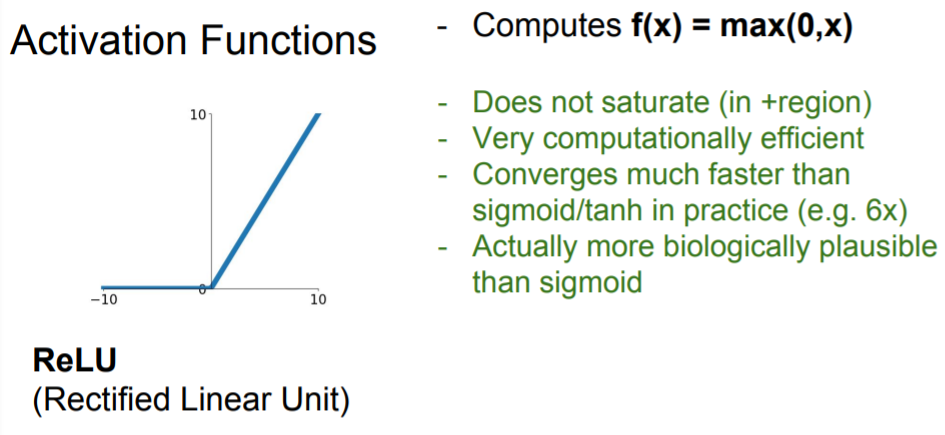
문제점

• Not zero-centered output

• An annoyance

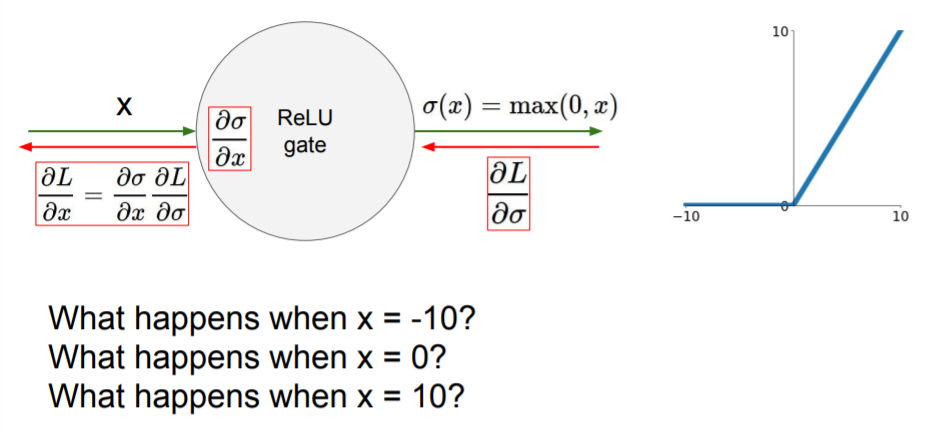  기본적으로 ReLU는 gradient의 절반을 없앤다.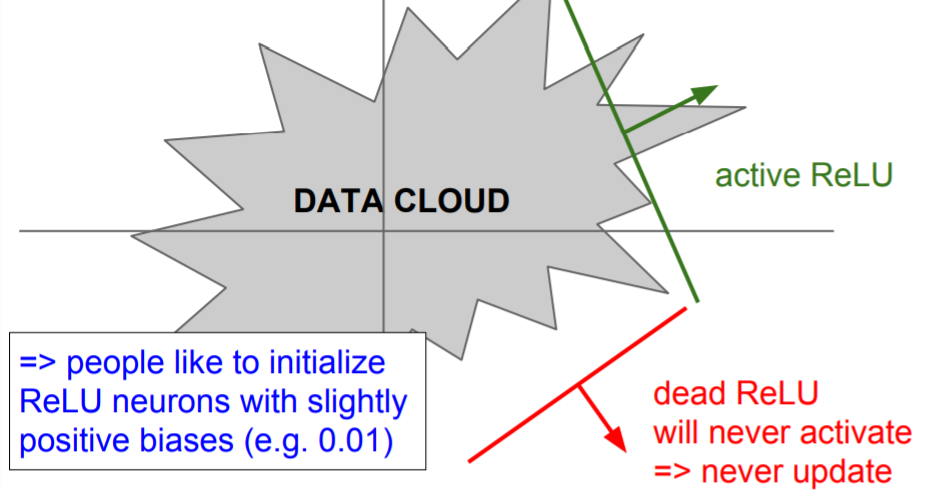DATA CLOUD(training data)에 겹치지 않는 부분에서는 dead ReLU로, 업데이트 되지 않게 된다. 이는 초반 initialize에서 w가 너무 클 때, 또는 초기에는 적절했지만 learning rate가 너무 커서 w값이 날 뛸 때 주로 일어난다. 잘 학습시키더라도 기본적으로 10%~20%의 gradient는 죽게된다고한다.
  
  이를 해결하기 위해 ReLU를 초기화할 때 positive biases를 추가해 주는 경우가 있다. 업데이트 시에 active ReLU가 될 가능성을 조금이라도 더 높여주기 위함이다. 대부분은 zero-biases로 초기화한다.

Leaky ReLU

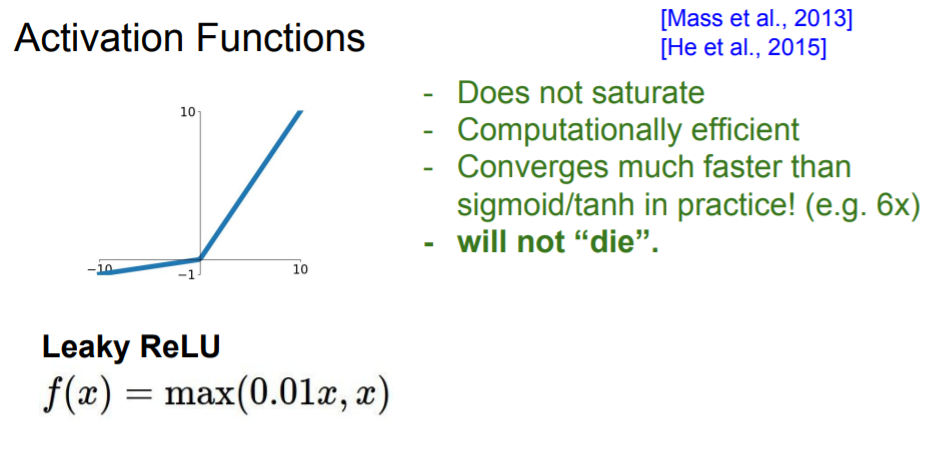
PReLU

기울기가 $\alpha$로, backprop하면서 학습되는 파라미터이다.

ELU

Maxout "Neuron"

ReLU와 LeakyReLU의 좀 더 일반화된 형태로, saturation이 되지 는다 그러나 뉴런당 파라미터가 $w_1, w_2$로 두배가 된다.

보통 ReLU를 사용한다.

Data Preprocessing

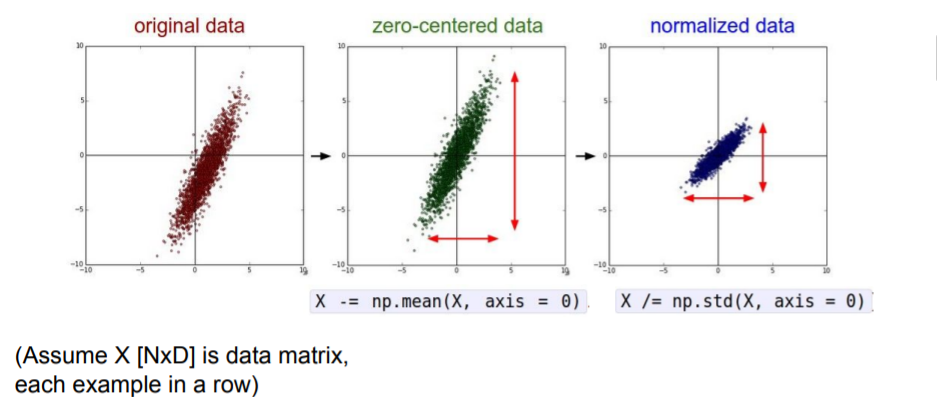
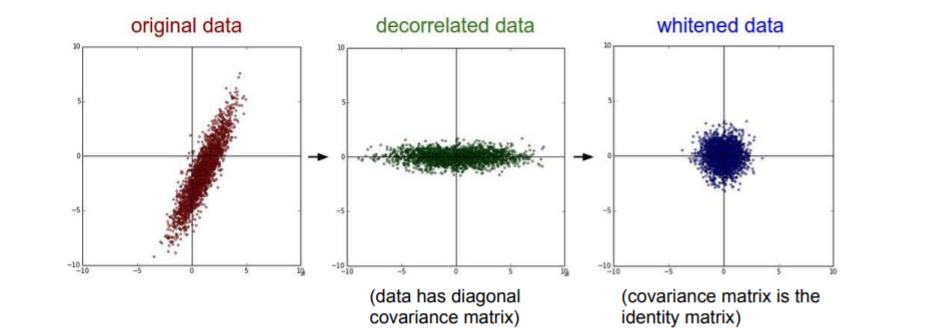
PCA나 Whitening의 방식도 있지만 이미지에서는 굳이 낮은차원으로 projection시키지는 않는다. 그리고 Normalize도 굳이 할 필요 없다. 이미지를 다룰때는 zero-mean을 보통 사용한다.

Weight Initialization

What happpens when $w=0$ init is used?

모든 뉴런이 같은 일을 한다. 모든 뉴런이 죽어 업데이트가 되지 않는 것은 아니다. 가중치가 0이므로 모든 뉴런은 모두 다 같은 연산을 수행한다. 출력도 같고, gradient도 서로 같을 것이다.

1. 가중치 편차 0.01 Small random numbers로 초기화

$\mu=0, \sigma=0.01$ 인 gaussian

W = 0.01 * np.random.randn(D, H)

작은 네트워크라면 symmetry breaking에 충분하지만 deeper 네트워크에서는 문제가 생긴다.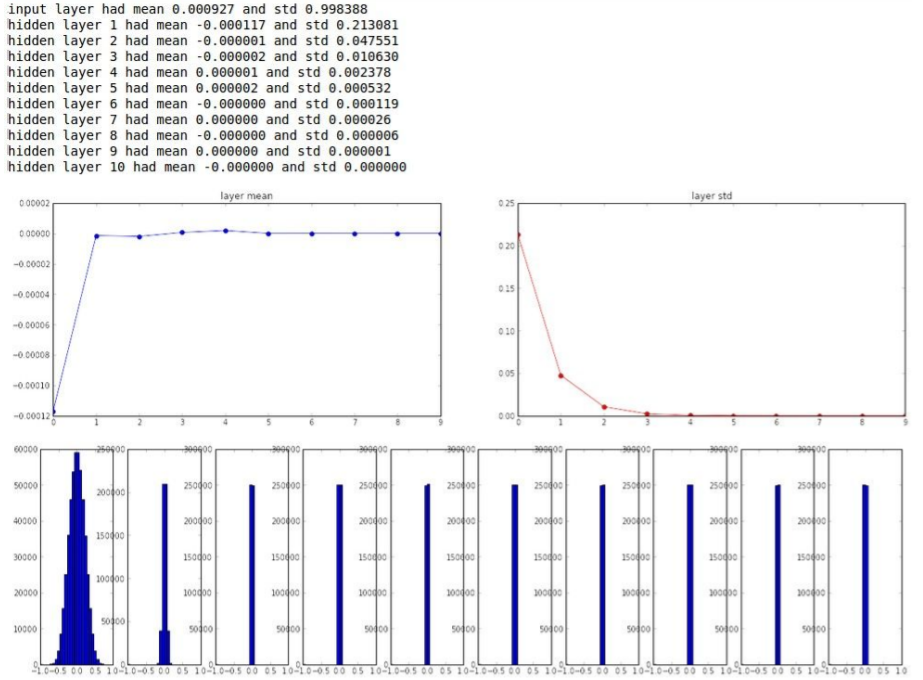deep network에서 초반에는 가우시안 분포가 잘 나타나지만, $w$가 너무 작은 값들이라서 $w$를 곱할수록 출력 값이 급격히 줄어 std가 0이 되어버린다. 즉 모든 activation이 0이 된다.

2. 가중치 편차 1

W = np.random.randn(fan_in, fan_out) * 1.0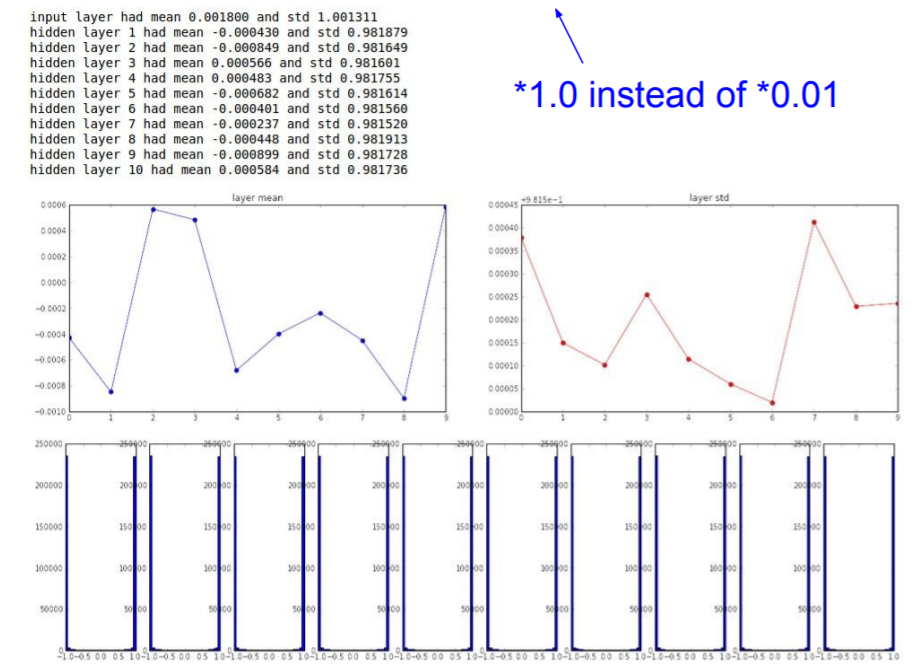

가중치가 큰 값을 가지므로, tanh의 출력은 saturate된다. 따라서 출력이 항상 1이거나 -1이 된다. 따라서 gradient는 모두 0이 되어 업데이트가 되지 않을 것이다. (Almost all neurons completely saturated, either -1 and 1. Gradients will be all zero)

3. Xabier initialization

W = np.random.randn(fan_in, fan_out) / np.sqrt(fan_in)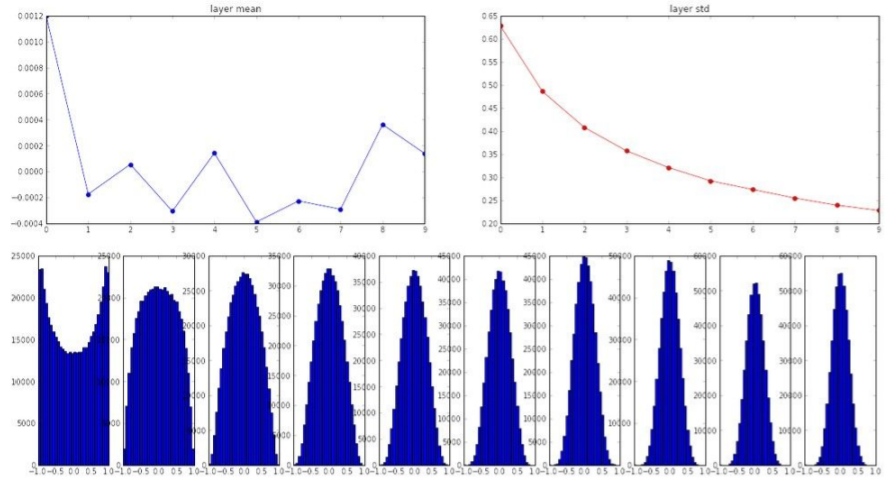

standard gaussian으로 뽑은 값을 입력의 수로 스케일링해주어 기본적으로 입/출력의 분산을 맞춰준다. 입력의 수가 많은 경우에는 작은 가중치, 입력의 수가 적은 경우에는 그 반대가 된다.

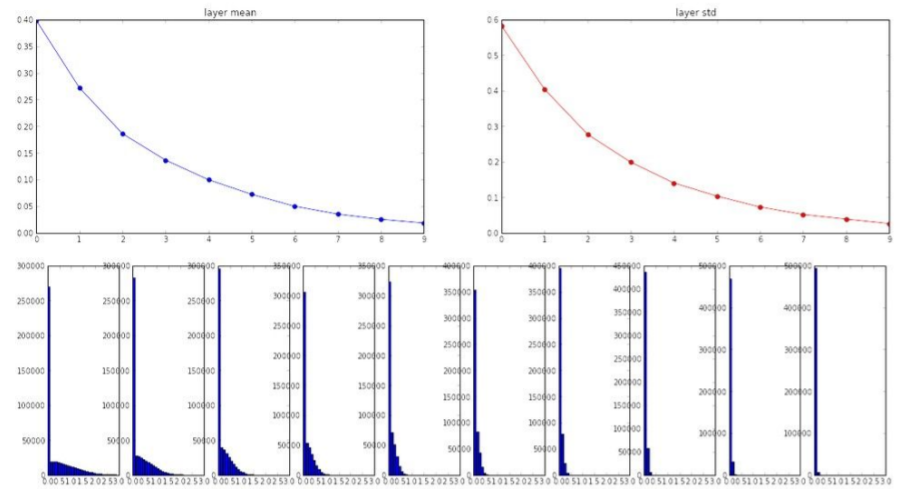그러나 linear activation이 아니라 ReLU를 사용하면 출력의 절반이 0이 되어 출력의 분산을 반토막 낸다. 이때문에 값이 너무 작아진다.

이를 해결하기 위해

W = np.random.randn(fan_in, fan_out) / np.sqrt(fan_in / 2)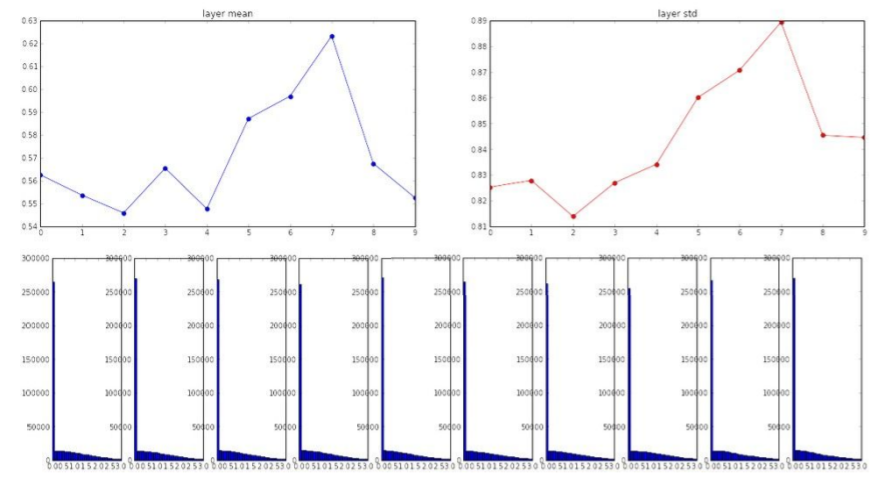

를 사용하여 좋은 결과를 내었다.

Batch Normalization

가중치를 잘 초기화하는 대신에 이 과정을 통해 모든 레이어가 Unit Gaussian이 되도록 한다.
N x D(차원) 에서 각 D(차원)마다의 평균과 분산을 계산하여 Normalize하는 방식으로 진행된다. 보통 FC-layer이나 Conv-layer 이후, 그리고 nonlinearity 이전에 사용된다.

CNN에서는 공간적인 구조를 학습하기를 원하기 때문에 activation map 하나당 하나의 평균과 분산을 갖도록 BN을 적용한다.

$\displaystyle \hat x^{(k)}={x^{(k)}-\text E[x^{(k)}] \over \sqrt{\text{Var} [x^{(k)}]}}$

으로 Normalize를 하고, 다시 이 값을 BN전의 값으로 되돌리기 위해 아래와 같은 식을 사용한다. $\gamma$는 스케일링, $\beta$는 이동을 담당한다.

$\displaystyle y^{(k)}=\gamma^{(k)}\hat x^{(k)}+\beta^{(k)}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(\begin{aligned} \gamma^{(k)} &= \sqrt{\text{Var}[x^{(k)}]} \\ \beta^{(k)}&=\text E[x^{(k)}] \end{aligned}\right)$

Batch Normalization을 쓰면,

• gradient의 흐름을 원활하게 해주어 더 학습이 잘됨
• learning rates를 더 키울 수 있음
• regularization의 역할도 함

Test time에서의 BN

test time에서는 또 다시 mean / std를 계산하지 않고 training time에 running averages등으로 계산한 값을 사용한다.

https://eehoeskrap.tistory.com/430 $\leftarrow$ 여기에 자세히 설명되어있다.

Babysitting the Learning Process

1. Preprocess the data

2. Choose the architecture

   • gradient가 제대로 흐르고, loss가 합리적인지 확인하기 위해 sanity check를 해본다.
   • 적은 데이터와 작은 regularization을 가지고 learning rate를 찾는다. 좋은 learning rate를 찾는 것이 가장 우선이다. 만약 loss가 너무 줄지 않는다면 learning rate가 너무 작기 때문이므로 키워주는 식으로 조절한다. 보통 [1e-3, 1e-5] 사이의 값으로 설정된다

Hyperparameter Optimization