Training Neural Networks, Part2

참고자료
https://cs231n.github.io/neural-networks-2/

Last Time

Activation Functions

보통의 네트워크에서는 ReLU가 가장 좋은 선택이다

Weight Initialization

네트워크가 깊어질수록 가중치 초기화는 중요하며, 너무 작으면 gradient가 0이되어 학습이 안되고, 너무 크면 tanh같은 경우 saturate된다.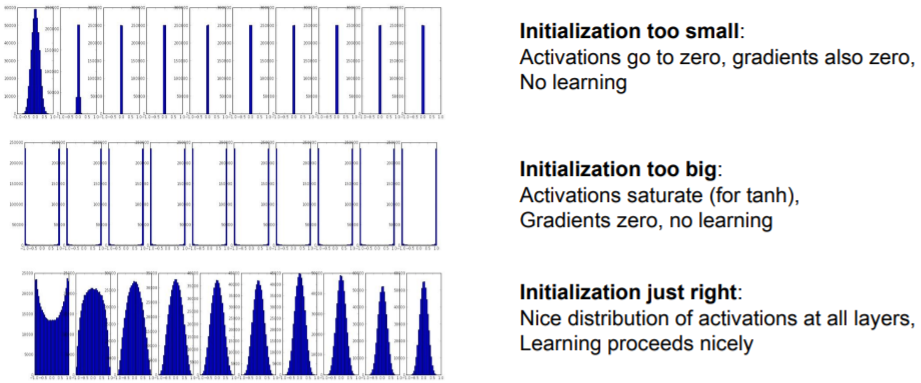

Data Processing

CNN은 zero-mean을 주로 사용한다.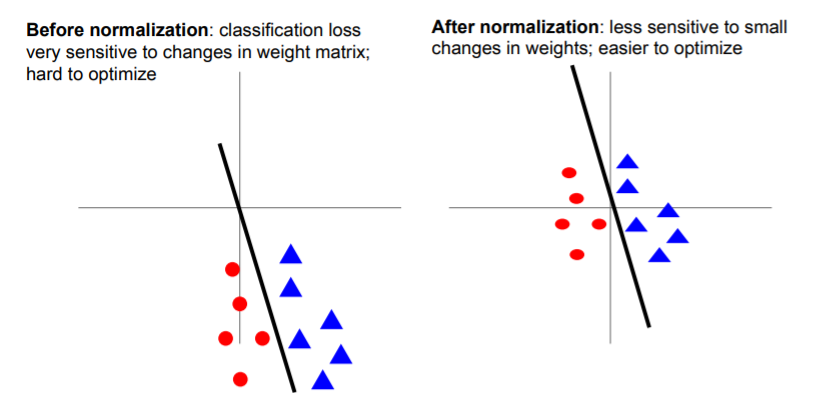binary classification에서 왼쪽 경우처럼 normalization이 되지 않으면 기울기가 조금만 변해도 매우 큰 변화가 일어나지만 오른쪽과 같은 경우에는 weight의 변화에 덜 민감해져서 최적화가 쉽다.

Hyperparameter Search

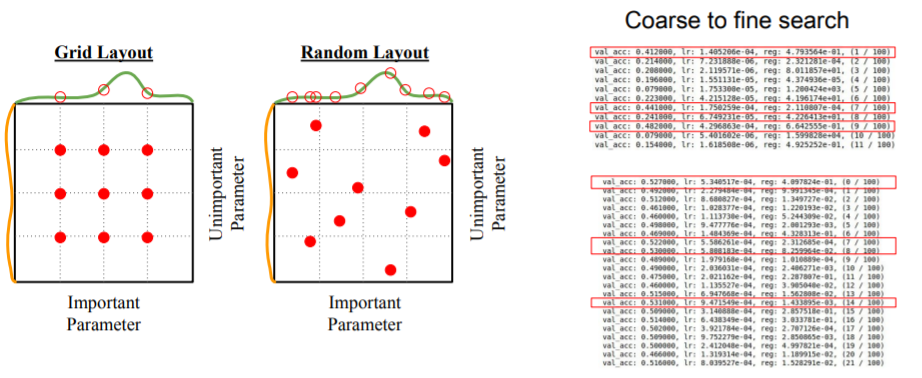
Random Search가 주로 더 좋으며, 먼저 Coarse search를 통해 최대한 넓은 범위에서 적은 iteration으로 찾고, 좋은 범위에서 다시 fine search를 통해 적절한 hyperparameter을 찾는다.

1. Fancier optimization

1) SGD의 문제

차원에 따라 업데이트 속도가 다른경우

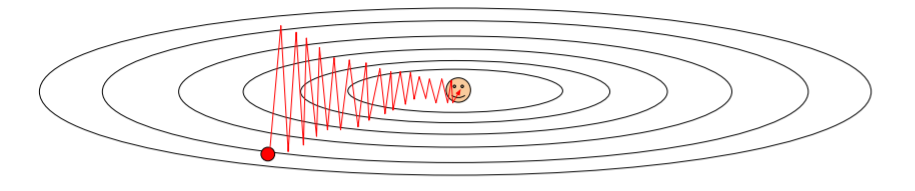위와 같은 상황에서는 수평방향보다 수직방향에서 가중치 업데이트에 훨씬 더 민감하다. 따라서 수평방향은 매우 천천히 업데이트되고 수직방향은 매우 빠르게 지그재그로 업데이트 된다.

Very slow progress along shallow dimension, jitter along steep direction

매우 많은 차원에서 위와 같은 상황이 빈번히 발생하며, 이는 큰 문제가 된다.

local minima & saddle point

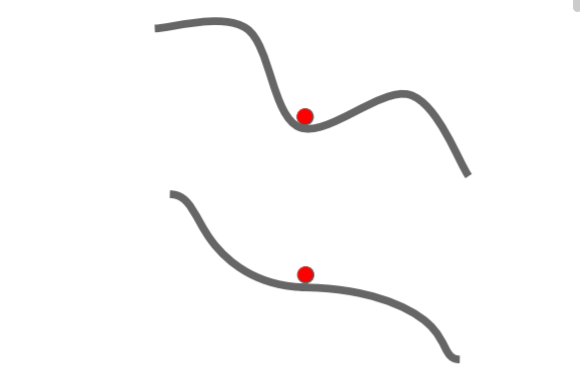첫번째처럼 local minima에서 gradient가 0이 되어 갇히거나, 두번째처럼 saddle point에서 gradient가 0이되어 멈출 수 있다. 고차원에서는 saddle point가 더 빈번하게 나타난다.

미니배치에서의 문제

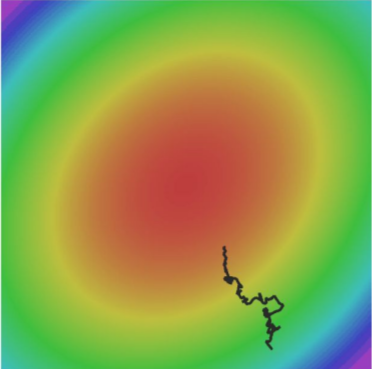미니배치에 따라 노이즈가 추가될 수 있어 정확한 방향을 찾지 못하고 돌아다니다가 매우 긴 시간에 최적화 될 수 있다.

2) SGD + Momentum

rho는 주로 0.9 또는 0.99 로 주어지는 hyperparameter

gradient 방향만 보는 것이 아니라, velocity(속도)까지 보면서 최적화를 진행한다. 이를 통해 진행되는 방향에 관성을 줄 수 있다. 즉, local minima이거나 saddle points에서 gradient=0이 되어도 계속 진행할 수 있다.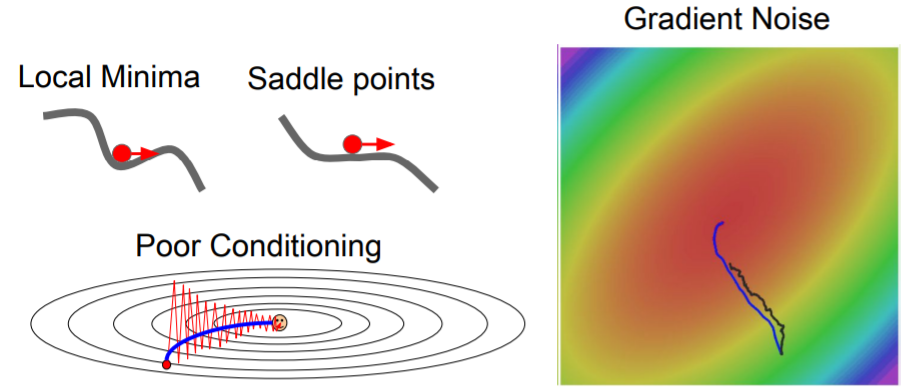

vx = 0
while True:
	dx = compute_gradient(x)
    vx = rho * vx + dx
    x += learning_rate * vx

3) Nestoerov Momentum

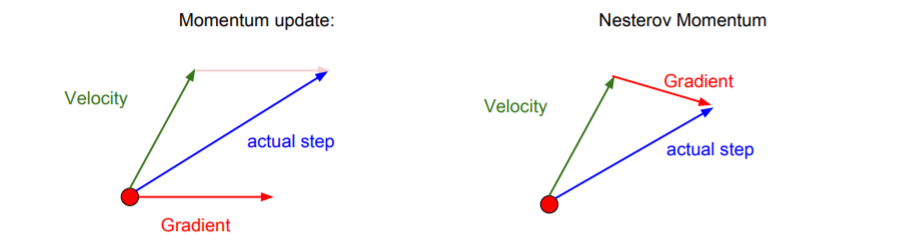기존 Momentum 업데이트 방식은 현재 지점에서 gradient를 계산한 뒤에 velocity와 섞어준다. Nesterov Momentum은 현재 지점에서 우선 velocity방향으로 움직이고, 그 지점에서의 gradient를 계산한다. 그리고 다시 원점으로 돌아가서 둘을 합친다. 이는 velocity의 방향이 잘못되었을 경우에 현재 gradient의 방향을 좀 더 활용할 수 있게 해준다.

Nesterov Momentum

$\begin{aligned} v_{t+1} &= \rho v_t-\alpha\nabla f(x_t+\rho v_t)\\ x_{t+1} &= x_t + v_{t+1} \end{aligned}$

변수들을 적절히 변형해주면 한 점에서 loss와 gradient를 모두 계산하여 계산의 복잡함을 해결할 수 있다. $\tilde x_t = x_t + \rho v_t$ 로 놓고,

$\begin{aligned} v_{t+1} &= \rho v_t - \alpha \nabla f(\tilde x_t) \\ \tilde x_{t+1} &= \tilde x_t - \rho v_t + (1+\rho)v_{t+1}\\ &= \tilde x_t + v_{t+1} + \rho(v_{t+1} - v_t) \end{aligned}$

dx = compute_gradient(x)
old_v = v
v = rho * v - learning_rate * dx
x += -rho * old_v + (1 + rho) * v

Momentum

$\begin{aligned} v_{t+1} &= \rho v_t + \nabla f(x_t)\\ x_{t+1} &= x_t - \alpha v_{t+1} \end{aligned}$

4) AdaGrad

훈련 도중 계산되는 gradients를 활용한다. velocity 대신에 grad squared를 사용한다.

grad_squared = 0
while True:
	dx = compute_gradient(x)
    grad_squared += dx * dx
    dx -= learning_rate * dx / (np.sqrt(grad_squared) + 1e-7)

5) RMSProp

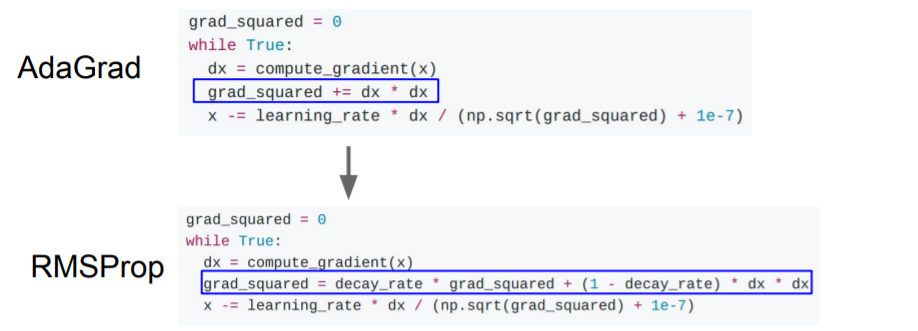AdaGrad는 오랜 시간이 지날수록 계속해서 gradient의 제곱으로 나누어주기 때문에 점점 step size가 줄어들어 매우 천천히 진행된다. 만약 convex case가 아니라 saddle point같은 경우에는 멈춰버릴 수 있다. 따라서 grad_squared 부분을 변형하여 RMSProp의 방식이 등장하였다.RMSProp은 AdaGrad와 같이 과거의 기울기들을 똑같이 더해가는 것이 아니라 먼 과거의 기울기는 조금 반영하고 최신의 기울기를 많이 반영한다.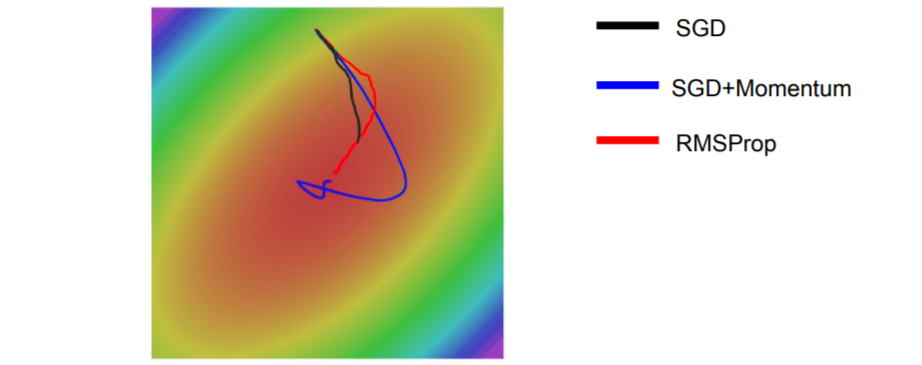

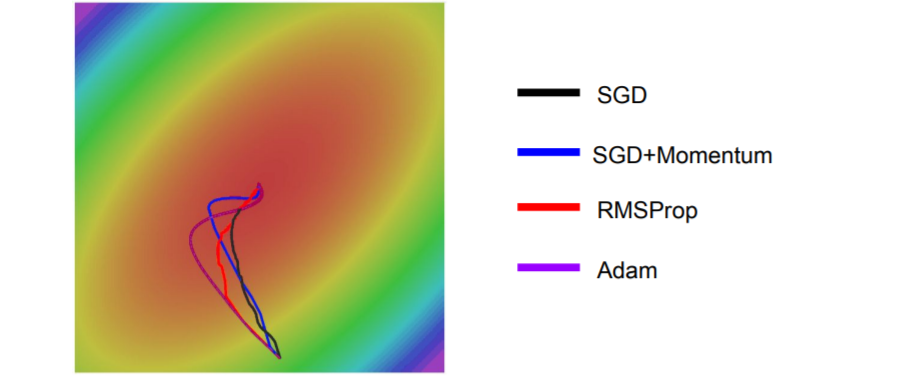
6) Adam

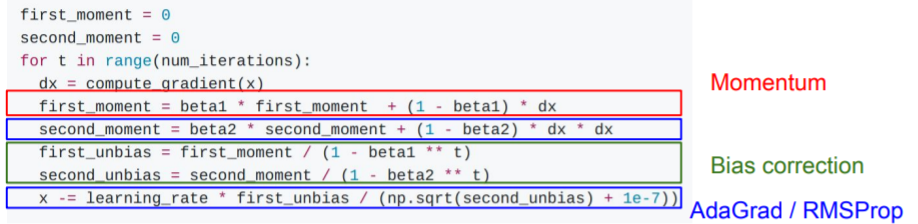Adam은 Momentum + RMSProp 과 비슷하다. 그러나 beta2는 0.9 또는 0.99로 1에 가까운 값인데, second_moment=0 으로 초기화하고 시작하기 때문에 초기에 second_moment는 1회 업데이트 이후에도 여전히 0에 가깝다. update시에 second_moment로 나누게 되는데, second_moment가 0에 가까우므로 초기 step이 매우 커지게 된다. 초기에 가파라서 발생하는 것이 아니라 문제가 생긴 것이므로 Bias correction을 통해 이를 해결해야한다.

일반적으로 Adam + beta1=0.9, beta2=0.999로 하고, learning rate=1e-3 or 5e-4로 진행하면 거의 모든 모델에서 잘 동작한다.

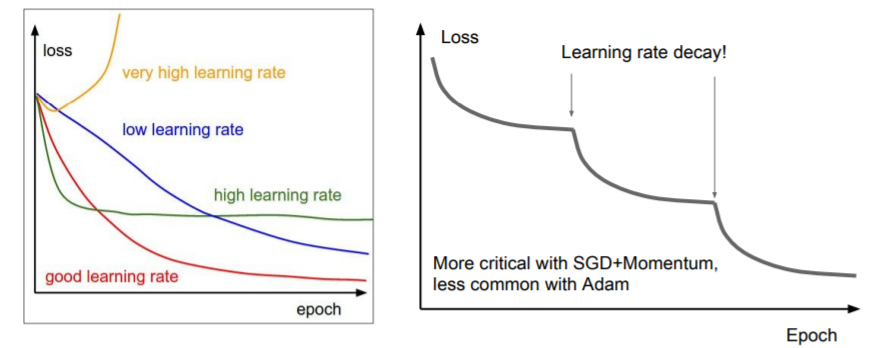
7) Learning rate의 결정

학습을 진행하면서 좋은 learning rate를 지속해서 가져가기 위해 learning rate decay를 사용하기도 한다.

• step decay
  every few epochs마다 learning rate를 줄여나간다.

• exponential decay
  $\alpha = \alpha_0 e^{-kt}$

• 1/t decay
  $\alpha = \alpha_0 / (1+kt)$

• 또는 loss의 감소가 줄어들 때나 일정 100000iter마다 learning rate decay를 진행할 수도 있다.

8) Second-Order Optimization

First-Order Optimization

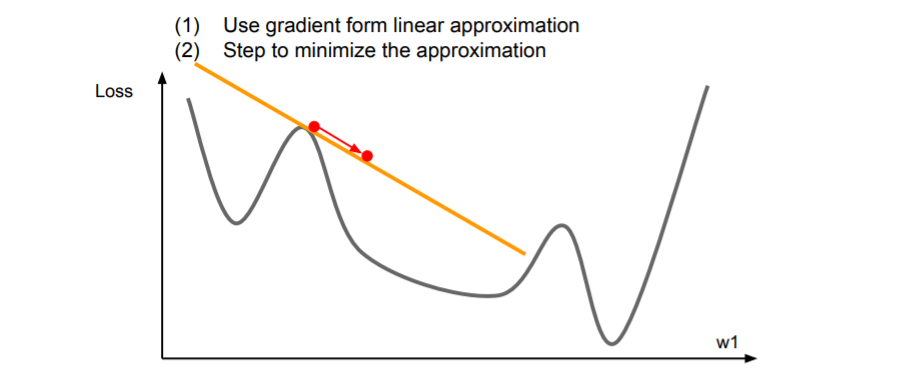우리는 1차 미분을 통해 다음 step을 계산해왔다. 그러나 이는 충분히 빠르지 못하다.

Second-Order Optimization

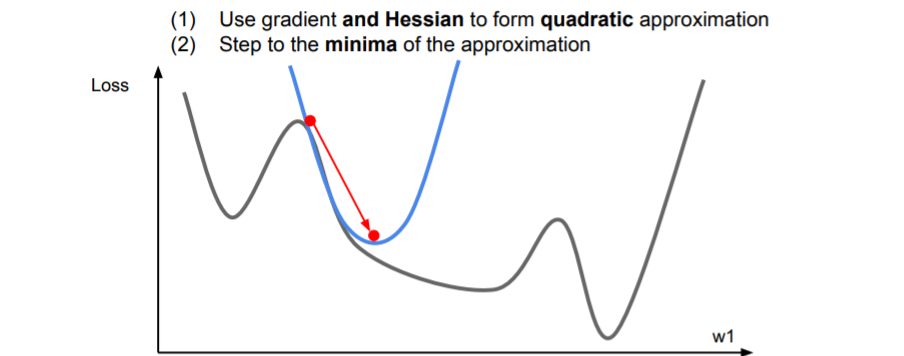2차 근사를 사용하여 2차 테일러 근사함수가 되면 minima에 더 잘 근접할 수 있다. 이를 다차원으로 확장시켜보면 Newton step이라고 한다.2차 미분값들로 된 행렬인 Hessian matrix를 계산하고, 이의 역행렬을 이용하면 실제 손실함수의 2차 근사를 이용해 minima로 곧장 이동할 수 있다.

이 방식은 learning rate 가 없다. 2차 근사 함수의 minima로 이동하기 때문이다. 매 step마다 minima로 이동한다.

그러나 실제로는 learning rate가 필요하다. (2차 근사도 완벽하지 않기 때문이다) 그러나 deep learning에서는 사용할 수 없다. Hessian matrix는 NxN 매트릭스로 매우 큰 메모리가 필요하기 때문이다. 따라서 실제로는 quasi-Newton methods를 사용한다.

그러나 ! 실제로는 Adam을 가장 많이 사용한다.
가금 style transfer와 같이 stochasticity와 파라미터가 적은 경우에서 최적화를 할 때 L-BFGS를 사용하기도 한다.

9) Model Ensembles

머신러닝에서 주로 사용되는 방식인데, 독립적인 여러 모델을 학습시키고, test time에서 이들 결과의 평균을 사용한다. 이를 통해 약 2%의 성능향상을 기대할 수 있다. 이를 통해 validation set과 training set의 갭을 줄이고 robust한 결과를 낼 수 있도록 한다.

한 모델을 training시키면서 중간중간의 결과들(snapshots of a single model during training)을 앙상블할 수도 있다. 또는 한 모델을 training할 때 learning rate를 크게 했다 작게 했다 하면서 loss fn의 여러 구간을 모두 확인하여 이를 앙상블 할 수도 있다.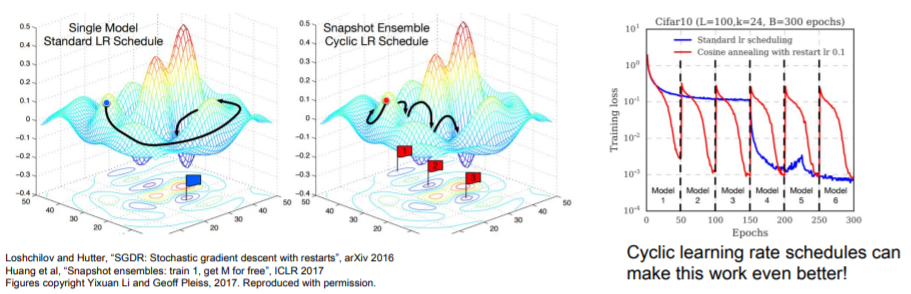 학습하는 동안 파라미터의 exponentially decaying average를 계속 계산하는 polyak averaging이라는 방법도 있는데 이 방식은 잘 이해가 안됐다.

How to improve single-model performance?

모델이 training data에 과적합되는 것을 막기 위해 regularization을 사용한다.

2. Regularization

1) Add term to loss

L2 regularization 등과 같은 term을 loss fn에 추가한다.

2) Dropout

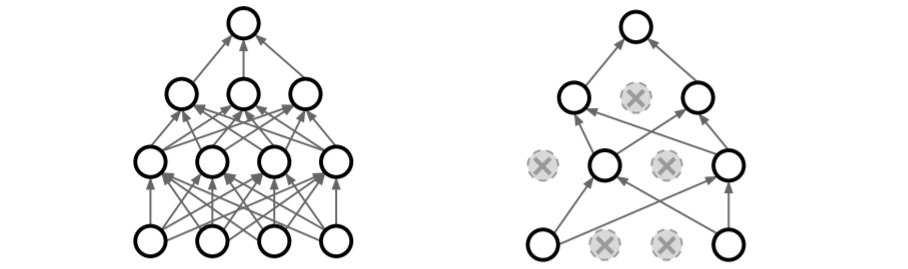forward pass시에 일부 뉴런의 activation 값을 0으로 만드는 방식이다. 각 layer마다 이를 수행하여 진행하고 보통 fc layer에서 사용한다. conv net에서는 일부 channel을 dropout하기도 한다. dropout하는 뉴런은 매 iter마다 달라진다.

p = 0.5 # 뉴런의 active 확률이고, higher = less dropout

def train_step(X):
	""" X contains the data """
    
    # 3 layer neural network에서의 forward pass 예시이다.
    H1 = np.maximum(0, np.dot(W1, X) + b1)
    U1 = np.random.rand(*H1.shape) < p # 첫번째 dropout mask
    # *H1.shape은 H1.shape의 튜플인 (2,3)을 unpacking한다.
    # 즉 same as np.random.rand(2,3)
    H1 *= U1 # drop!
    H2 = np.maximum(0, np.dot(W2, H1) + b2)
    U2 = np.random.rand(*H2.shape) < p # 두번째 dropout mask
    H2 *= U2 # drop!
    out = np.dot(W3, H2) + b3

Dropout이 왜 좋은가?

feature들 간의 상호작용을 방지한다.

만약 고양이를 분류하는 네트워크가 있을 때, 어떤 뉴런은 눈, 어떤 뉴런은 꼬리 등을 결정하는 뉴런이라고 하자. 네트워크는 이들을 취합해서 결정한다. 만약 dropout을 적용한다면 일부 feature에 크게 의존하지 못하게 하여 overfitting을 막을 수 있다.

또한, Dropout을 새로운 관점으로 보는 방식이 등장하였는데, dropout을 한 여러 종류의 모델들을 앙상블한다는 것이다. 매 iter마다 dropout된 새로운 모델이 생기고 이들을 앙상블한다는 것이다. 그리고 이들은 파라미터를 공유한다.

Test time에서 dropout

droput을 사용하게 되면

이 된다. 그러나 test time에도 train과정처럼 randomness를 줄 수는 없다. 따라서 randomness를 averge out시키고 싶고 이는 적분을 통해 randomness를 marginalize out시키는 것으로 생각할 수 있다. 즉,

그러나 이 적분식은 매우 어렵다. 이를 근사하기 위해 확률을 사용한다.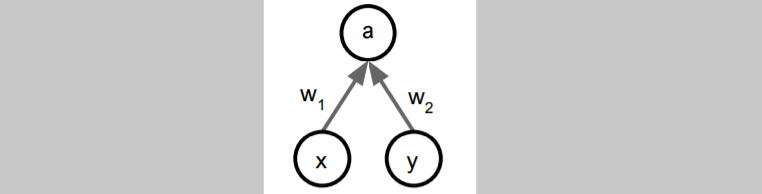위와 같은 single neuron의 상황을 가정해보자.

• Test time : $E[a]=w_1x + w_2y$
• Training time : $\displaystyle E[a]={1\over4}(w_1x + w_2y)+{1\over4}(w_1x + 0y)+{1\over4}(0x + 0y)+{1\over4}(0x + w_2y)={1\over2}(w_1x+w_2y)$

으로, training time에서의 기댓값은 test time의 절반이 된다.

따라서 test time시 dropout probability를 곱하여 계산하기만 하면 간단하게 적분을 근사할 수 있다.

def predict(X):
  # ensembled forward pass
  H1 = np.maximum(0, np.dot(W1, X) + b1) * p # NOTE: scale the activations
  H2 = np.maximum(0, np.dot(W2, H1) + b2) * p # NOTE: scale the activations
  out = np.dot(W3, H2) + b3

test시간에 곱하기를 사용하는 것이 부담스러울 수 있으므로 역으로 training time에서 미리 p로 나누어서 진행할 수도 있다.

Batch Normalization의 역할과 비슷하기도 하다.

BN은 mini batch로 하나의 데이터가 샘플링 될 때 매번 서로 다른 데이터들과 만나게 된다. Train time에는 각 데이터에 대해서 얼마나 어떻게 정규화할지에 대한 stochasticity(임의성)이 존재했다. 하지만 test time에는 정규화를 mini batch단위가 아니라 global 단위로 수행함으로써 임의성을 평균화시킨다. 이런 특성은 dropout과 유사한 regularization효과를 준다.

실제로 BN을 사용할 때는 dropout을 사용하지 않는다.

2) Data Augmentation

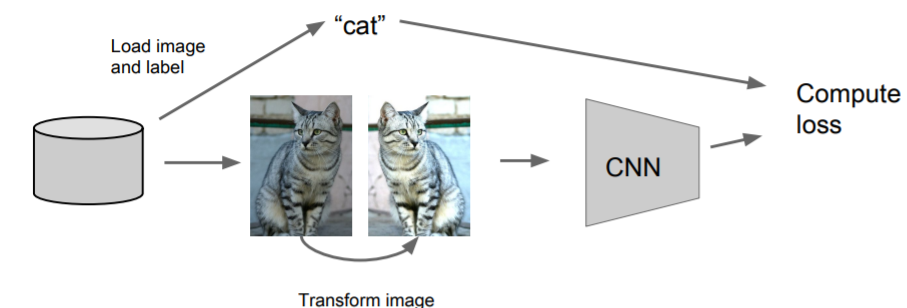이미지를 뒤집거나, 임의로 자르거나 해도 같은 이미지라는 것을 사용한다.이미지의 contrast나 brightness를 변형하기도 한다. 그러나 이는 자주 사용하지 않는다.

data augmentation의 여러 방법들

• translation
• rotation
• stretching
• shearing
• lens distortions ...

3) DropConnect

activation이 아닌 weight matrix를 임의적으로 0으로 만들어주는 방법이다. dropout과 동작은 비슷하다.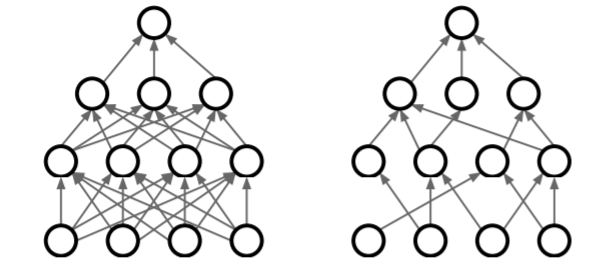

4) Fractional Max Pooling

위와 같이 Pooling연산을 수행할 지역이 임의로 선정되고, test time에는 pooling regions를 고정시키거나 여러 pooling regions를 average over시킨다. 많이 사용하지는 않지만 좋은 아이디어라고 한다.

5) Stochastic Depth

train time에 일부 layer을 랜덤하게 drop한다. test time에는 전체 네트워크를 사용한다.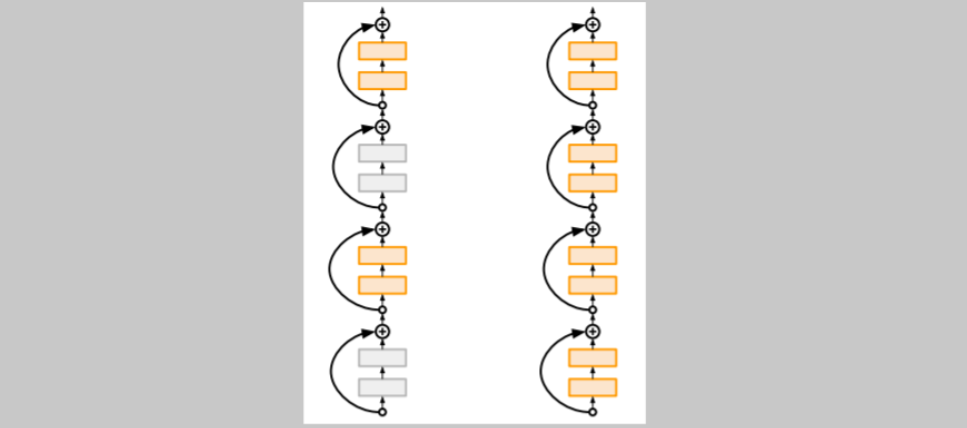

보통 Batch Normalization으로 충분하지만 그럼에도 과적합이 발생하면 dropout등의 방식을 추가한다.

3. Transfer Learning

데이터가 지나치게 작으면 과적합이 발생할 수 있다. 그래서 다른 커다란 데이터셋으로 학습시킨 features를 사용하여 작은 데이터셋에 적용할 수 있다.1. 먼저 Imagenet과 같은 큰 데이터셋으로 학습시킨다.

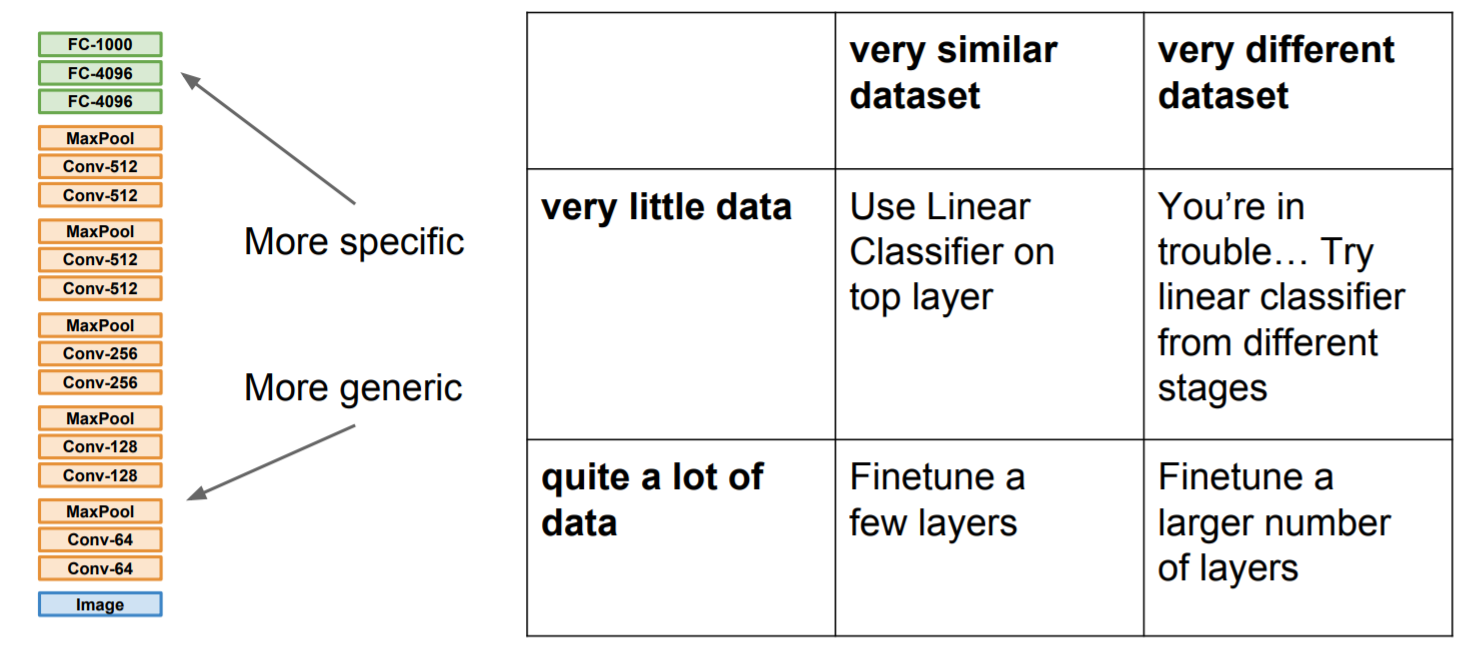
2. 작은 데이터셋과 작은 클래스(C)가 존재할 때 1번에서 진행한 features를 그대로 들고와서 마지막 fc layer만 조정하고(4096 -> C) 이 fc layer만 학습시킨다.

3. 만약 조금 더 큰 데이터셋을 갖고 있다고 하면 네트워크를 fine tuning할 수 있다. 데이터가 더 많이 있다면 더 많은 layers를 추가로 학습시킬 수 있다.

trasfer learning하려는 모델의 데이터셋과 현재 사용하는 데이터셋이 비슷하다면 크게 문제될 것은 없지만 만약 다르다면 창의적인 방법이 필요할 수 있다. 아래 그림은 데이터 셋의 상황에 따른 행동이다.