[EECS 498-007 / 598-005] 강의정리 - 12강(CS231n 10강) Recurrent Neural Networks

ONground·2022년 4월 17일

EECS 498-007 / 598-005

[CS231n] + [EECS 498-007 / 598-005]

목록 보기

9/17

Recurrent Neural Networks

Process Sequences
1.1) Sequential Processing of Non-Sequential Data
Recurrent Neural Networks
2.1) (Vanilla) Recurrent Neural Networks
2.2) RNN Computational Graph
2.3) Sequence to Sequence(seq2seq)
2.4) Truncated Backpropagation Through Time
2.5) Examples
2.6) Searching for Interpretable Hidden Units
Image Captioning
Attention(cs231n_2017)
VQA(cs231n_2017)
Vanilla RNN Gradient Flow
LSTM
7.1) 모델 설명
7.2) 과정 설명
7.3) LSTM Gradient Flow

1. Process Sequences

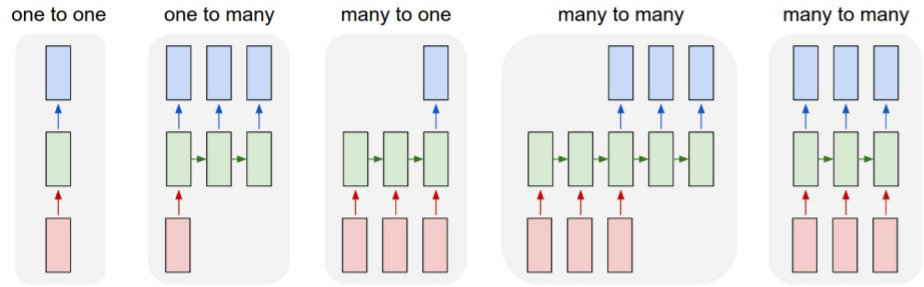
Type	Example
one to one (Feedforward Neural Networks)	Image classification	Image $\rightarrow$ Label	기존에 사용한 것과 같이 한개의 input이 한개의 output을 도출한다
one to many	Image Captioning	Image $\rightarrow$ sequence of words	이미지를 넣으면 그 이미지를 설명하는 문장(단어의 sequence)을 도출한다
many to one	Video classification	Sequence of images $\rightarrow$ label	비디오(이미지의 sequence)를 한개의 레이블로 분류한다
many to many	Machine Translation	Sequence of words $\rightarrow$ Sequence of words	번역
many to many	Per-frame video classification	Sequence of images $\rightarrow$ Sequence of labels	비디오의 프레임별로 레이블로 분류한다

1.1) Sequential Processing of Non-Sequential Data

Recurrent Neural Networks는 Non-sequential data에도 적용할 수 있다.기존에는 feedforward였던 image classification 문제를 glimpses(한 부분)들의 series를 보고 분류하는 문제로 변형하여 풀 수도 있다. 이전 glimpse(부분)을 본 것을 토대로 다음에 볼 부분을 정하고 이를 반복하여 digit을 분류하는 것이다.위와 비슷하게 매 step마다 어디에 그릴지를 정하며 digit을 생성하기도 한다.매 step마다 어떤 타입의 brush stroke를 사용할지 정하여 oil paint simulator을 만들 수도 있다.

2. Recurrent Neural Networks

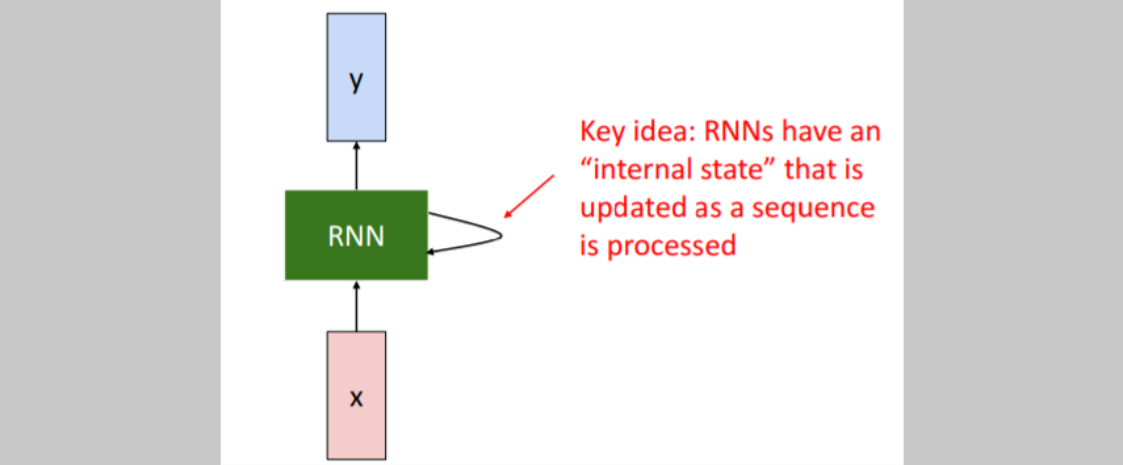RNN이 작동하는 간단한 방식을 살펴보자. 입력 x가 RNN으로 들어간다. RNN 내부에는 internal state가 있고 이 hidden state는 RNN이 새로운 입력을 받을 때마다 매번 업데이트 된다. 그리고 hidden state는 모델에 feedback되며 RNN은 매 단계마다 y값을 출력한다.

RNN이 입력을 받는다.

hidden state를 업데이트 한다.

출력값을 내보낸다.

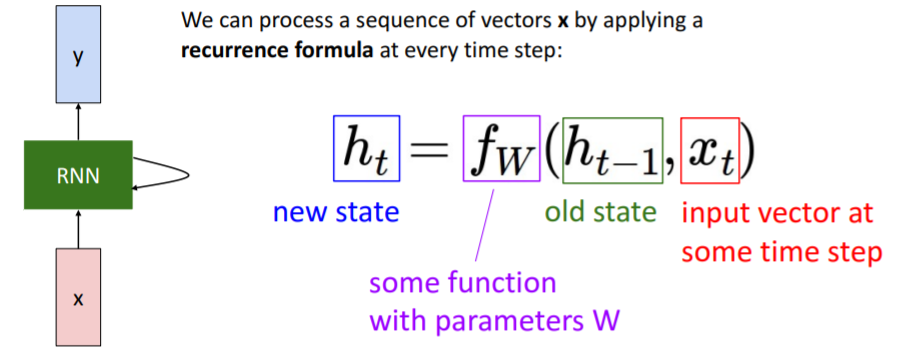RNN을 간단하게 수식으로 나타내면 위와 같다. 함수 $f$ 는 이전 단계의 hidden state인 $h_{t-1}$ 와 현재 상태의 입력인 $x_t$ 를 입력으로 받는다. 그리고 다음 상태의 hidden state인 $h_t$ 를 출력한다.

RNN에서 출력값 y를 가지려면 $h_t$ 를 입력으로 하는 FC layer을 추가해야한다. FC layer은 매번 업데이트되는 $h_t$ 를 기반으로 출력 값을 결정한다.

중요한 사실
함수 $f$ 와 parameter $W$ 는 매 step마다 동일하다.

2.1) (Vanilla) Recurrent Neural Networks

위에서 다루었던 간단한 수실을 가지고 직접 RNN을 만들어보면 바로 위 사진의 수식과 같다. weight vector $W$ 를 input $h_{t-1}, x_t$ 와 곱해주고 더해준 다음, non linearity를 위해 $\text{tanh}$ 를 적용하여 $h_t$ 를 업데이트한다.

2.2) RNN Computational Graph

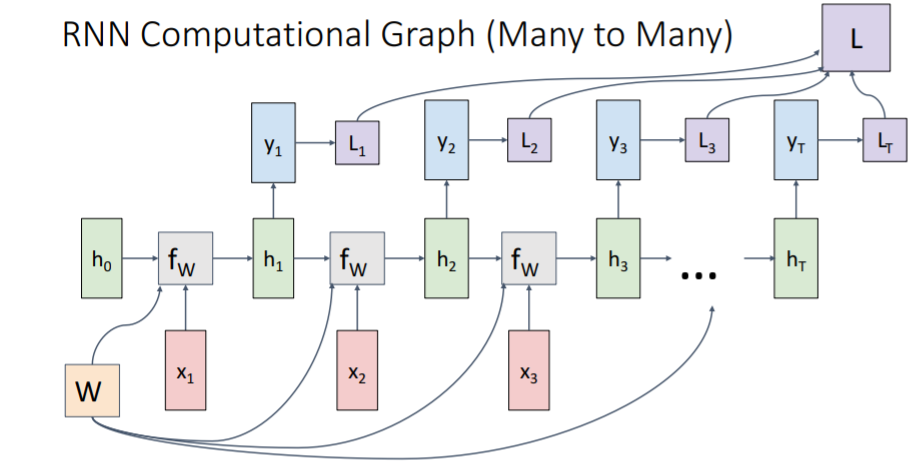$h_0$ 는 initial hidden state로, 0으로 설정된다. (학습시킬 수도 있다) 그리고 같은 weight matrix를 사용하여 input $x_1$ 과 함께 $h_1$ 로 업데이트시킨다. 매 step마다 업데이트 된 hidden state를 사용하여 $y_t$ 를 출력한다.

매 step마다 ground truth 가 있다고 가정하면 각 $y_t$ 마다 loss가 나오고, 모델의 최종 loss는 이들을 모두 더한 값이 될 것이다.

Backpropagate?

매 step마다 같은 weight $W$ 를 사용하므로 이전 backpropagte강의에서 배운 것처럼 copy state라고 할 수 있다. copy state에서의 backpropagate는 gradients를 더하여 계산했으므로 각 step의 gradients를 계산하여 weight를 업데이트 할 수 있다.

모두 같은 weight matrix를 사용하므로 sequence가 얼마나 길든 상관없이 RNN을 사용할 수 있다.

위에서 본 예시는 Many to Many였고 아래는 다른 상황에서 RNN을 사용한 Computational Graph이다.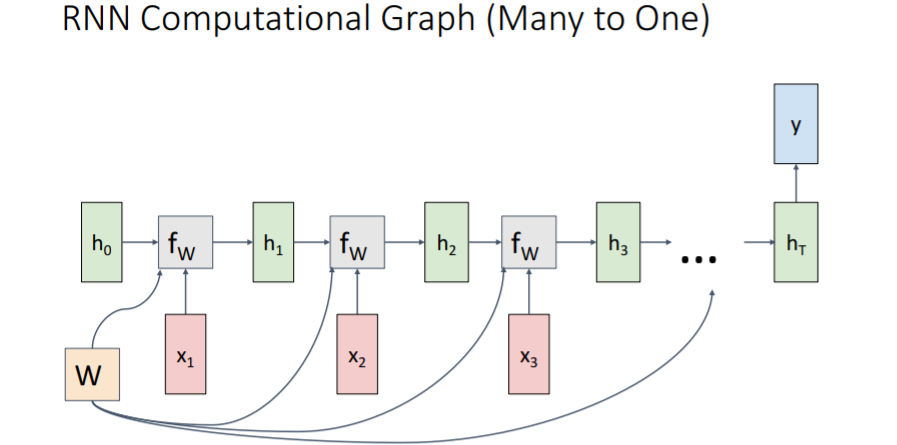

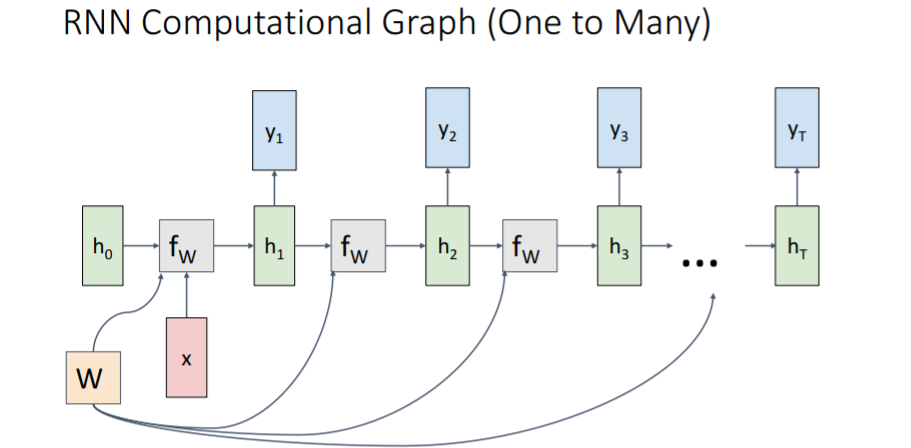
2.3) Sequence to Sequence(seq2seq)

(many to one) + (one to many)

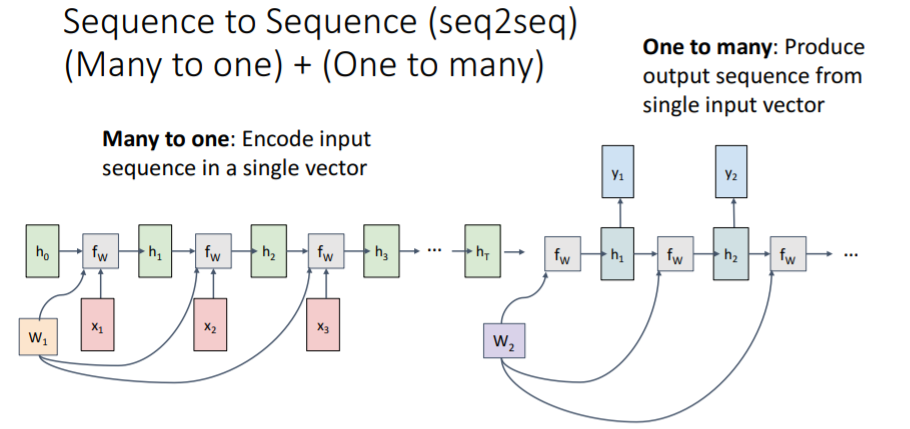Machine traslation 등에서 사용되는 모델이다. 예를 들어 영어를 프랑스어로 번역하는 task를 진행한다고 생각해보자. 영어와 프랑스어는 항상 단어들이 일대일 대응되지 않고 다른 문장 길이와 다른 단어들의 sequence로 이루어질 수 있으므로 두 개의 모델을 합쳤다.

첫번째 many to one(Encode) 모델에서는 영어 단어들을 input으로 받아서 최종 $h_T$ 를 내보낸다. 이는 그동안 입력된 input sequence들이 summarize되어 업데이트 된 hidden state라고 할 수 있다.

그러면 이를 one to many(Decode)가 받고 다른 weight matrix와 함께 프랑스어의 sequence를 출력한다.

Example: Language Modeling

어떤 charactor이 주어졌을 때 다음 charactor을 예측하여 단어를 생성하는 예제를 보자.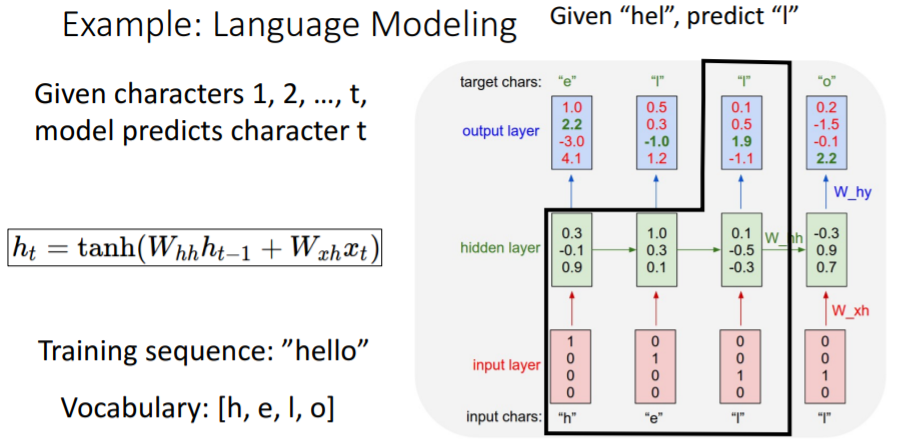hello 라는 단어를 학습시킬 것이고 각 charactor을 vector로 만들기 위해 one-hot-encoding을 시킨다.

'h'가 들어오면 hidden layer을 계산하고 이를 통해 다음 charactor인 'e'가 나오도록 학습하고, 이를 반복하여 'h', 'e', 'l', 'l'이 최종적으로 주어지면 다음에는 'o'가 나오도록 학습시킨다.

Test Time시에는 initial token인 'h'를 주고 hello를 잘 생성하는지 본다.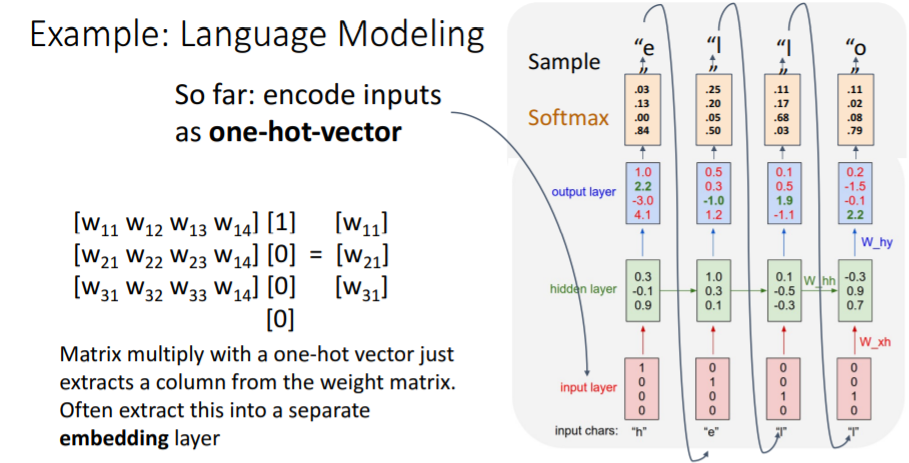hidden state를 계산할 때는 input인 one-hot-vector과 weight matrix를 곱하게 되는데 이는 결국 weight matrix의 한 column을 뽑는 것과 같다.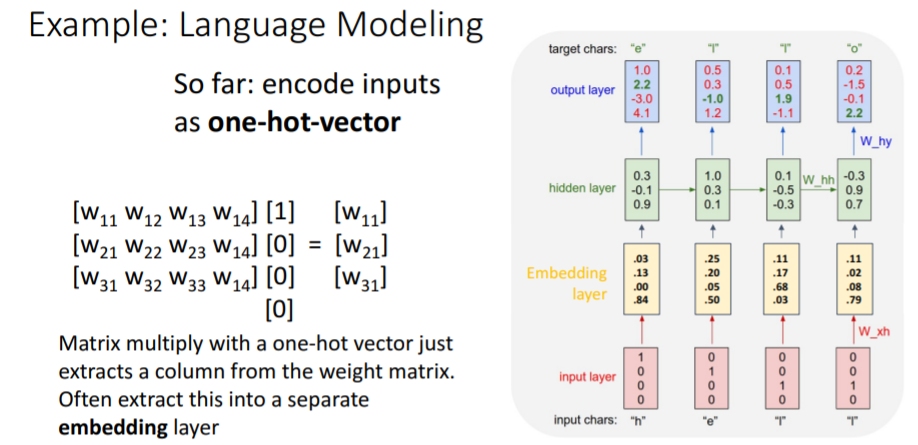따라서 hidden layer과 input layer사이에 embedding layer을 추가하여 weight matrix의 어떤 column을 뽑아야 될지를 학습할 수 있다.(이거 대체 무슨말인지 모르겠음..)

2.4) Truncated Backpropagation Through Time

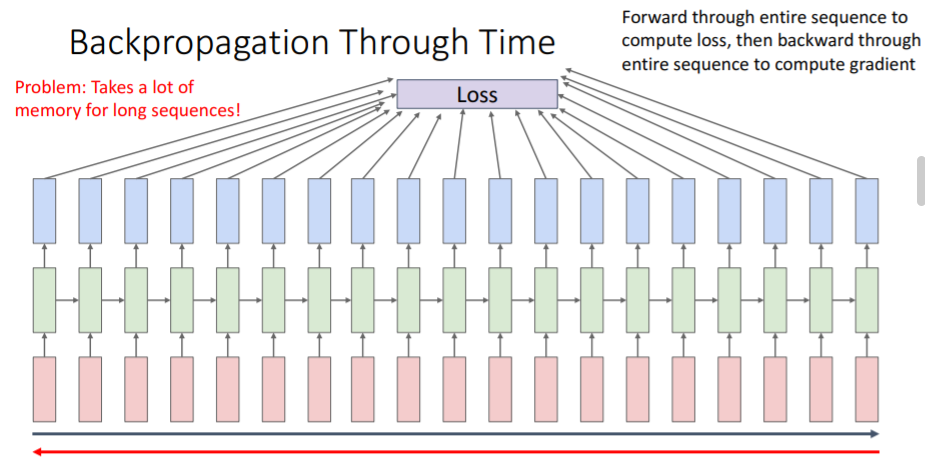sequence전체를 돌아서 loss를 계산하고 이들 전체를 다시 backpropagate시키는 과정은 매우 많은 memory와 시간을 걸리게 할 것이다. 특히 sequence 길이가 매우매우 길 수도 있기 때문이다. 이러한 문제를 해결하기 위해 approximate시키는 방법인 Truncated Backpropatgation을 사용한다.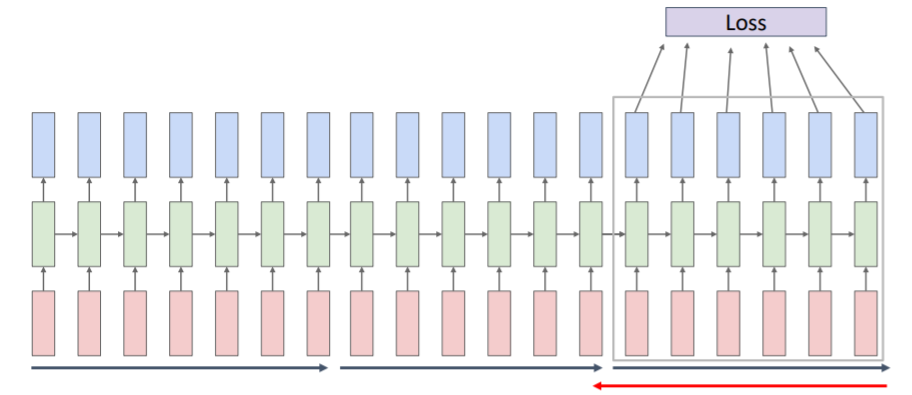전체 sequence를 모두 보지 않고 위와 같이 sequence를 100개 step정도씩 chunk들로 나누어 학습시키는 방법이다. 각 chunk당 마지막 hidden state를 기억하여 다음 chunk로 넘겨준다. 이는 hidden state는 계속 넘겨주면서도 chunk별로만 backpropagate시킬 수 있으므로 chunk 크기만큼의 GPU memory가 필요하다.

각 chunk만의 loss를 계산하고 gradient step을 진행하여 그 chunk의 weight matrix를 학습한다. 그리고 다음 chunk에서의 forward pass를 계산할 때는 이전 chunk의 hidden state를 이용한다. 즉, 다음 chunk의 initial hidden state는 이전 chunk의 final hidden state가 된다.

2.5) Examples

셰익스피어 작품의 text를 학습하여 100개 정도의 charactor을 주었을 때 다음에 나올만한 charactor을 예측한다.
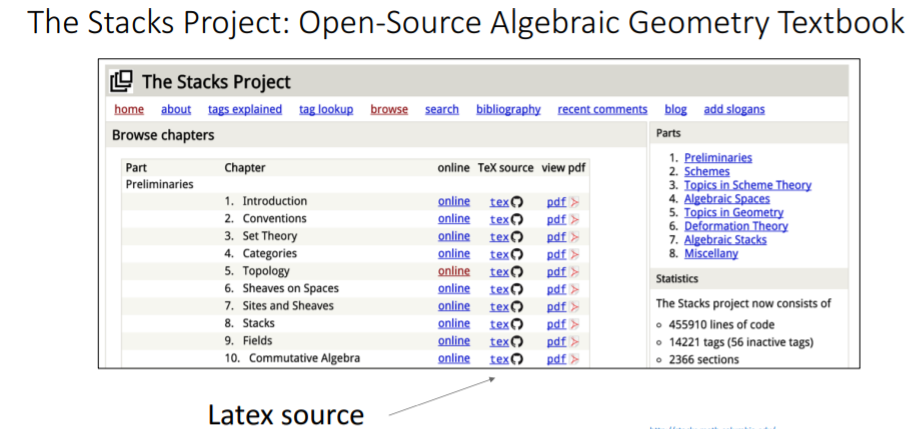
수천개의 페이지를 가진 algebraic geometry textbook의 LaTex source code를 학습시키면 아래와 같이 수학적으로는 말이 안되지만 그럴듯하게 나타난다..
리눅스 커널 소스코드를 학습시켰다.

2.6) Searching for Interpretable Hidden Units

과연 학습한 모델은 어떤 방식으로 동작하는 것일까? hidden vector을 추출해보면 해석가능한 의미있는 것들이 나올 수도 있을 것이라고 추측해보았다. 따라서 predict과정에서 hidden state를 추출하여 tanh를 거쳐 -1 ~ 1 사이의 값을 색으로 표현하여 살펴보았다.대부분의 hidden state는 아무 의미 없는 패턴으로 나타나 보인다.따옴표를 찾는 벡터에서는 따옴표 안에 있으면 파란색으로 예측된 것을 볼 수 있다.줄 바꿈을 할 때를 예측하는 것도 볼 수 있다. 줄이 점점 길어지면 빨간색으로 변하였다. 줄바꿈이 진행되면 다시 파란색으로 되었다.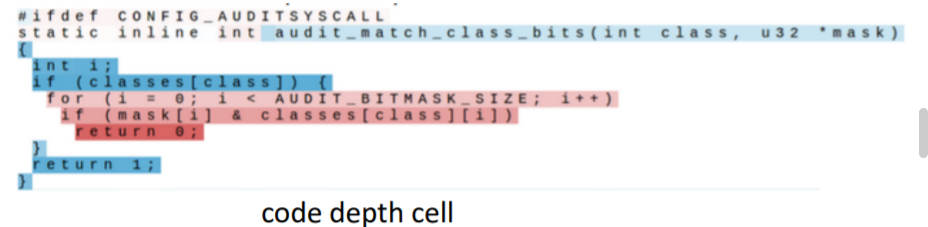위의 세개 그림은 리눅스 코드를 학습한 결과인데 if문, comments, 들여쓰기 레벨을 세는 듯한 cell을 발견할 수 있다.

그저 다음 문자를 예측하는 모델을 학습시켰을 뿐인데 결국 모델은 입력 데이터의 구조를 학습한 것이다.

3. Image Captioning

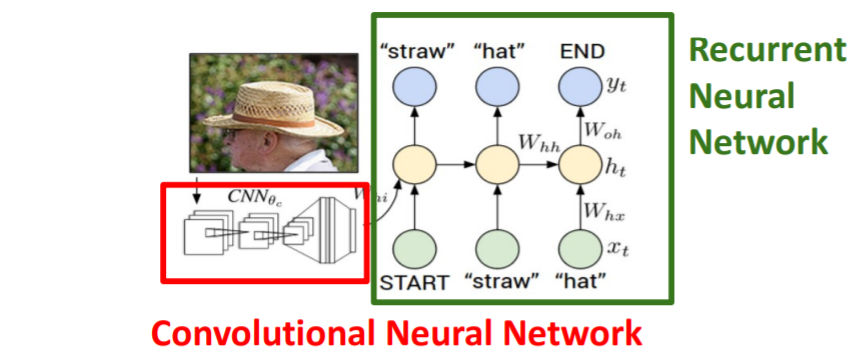이미지를 CNN에 통과시키고 CNN은 요약된 이미지 정보가 들어있는 vector을 출력한다. 이 vector은 RNN의 초기 step의 입력으로 들어간다. RNN은 captioning을 위한 문자들을 만들어낸다.우선 CNN을 transfer learning한다. 이때 마지막 두개의 layer을 떼어낸다.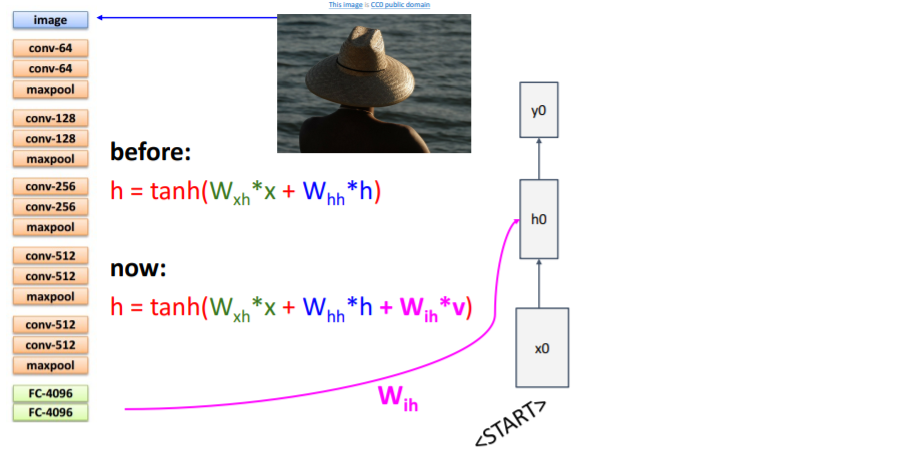이전까지의 모델에서는 RNN은 현재 step의 입력과 이전 step의 hidden state를 받고 다음 hidden state를 계산했다. 그러나 이제는 이미지 정보도 더해주어야 한다. 이를 위해 세 번째 가중치 행렬을 추가한다. CNN의 출력으로 나온 feature vector $v$ 에도 linear transform 시켜서 $W_{ih}*v$ 를 추가로 더해주었다.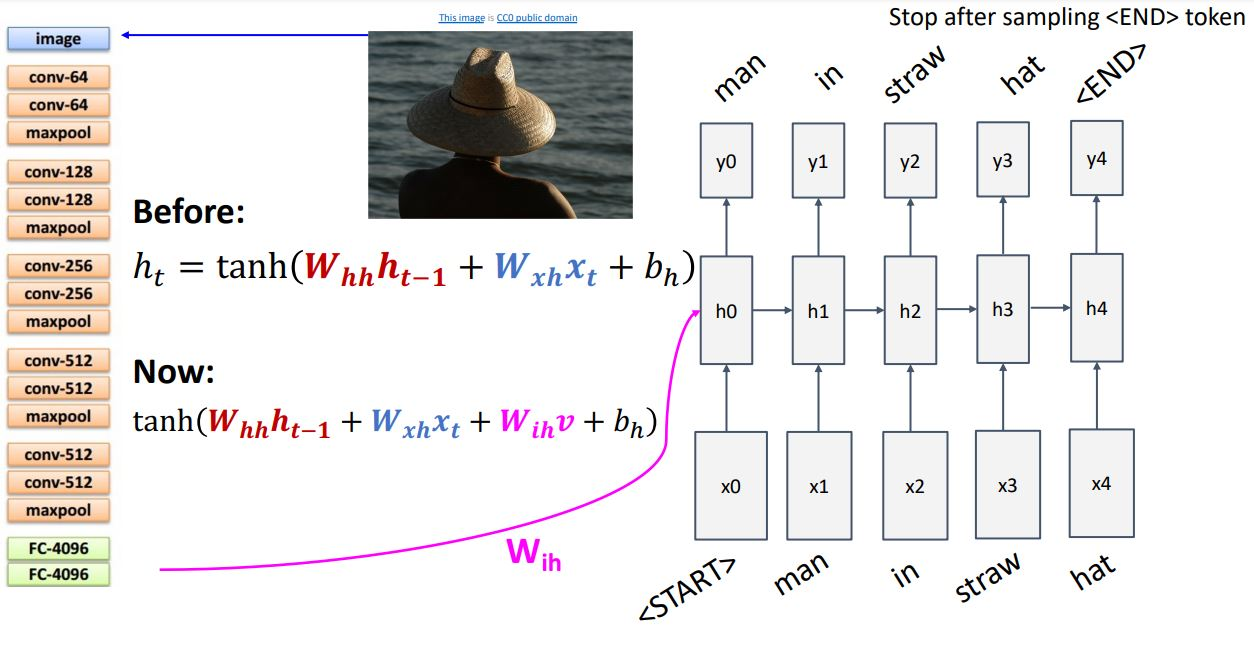RNN에서 <START>토큰으로 시작하여 <END>토큰을 출력하면 이미지 caption이 완성된다. 이를 위해 Train time에서 모든 caption의 종료지점에 이 토큰을 삽입한다.

이는 supervised learning이므로 이 모델을 학습시키려면 natural language caption이 있는 이미지를 갖고 있어야한다.

아래와 같은 결과가 도출된다.그러나 Train time에 보지 못한 데이터에 대해서는 아래처럼 엄청 잘 동작하지는 않는다.

4. Attention(cs231n_2017)

Attention은 EECS 13강에서 자세히 다룬다.

조금 더 진보된 Attention이라는 모델이 있다.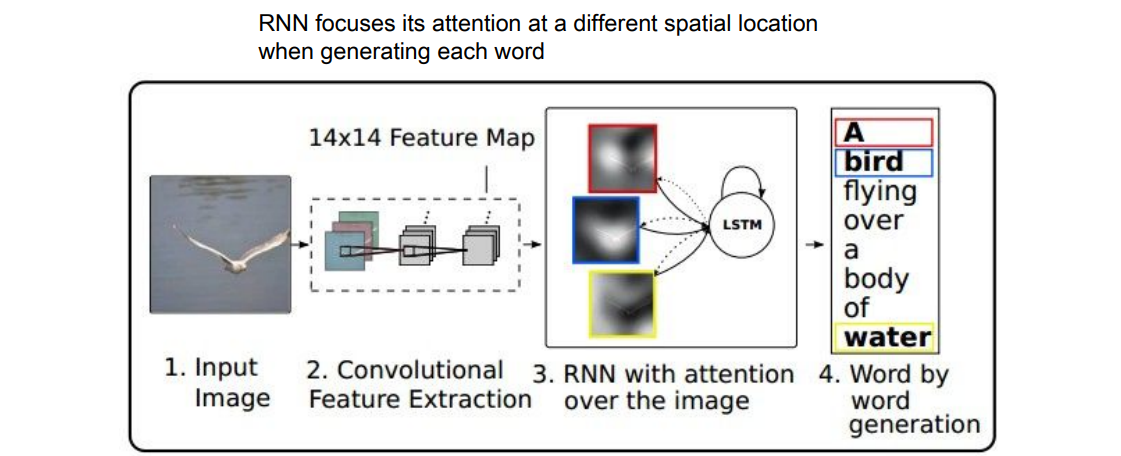 이 모델은 caption을 생성할 때 이미지의 다양한 부분을 attention하여 볼 수 있다.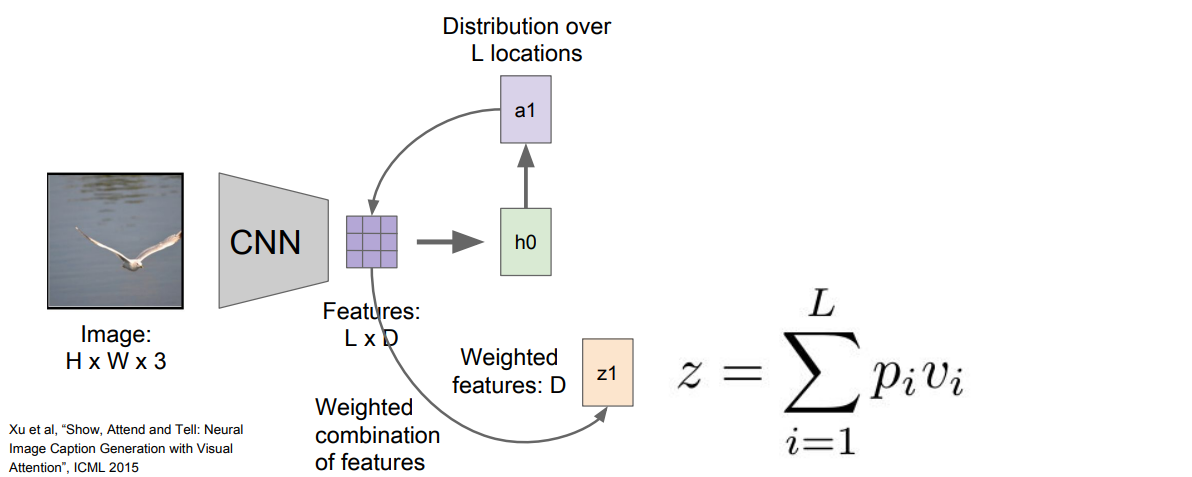우선 CNN이 있는데 CNN으로 벡터 하나를 만드는 것이 아니라 각 벡터가 공간 정보를 갖고 있는 grid of vector을 만들어낸다.

그리고 forward pass시에 매 step vocabulary에서 샘플링을 할 때 모델이 이미지에서 보고 싶은 위치에 대한 분포도 만들어낸다. 이미지의 각 위치에 대한 분포는 Train time에 모델이 어느 위치를 봐야하는지에 대한 attention이라고 할 수 있다.

첫번째 hidden state $h_0$ 는 이미지 위치에 대한 분포 $(a1)$ 를 계산한다. 그리고 이 분포 $(a1)$ 을 다시 벡터집합(Feature LxD)와 연산하여 이미지 attention $(z1)$ 을 생성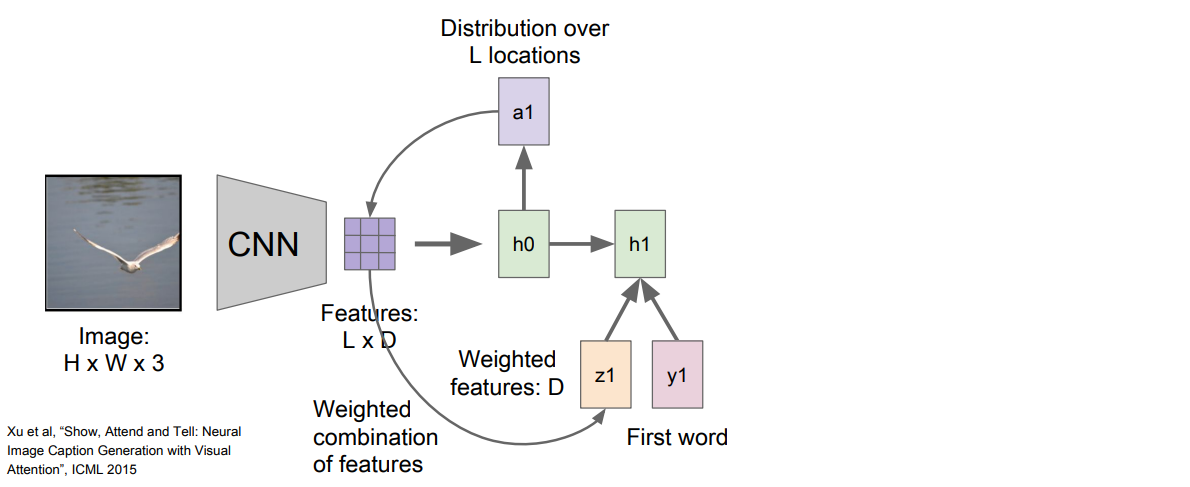한다.이 요약된 벡터 $z1$ 은 다음 step의 입력으로 들어간다. 그러면 아래와 같이 $a2$ 와 $d1$ 두개의 출력이 생성된다. 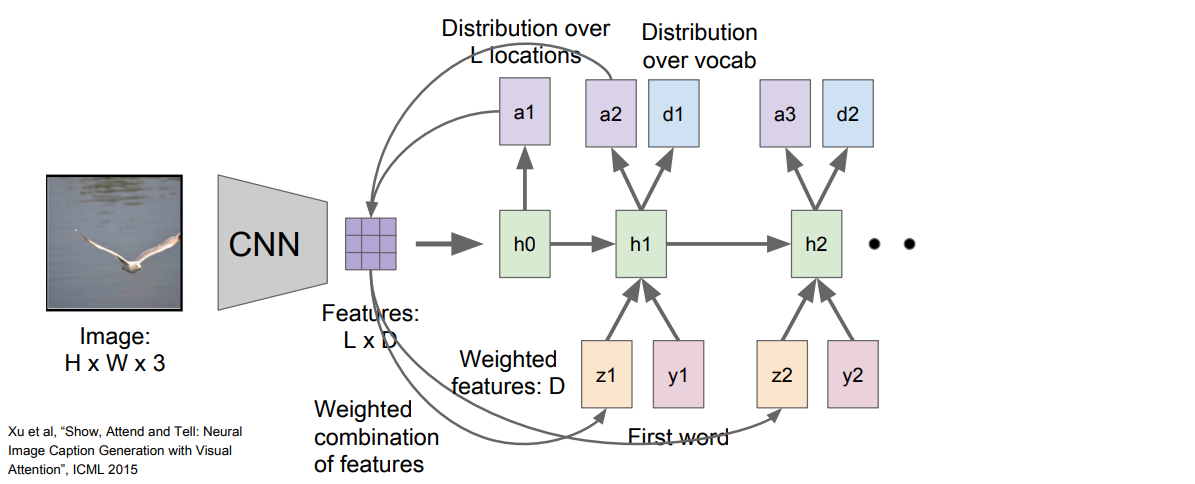$d1$ : vocabulary의 각 단어들의 분포
$a2$ : 이미지 위치에 대한 분포

이 과정을 반복하여 매 step마다 $a,d$ 가 만들어진다.Train이 끝나면 모델이 caption을 생성하기 위해 이미지의 attention을 이동시키는 모습을 볼 수 있다.결과를 보면 실제로 모델이 caption을 만들 때 의미있는 부분에 attention을 하고 있는 것을 알 수 있다.

5. VQA(cs231n_2017)

RNN+Attention 조합은 image captioning 이외에도 다양한 것들을 할 수 있다.이미지와 질문을 입력하면 모델은 네개의 보기중 정답을 맞춘다.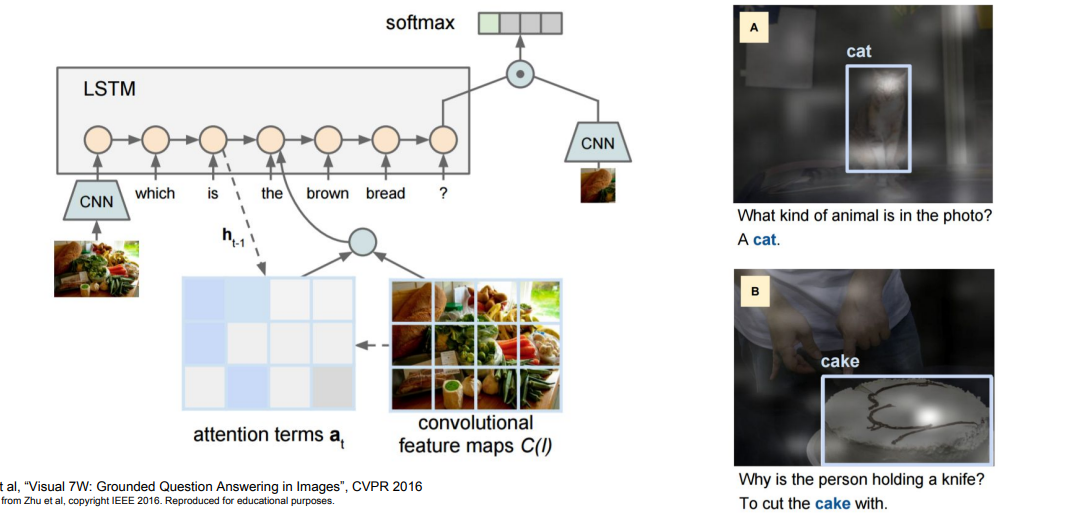모델은 자연어 문장을 입력으로 받는데 이는 RNN을 통해 vector로 요약한다. 그리고 이미지 요약을 위해서는 CNN을 사용한다. 이 둘 벡터를 concat하는 식으로 조합하면 질문에 대한 분포를 예측할 수 있다.

모델이 정답을 결정하기 위해서 이미지에 대한 attention을 만들어낸다.

6. Vanilla RNN Gradient Flow

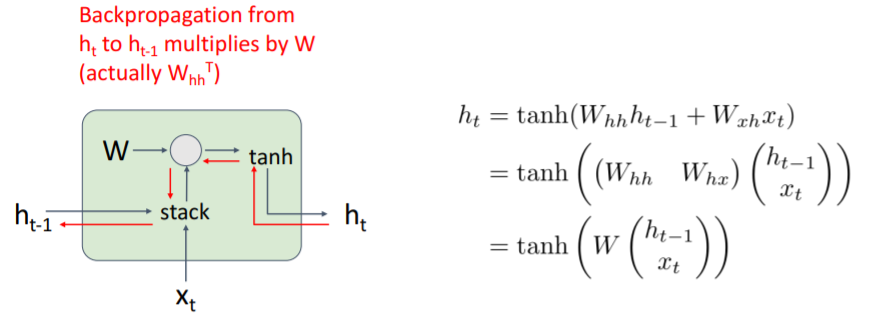$x_t$ 와 $h_{t-1}$ 을 쌓고 $W$ 와 행렬곱 연산을 한 후 tanh를 씌워서 다음 hidden state인 $h_t$ 를 만든다.

Backpropagate?

backward pass는 어떻게 이루어질까?
우선 $h_t$ 에 대한 loss의 미분값을 얻는다. 그리고 loss에 대한 $h_{t-1}$ 의 미분값을 계산하게 된다. 이 과정에서 두 가지 문제가 발생한다.

tanh는 non-linearity에서 좋지 않지만 옛날에 나왔으므로 그렇다고 치자.
$W$ 와 행렬곱 하는 gate에서 backprop은 결국 $W$ 의 transpose를 곱하게 되는데 ( $W_{hh}^T$ ) 아래와 같이 만약 여러 sequence의 cell을 쌓아올리는 사실을 고려하면 결국 매번 같읕 $W_{hh}^T$ 를 곱하여 backprop을 하게 된다.

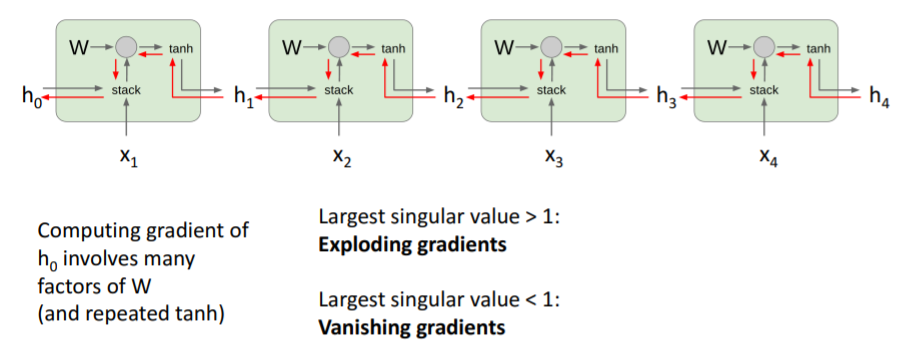만약 수백개의 cell들이 있다고 하면 $W_{hh}^T$ 의 같은 값들을 수백번 곱해야한다. 여기에서 문제가 두개 발생하는데,

만약 곱해지는 값(간단하게 가장 큰 singular value(특이값)으로 함)이 1보다 큰 경우라면, gradient가 터진다.
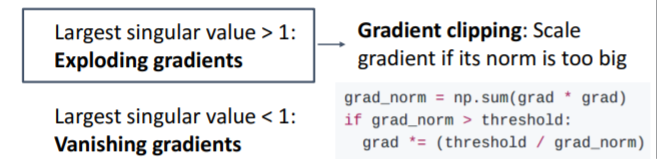
1보다 작은 경우라면 gradient가 작아져 결국 0이 된다.

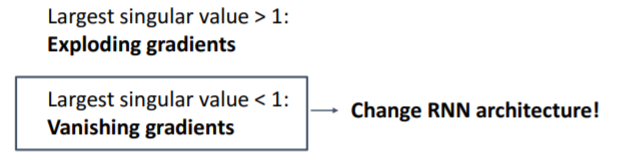
두 상황을 피하기 위해서는 곱해지는 값이 1인 경우밖에 없다.

7. LSTM

위와 같은 상황을 해결하기 위해 LSTM이라는 방식이 고안되었다.

7.1) 모델 설명

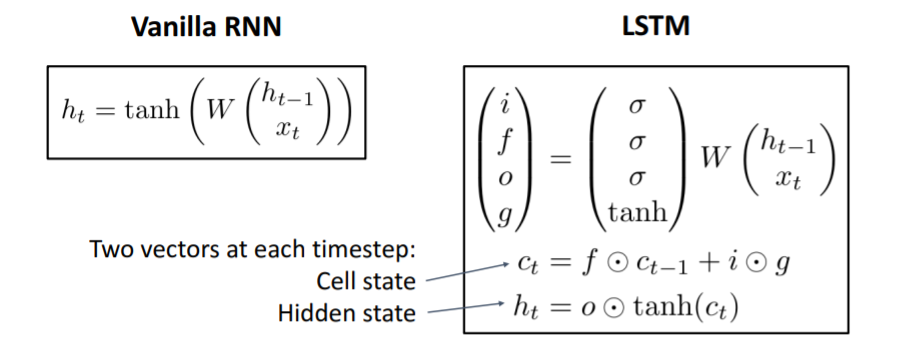
LSTM에는 한 cell 당 2개의 hidden state가 있다. $h_t$ 는 vanilla RNN에서의 것과 유사한 개념이다. 하지만 LSTM에는 $c_t$ 라는 두번째 벡터 cell state가 있다.

LSTM도 두 개의 input $h_{t-1}, x_t$ 를 받는다. 그리고 4개의 gates $i,f,o,g$ 를 계산한다. 이 gates를 $c_t$ 를 업데이트하는데 이용하고 $c_t$ 를 사용하여 다음 step의 hidden state를 업데이트한다.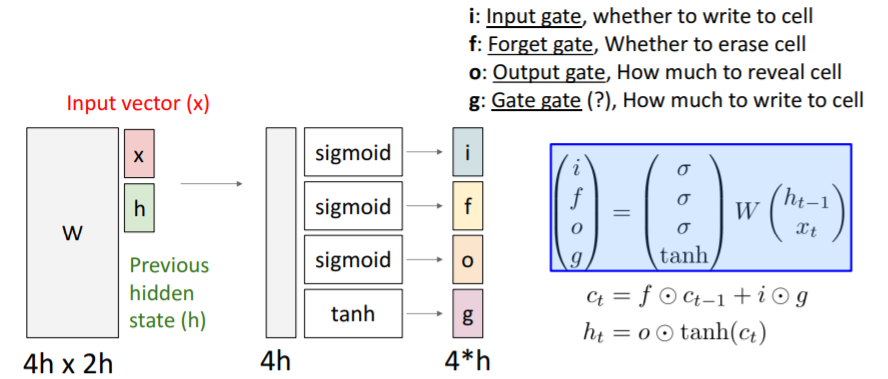과정을 자세히 살펴보자.

우선 이전 hidden state $h_{t-1},x_t$ 를 입력받는다.
vanilla RNN에서는 이들을 concat한 후 커다란 $W$ (사실 4개의 가중치 행렬)와 행렬곱한 후 tanh를 통과시켜 $h_t$ 를 직접 계산하였지만, LSTM에서는 concat하고 $W$ 와 행렬곱한 결과를 4개의 gates로 출력한다.
gates는 hidden state의 크기와 같다.

gates	설명
i: input gate	cell에서의 입력 $x_t$ 에 대한 가중치이다.
f: forget gate	이전 step의 cell 정보를 얼마나 망각할지에 대한 가중치이다
o: output gate	cell state( $c_t$ )를 얼마나 밖에 드러내 보일지에 대한 가중치이다.
g: gate gate	input cell을 얼마나 포함시킬지 결정하는 가중치이다.

각 gates에서 사용되는 non-lineariy도 다른데, i, f, o에서는 sigmoid를 사용한다. 즉 gate값이 0 ~ 1 이다.

g는 tanh 즉, -1 ~ 1의 값을 갖는다.

7.2) 과정 설명

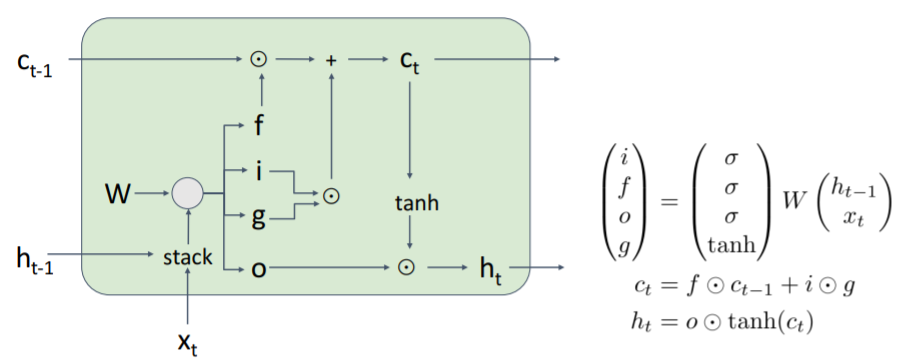과정을 자세히 보자. 이전 step의 cell state( $c_{t-1}$ )은 forget gate와 element-wise multiplication을 한다. f가 0이면 이 결과는 0이 되어 이전 cell state를 잊고 반면 f가 1이면 결과가 1이 되어 이전 cell state를 계속 기억한다.

i와 g의 element-wise mul에서 g는 -1 ~ 1의 값이므로 값을 뺄지 더할지를 결정한다. i는 0 ~ 1의 값이므로 크기를 결정한다. 따라서 이 결과는 $W(h_{t-1},x_t)$ 값을 cell state에 얼마나 반영할지 정한다.

마지막으로 o와 tanh( $c_t$ )를 element-wise mul하여 $h_t$ 를 구한다. 이는 $c_t$ 에서의 0 ~ 1 사이의 값인 $W(h_{t-1},x_t)$ 을 통해 원하는 element만 내보내는 필터링 된 결과를 만든다. 그리고 이 값도 다음 cell로 넘어간다. output gate는 다음 hidden state를 게산할 때 cell state를 얼마나 노출시킬지 결정한다.

7.3) LSTM Gradient Flow

이전 vanilla RNN에서는 backward pass시 동일한 가중치 값을 계속 곱해지는 문제가 있었다. 그러나 LSTM에서는 cell state의 gradient를 계산하는 backward경로를 보면 상황이 나아졌다.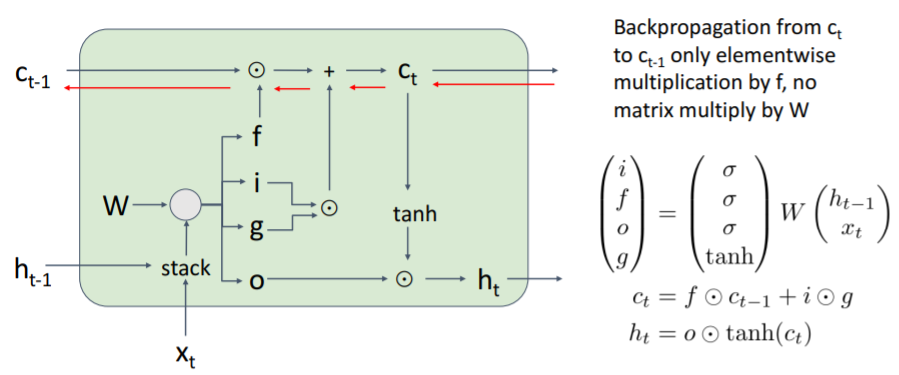우선 add에 대한 backprop이 있다. add에서는 upstream gradient가 두 갈래로 복사된다. 따라서 element-wise노드로 직접 전달된다. 결과적으로 gradient는 upstream gradient와 forget gate의 element-wise 곱이다.

cell state의 backprop은 그저 upstream gradient * forget gate이다.

이 특성은 vanilla RNN에 비해 좋은 점이 2개 있다.

forget gate와 곱해지는 연산이 element-wise라는 것이다.
element-wise 곱을 통해 매 step다른 값의 forget gate와 곱해질 수 있다. 이는 기존에 같은 가중치 행렬을 계속 곱한것과 달리 매 step마다 변하는 forget gate를 곱하므로 gradient exploding/vanishing을 더 쉽게 해결할 수 있다.

또한 forget gate는 sigmoid에서 나온 값이므로 element-wise곱이 0 ~ 1사이의 값이다. 이에 따라 더 좋은 수치적 특성을 보일 수 있다.

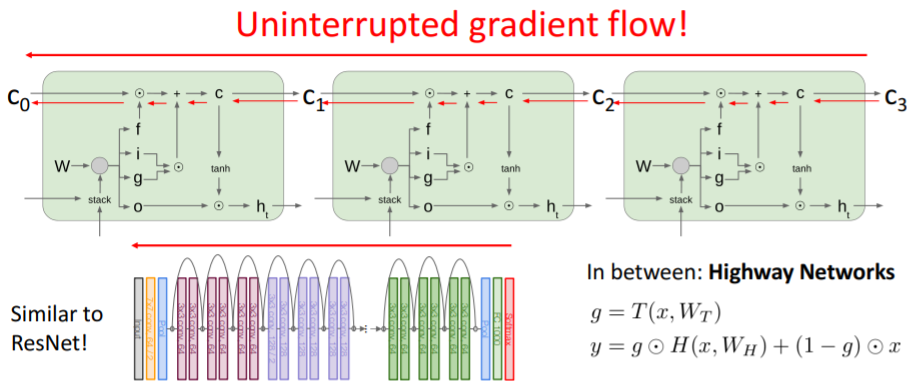cell state에 대한 gradient는 마치 고속도로처럼 아주 깔끔하게 backprop되는 것을 볼 수 있다.