[EECS 498-007 / 598-005] 강의정리 - 17강 3D Vision

ONground·2022년 4월 29일

EECS 498-007 / 598-005

[CS231n] + [EECS 498-007 / 598-005]

목록 보기

14/17

3D Vision

3D Vision topics
3D Shape Representations
2.1) 3D Shape Representations: Depth Map
2.2) 3D Shape Representations: Surface Normals
2.3) 3D Shape Representations: Voxels
2.4) Scaling Voxels
2.5) 3D Shape Representations: Implicit Functions
2.6) 3D Shape Representations: Point Cloud
2.7) 3D Shape Representations: Triangle Mesh
Shape Comparison Metrics
3.1) Shape Comparison Metrics: Intersection over Union
3.2) Shape Comparison Metrics: Chamfer Distance
3.3) Shape Comparison Metrics: F1 Score (Best)
3.4) Summary
Cameras
4.1) Cameras: Canonical vs View Coordinates
4.2) View-Centric Voxel Predictions
3D Datasets
5.1) 3D Datasets: Object-Centric
3D Shape Prediction: Mesh R-CNN
6.1) Mesh R-CNN: Hybrid 3D shape representation
6.2) Mesh R-CNN Pipeline
6.3) Mesh R-CNN Results

Summary

1. 3D Vision topics

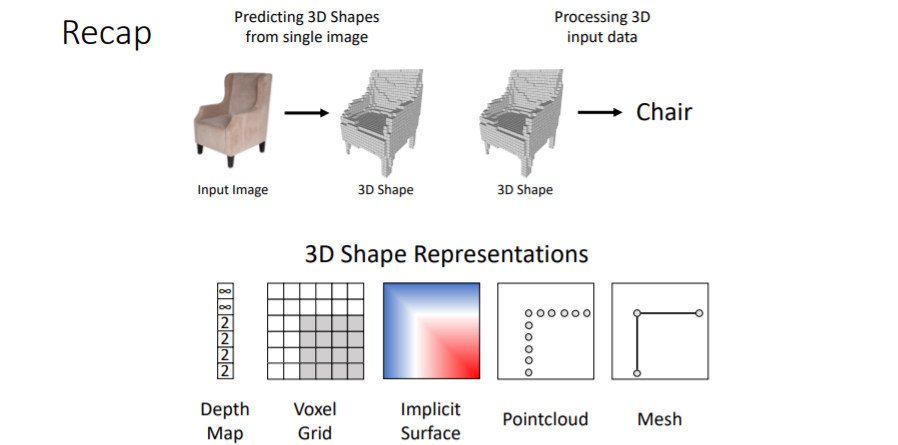
많은 topics가 있지만 이 강의에서는 2가지 problems에 대해 다룬다.

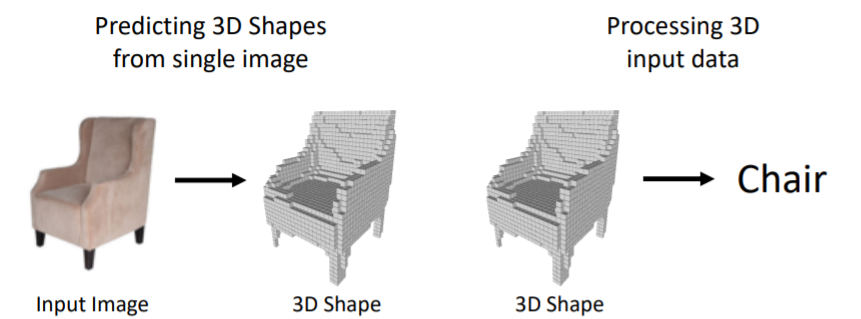
왼쪽에서 처럼 2d input 이미지를 가지고 3d shape를 predict하는 것
3d shape를 input으로 넣어서 이를 classification/segmentation 하는 것

그리고 모두 fully supervised로 학습하는 과정에 대해 배울 것이다.3D Vision에는 매우매우매우 많은 topics가 존재한다.

2. 3D Shape Representations

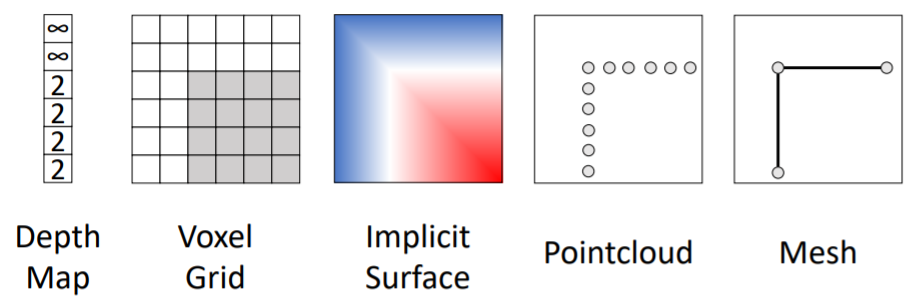3D shape를 나타내는 방법은 5개의 다른 방식으로 나타낼 수 있다. 이들에 대해 자세히 알아보도록 하자.

2.1) 3D Shape Representations: Depth Map

Predicting Depth, Surface Normals and Semantic Labels with a Common Multi-Scale Convolutional Architecture 논문

Depth Map은 각 pixel에 대해 camera와 pixel사이의 거리를 assign한다.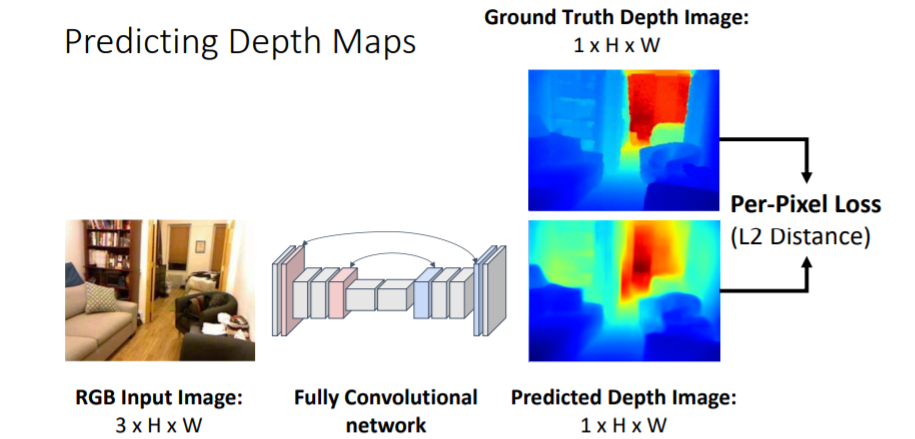Semantic Segmentation에서 했던 것 처럼 Fully Convolutional network를 사용하여 pixel별로 계산할 수 있다. 이를 통해 Predicted Depth Image와 GT image와의 Per-pixel loss를 계산하여 학습할 수 있다.

그런데 문제점이 있다.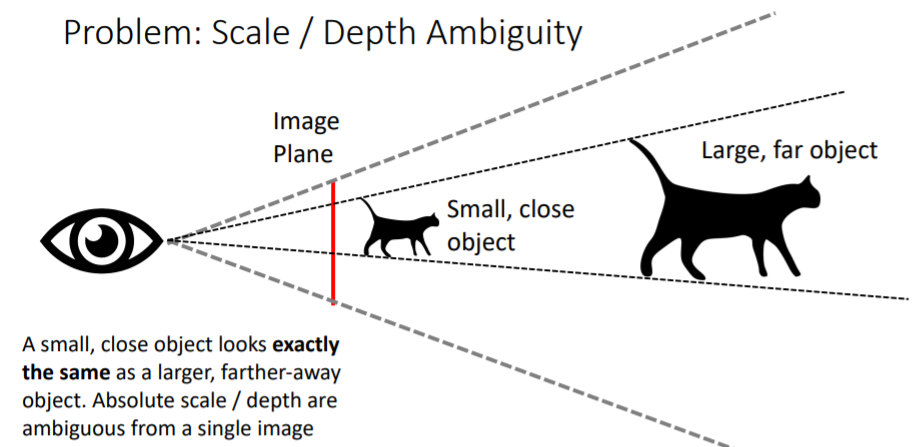하나의 이미지가 주어졌을 때 우리는 작고 가까이 있는 물체와 크고 멀리 있는 물체를 구분할 수 없다. 예를 들어서 크기1인 고양이와 크기2인 2배멀리있는 고양이는 정확히 같게 보인다.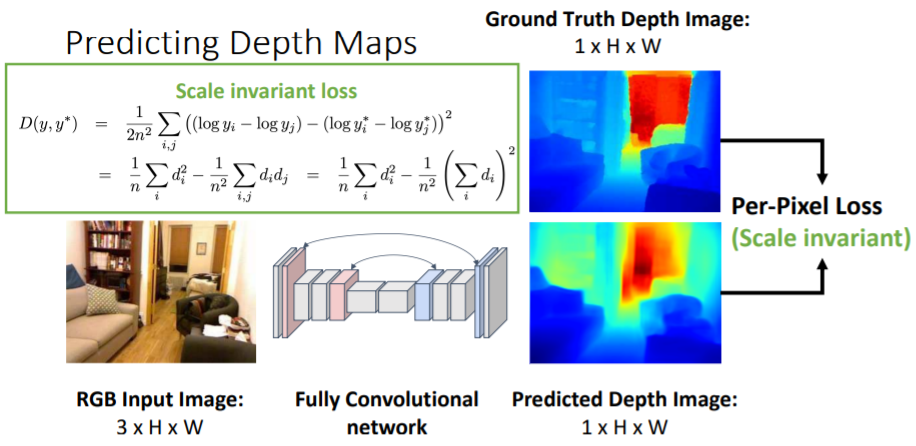Scale / Depth Ambiguity문제를 해결하기 위해 Scale invariant loss를 사용한다.

왜 이 loss가 문제를 해결해주는지에 대한 자세한 내용은 논문에서 확인하라고 한다.

Depth Map Prediction from a Single Image using a Multi-Scale Deep Network 논문

https://deeesp.github.io/deep%20learning/SI-SE/

2.2) 3D Shape Representations: Surface Normals

Predicting Depth, Surface Normals and Semantic Labels with a Common Multi-Scale Convolutional Architecture 논문

각 pixel에 orientation(방향) of the surface of that object를 assign한다. 예를 들어 위 그림의 normals를 보면 파란색은 윗방향(침대 위를 보면.)을 나타내고 붉은색은 앞쪽방향, 초록색은 왼쪽방향 등을 나타내는 것을 볼 수 있다.input 이미지가 들어오면 fully convolutional network를 통과시켜 각 픽셀당 3-dim vector을 계산한다.

그리고 GT Normals와 픽셀별로 각 픽셀에 해당하는 vectors의 angles(각도)를 비교한다.

Depth map과 Surface Normals의 문제점

occluded(가려진) 부분에 대해서는 알 수 없다. 따라서 사실상 2.5D 이미지라고 불리운다.

2.3) 3D Shape Representations: Voxels

Voxel은 개념적으로 간단하다. 3d 세상을 3d grid로 나타내고, 물체가 있는 곳은 on시킴으로써 3d로 표현할 수 있다(마인크래프트를 생각해보자).

그러나 문제점은

디테일이 살아있는 3d object를 생성하기 위해서는 high spatial resolution of 3d voxel이 필요하다(더 촘촘한 3d grid가 필요하다).
high resolution으로 확장하는 것은 쉬운 일이 아니다.

2.3.1) Processing Voxel Inputs: 3D Convolution

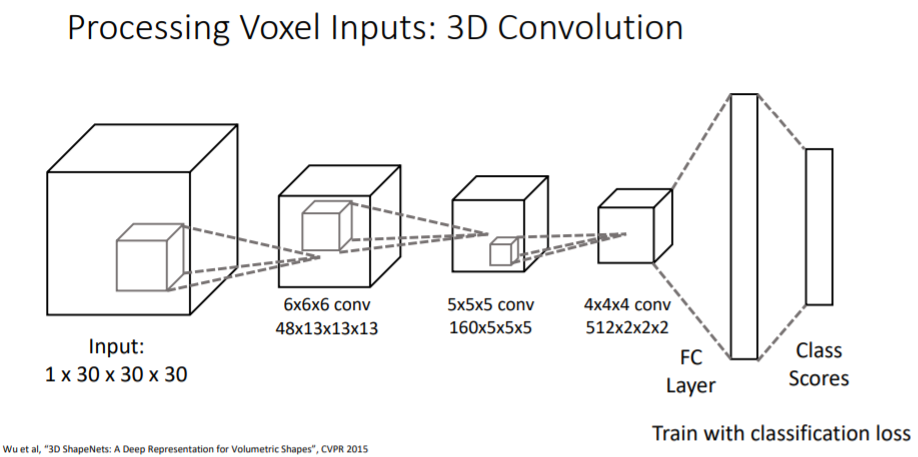voxel input이 주어졌을 때 그 voxel이 의자인지, 비행기인지 등을 classification하는 것은 쉽다. 3d convolution을 활용하여 계산한다. kernel이 3d이다.

Input tensor 차원에 대해 설명하면

1은 channel이고 30x30x30은 공간 차원이다.
1channel은 3d voxel grid가 채워져있는지 아닌지에 대한 것을 나타내는 feature이다.

2.3.2) Generating Voxel Shapes: 3D Convolution

3D-R2N2: A Unified Approach for Single and Multi-view 3D Object Reconstruction 논문

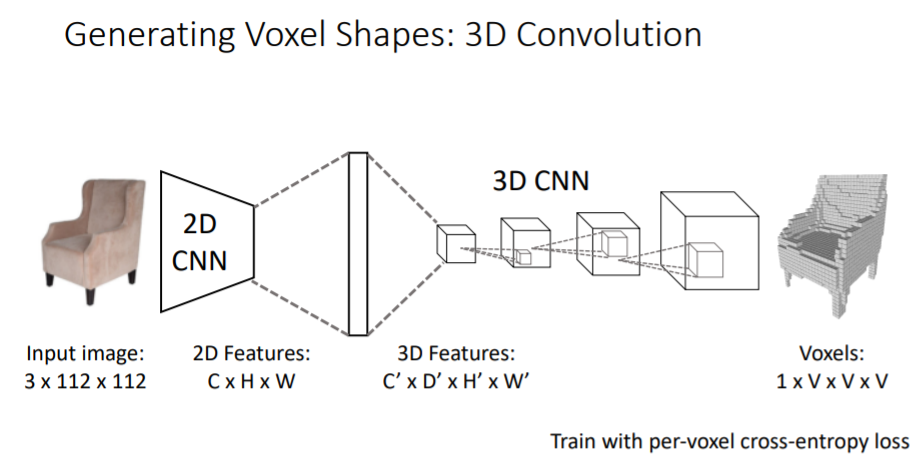그동안은 voxel을 input으로 받았지만 여기에서는 input이미지를 받아서 voxel grid를 predict한다.

Input (Image)	Output (Voxels)
3(RGB) x (112 x 112)	1(Voxel grid ON/OFF) x (V x V x V)
RGB 2차원 이미지	voxel grid로 이루어진 3차원 voxel grid

따라서 output을 만들기 위해서는 새로은 extra spatial dimension이 필요하다(2차원에서 3차원을 생성해야하므로).

그리고 voxel grids를 predict하는 쉬운 방법 중 하나는 3d와 4d tensor간의 차이를 fc-layer을 통해서 계산하는 것이다.

input이미지에 대해 2D CNN을 통과하고 나면 CxHxW의 3d feature map이 나오고 이를 큰 하나의 vector로 flattening시킨다. 그리고 fc-layers를 통해 4d tensors로 reshape시켜준다. 여기에서부터 3D CNN을 가지고 upsampling시켜주어 최종 voxel grid를 생성한다.

그러나 계산이 매우 많은 문제가 있다.
3D Convolution은 매우 매우 많은 계산을 필요로 한다.

2.3.3) Generating Voxel Shapes: ”Voxel Tubes”

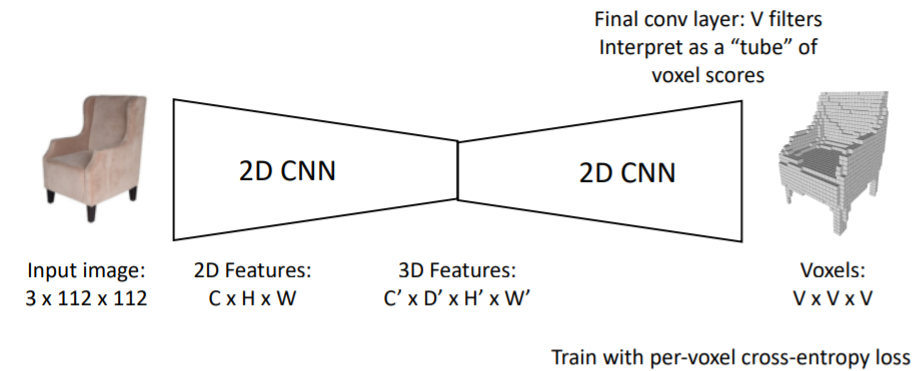3D Conv의 계산 문제를 해결하기 위해 2D Conv만을 사용하는 방법도 나왔다.

마지막 output에서 trick을 사용하는 방식인데 잘 이해가 안돼서 다시 봐야할 것 같다.(26'')

마지막 output에서 기존 C를 담당하던 차원을 V filter이 함께 수행하도록 하는듯. 1xHxWxD => VxVxV

2.3.4) Voxel Problems: Memory Usage

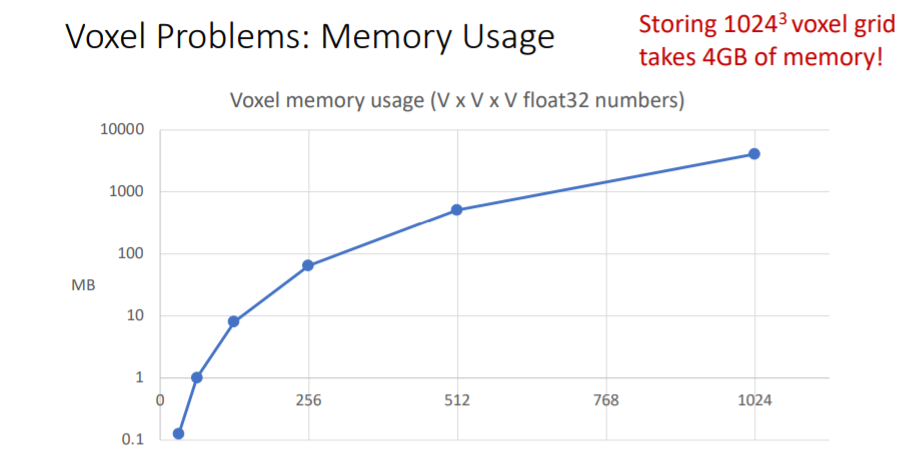high resolution voxel grid를 얻기 위해서는 많은 메모리가 필요하다. 따라서 very high spatial resolutions에서는 naive voxel grids를 사용하기에 적합하지 않다.

그러나 voxel grid를 higher spatial resolutions로 scaling하는 방법들이 있다.

2.4) Scaling Voxels

2.4.1) Oct-Trees

Octree Generating Networks: Efficient Convolutional Architectures for High-resolution 3D Outputs 논문

voxel grid를 multiple resolution으로 표현하는 방법이다.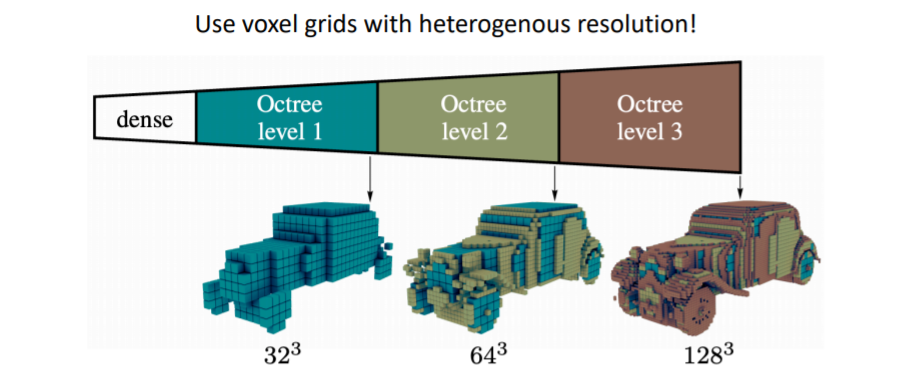이를 통해 coarse voxels를 생성하고 세부적인 디테일은 fine voxels(higher resolution)을 사용하여 표현한다.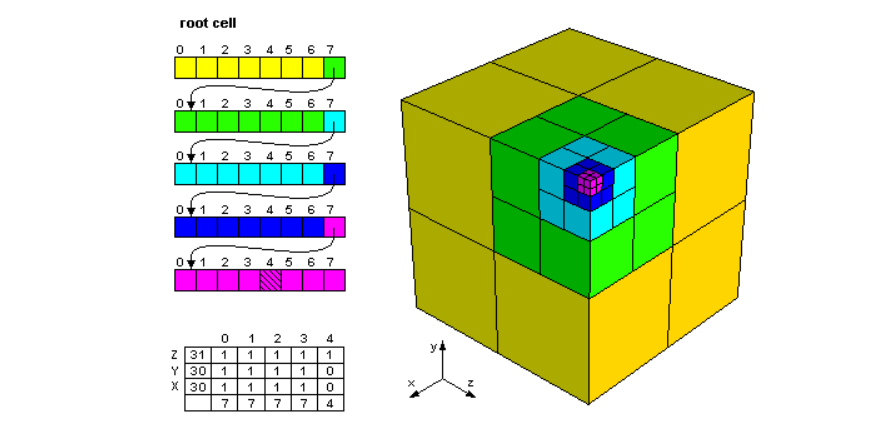

2.4.2) Nested Shape Layers

Matryoshka Networks: Predicting 3D Geometry via Nested Shape Layers 논문

Full 3d shape를 dense voxel grid로 전부 표현하기 보다 겉의 fine voxel에서 속 안의 보이지 않는 dense voxel을 빼고, 다시 조금 내부의 fine voxel을 더하고, 그 속을 빼고 이런 과정을 반복한다.

2.5) 3D Shape Representations: Implicit Functions

Occupancy Networks: Learning 3D Reconstruction in Function Space 논문

이 방식은 3d shape를 함수로 표현하는 방식이다.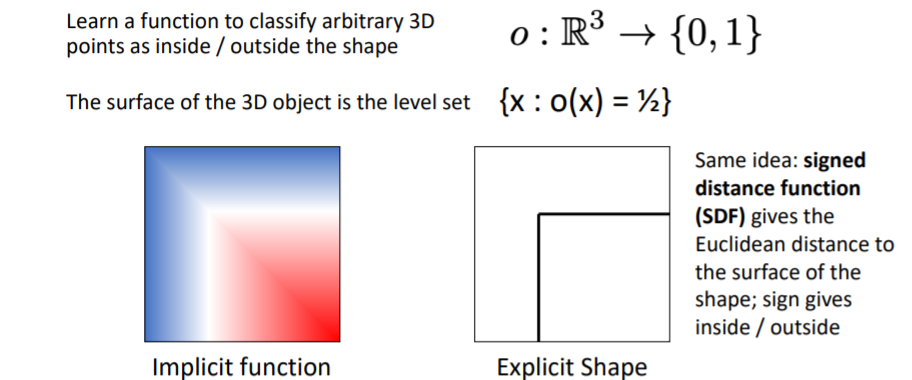3d space의 어떤 좌표값을 input으로 넣으면 그 좌표가 object로 채워져있는지 아닌지에 대한 확률(물체의 inside인지 outside인지)을 output으로 출력한다. (probability that position that arbitrary position is either occupied or not occupied by the object.)

object의 외부 표면(exterior surface)은 $\{x:o(x)={1\over 2}\}$ 를 만족하는 level set(레벨 집합)이다. 즉 값이 0.5가 나오는 모든 좌표들의 집합은 표면을 나타낸다.

(level set의 예시를 보면 $f(x,y,z)=c(\text{상수})$ 를 만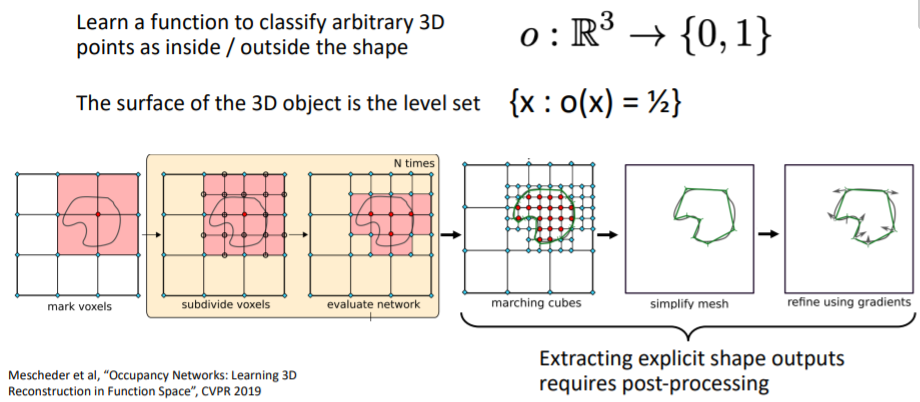족하는 모든 $\{x,y,z\}$ 집합이다. 참고)3d voxel grid등으로 implicit function을 학습하고 이를 explicit하게 표현하여 물체의 표면을 확인할 수 있다.

2.6) 3D Shape Representations: Point Cloud

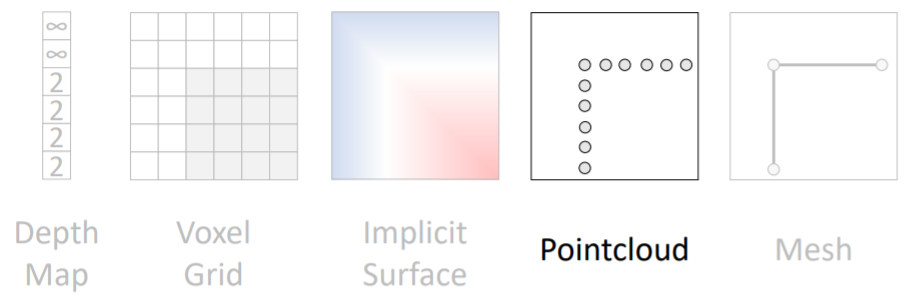
3d shape를 points들의 집합으로 표현한다.

point cloud는 voxel grid보다 좀 더 쉽게 조정이 가능하다.
voxel grid에서 fine detail을 위해서는 high resolution이 필요했다. 하지만 point cloud에서는 우리가 디테일을 살리고 싶은 부분에만 더 많은 points를 할당해주면 된다.
그러나 points는 매우 작기 때문에 point cloud를 명시적으로 나타내려면 points를 공크기로 부풀려서 렌더링해야한다(post-processing이 필요함).

2.6.1) Processing Pointcloud Inputs: PointNet

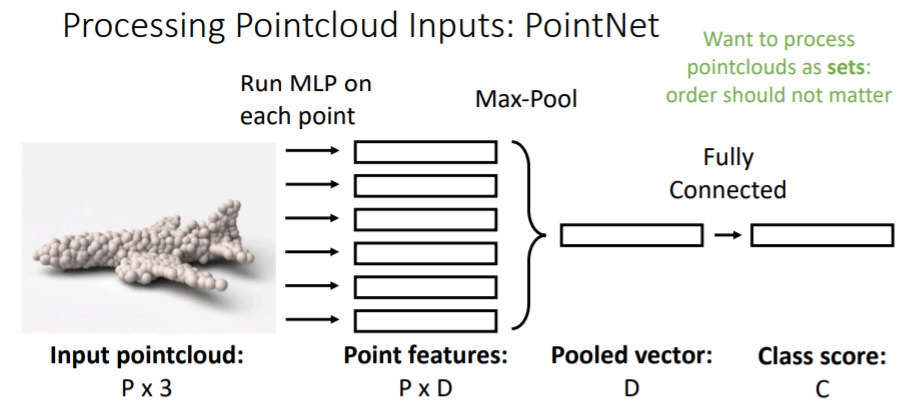point cloud로 된 input을 받는다(P개의 points x 3(x,y,z 좌표)). 그리고 이를 가지고 classification을 한다.

여기에서 흥미로운 점은 pointcloud input에서 P points set은 순서가 중요하지 않다.

학습과정을 살펴보면,
(x,y,z)좌표가 있는 각각의 point들을 독립적으로 작은 MLP에 넣는다. 즉 P개의 작은 MLP에 독립적으로 연산시킨다. 그리고 D차원의 point feature을 얻는다.

이들을 전부 Max pooling하여 D차원의 feature vector(pooled vector)을 만든다. 이를 fc-layer에 연결하여 class score을 구한다.

위의 방식은 하나의 매우 간단한 연산 층을 나타낸 것이고 보통 실제로는*
pooled vector**을 갖고와서 다시 모든 point features vector과 concatenate하고 다시 작은 MLP에 독립적으로 넣고 또 여러가지 Pooling을 거치는 과정을 반복한다.

2.6.2) Generating Pointcloud Outputs

A Point Set Generation Network for 3D Object Reconstruction from a Single Image 논문

이 방식은 pointcloud output을 생성하는 방식이다.
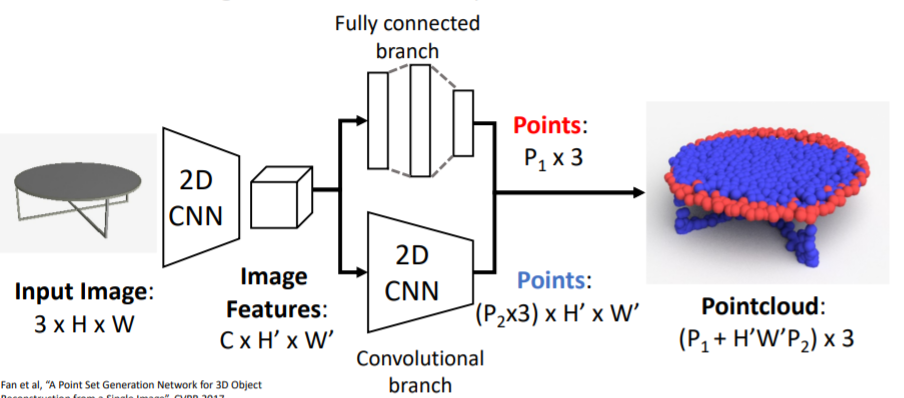RGB이미지를 input으로 넣어서 3d shape를 나타내는 pointcloud를 출력한다.

이 모델은 설명 없이 넘어갔다.

2.6.3) Predicting Point Clouds: Loss Function

predicted point cloud와 GT point cloud 사이의 Loss를 계산하는 방식을 소개한다. pointclouds를 sets로 비교하고, 미분가능한 Loss가 필요하다.
We need a (differentiable) way to compare pointclouds as sets!

pointclouds를 비교할 때( $S_1, S_2$ 를 비교) 보통 Chamfer distance를 사용한다.

Chamfer distance

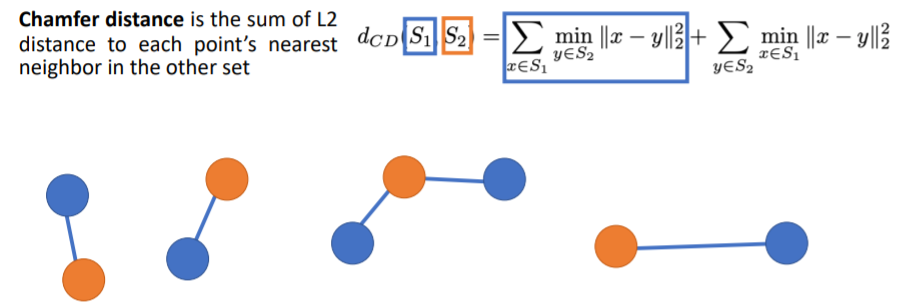d_{CD}(S_1,S_2)=\sum_{x \in S_1}\min_{y\in S_2}\lVert x-y \rVert_2^2+\sum_{y\in S_2}\min_{x\in S_1}\lVert x-y\rVert_2^2

우선 2 sets of points를 input으로 식에 넣는다( $S_1, S_2$ ). 이 두개의 point sets는 파란색 집합과 오렌지색 집합이다. chamfer distance는 이 두개의 sets of points가 얼마나 다른지를 나타내준다.

먼저 식에서 첫번째 term은 각 blue points에 대해 가장 가까운 orange point(nearest neighbor orange point)를 찾아서 둘 사이의 Euclidean distance를 계산한다. 그리고 이들 거리를 모두 더하는 과정이다.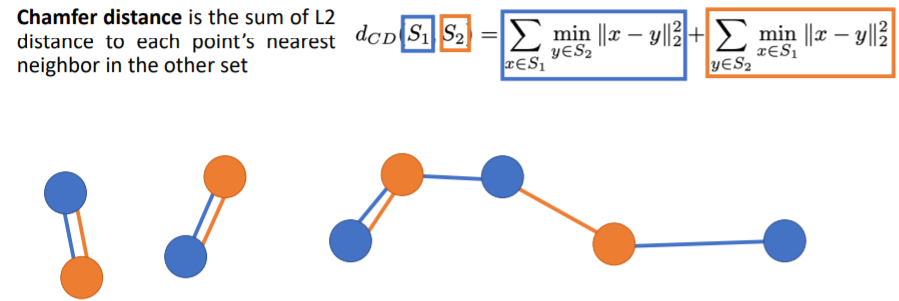두번째 term은 각 orange points에 대해 가장 가까운 blue points를 찾아 둘 사이의 Euclidean distance를 계산하고 이들을 모두 더한다.

그리고 이 두 term을 더해서 최종 Loss값이 나온다.

이 식에서 Loss=0이 되려면 두 pointclouds가 정확히 일치해야한다(coincide perfectly). 각 orange points가 정확히 각 blue points위에 있어야 한다(그 반대도).

2.7) 3D Shape Representations: Triangle Mesh

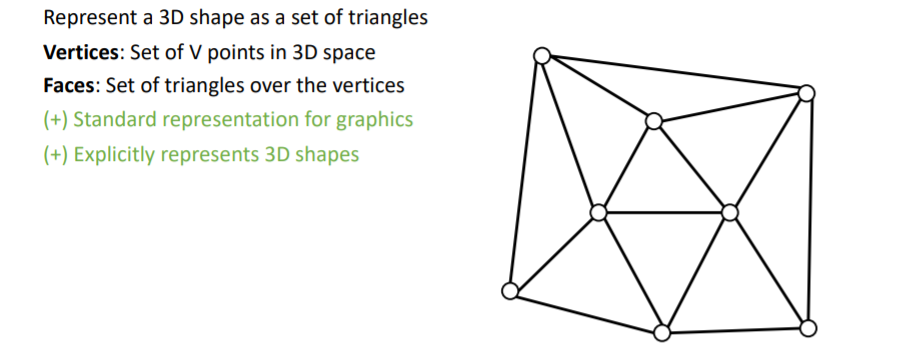3D Triangle Mesh는 컴퓨터그래픽스에서 매우 많이 사용한다. Verticies와 이들로 이루어진 삼각형의 Faces를 사용하여 3d shape를 나타낸다.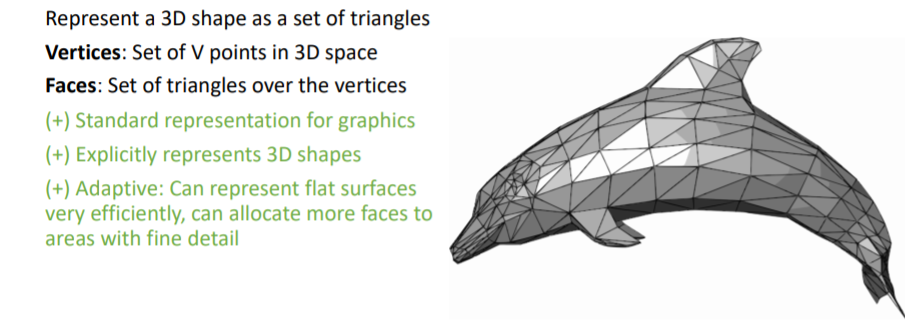평평한 표면을 나타낼 때 효과적이고, 삼각형 Faces의 크기를 조정하여 여러 detail을 표현할 수 있다.또한 각 vertex에 feature이 포함되어있는 경우 coordinate interpolation등을 사용하여 Faces(표면 전체)에 이들 정보를 넣어줄 수도 있는 장점이 있다.

그러나 nerual nets가 수행하기에는 쉽지 않다

2.7.1) Predicting Meshes: Pixel2Mesh

Pixel2Mesh: Generating 3D Mesh Models from Single RGB Images 논문 $\rightarrow$ Nice paper

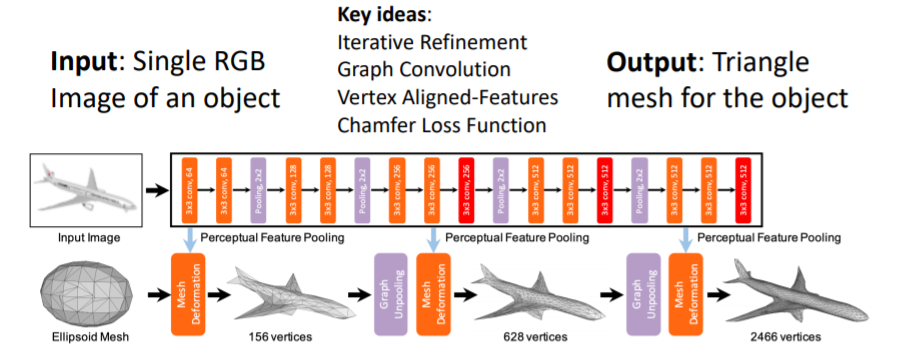single RGB이미지를 input으로 넣어 full 3d shape triangle mesh를 출력한다.

이들은 몇가지의 key ideas를 제시하였다.

Predicting Triangle Meshes: Iterative Refinement (반복적으로 mesh를 미세화.?)

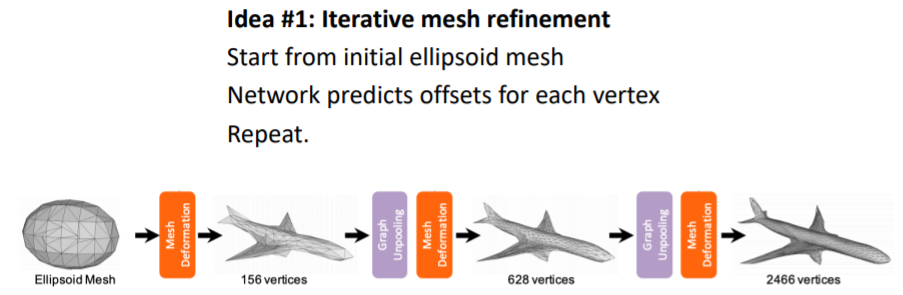처음부터 디테일한 mesh를 얻기는 힘들기 때문에 처음에는 initial template mesh를 가지고 시작한다. 그리고 이를 final mesh output으로 변형한다.
Predicting Triangle Meshes: Graph Convolution

우리는 mesh structured data를 operate할 수 있는 network layer이 필요하다. 이를 위해 Graph Convolution을 사용한다.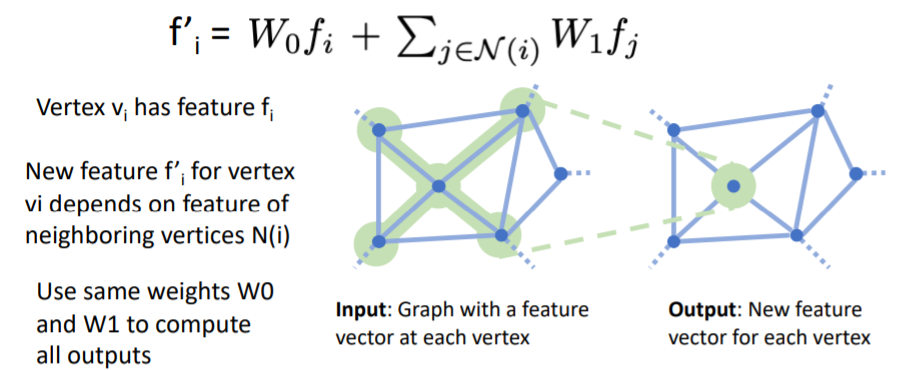Graph Convolution의 Input은 각 vertex에 feature vector이 포함된 Graph이고, Output은 각 vertex에 대해 새로운 feature vector을 계산한다.

이때 각 vertex의 새로운 feature vector은 input graph의 local receptive field의 feature vector에 의존하여 계산된다.
$f'_i=W_0f_i+\sum_{j\in \mathcal N(i)}W_1f_j$
식에서 $v_i$ vertex의 feature $f_i$ 와, $v_i$ 의 neighboring vertices $\mathcal N(i)$ 들의 features $f_j$ 에 대해 weighted sum을 하여 new feature vector $f'_i$ 를 계산한다.

그리고 모든 vertex에 대해서 같은 함수를 적용하여 계산한다.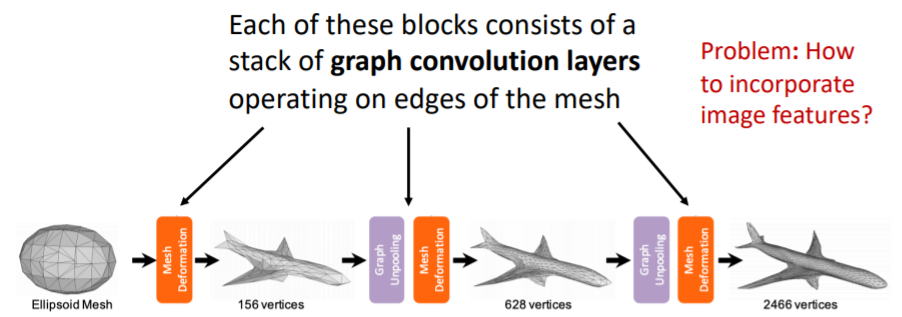네트워크의 각 block들은 위의 여러 층의 graph convolution layers를 포함하고 있으며 이를 통해 coordinate features를 변형한다.

그런데 어떻게 RGB input 이미지와 triangle mesh를 연결지을까?
Predicting Triangle Meshes: Vertex-Aligned Features

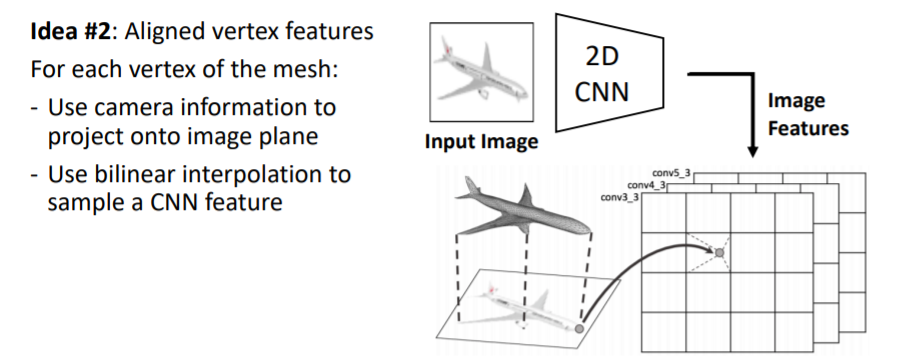mesh의 모든 vertex에 대해 이미지로부터 feature vector(vertex의 위치에 있는 이미지가 어떻게 보이는지에 대한_visual appearance)을 가져온다.

이를 위해 input 이미지를 2d CNN에 넣어 2d feature map을 얻는다.

그리고 mesh의 verticies를 image plane에 projection시킨다(3d $\rightarrow$ 2d projection operator).

2d image plane에 projection된 vertices를 각각 bilinear interpolation을 사용해서 정확한 위치에 대한 image feature vector을 가져온다.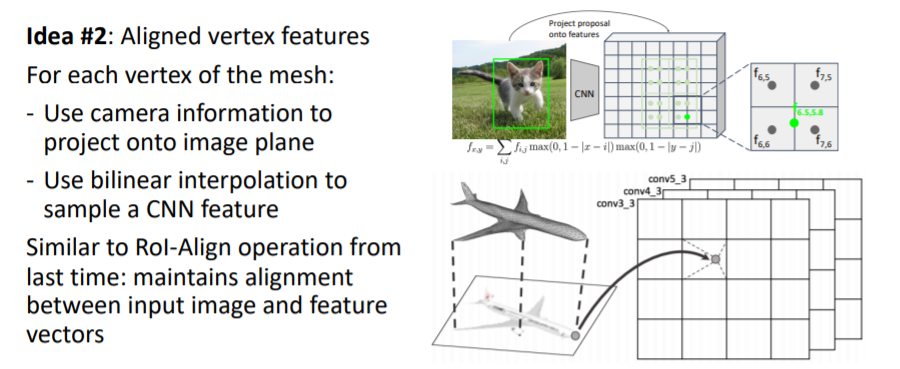
Predicting Meshes: Loss Function

predict한 mesh와 Gt mesh를 비교하는데 한가지 문제점이 있다. 바로 같은 shape를 나타낼 수 있는 방법이 여러가지인 것이다.

예를 들어 사각형을 predict할 때 아래 그림처럼 여러 방법이 존재한다. 그러나 우리는 하나의 shape에 대해 하나의 방법을 원하기 때문에 아래와 같은 방법을 사용하여 비교한다.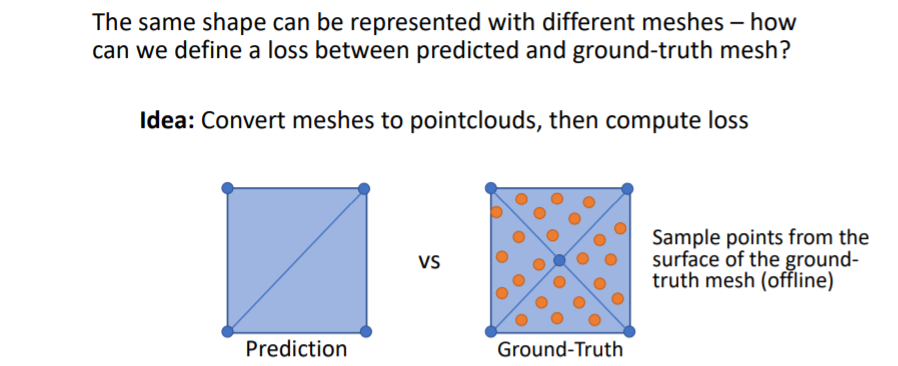mesh에 points를 찍어서 pointcloud로 만든다.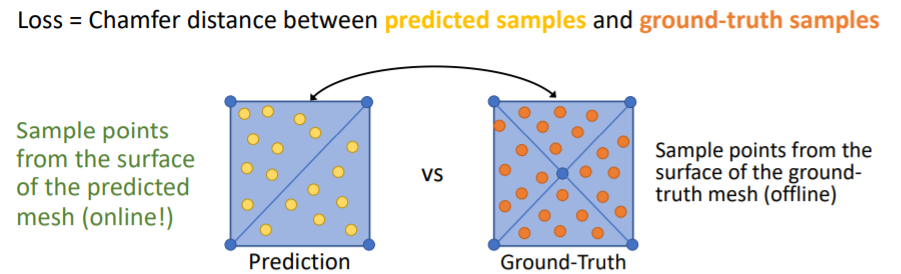그리고 chamfer distance를 사용하여 이 두 point clouds를 비교한다.

그러나 문제가 있다.
1. Need to sample online! Must be efficient!
2. Need to backprop through sampling!
GT mesh는 우리가 학습 이전에 offline에서 point sampling을 해줄 수 있지만 predited mesh의 points는 학습중에 online에서 sampling해야한다. 따라서 이를 효율적으로 빠르게 하는 방법이 필요하고, 이들 points사이의 Loss를 사용하기 때문에 sampling에 따라 backprop이 진행된다.

이 과정에 대한 자세한 내용은 GEOMetrics: Exploiting Geometric Structure for Graph-Encoded Objects 논문에서 확인하라고 한다.

3. Shape Comparison Metrics

이제 3d shapes를 비교하여 성능을 측정하는 방법에 대해 다루어 볼 것이다.

3.1) Shape Comparison Metrics: Intersection over Union

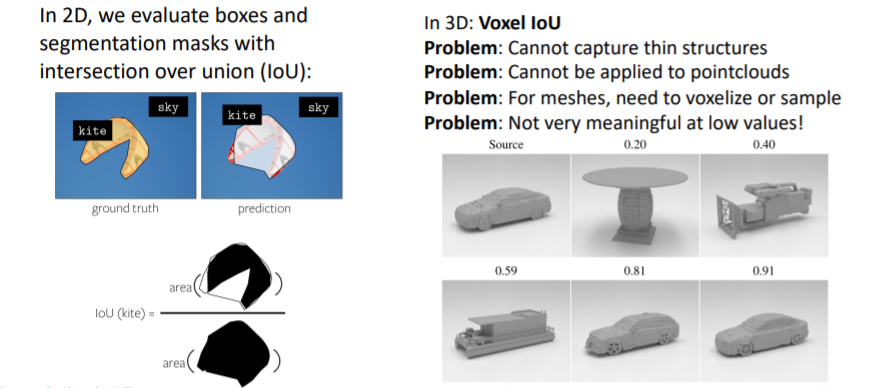우리는 2D이미지를 다룰 때 IoU를 사용하여 성능을 측정하는 방법을 다루었었다. 그러나 3D에서는 IoU는 그다지 의미있거나 유용한 metric은 아니다.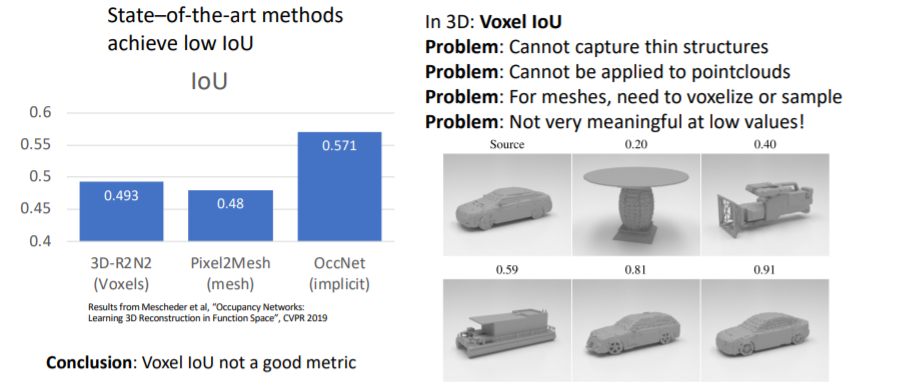

3.2) Shape Comparison Metrics: Chamfer Distance

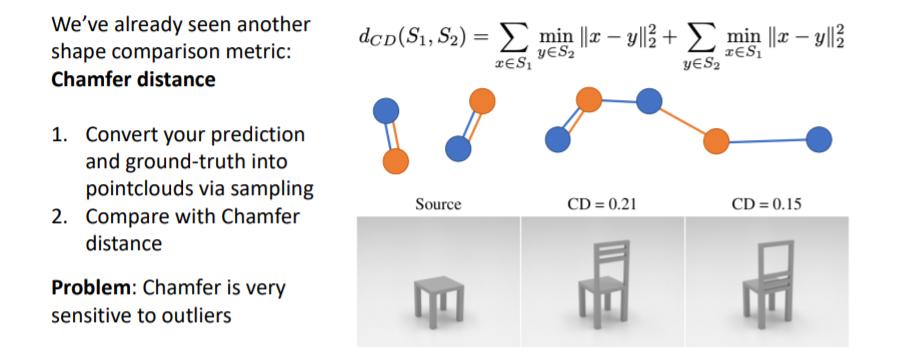이전에 봤던 것처럼 서로 다른 3d shape representations에 points를 sampling하여 point clouds를 만들고 이들을 비교한다.

그러나 L2 distance를 사용하기 때문에 outliers에 매우 sensitive하다.

3.3) Shape Comparison Metrics: F1 Score (Best)

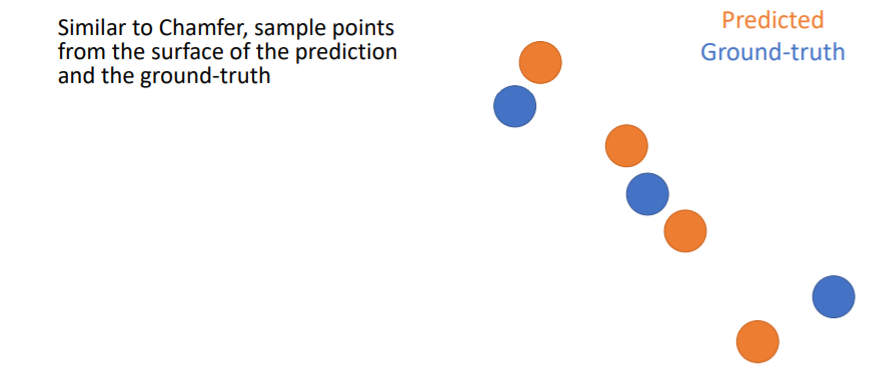Chamfer distance를 계산하는 것과 비슷하게 우선 prediction과 GT에서 points를 sampling한다.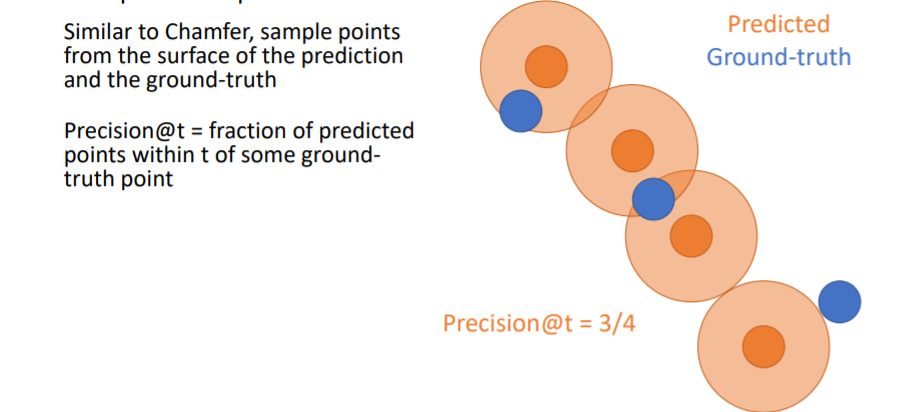그리고 predicted points에 일정 크기의 원을 할당하여 만약 여기 안에 GT point가 들어온다면 그 point는 true predicted point로 설정한다. 위 그림에서는 4개의 predicted points중에 3개의 predicted points가 true이므로 Precision = 3/4 이다.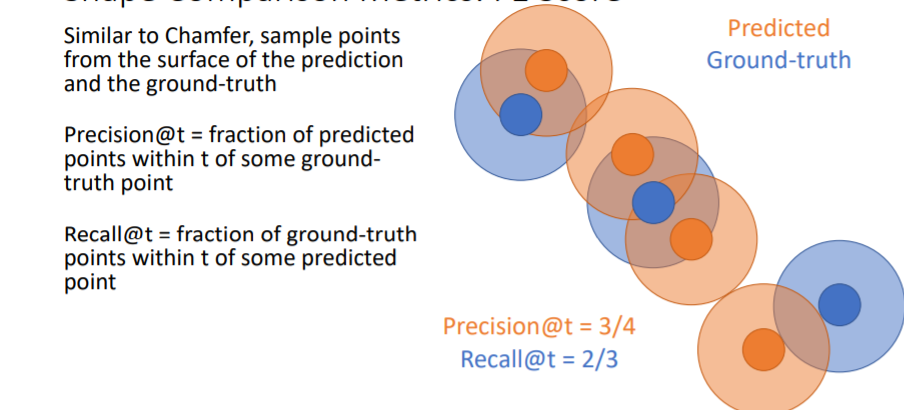Recall은 GT points에 일정 크기의 원을 할당하여 여기 안에 predicted point가 들어오면 true로 한다. 위 그림에서 Recall = 2/3 이다.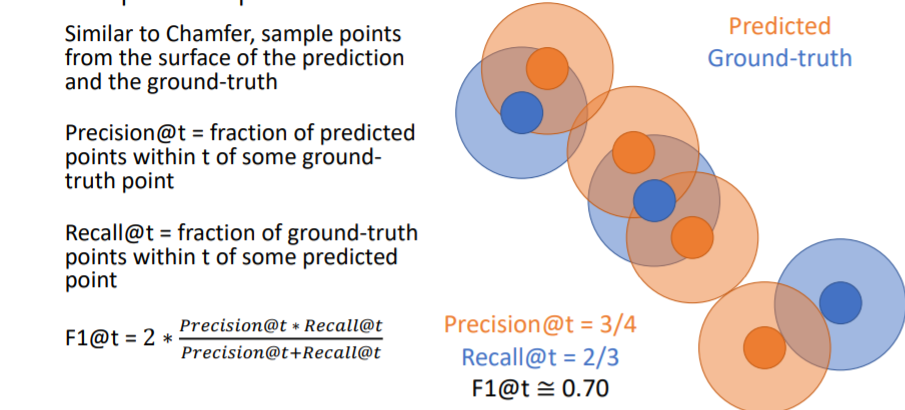위 그림처럼 F1 score을 계산한다.F1 score은 outliers에 robust하기 때문에 가장 좋은 metric이라고 할 수 있다.

3.4) Summary

4. Cameras

3d shapes에 대해 다룰 때는 카메라의 좌표가 매우 중요하다.

4.1) Cameras: Canonical vs View Coordinates

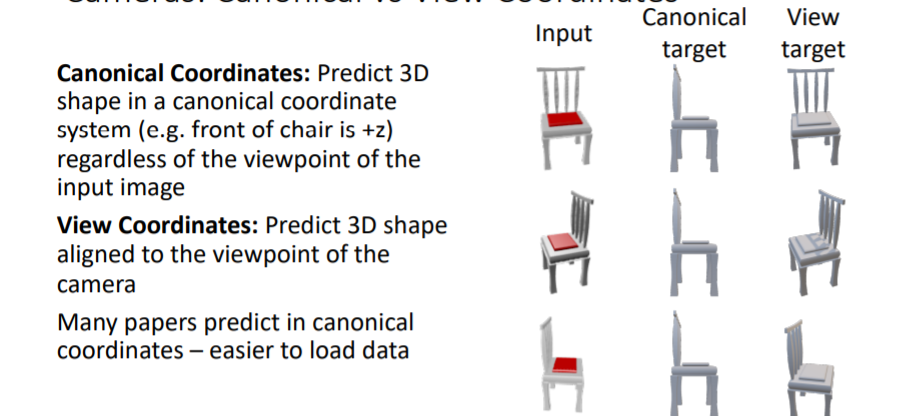
Canonical Coordinates :
표준좌표계로써, left/right/up/down에 대한 방향을 표준화한다. 예를 들어 3d chair을 predict할 때 항상 $+z$ 방향은 의자의 앞부분이고 $+y$ 방향은 항상 의자의 윗부분이며 $+x$ 방향은 의자의 오른쪽부분이다.
View Coordinates :
카메라의 viewpoint를 기준으로 방향이 결정된다.

보통 많은 논문에서는 Canonical Coordinates를 사용한다.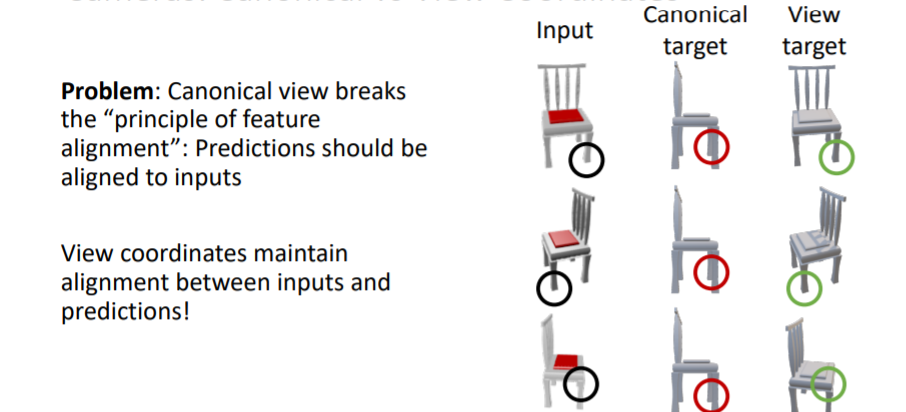그러나 canonical coordinates는 카메라의 viewpoint와 predicted 3d shape의 방향이 서로 align되지 않는 문제가 있다. 대신에 view coordinates는 input과 prediction사이에 view coordinates가 유지된다는 장점이있다.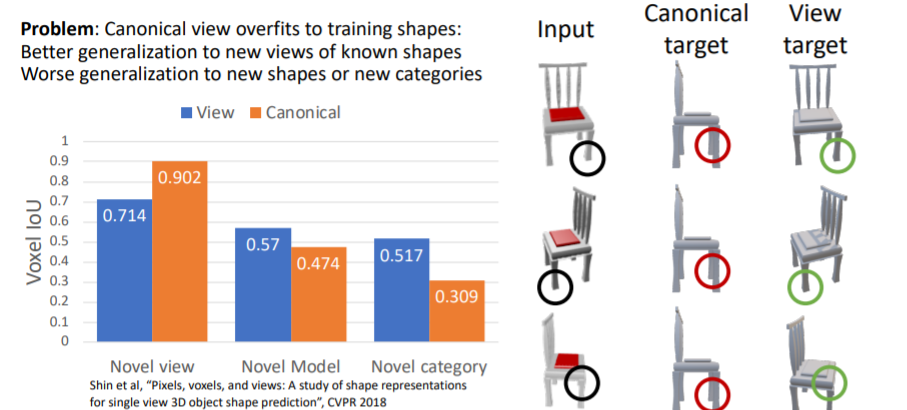실제로 view coordinates를 사용하여 학습시킨 결과가 더 좋은 부분이 있는 것을 확인할 수 있다. 새로운 shape이나 categories에 대해 일반화가 더욱 잘된다.

따라서 view coordinate system을 선호하여 사용하라고 한다.

4.2) View-Centric Voxel Predictions

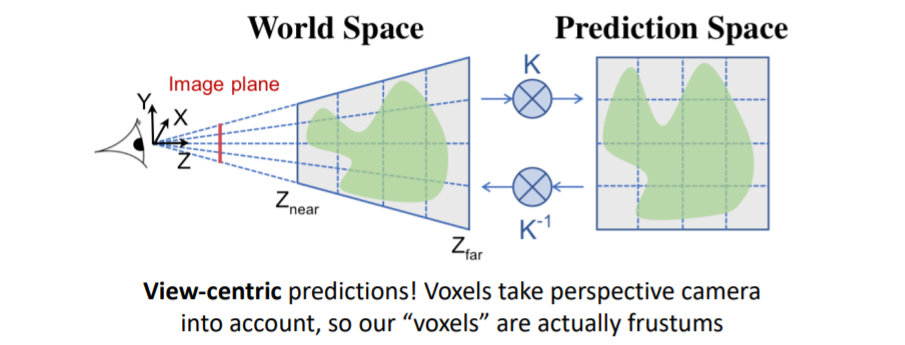음 이건 뭔소린지 잘 모르겠다.

5. 3D Datasets

5.1) 3D Datasets: Object-Centric

6. 3D Shape Prediction: Mesh R-CNN

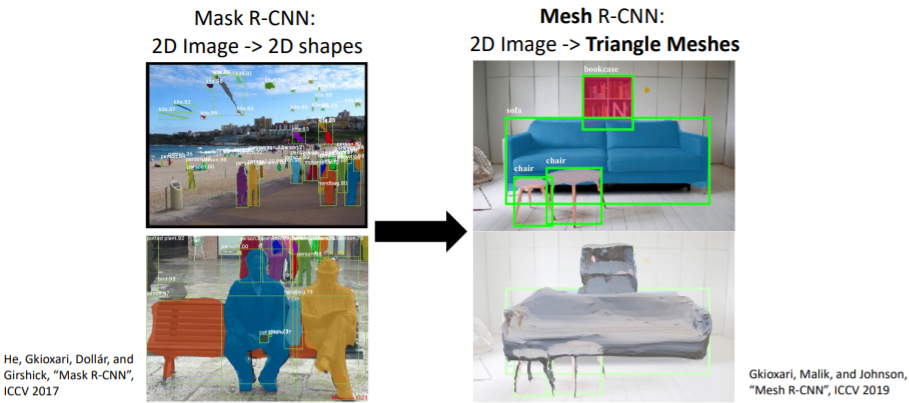지난 시간에 살펴보았던 Mesh R-CNN이다.항상 그래왔듯이 Mask R-CNN을 기반으로 하여 Mesh head를 추가하였다. 여기에서 3D triangle mesh를 output으로 출력한다.

6.1) Mesh R-CNN: Hybrid 3D shape representation

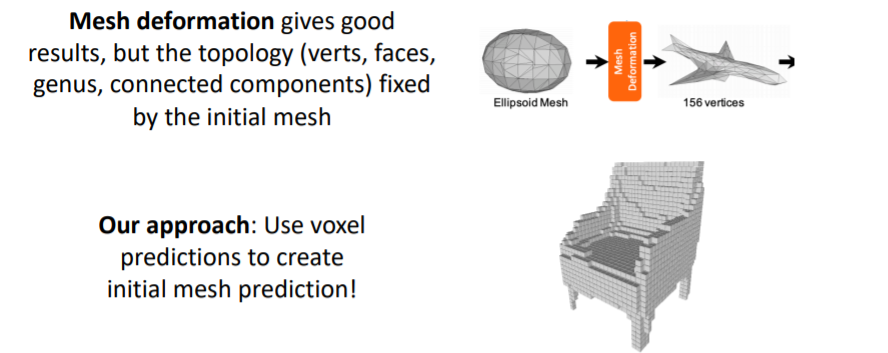Mesh R-CNN에서는 Hybrid 3D shape representation을 사용한다.

앞서 다루었던 triangle mesh의 Mesh deformation은 initial mesh의 topology(위상)에 고정되어있다는 문제가 있다. 예를 들어 sphere로 initialize된 mesh를 사용하면 도넛같은 모양은 아무리 변형해도 만들 수 없다.

따라서 Mesh R-CNN에서는 coarse voxel prediction을 먼저 만들고, 이를 mesh로 convert시켜준다. 그리고 이를 initial mesh로 사용한다.

6.2) Mesh R-CNN Pipeline

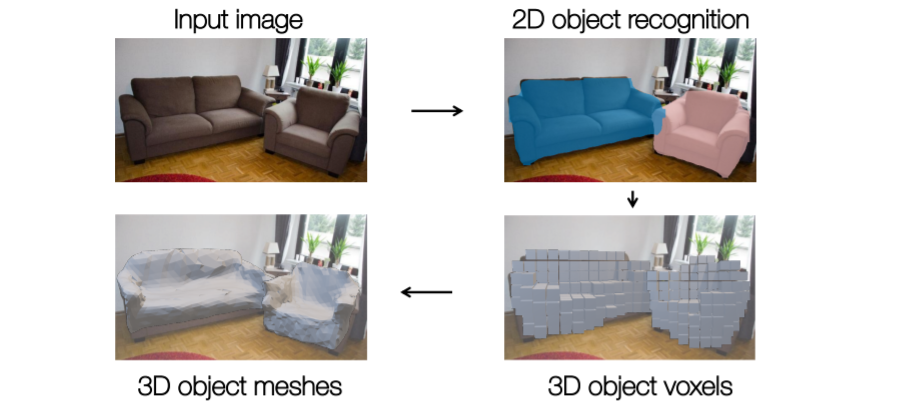
1.2D object recognition까지는 기존 mask R-CNN과 동일하다(RPN을 사용한다던지 등..).
2. 그런데 이제 여기에서 voxel tube network를 사용하여 coarse voxel prediction을 진행한다.
3. 그리고 이를 blocky mesh representation으로 convert시키고 initial mesh로 사용한다.
4. 최종적으로 3d object meshes를 출력한다.

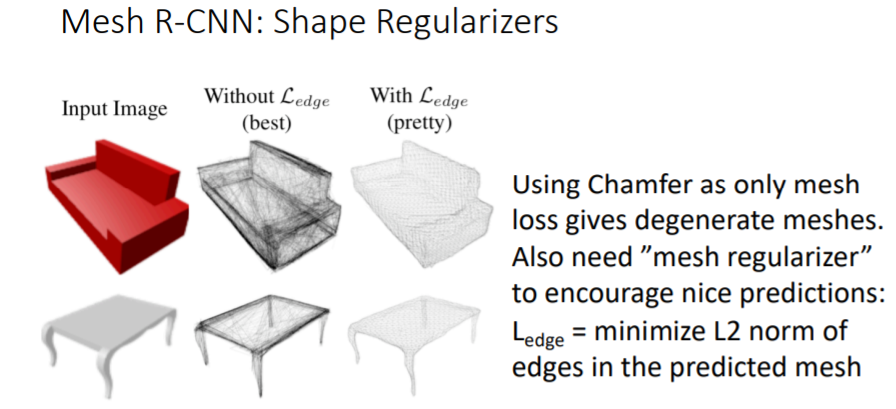그리고 Chamfer Loss만 사용하지 않고 mesh regularizer을 추가로 사용하여 더 좋은 prediction결과를 얻었다.

6.3) Mesh R-CNN Results

sphere로 initial mesh를 주는 Pixel2Mesh와 비교해보면 이미지의 물체에 있는 구멍을 잘 표현하는 것을 볼 수 있다. sphere로 initialize된 mesh는 위상적으로 구멍을 만들어낼 수 없다.물체의 보이지 않는 뒷부분까지 mesh로 출력할 수 있다.object detection으로 많은 objects를 predict할 수 있지만 완벽하지는 않다.Amodal completion이라는 특징을 갖는다. 위 그림처럼 개에게 가려진 소파이지만 가려진 부분도 predict가 가능하다.그러나 위 그림에서 segmentation fail이 mesh prediction fail로 이어지는 것처럼 2D recognition fails가 3d recognition fails를 불러온다.