2024/12/24 화 매일 백준

오늘의 문제는,

1149번: RGB거리

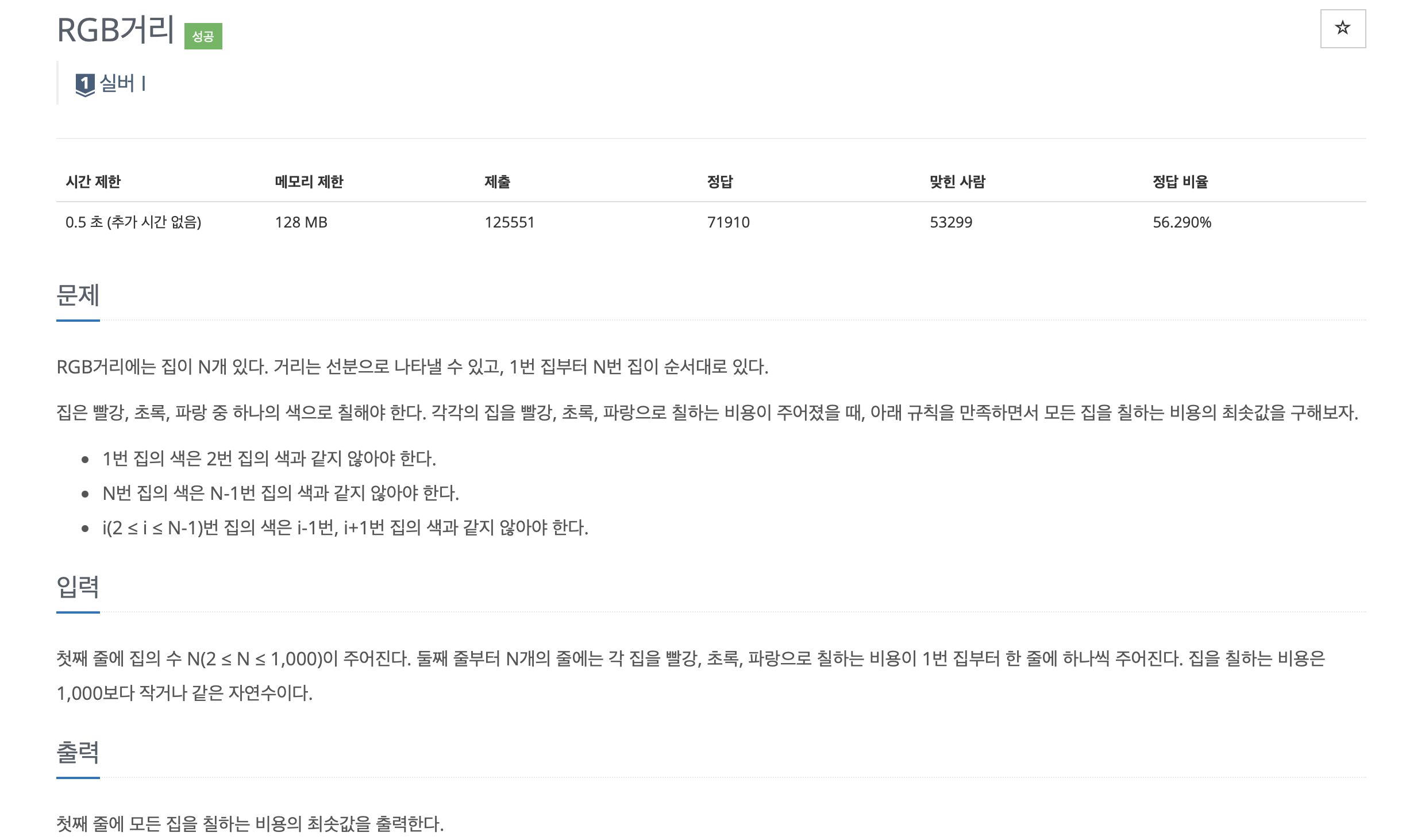
즉, 겹치지 않게 색칠할 수 있는 최소 비용을 구하라 ~ 문제이다.

단순히 최소 비용을 선택해서 나아간다해서 해결되는 문제가 아니다.
이전의 선택의 이후의 선택에 영향을 주기 때문에
이전 선택하는 색의 R,G,B인 경우를 고려하여서 구하며 된다.

#include <iostream>
#include <algorithm>

using namespace std;

int main(void) {

    int N = 0, home[1001][3], DP[1001][3];

    cin >> N;

    for(int i=1;i<=N;i++) {
        cin >> home[i][0] >> home[i][1] >> home[i][2];
    }

    for(int i=1;i<=N;i++) {
        DP[i][0] = min(DP[i - 1][1], DP[i - 1][2]) + home[i][0];
        DP[i][1] = min(DP[i - 1][0], DP[i - 1][2]) + home[i][1];
        DP[i][2] = min(DP[i - 1][0], DP[i - 1][1]) + home[i][2];
    }

    int result = min(DP[N][0], DP[N][1]);
    result = min(DP[N][2], result);

    cout << result << endl;

    return 0;
}

그래서 각 경우에 맞게 최소값을 구하여서 최종적으로 가장 적은 비용을 출력하면 되는 문제.

내일은 크리스마스니 ,,, 그냥 하루 쉬련다. PS말고도 따로 앱 개발을 해보려고 준비 중인데 그거랑 다른 일 좀 하도록 하겠음

끝.