2024/12/23 월 매일 백준

오늘의 문제는

2579: 계단 오르기

이다

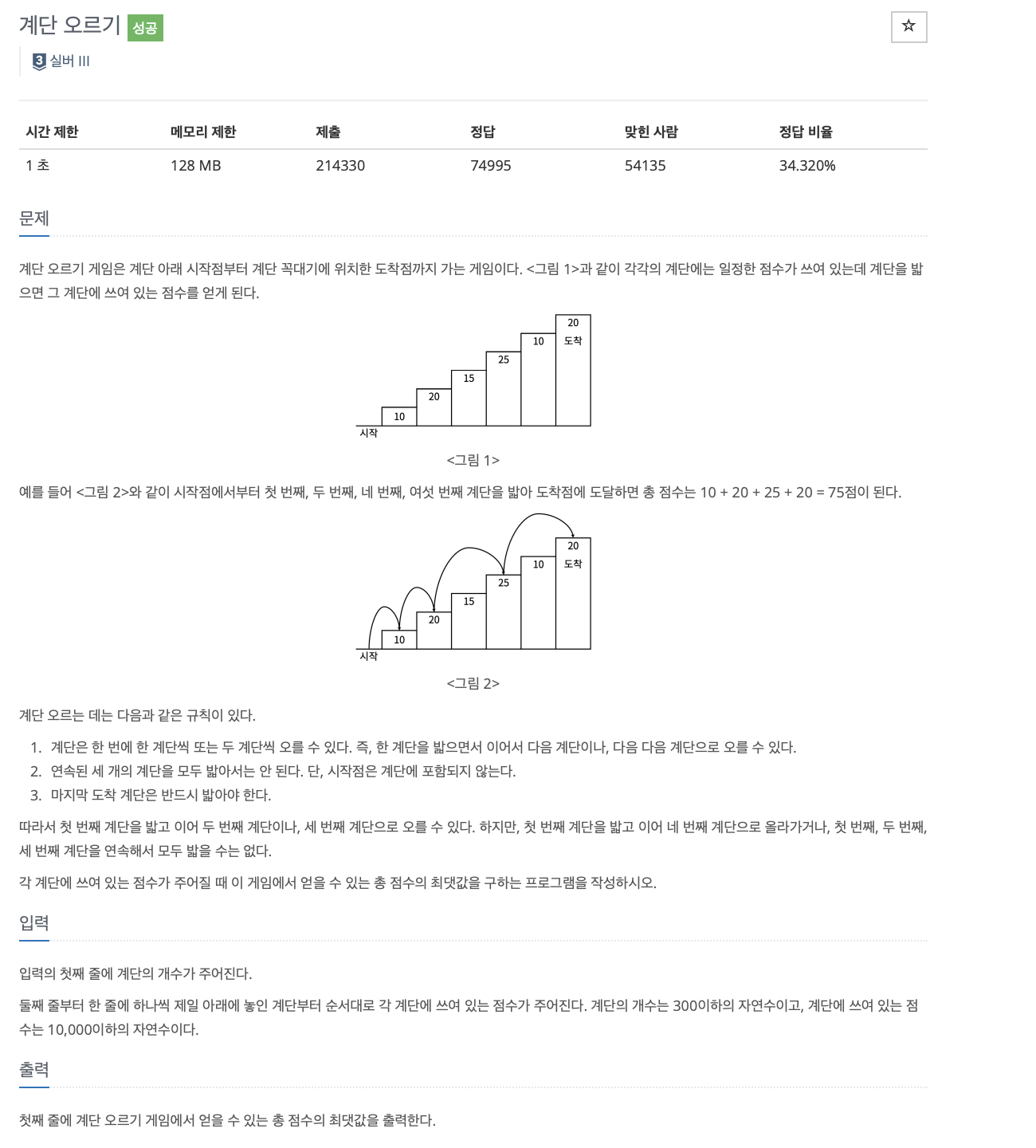
문제는 다음과 같고,
규칙을 지키면서 가장 높은 점수의 계단 오르기를 수행하면 된다.

DP라 하면은 작은 문제가 큰 문제에 해결되어야한다를 뭔가 이제서야 깨닫게해준 것 같다.
그 동안은 그냥 본능적으로 앞의 값 가져와서 풀면 되겠네 ~ 라는 생각을 가지고 풀었다면은

이 단계를 거치기 위해서는 전 단계에는 어떻게 계단을 올라야할까에 대해서 좀 생각을 해보게되었다. 남들에게는 쉽고 간단한 문제일지라도 나한테 있어서 굉장히 의미가 큰 문제였다

바로 풀이로 가보도록 하겠다.

지금까지 문제를 풀 때에는 작은 문제부터 시작해서 큰 문제로 도달하는 과정을 떠올린 뒤에 알고리즘을 생각했는데, 이 문제는 세 번째 규칙인 "마지막 도착 계단은 반드시 밟아야 한다."를 통하여 큰 문제에서 작은 문제로 도달하는 생각의 흐름을 거쳤다.

흐름은 아래와 같다.

마지막 N번째 계단을 밟기위해서는 두 개의 경우의 수가 존재한다.
1. N-3 -> N-1 -> N
2. N-2 -> N
위 순서로 계단을 밟을 수 있다.
둘 중 더 큰 값을 고르면 해결되는 문제이다.

#include <iostream>
#include <algorithm>

using namespace std;

int main(void) {

    int n = 0;
    cin >> n;

    int DP[n + 1], stairs[n + 1];
    for(int i=1;i<=n;i++) {
        cin >> stairs[i];
    }

    DP[1] = stairs[1];
    DP[2] = stairs[1] + stairs[2];
    DP[3] = max(stairs[1], stairs[2]) + stairs[3];

    for(int i=4;i<n+1;i++) {
        DP[i] = max(DP[i - 2], DP[i - 3] + stairs[i - 1]) + stairs[i];
    }

    cout << DP[n] << endl;

    return 0;
}

풀어보기 잘한 것 같다.