[Data Processing] NumPy 심화

🔣 기본 연산

◽ 사칙연산

• np.add() : 덧셈
• np.subtract() : 뺄셈
• np.multiply() : 곱셈
• np.divide() : 나눗셈

◽ np.sum() 또는 ndarray.sum()

• 배열의 합 반환

2차원에서의 sum

arr = np.array([
    [1, 2, 3], 
    [4, 5, 6]
])
print(arr)
print(arr.shape)

[[1 2 3]
 [4 5 6]]
 
(2, 3)  # 2행 3열

• axis = None : 배열의 모든 원소의 합

  np.sum(arr, axis=None)	# 21

• axis = 0 : 행 압축 → 열 안의 원소끼리 더함

  np.sum(arr, axis=0)	# [5 7 9]

• axis = 1 : 열 압축 → 행 안의 원소끼리 더함

  np.sum(arr, axis=1)	# [ 6 15]

3차원에서의 sum

arr = np.array([
    [[1, 2, 3], 
     [4, 5, 6]],
    [[10, 20, 30],
     [40, 50, 60]]
])
print(arr)
print(arr.shape)

[[[ 1  2  3]
  [ 4  5  6]]

 [[10 20 30]
  [40 50 60]]]
  
(2, 2, 3)  
# 2깊이 2행 3열
# 2개의 2행 3열

• axis = None : 배열의 모든 원소의 합

  np.sum(arr, axis=None)	# 231

• axis = 0 : 차원 압축 → 같은 자리의 원소끼리 더함

  np.sum(arr, axis=0)
  # [[11 22 33]
  #  [44 55 66]]

• axis = 1 : 각 차원의 행 압축 → 열 안의 원소끼리 더함

  np.sum(arr, axis=0)
  # [[ 5  7  9]
  #  [50 70 90]]

• axis = 2 : 열 압축 → 행 안의 원소끼리 더함

  np.sum(arr, axis=1)
  # [[  6  15]
  #  [ 60 150]]

◽ np.min() 또는 ndarray.min()

• 배열의 최솟값 반환

arr = np.array([
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]
])

• axis = None : 전체 배열 내의 최솟값

  np.min(arr, axis=None)		# 1

• axis = 0 : 최솟값을 갖는 행

  np.min(arr, axis=0)		# [1 2 3]

• axis = 1 : 최솟값을 갖는 열

  np.min(arr, axis=1)		# [1 4 7]

◽ np.max() 또는 ndarray.max()

• 배열의 최솟값 반환

arr = np.array([
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]
])

• axis = None : 전체 배열 내의 최댓값

  np.max(arr, axis=None)		# 9

• axis = 0 : 최댓값을 갖는 행

  np.max(arr, axis=0)		# [7 8 9]

• axis = 1 : 최댓값을 갖는 열

  np.max(arr, axis=1)		# [3 6 9]

---

🤯 선형대수 (벡터/행렬 연산) 함수

◽ Norm

• 벡터의 크기
  

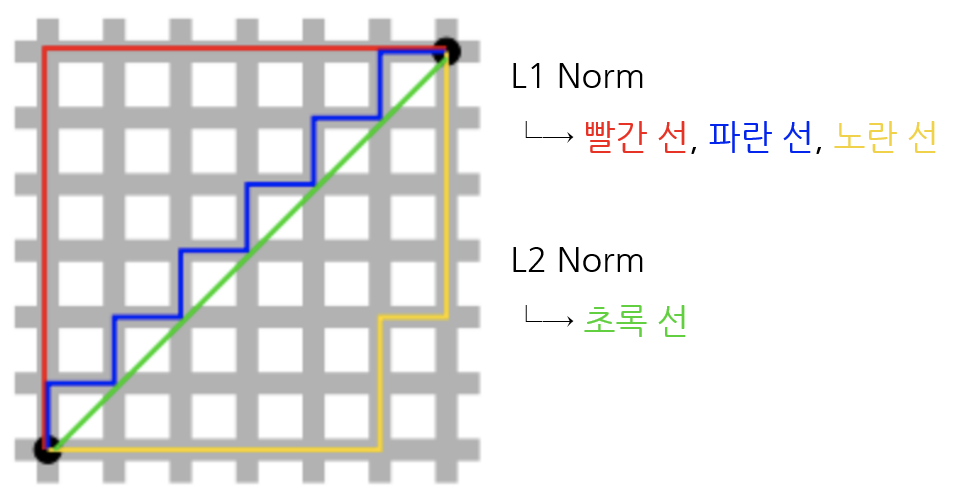
L1 Norm (Manhattan Distance)

• 두 개의 벡터를 빼고, 절댓값을 취한 뒤 합한 것
• $x = [1, 2, 3, 4, 5]$ 일 때,
  $L1 = (|1| + |2| + |3| + |4| + |5|) = 15$

L2 Norm (Euclidean Distance)

• 두 개의 벡터의 각 원소를 뺴고, 제곱을 하고, 합치고, 루트를 씌운 것
• $x = [1, 2, 3, 4, 5]$ 일 때
  $L2 = \sqrt{(|1|^2 + |2|^2 + |3|^2 + |4|^2 + |5|^2)}$

◽ L1 Norm과 L2 Norm의 차이점

	L1 Norm	L2 Norm
벡터 간 거리 구하는 방법	절댓값	제곱값
특징	outlier에 둔감함	outlier에 민감함

◽ Norm의 필요성

• Regularization (일반화)
  • 모델의 파라미터에 제약을 주어 모델의 복잡도를 낮춤
  • 과적합을 방지하기 위한 방법 중 하나
• Regularization을 하기 위해 필요한 개념이 norm
• 나중에 봐야즹
  • 참고자료 1
  • 참고자료 2
  • 참고자료 3

◽ NumPy에서의 Norm

linalg : linear algebra

u = np.array([1, 2, 3, 4, 5])

L1 Norm

np.linalg.norm(u, 1)
# 15.0

L2 Norm

np.linalg.norm(u)
np.linalg.norm(u, 2)
# 7.416198487095663

---

✖ 벡터 내적

• 두 벡터의 각 요소 간 곱의 합 (결과는 스칼라값)
• 두 개의 벡터가 서로 유사할수록 내적 값이 큼
  → 닮음 정도를 평가할 때 가장 유용하게 쓰이는 수학적 도구

◽ np.dot() 또는 @ 연산자

• 1차원 배열의 내적

x = np.array([1, 2, 3])
y = np.array([4, 5, 6])

print('내적 :', x @ y)
print('내적 :', np.dot(x, y))
print('x 내적 y의 전치행렬 :', x.dot(y.T))
print('y 내적 x의 전치행렬 :', y.dot(x.T))
# 32

• 2차원 배열의 내적

x = np.array([[1], [2], [3]])
y = np.array([[4], [5], [6]])

print('shape :', x.shape)	# (3, 1)
print('shape :', y.shape)	# (3, 1)
# print(x @ y) → 오류
print(x.T @ y)
# array([[32]])

---

🔀 역행렬

• 역행렬의 의미
• 행렬 $A$ · 역행렬 $A^-$$^1$ = 단위행렬
• 나눗셈 같은 개념

◽ np.linalg.inv()

x = np.array([
    [1, 2, 3],
    [1, 0, 0],
    [0, 0, 1]
])
y = np.linalg.inv(x)

print(x)
print('-' * 20)
print(y)
print('-' * 20)
print(x @ y)

[[1 2 3]
 [1 0 0]
 [0 0 1]]
--------------------
[[ 0.   1.   0. ]
 [ 0.5 -0.5 -1.5]
 [ 0.   0.   1. ]]
--------------------
[[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]

---

💫 난수 (random)

◽ rand()

• [0, 1) 사이의 난수 배열 생성
• np.random.rand(1000)

◽ randint()

• [최솟값, 최댓값) 사이의 임의의 정수 배열 생성
• np.random.randint(0, 10, 1000)

◽ randn()

• 표준정규분포로부터 샘플링된 난수 배열 생성
• np.random.randn(1000)
  • 평균 0, 표준편차 1인 정규분포 (= 표준정규분포 N(0, 1))
• 3 * np.random.randn(1000) + 2
  • 평균 2, 표준편차 3인 정규분포 (N(2, 3²))

◽ standard_normal()

• randn과 똑같음
• np.random.standard_normal(1000)

◽ normal()

• 정규분포로부터 샘플링된 난수 배열
• np.random.normal(0, 1, 1000)
  • 평균 0, 표준편차 1인 정규분포 (= 표준정규분포 N(0, 1))
• np.random.normal(1.5, 1.5, 1000)
  • 평균 1.5, 표준편차 1.5인 정규분포 (N(1.5, 1.5²))

◽ random_sample()

• [0, 1) 범위에서 샘플링된 임의의 실수 배열 생성
• np.random.random_sample(1000)
• [a, b) 범위로 바꾸고 싶으면 (b - a) * random_sample(1000) + a
• 2 * np.random.random_sample(1000) -1

◽ choice()

• 1차원 배열로부터 임의의 샘플 배열 생성
• np.random.choice(10, 1000)
  • np.arange(10)에서 난수 1000개 생성
• np.random.choice([0, 1, 2, 3, 4], 1000)
  • [0, 1, 2, 3, 4]에서 난수 1000개 생성