[Python] Python TMI

🤷🏻‍♀️ 실수 표현 시 왜 오차가 발생하는가?

• 컴퓨터는 2진 데이터로 이루어져 있기 때문에 소수점을 정확히 표현할 수 없음
• 최대한 따라하기 위해 '부동소수점'을 사용하여 10진수의 근삿값을 실수(float)로 표현

print(0.1 * 3 == 0.3)	# False
print(0.1 * 3)			# 0.30000000000000004

🙆🏻‍♀️ 해결책

decimal.Decimal 사용

from decimal import Decimal

dec = Decimal('0.1') * 3
print(dec == Decimal('0.3'))	# True
print(dec)						# 0.3

math.isclose 사용

from math import isclose

print(isclose(0.1*3, 0.3))	# True

---

🤷🏻‍♀️ 인수와 인자의 차이는 무엇인가?

def add(a, b):
	return a + b

five = 5
six = 6
total = add(five, six)

🙆🏻‍♀️ 인자 / 매개변수 / parameter

• 함수를 정의할 때 사용하는 변수
• a, b

🙆🏻‍♀️ 인수 / argument

• 함수를 호출할 때 사용하는 변수
• five, six

---

🤷🏻‍♀️ pickle 사용법

• pickle은 텍스트 상태의 데이터가 아닌 파이썬 객체 자체를 파일로 저장

🙆🏻‍♀️ pickle 저장하기

import pickle

info = {'a': 1, 'b': 2, 'c': 3}

with open('info.pkl', 'wb') as f:
	pickle.dump(info, f)

🙆🏻‍♀️ pickle 불러오기

import pickle

with open('info.pkl', 'rb') as f:
	info = pickle.load(f)

---

🤷🏻‍♀️ 몬티 홀 문제

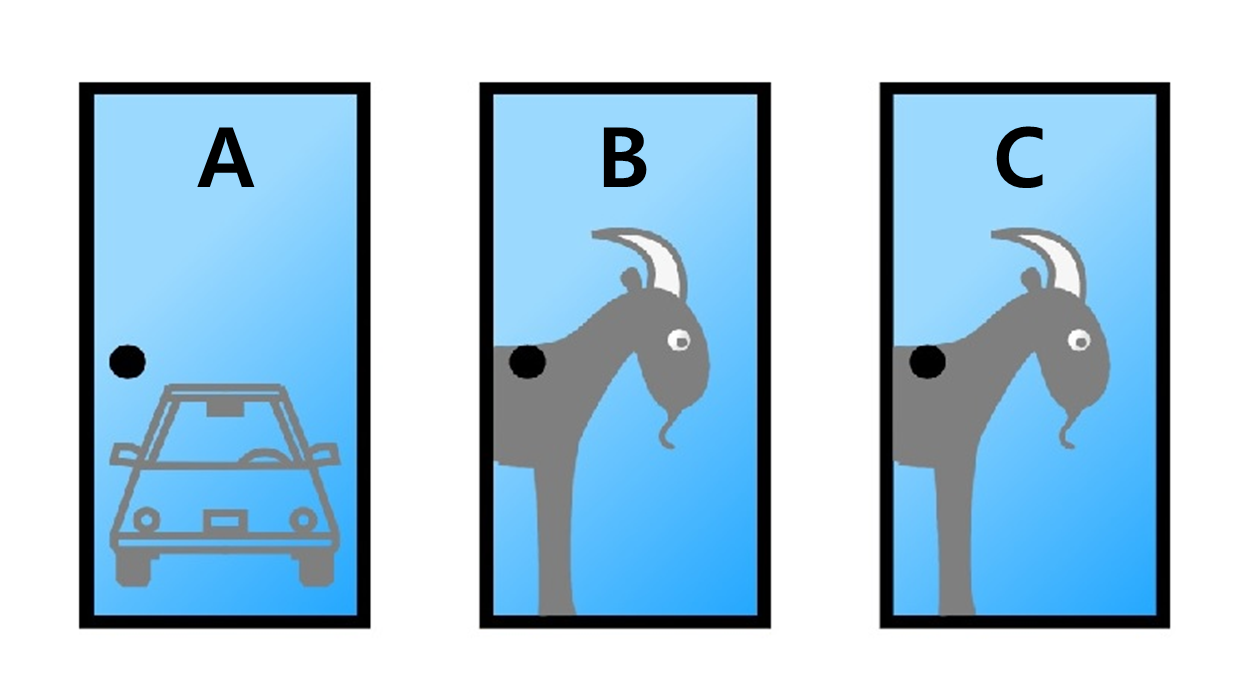
• 문 세 개가 있음
• 하나의 문 뒤에는 새 차 (당첨), 나머지 둘은 염소 (꽝)
• 당신이 A를 골랐다고 하면, 출제자는 고르지 않은 문 두 개 (B, C) 중 꽝인 문(C)을 엶
• 열린 문(C)을 제외하고 나머지 두 개(A, B)의 문 중 답을 다시 골라보라고 함
• 당신은 답을 유지할 것인가요 답을 바꾸실건가요?

🙆🏻‍♀️ 해결책

하나의 경우(A가 당첨일 경우)만 생각해보도록 하자

🙆🏻‍♀️ 코딩

한 번 실행해 보기

import random

doors = ['A', 'B', 'C']

# 당첨인 문을 랜덤으로 하나 정하기
prize = random.sample(doors, 1)[0]
print(f'당첨인 문 : {prize}')

# 답 선택하기
pick = random.sample(doors, 1)[0]
print(f'내가 선택한 문 : {pick}')

# 당첨 문과 선택한 문의 집합
tmp_set = {prize, pick}

# 당첨 문과 선택한 문을 제외한 문 열기
remain = list(set(doors) - tmp_set)
open_door = random.sample(remain, 1)[0]
print(f'진행자가 연 문 : {open_door}')

# 답 바꿀 경우 최종적으로 선택하게 되는 문
# 문 중에서 진행자가 연 문과 내가 고른 문을 제외한 나머지 문
switch = list(set(doors) - set(open_door) - set(pick))[0]
print(f'바꾼 답 : {switch}')

win_without_switch = []
win_with_switch = []

# 답을 유지하고 당첨되었을 경우
if pick == prize:
    win_without_switch.append(1)

# 답을 바꾸고 당첨되었을 경우
if switch == prize:
    win_with_switch.append(1)

print(f'답 유지하고 당첨 : {win_without_switch}')
print(f'답 바꾸고 당첨 : {win_with_switch}')

당첨인 문 : B
내가 선택한 문 : A
진행자가 연 문 : C
바꾼 답 : B
답 유지하고 당첨 : []
답 바꾸고 당첨 : [1]

시뮬레이션

win_without_switch = []
win_with_switch = []
doors = ['A', 'B', 'C']

for x in range(1_000_000):
    # 당첨인 문 & 내가 선택한 문
    prize = random.sample(doors, 1)[0]
    pick = random.sample(doors, 1)[0]

    tmp_set = {prize, pick}
    remain = list(set(doors) - tmp_set)
    open_door = random.sample(remain, 1)[0]

    switch = list(set(doors) - set(open_door) - set(pick))[0]

    # 답을 유지하고 당첨되었을 경우
    if pick == prize:
        win_without_switch.append(1)

    # 답을 바꾸고 당첨되었을 경우
    if switch == prize:
        win_with_switch.append(1)

print(f'답 유지하고 당첨될 확률 : {len(win_without_switch)} / 1,000,000')
print(f'답 바꾸고 당첨될 확률 : {len(win_with_switch)} / 1,000,000')  

답 유지하고 당첨될 확률 : 333626 / 1,000,000
답 바꾸고 당첨될 확률 : 666374 / 1,000,000

---

💁🏻‍♀️ 찐 TMI

• j : 파이썬에서의 허수 표현

  >> 3j + 9j 	# 12j