CS231N, EECS 498-007 / 598-005에서 나타나는 개념을 정리하기 위하여 복기용도로 작성하였습니다.
간단히 정리한 내용을 살펴보며 모르는 부분이 있을 때 찾아보는 용도로 보시면 좋을 것 같습니다.
optimization
- loss function은 특정한 weights 집합 의 quality를 정량화화여 나타냅니다.
- optimization의 목표는 loss function을 최소화 하는 를 찾는 것입니다.
gradient
- 1차원 함수의 경우, 어떤 점에서 움직일 때 slope(기울기)는 함수값의 순간 증가율을 나타낸다.
- gradient는 변수가 single number가 아니라 vector of numbers인 경우로, slope를 일반화시킨 것이다.
- gradient는 input space의 각 dimension에 해당하는 slopes (derivatives, 대게 미분이라 불림)들의 백터이다.
- 1차원 함수의 derivative를 수식으로 쓰면 다음과 같다.
- functions이 a vector of numbers를 입력을 받는 경우, the derivatives(미분)을 partial derivatives(편미분)이라고 하며, the gradient는 각 dimension의 partial derivatives를 모은 벡터이다.
- numerical gradient 계산방법
- h가 0으로 수렴할 때의 극한값이 gradient의 수학적으로 정의인데, (예시 1e-5) 작은 값이면 충분하다
- 업데이트할 때, gradient df의 negative direction으로 움직인 것을 주목하자. 왜냐하면 우리가 원하는 것은 loss function의 증가가 아니라 감소하는 것이기 때문이다.
- 계산 시간은 O(#dimesions)으로 느리고, gradient가 정확한 값이 아닌 근사값이다.
- step size(learning rate)선택은 neural network학습에서 가장 중요한 hyperparameter 설정이다. 너무 작다면 수렴속도가 길어지며, 크다면 수렴범위를 벗어날 수 있다.
- analytic gradient 계산방법
- numerical gradient에 비하여 계산하기 매우 빠르지만 구현할 때 실수 하기 쉽다. 따라서 analytic gradient으로 구한 다음 numerical gradient으로 비교하며 고치는 과정수행하며, 이를 gradient check라고 한다.
- SVM loss function for a single datapoint:
- taking the gradient with respect to we obtain:
- 는 indicator function으로 내부 조건이 참이면 1, 아니면 0이다.
- 위식은 참인 클래스에 해당하는 의 행으로 미분했을 때의 gradient는이다. 인 다른 행에 대한 gradient는 다음과 같다.
Gradient Descent
- 반복적으로 gradient를 평가하고 parameter update를 수행하는 것을 Gradient Descent라고 한다. vanilla version은 아래와 같다:
# Vanilla Gradient Descent
while True:
weights_grad = evaluate_gradient(loss_fun, data, weights)
weights += - step_size * weights_grad # perform parameter update- Huperparameters
- Weight initialization method
- 초기값 위치에 따라 수렴 위치&속도가 달라진다.
- Number of steps
- steps수가 크면 수행시간이 오래걸리며, 작으면 수렴하기전에 끝날 수 있다.
- Learning rate
- 크게 설정하면 optimal 값에 도달하지않고 지나칠 수 있으며, 작으면 시간이 오래 걸린다.
- Weight initialization method
- Mini-batch gradient descent
- training data가 수백만개 주어질 수 있다. 따라서, 파라미터를 한 번 업데이트하려고 entire training set 전체를 계산에 사용하는 것은 낭비가 될 수 있다.
- 이를 극복하기 위해서 training data의 batches만 이용해서 gradient를 구하는 것이다
- the training data가 correlated되어 있음에 적용가능하다.
# Vanilla Minibatch Gradient Descent
while True:
data_batch = sample_training_data(data, 256) # 예제 256개짜리 미니배치(mini-batch)
weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
weights += - step_size * weights_grad # 파라미터 업데이트(parameter update)- Stochastic Gradient Descent (SGD)
- SGD가 엄밀한 의미에서는 single example인 mini-batch에서 gradient를 계산하는 것이지만, 많은 사람들이 그냥 MGD(Minibatch Gradient Descent)를 의미하면서 SGD라고 부르기도 한다
- mini-batch의 크기도 hyperparameter이지만, 이것을 cross-validate하는 일은 흔치 않다. 이건 대체로 컴퓨터 메모리 크기의 한계에 따라 결정되거나, 몇몇 특정값 (예를 들어, 32, 64 or 128)을 이용한다. 2의 제곱수를 이용하는 이유는 많은 벡터 계산이 2의 제곱수가 입력될 때 더 빠르기 때문이다.
강의내 질의 응답
-
SGD의 문제점1
Q: What if loss chages quickly in one diretion and slowly in another?
Q: What does gradient descent do?
A: shallow dimension에서 천천히 이동하며 깊은 방향으로 이동할 때 지그재그형태로 움직인다.
-
SGD의 문제점2
Q: What if the loss function has a local minimum or saddle point?
A: Local minimum과 saddle point에서의 gradient값은 0이 되며 weight 업데이트 못한다.
-
SGD의 문제점3
gradient가 minibatches에서 계산하므로 noise가 있다.
SGD+Momentum
- Build up “velocity” as a running mean of gradients
- Rho gives “friction”; typically rho=0.9 or 0.99
- 공식에따라 다르게 나타날 수 있지만 중간 그림과 오른쪽 그림은 동등한 식이다.
- local minima, Saddle points에서도 이전에 내려오던 속도가 있어 지날 수 있다.
- 속도가 누적되어 SGD보다 빠르게 이동 가능하다.
Nesterov Momentum
- 왼쪽은 현 시점의 gradient와 velocity(Momentum)를 합하여 파란색으로 weight update 방향이 결정되는 것을 볼 수 있습니다.
- 오른쪽은 velocity가 데려다줄 point를 "Look ahead"하여(살펴보아) 그 지점에서 gradient를 계산하고 이를 mix하여 방향이 결정됩니다.

- 에서 을 취함으로 식을 간편하게 할 수 있다.
AdaGrad

- gradient에 element-wise scaling을 해주는데, 그 값은 각 dimension의 누적된 제곱의 합으로 계산된다.
- per-parameter learning rate 혹은 adaptive learning rate으로 불린다.
- SGD의 문제점1케이스에서, steep한 세로 방향으로는 grad_squared가 높음으로 이를 나누면, 가던 방향으로 덜가며, flat한 가로 방향으로는 grad_squared가 낮음으로, 가던 방향으로 더 간다.
RMSProp: Leak Adagrad
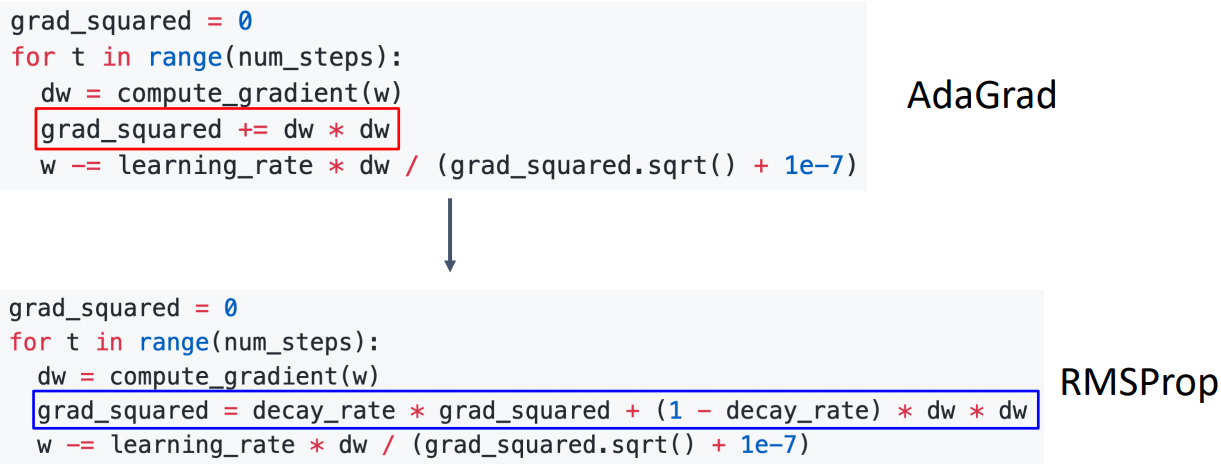
- Leak Adagrad라고 하며 과거의 grad_squared를 줄이면서 현재의 gradient를 더 많이 반영하는 방식이다.
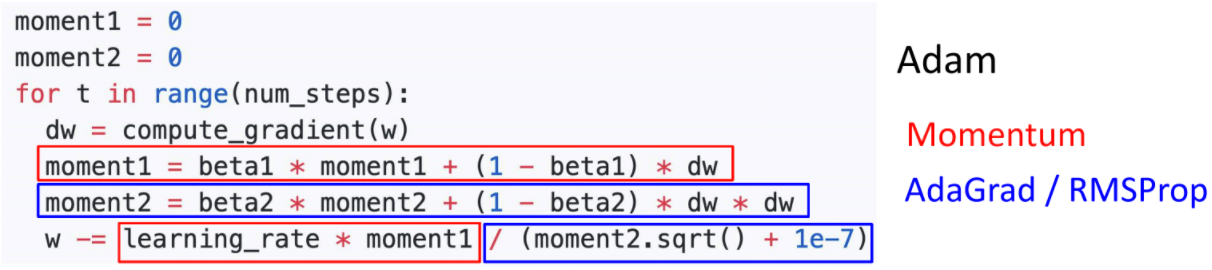
Adam (almost): RMSProp + Momentum
-
-
빨간색은 과거 dw와 현재 dw를 종합하지만 현재의 dw를 더 가중치를 줌으로 Momentum방식을 차용한 형식이다.
-
파란색은 AdaGrad와 RMSProp방식을 사용하여 dw를 제곱하여 누적함으로 방향정보를 조정한 형식이다.
-
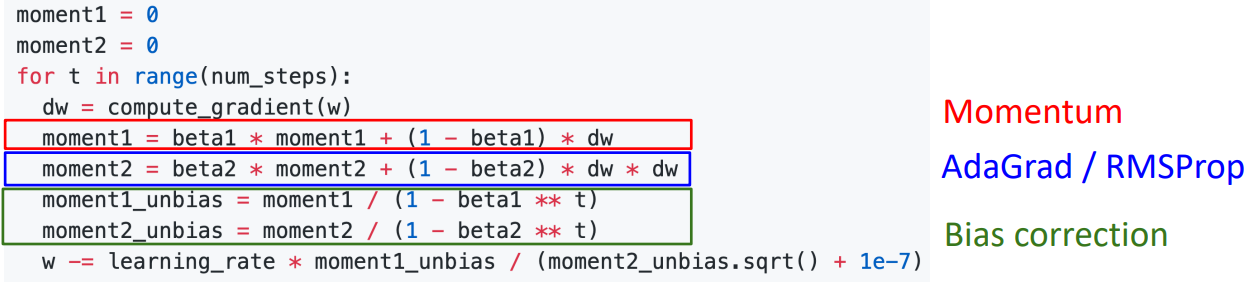
-
앞선 문제를(moment값이 0에서 시작) 개선하고자 Bias correction이 추가되었다.
-
Q: What happens at t=0? (Assume beta2 = 0.999)
A: 초기 moment2가 0이고 beta2가 1에 가까움으로 과거정보인 0값을 많이 참고하여, (분모의 해당하는 값이 0에 가까움에 따라) 초기 gradient step(이동거리)값이 굉장히 크다. -


