한 문장으로 정리하는 computer vision (12. Attention)

opcho·2021년 8월 3일

EECS 498-007 / 598-005 cs231n

computer vision

목록 보기

12/13

CS231N, EECS 498-007 / 598-005에서 나타나는 개념을 정리하기 위하여 복기용도로 작성하였습니다.
간단히 정리한 내용을 살펴보며 모르는 부분이 있을 때 찾아보는 용도로 보시면 좋을 것 같습니다.

Sequence-to-Sequence with RNNs

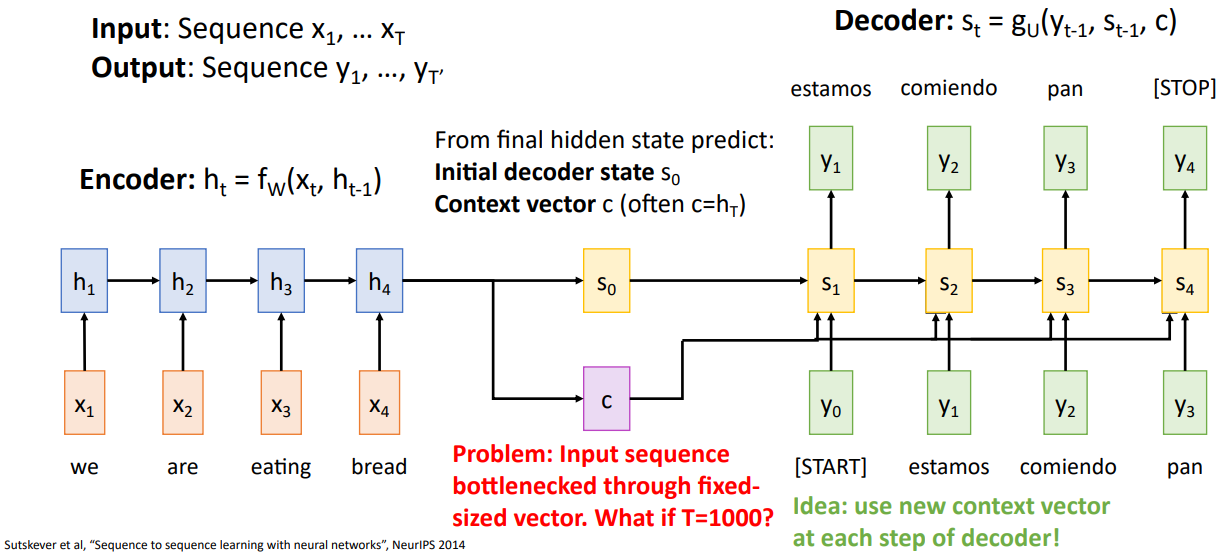
Sequence-to-Sequence구조에서, 순서 정보를 갖고 있는 $x$ 벡터와 이전의 hidden state를 입력으로 하고 다음 hidden state를 출력으로 하는 함수를 encoder network라고 한다.
encoder의 출력으로 decoder network에 사용할 초기 decoder state: $s_0$ 와 매 time step에 사용되는 context vector: $c$ 가 있다.
decoder의 구조로는 start token인 $y_0$ 와 encoder의 출력 값을 입력으로 하여 첫 번째 출력 값을 가지고, 다음 step부터는 새로운 입력 토큰이 이전 출력 토큰이 되고 hidden state는 직전 state의 출력값이 된다.
P: sequence가 굉장히 길어지면 single context vector c가 담는 내용에 한계가 있을 수 있다.
S: 새로운 형태의 context vector를 각 decoder step에 사용한다.

Sequence-to-Sequence with RNNs and Attention

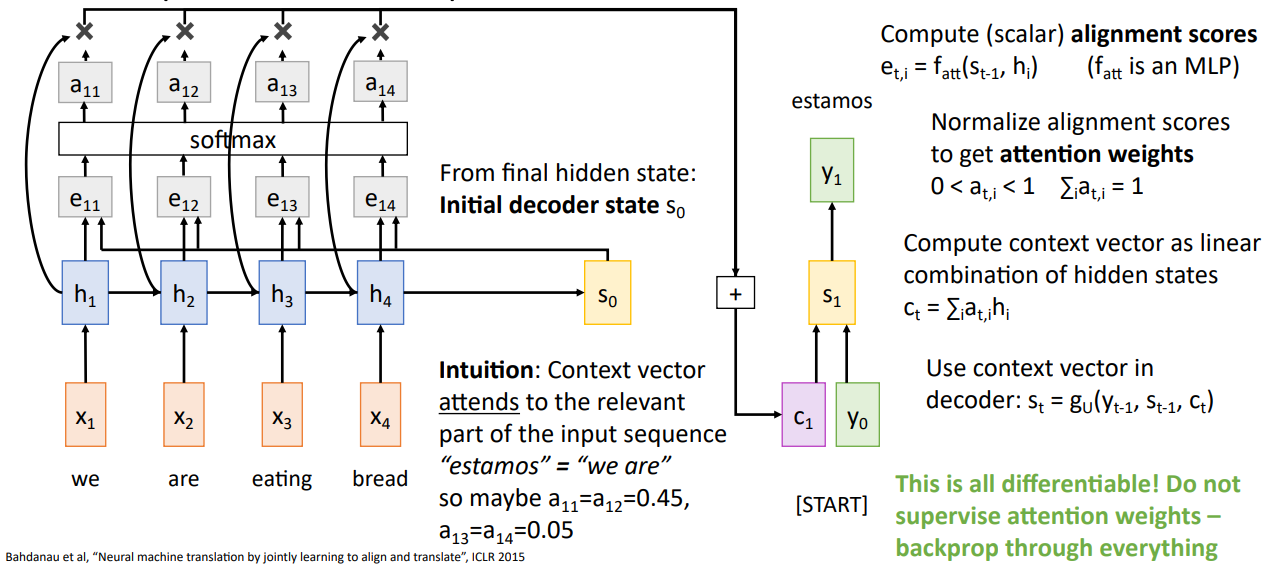
직전구조와 동일하지만 각 time step마다 새로운 context vector를 decoder의 입력값으로 사용한다.
alignment function( $f_{att}$ )을 사용하는데 매우작은 FC layer으로 입력으로는 현 시점의 decoder의 hidden state와 현 시점의 encoder의 hidden state으로 한다. 출력 값으로는 decoder의 각 hidden state에 얼마나 attend해야 하는지를 수치화한 score가 나타난다.
alignment function의 출력값으로 새로운 형태의 context vector을 만들고 decoder에서 사용한다.
alignment score를 softmax(normalize) 단계를 거쳐 probability distribution으로 만들어 출력값을 attension weight으로 한다.
encoder의 hidden state을 attension weight으로 weighted sum을 계산하여 새로운 context vector 계산한다.
Intuition: 특정 time step의 output은 input sequence의 하나 혹은 그 이상의 time step에 해당한다. 따라서 동적으로 context vector를 생성하여 input time step에 attend(focus)할 수 있게 한다.
모든 과정은 differentiable한 operations이며 직접적으로 특정 time step에 attend하라고 supervise(지시하지) 않았으며, 대신 network가 스스로 학습하게 끔 했다.
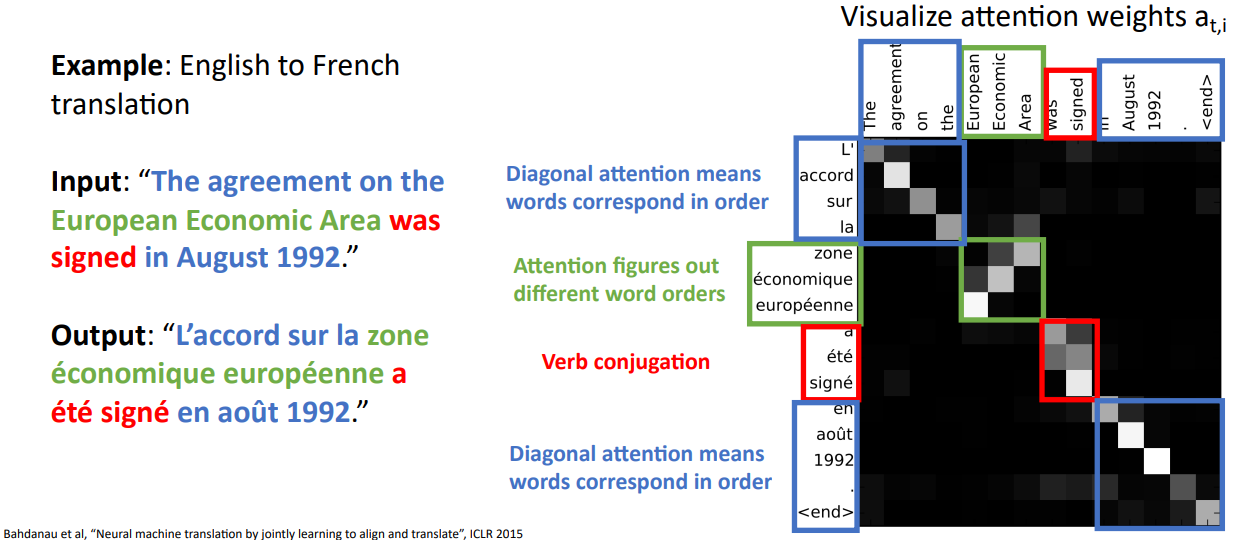
영문에서 불어로 번역할 때의 맵핑정보를 살펴보면 파란 박스 부근에서는 입력과 출력값의 순서대로 attention weight가 반영되는 것을 살펴 볼 수 있지만, 빨간 박스 및 초록 박스에서는 역순으로 반영되거나 복잡하게 구성됨을 알 수 있다.
RNN으로 구성한 seq-to-seq은 decoder가 encoder의 hidden state를 unordered set으로 보았다면, attention은 hidden state를 ordered한 sequence으로 판단했다.

Image Captioning with RNNs and Attention

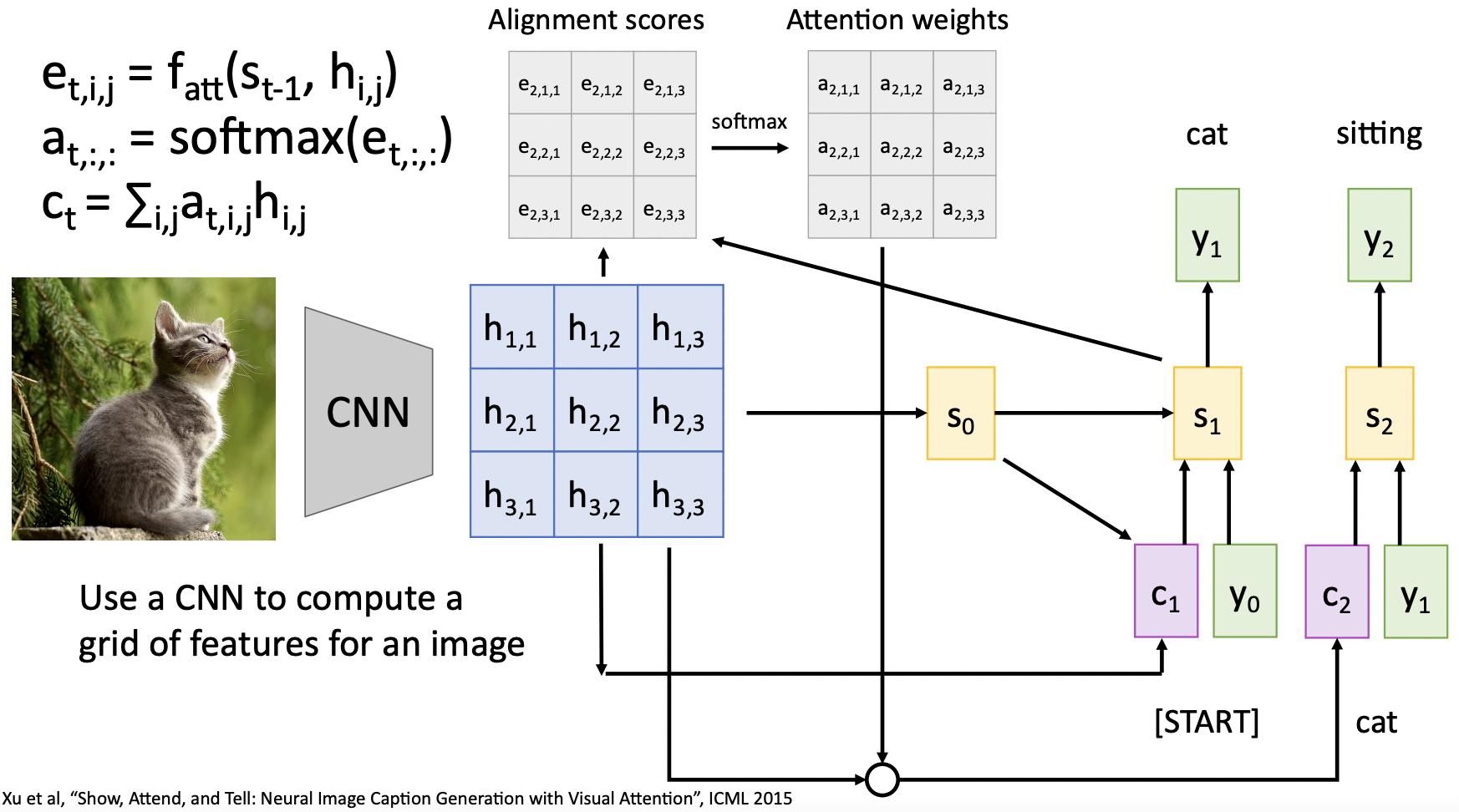
seq-to-seq구조와 비슷하게 CNN을 통한 feature vector(h)와 decoder network의 직전 hidden state(s)를 입력으로하여 feature vector의 반영 정도를 결정할 allignment score를(e) 계산한다.
이후 allignment score를 softmax함수를 통해 (총 합이 1이되는) 확률분포로 normalize한다.
마찬가지로 allignment weight와(a) feature vector(h)의 weighted combination을 통해 context vector(c)를 계산한다.

Generalize Attention

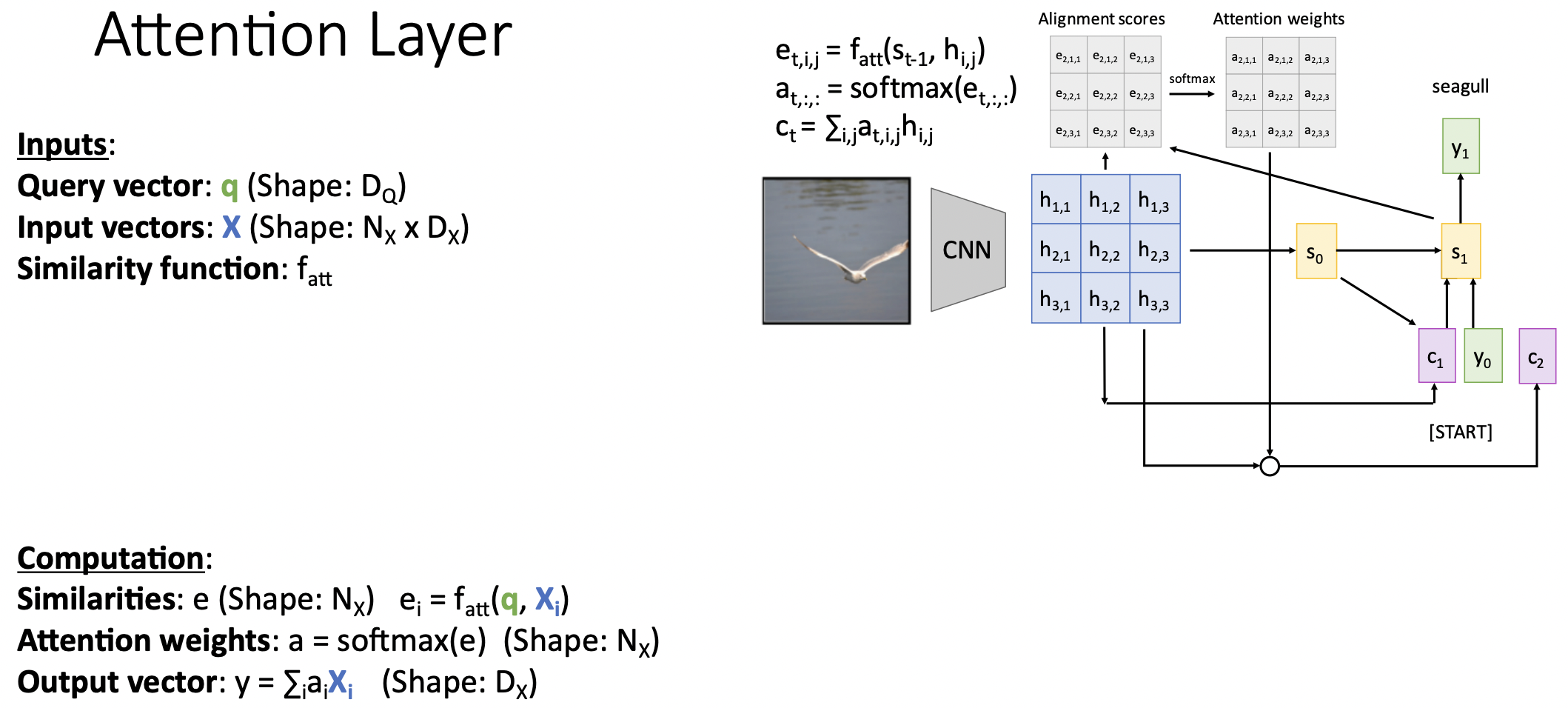
직전 예제에서의 context vector를 query vector으로 대치한다.
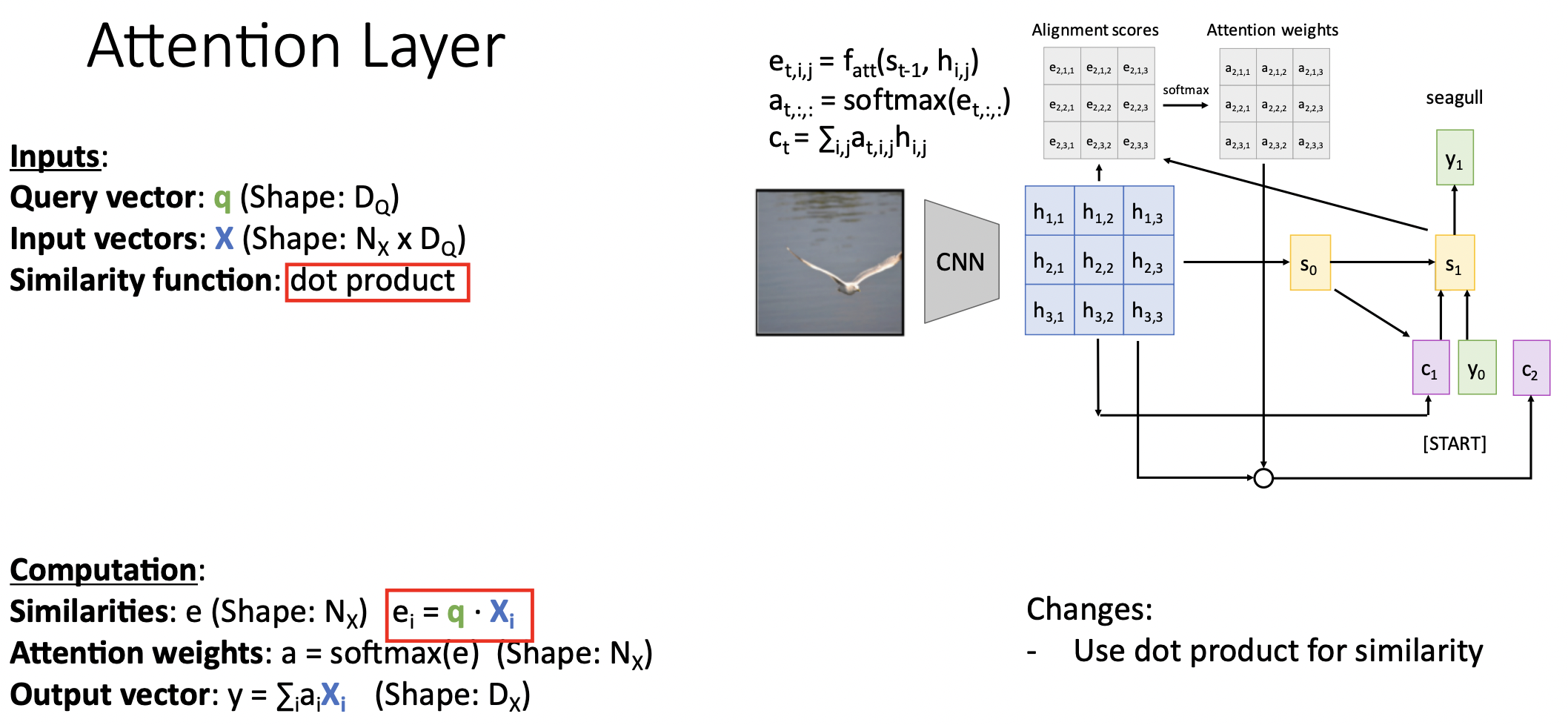
일반화의 시도로 similarity function: $f_{att}$ 를 dot product으로 바꿔보았다. 연산이 더욱 효율적이고 잘 작동했다.
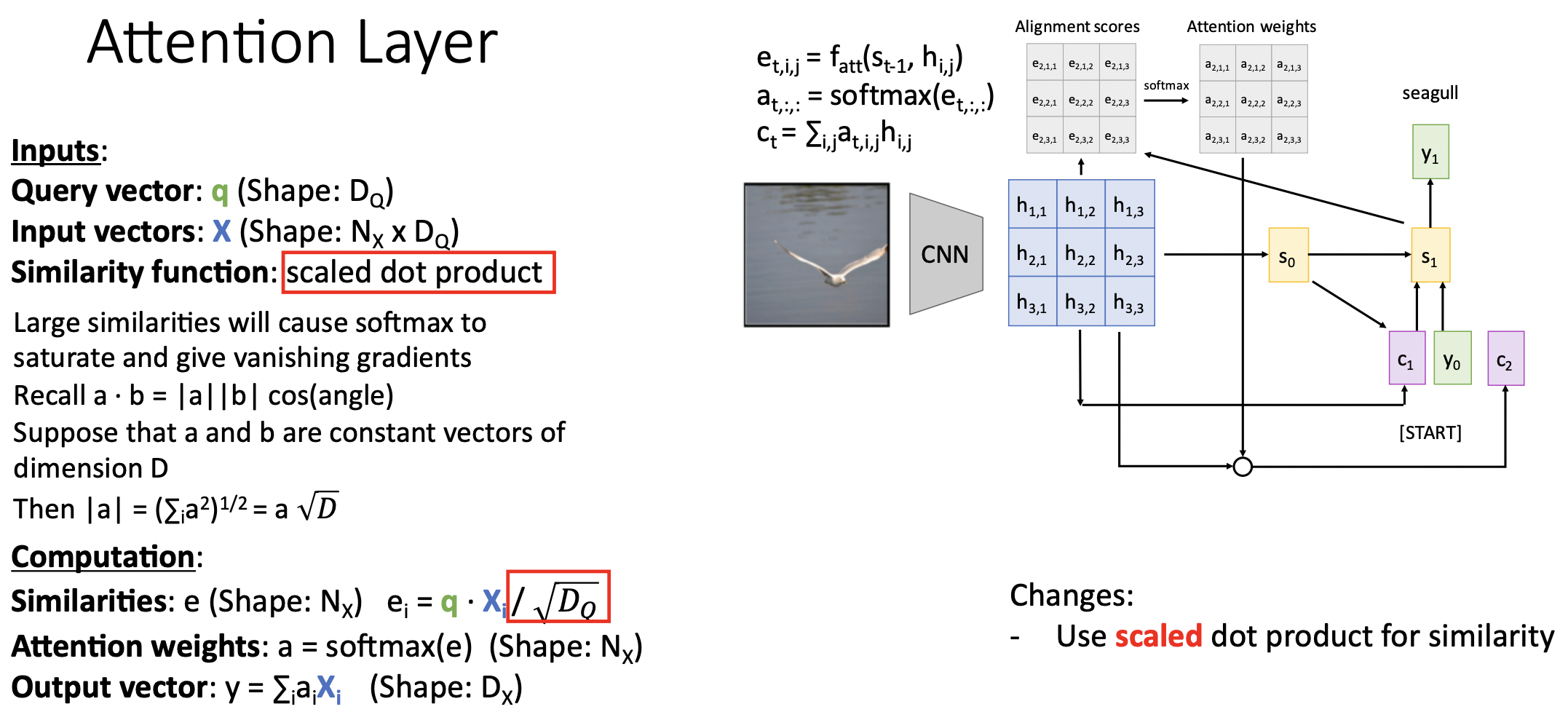
추가적으로 query vector와 input vector의 차원을 scaling 해주었다. 왜냐하면 이 결과를(similarities)를 곧바로 softmax함수를 통과시킬 것인데 높은 값이 입력으로 들어온다면 vanishing gradient descent과정이 예상되기 때문이었다. 그렇다면 높은 값을 가진 부분외에는 softmax 통과한 값이 0에 근사하여 입력값의 쏠림 현상이 발생하기 때문이다.(saturated)
차원이 D으로 같은 두 constant a,b벡터를 dot product할 때, a벡터의 magnitude는 $|a|=(\sum_{i}a^2)^{1/2}=a\sqrt{D}$ 으로 표현된다.
그렇다면 매우 고차원일때 magnitude a가 매우 높은 값을 가질 수 있다. 이런 현상을 방지하기 위해 D차원의 sqrt를 나눠주었다.
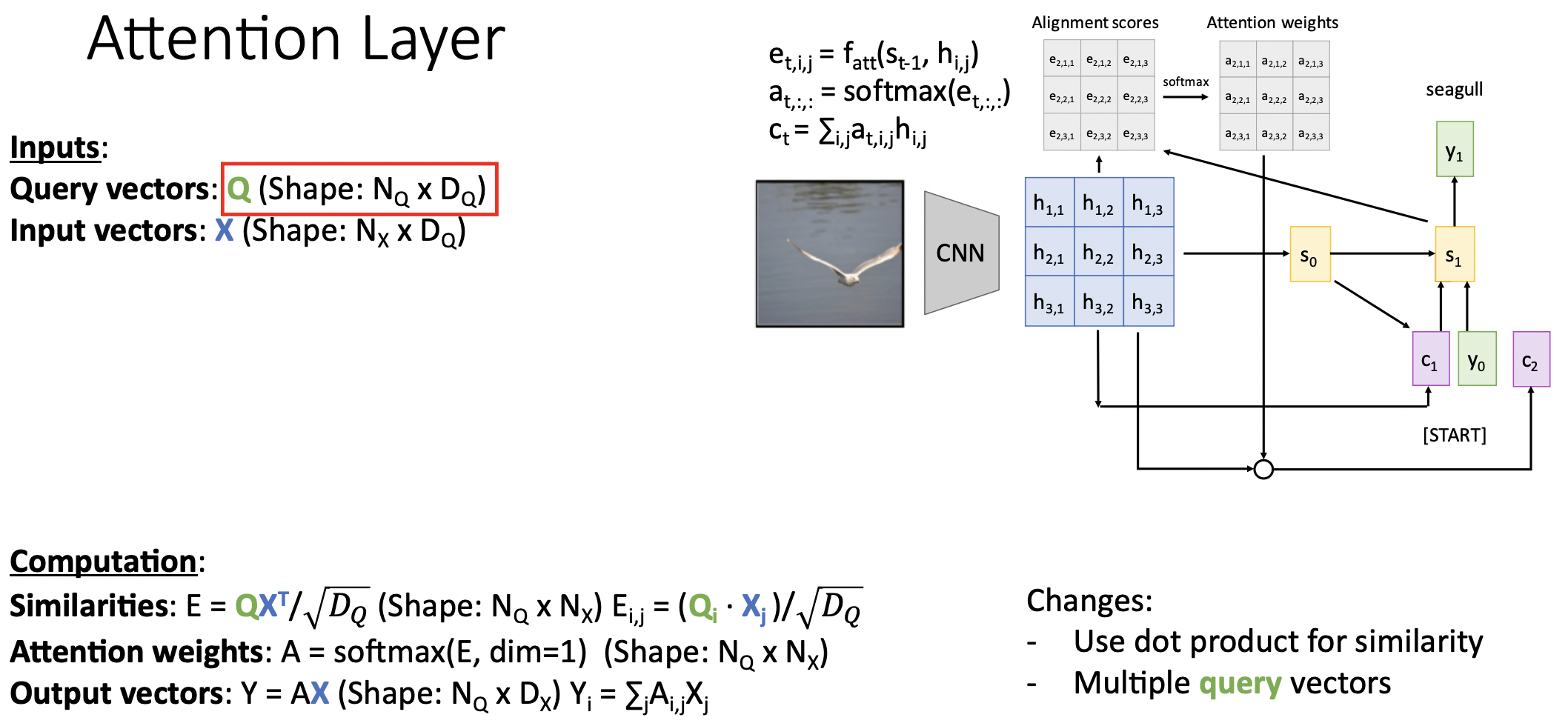
query vector 또한 seq를 지닌 형태로 나타내며, (여러 timestep에서의)qeury vector를 반영한 형태로 진화하였다.
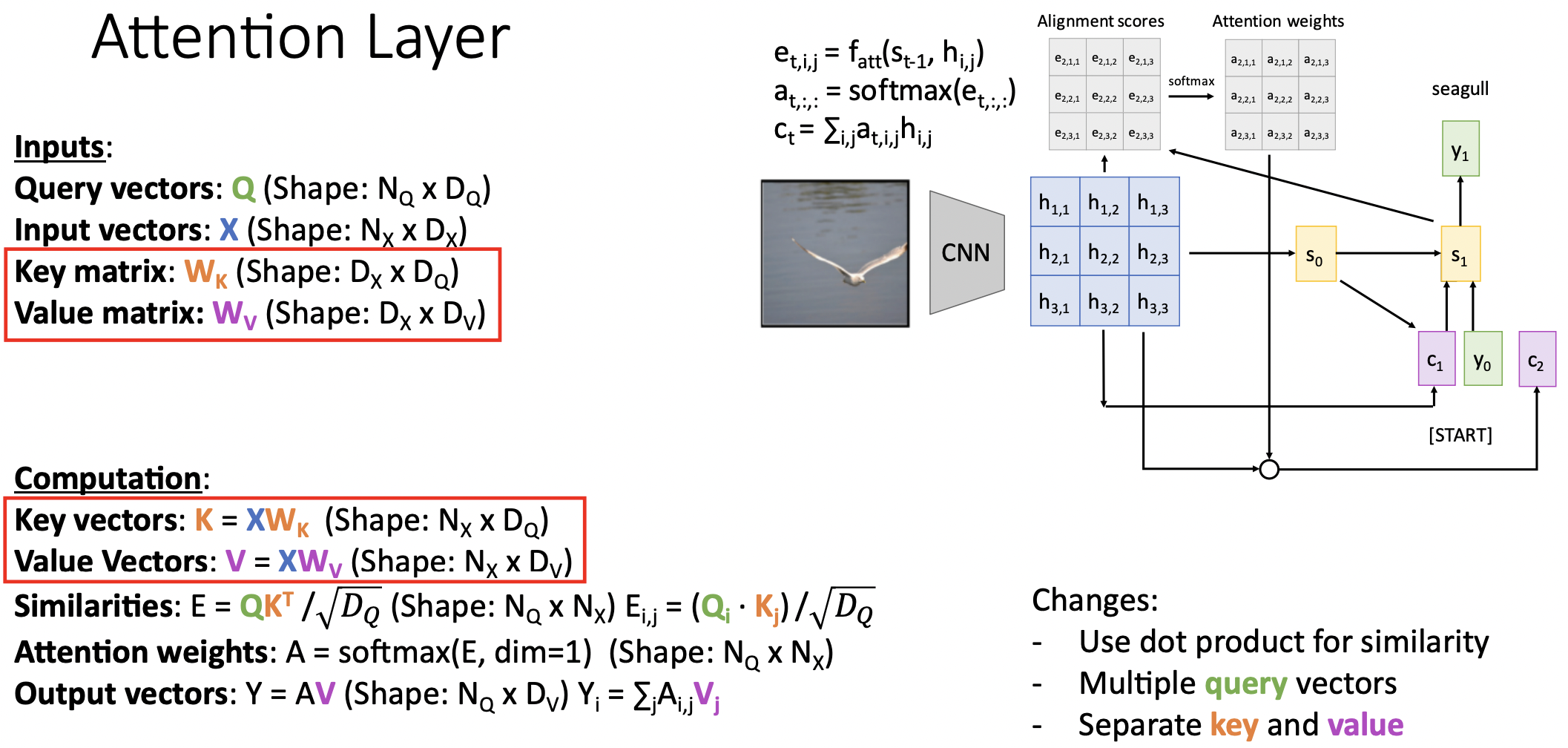
input vector가 attention weight 계산과정과 output vector 계산과정에 두번이나 다른 목적으로 사용하고 있다. 따라서 input vector을 학습가능한 key&value matrix으로 구분하였다.
key matrix는 attention weight 계산에, value matrix는 output vector 계산에 사용된다.
모델이 input data를 사용할 때 flexibility를 부여한다. query vector의 feature정보를 계산할 때 필요한 input vector의 영역과 output vector계산 시에 사용할 input vector의 영역을 구분하는 의미로 보인다.

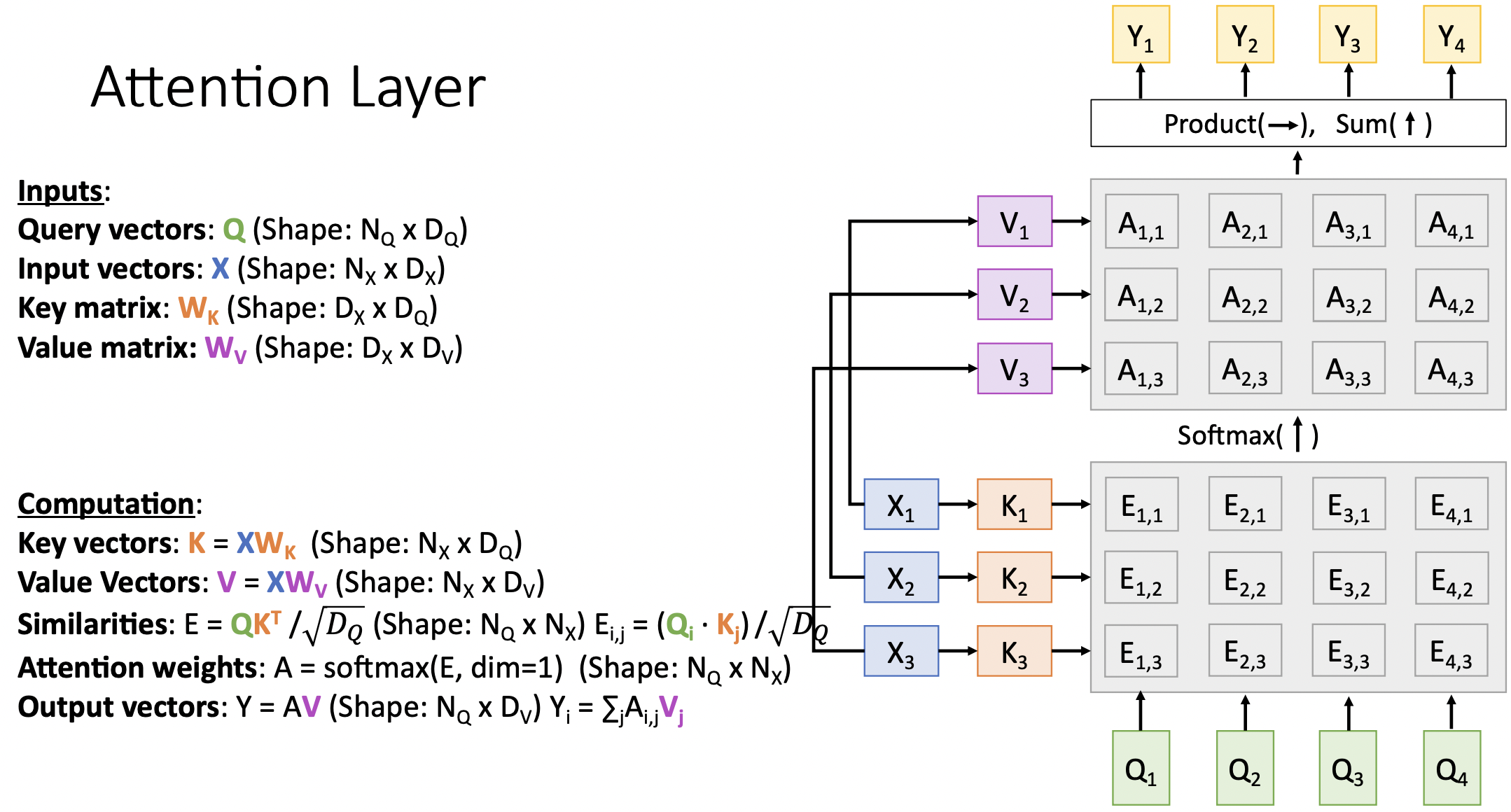
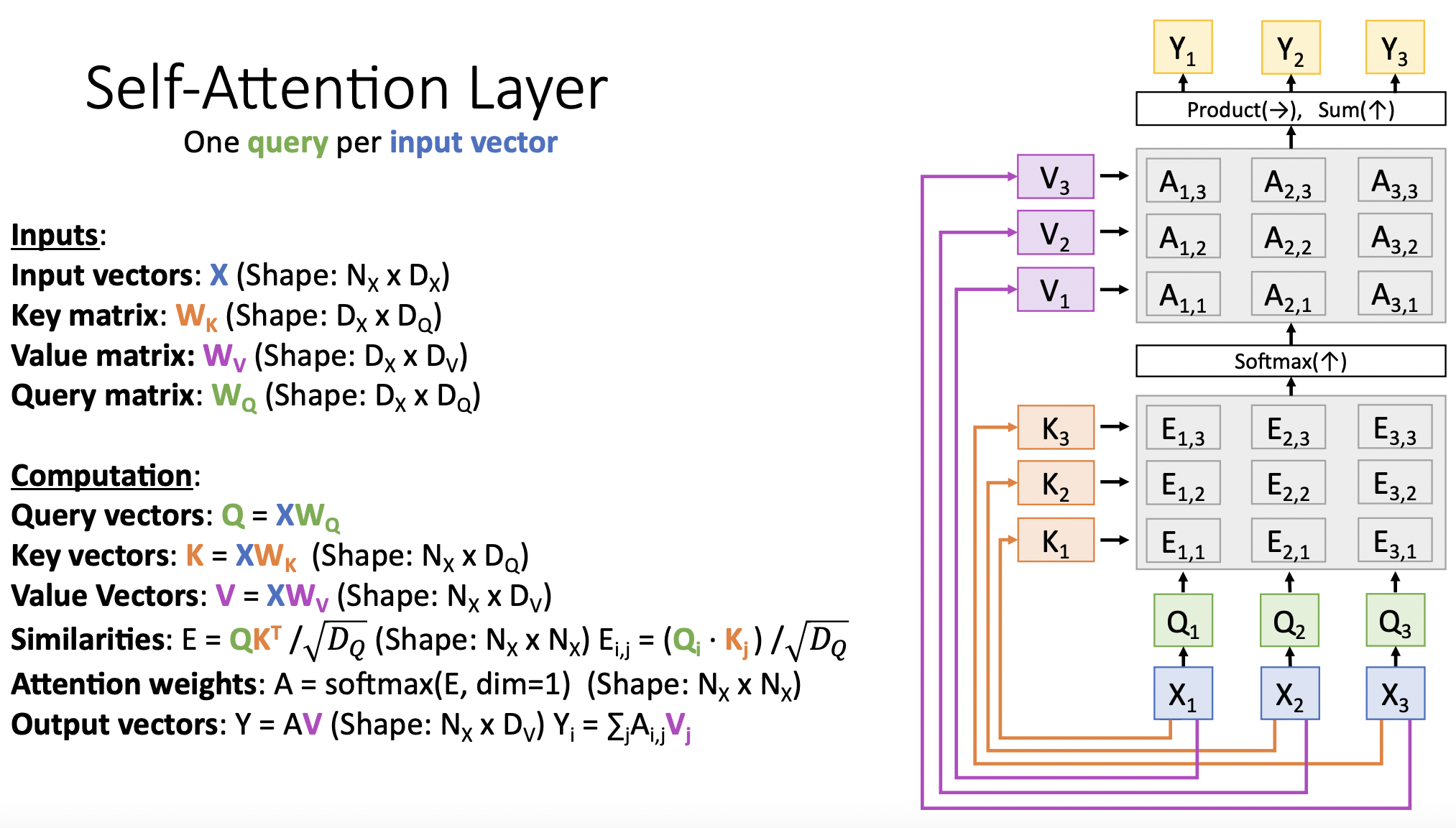
Self-Attention Layer

input vector와 query matrix의 곱으로 query vector을 구한다.
input vector와 key matrix의 곱으로 key vector를 구한다.
query vector와 key vector에서 similiarities(E)를 구한다.
E를 softmax통과하여 attention weight를 계산한다.
input vector와 value matrix의 곱으로 value vector를 구한다.
value vector와 attention weight를 곱하여 output vector를 계산한다.

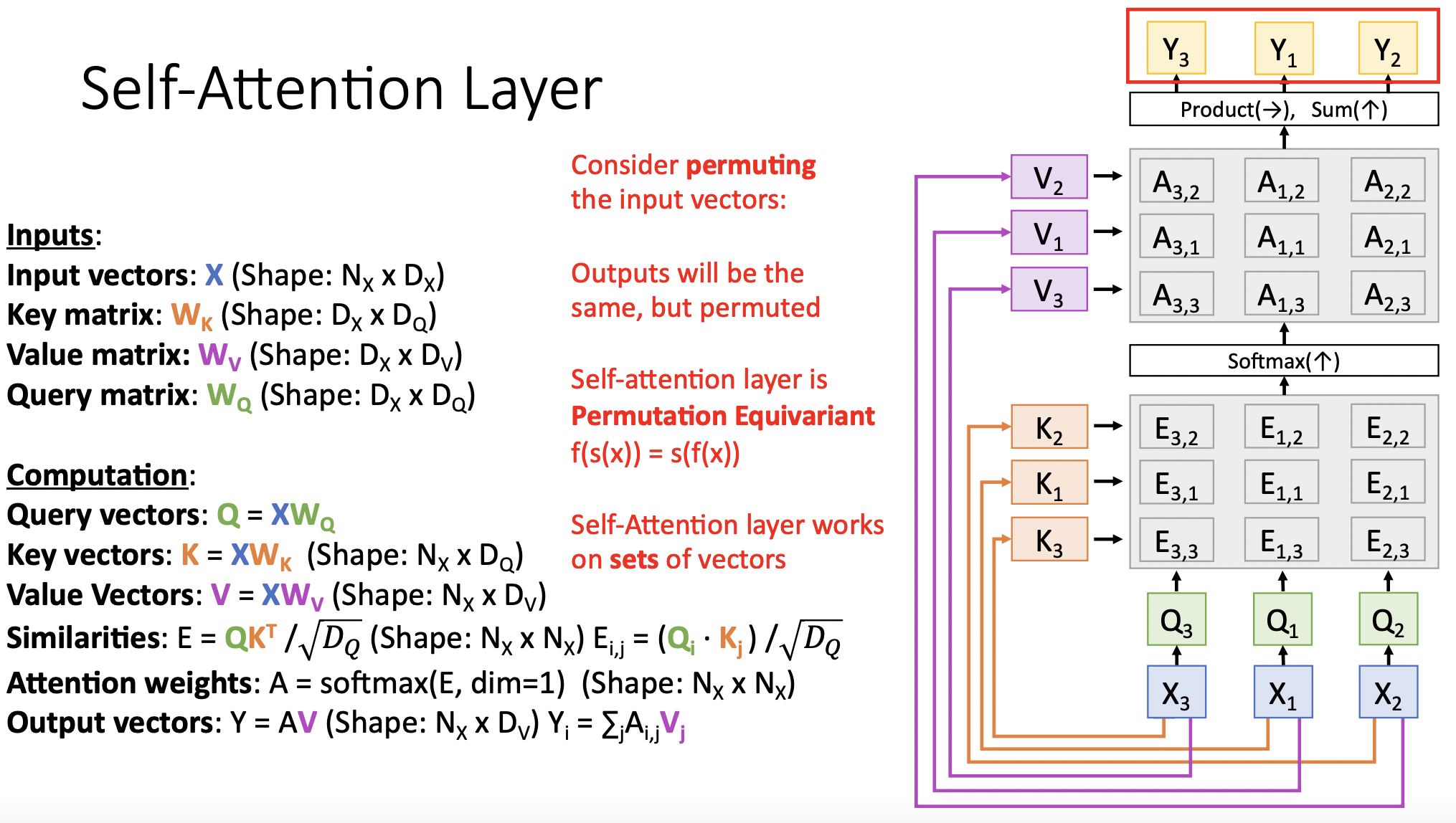
input vector의 순서를 [3,1,2]으로 바꿔준다면 어떻게 될까
바뀐순서대로 key vector와 query vector가 계산된다.(순서는 독립적으로 계산되기 때문), 마찬가지로 value vector, attention weight, similarities, output vector 모두 각각의 값은 그대로인체 순서만 바뀌어 계산된다.
self-attention operation은 permutation equivariant하다
: $f(s(x))=s(f(x))$
self-attention은 입력값의 순서에 상관하지 않는다. 단순히 벡터 집합을 연산할 뿐이다. 따라서 벡터처리의 순서에 대한 결과를 모르기 때문에, 필요한 경우 입력값에 positaional encoding을(학습가능한 lookup table을 만들어) concat해야 한다.

Masked Self-Attention Layer

현재 sequence의 결과가 다음 sequence의 결과를 참고하는 행위를 막기위해서 similarities에 막으려는(mask) 정보를 음의 무한대 값으로 설정한다. 언어모델에서 주로 사용된다.

Multihead Self-Attention Layer

self-attention layer을 병렬적으로(multihead) 구성한 것으로 ,독립적인 head의 갯수 H와 Query dimension 인 $D_Q$ 만을 hyperparameter으로 삼고 있다.

Example: CNN with Self-Attention

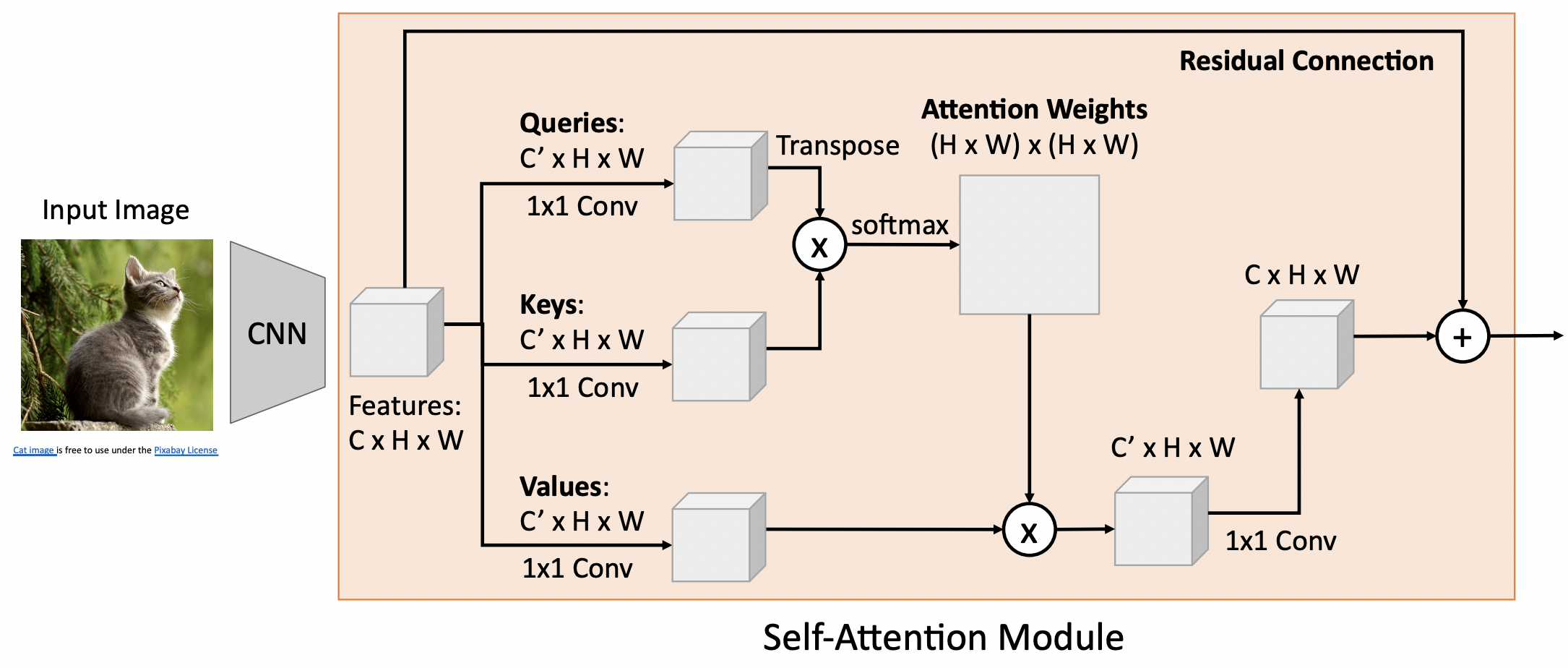
CNN을 통과한 fearture(CxHxW)를 독립적으로 구성된 1x1 conv를 통과 시켜 queries, keys, values를 얻는다.
queries와 keys의 결과를 (transpose,) inner product(, softmax)하여 attetion weights[(H,W),(H,W)]를 얻는다.
attetion weights와 values를 weighted linear combination(후 1x1 conv)을 하여 새로운 feature(CxHxW)을 구하고 이를 residual connection으로 연결한다.
새로운 타입의 layer으로 기존 레이어에 추가로 구성하여 쌓을 수있다.

Three Ways of Processing Sequences

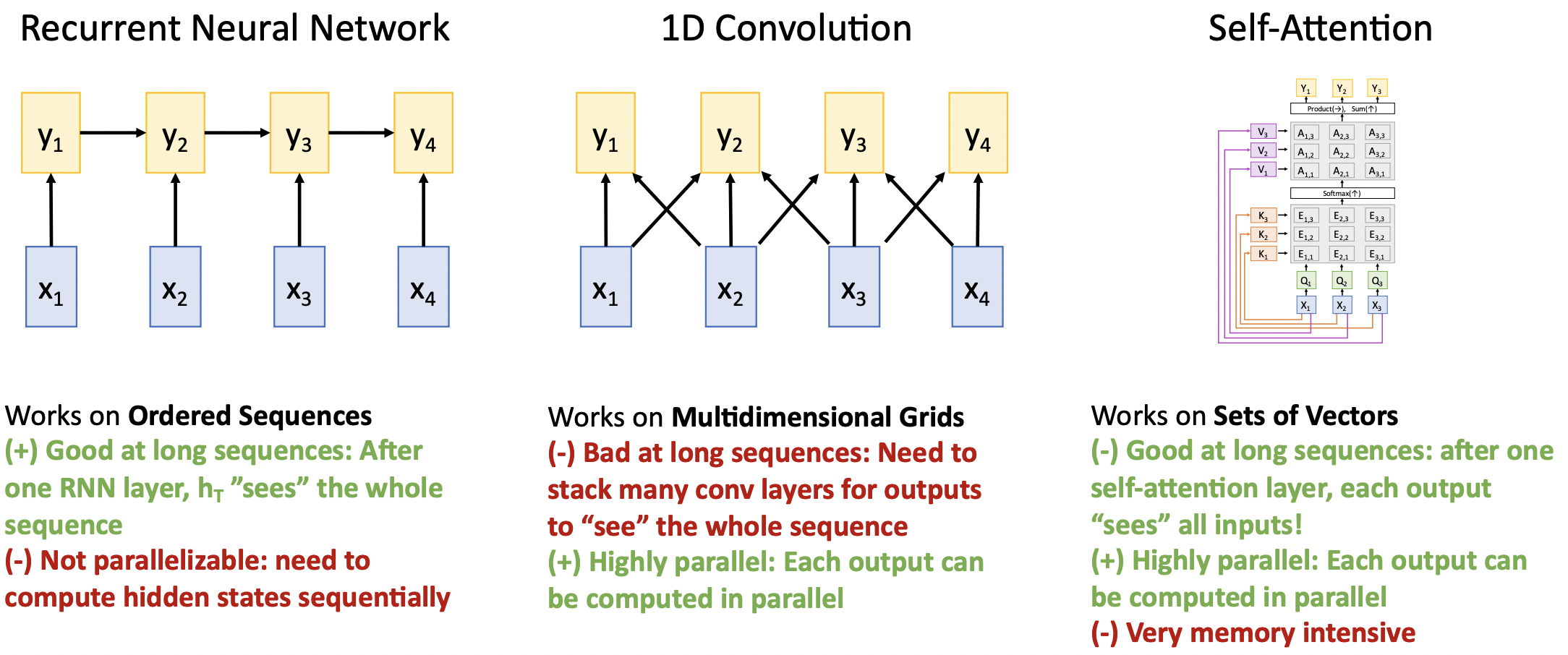
RNN
- 장점: 긴 seq 처리에 좋다. 모든 timestep의 hidden state는 입력 seq의 전체 정보를 담고 있다.
- 단점: 직전 timestep의 state가 계산되어야 다음 timestep이 계산가능하다. 연속적으로 계산되어야 하기때문에 병렬처리가 장점인 GPU사용에 한계점이 있다.(sequential depedency) 모델의 확장성에 무리가 있다.
1D Conv
- 장점: RNN과 달리 output seq가 필요로하는 input값이 정해저있어 병렬처리가 가능하다.
- 단점: output이 긴 seq를 포함하기에는 layer를 많이 쌓아야한다.
Self-Attention
- 장점: 긴 seq 처리에 좋다. 각 output은 모든 input정보를 담고 있다. matrix연산과정만 있음으로 병렬처리가 가능하다.
- 단점: 메모리가 많이 요구된다.
이 레이어들의 정보를 어떻게 종합할지 고민될 때, 종합한 논문이 Attention is all you need이다. seq layer처리에 오직 Self-Attention만 사용한다.

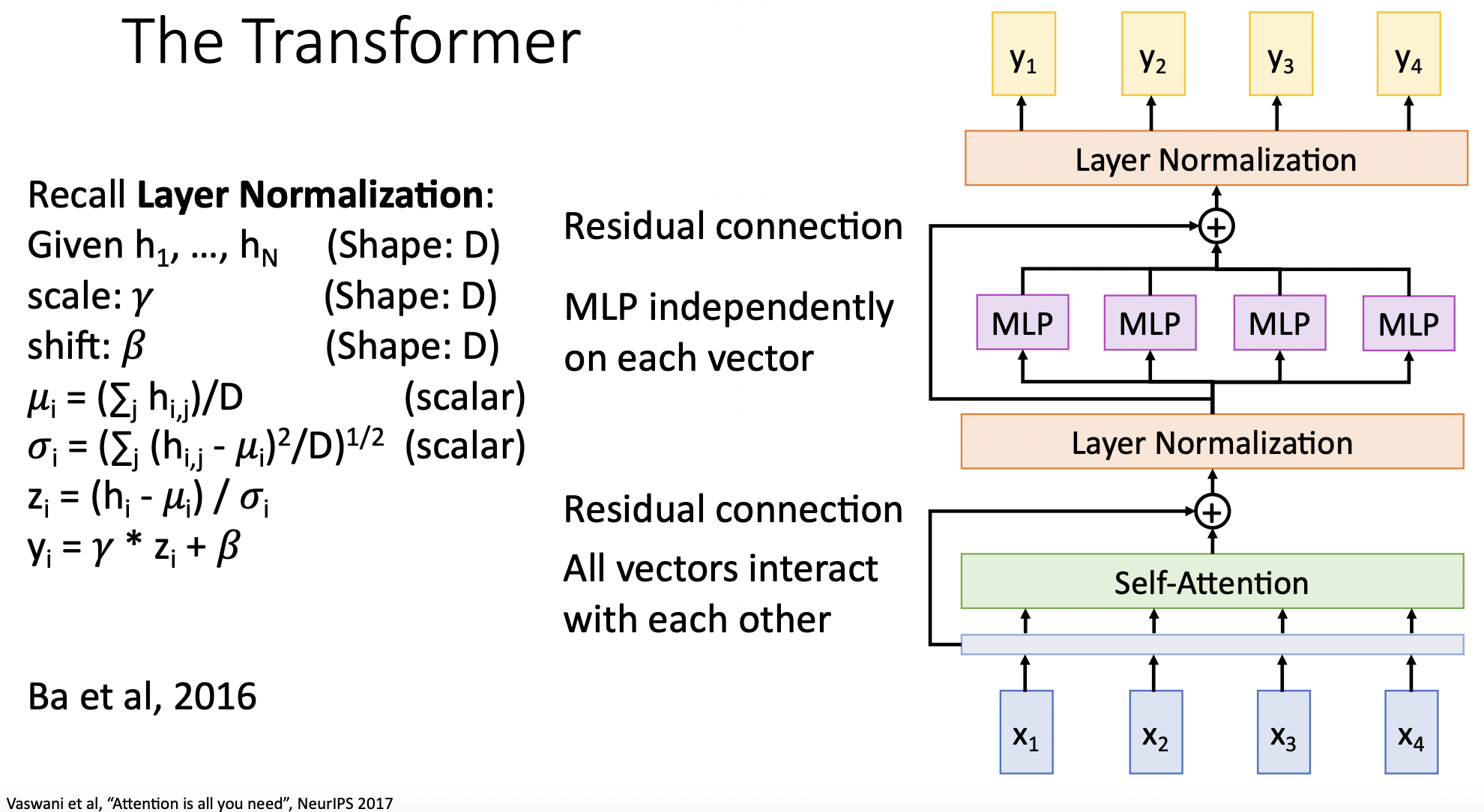
The Transformer

seq데이터(x)를 (multiple head를 가진) self-attention 레이어를 통과한 뒤 residual connection을 한다.(gradient flow에 도움)
layer norm을 적용한다. (optimization에 도움, seq model에서는 layer norm이 좋다고 한다.) 각각의 output vector에 대하여 독립적으로 norm을 적용하므로 상호 벡터간의 communication이 없다.
output 벡터를 독립적인 MLP을 통과 시킨다.
residual connection과 layer norm을 적용시킨다.

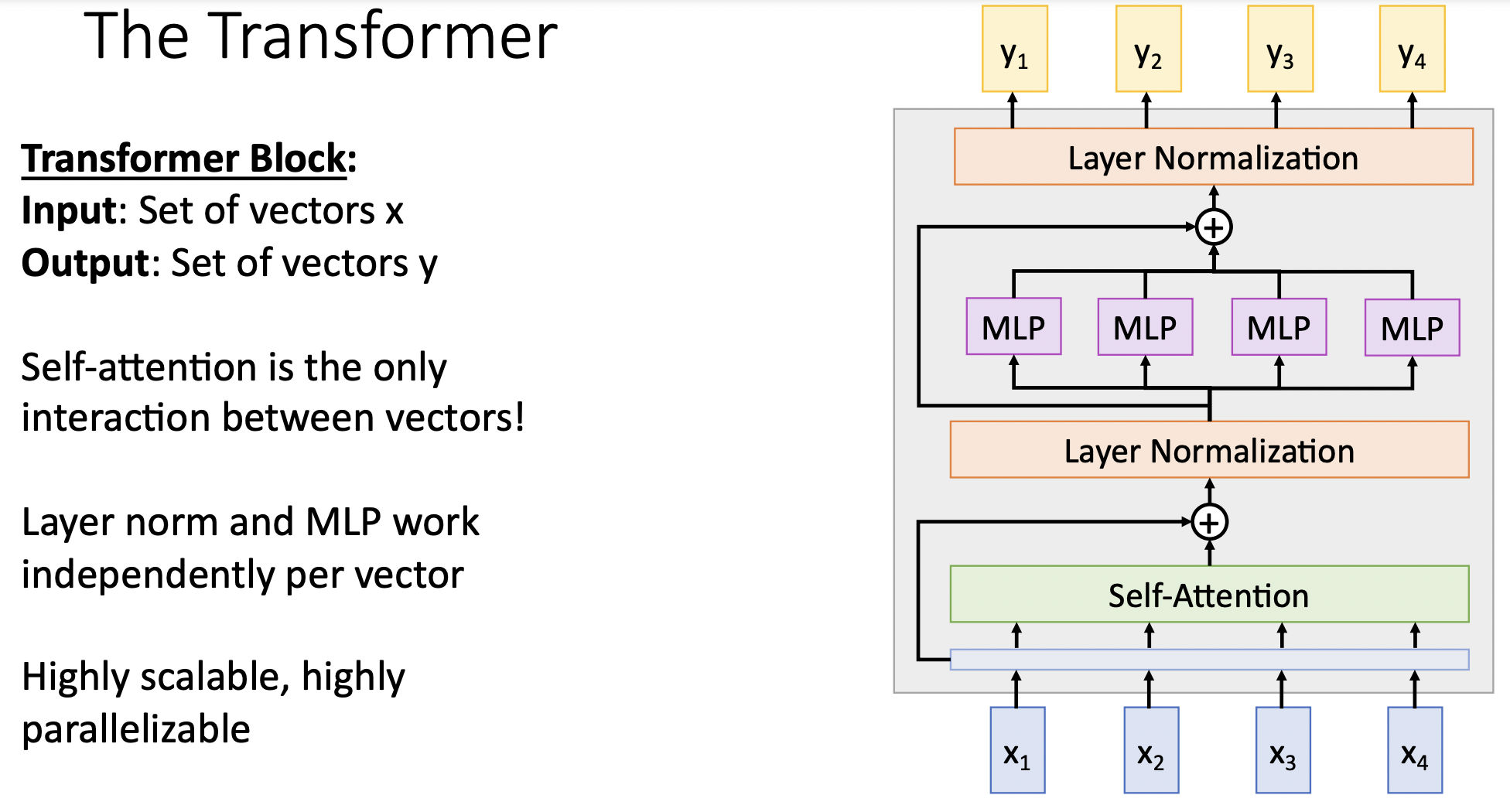
위의 전체 단계를 transformer block으로 구성한다.
내부의 self-att 레이어만이 벡터간 interaction이 일어나는 부분이다.
입출력 벡터의 dim은 달라질 수 있다. 병렬처리와 확장성이 좋다.
기존 이미지처리의 방식인 pretrain model을 사용하고 finetuning 과정을 적용하는 것을 자연어 처리에도 동시에 적용이 가능해 졌다.(transformer 덕에)
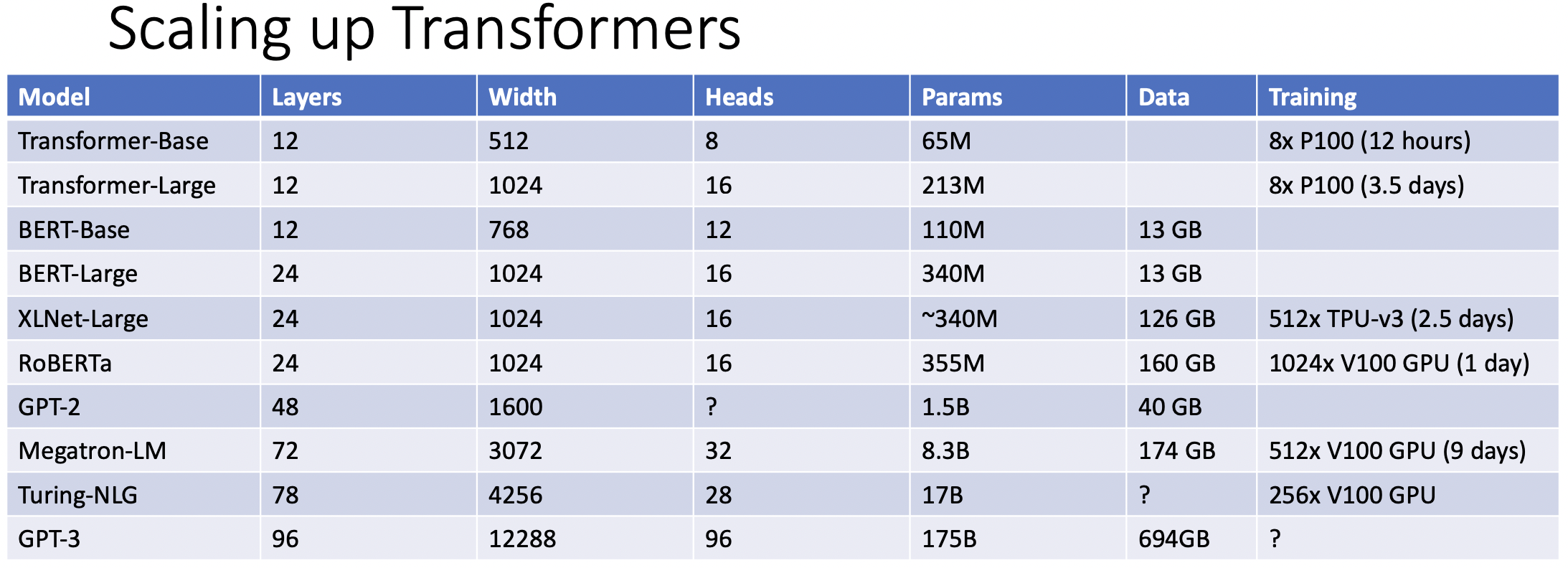
언어모델의 발전가능성은 얼마나 많은 transformer를 사용할 수 있는지으로 바뀌었다.