한 문장으로 정리하는 computer vision (6. Convolutional Networks)

opcho·2021년 7월 15일

computer vision

목록 보기

6/13

CS231N, EECS 498-007 / 598-005에서 나타나는 개념을 정리하기 위하여 복기용도로 작성하였습니다.
간단히 정리한 내용을 살펴보며 모르는 부분이 있을 때 찾아보는 용도로 보시면 좋을 것 같습니다.

Convolutional Neural Networks (CNNs / ConvNets)

ordinary Neural Networks과 관계
- 공통점
  - 학습 가능한 가중치(weight)와 바이어스(bias)로 구성
  - 각 뉴런은 입력을 받아 내적 연산(dot product)을 한 뒤 선택에 따라 비선형(non-linear) 연산
  - 마지막 레이어에(SVM/Softmax와 같은) 손실 함수(loss function)을 가지며, 우리가 일반 신경망을 학습시킬 때 사용하던 각종 기법들을 동일하게 적용할 수 있다.
- 차이점
  - ConvNet 아키텍쳐는 입력 데이터가 이미지라는 가정 덕분에 이미지 데이터가 갖는 특성들을 인코딩 할 수 있다.
  - 네트워크를 학습시키는데 필요한 모수 (parameter)의 수를 크게 줄일 수 있게 해준다.
특징
- ConvNet 아키텍쳐에서는 크게 컨볼루셔널 레이어, 풀링 레이어, Fully-connected 레이어라는 3개 종류의 레이어가 사용된다.
- 각 레이어는 3차원의 입력 볼륨을 미분 가능한 함수를 통해 3차원 출력 볼륨으로 transform시킨다.
- 모수(parameter)가 있는 레이어도 있고 그렇지 않은 레이어도 있다 (FC/CONV는 모수를 갖고 있고, RELU/POOL 등은 모수가 없음).
- 초모수 (hyperparameter)가 있는 레이어도 있고 그렇지 않은 레이어도 있다 (CONV/FC/POOL 레이어는 초모수를 가지며 RELU는 가지지 않음).
- 레이어의 각 뉴런을 입력 볼륨의 로컬한 영역(local region)에만 연결할 것이다. 이 영역은 리셉티브 필드 (receptive field, filter size와 동일한 의미)라고 불리는 초모수 (hyperparameter) 이다
- 왜 CONV 레이어에 stride 1을 사용할까? 보통 작은 stride가 더 잘 동작한다. 뿐만 아니라, stirde를 1로 놓으면 모든 spatial 다운샘플링을 POOL 레이어에 맡기게 되고 CONV 레이어는 입력 볼륨의 깊이만 변화시키게 된다.
- 왜 (제로)패딩을 사용할까? CONV 레이어를 통과하면서 spatial 크기를 그대로 유지하게 해준다는 점 외에도, 패딩을 쓰면 성능도 향상된다. 만약 제로 패딩을 하지 않고 valid convolution (패딩을 하지 않은 convolution)을 한다면 볼륨의 크기는 CONV 레이어를 거칠 때마다 줄어들게 되고, 가장자리의 정보들이 빠르게 사라진다.

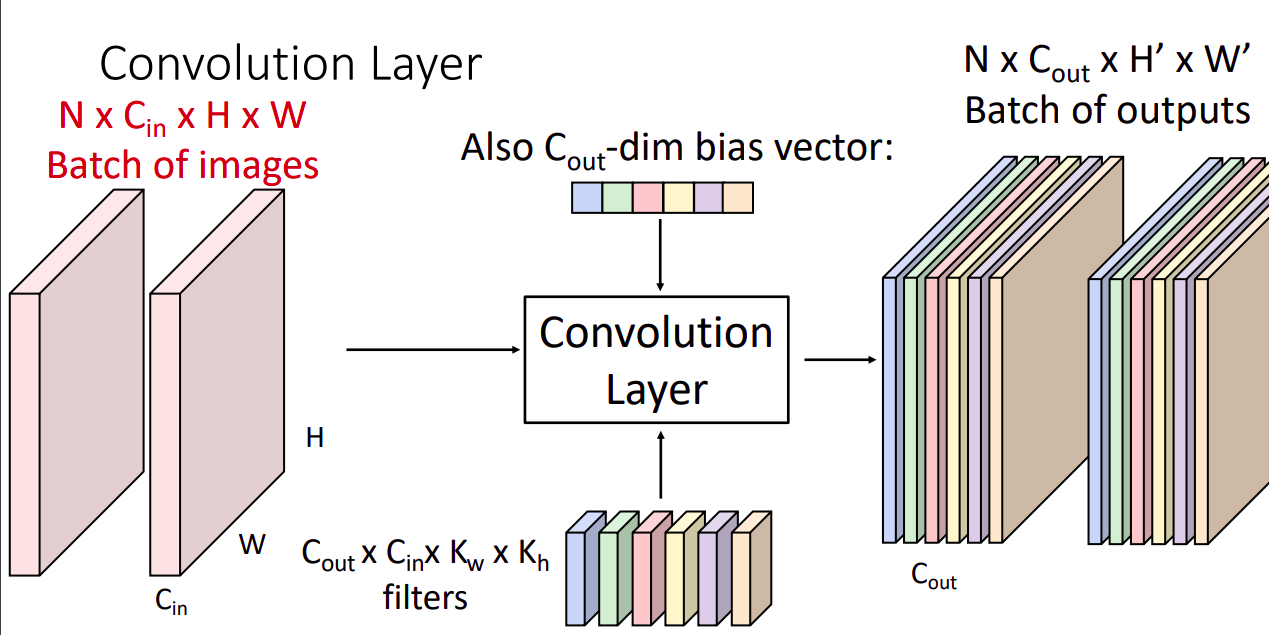
Q: What happens if we stack two convolution layers?
FC layer때와 마찬가지로( $y=W_1*W_2*x$ ) 다른 형태의 conv layer가 된다.
층을 쌓기 위해서는 레이어 사이에 activation layer를 추가한다.

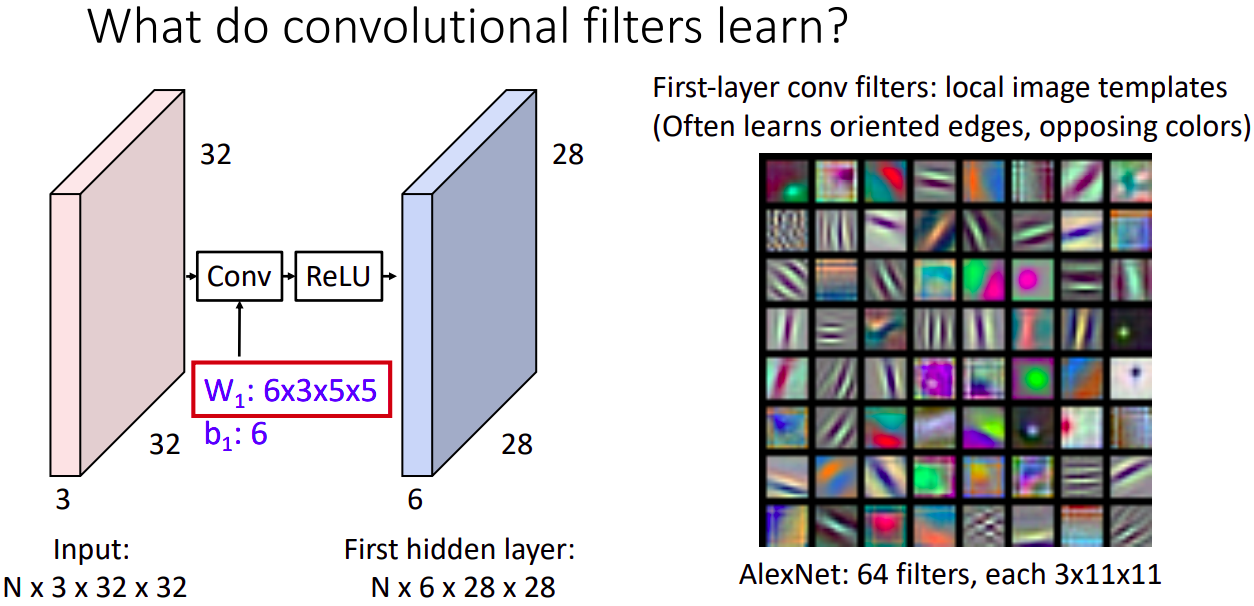
Q: conv layer 는 무얼 배우나?
A: 첫번째 레이어는 보통 edge의 방향이나 반대되는 색을 나타낸다.

Q: 필터를 계속 먹이면서, Input image를 보존하고 싶은데, 이미지 사이즈가 줄어드는 단점이 있다. 결과적으로 표현되는 픽셀 수가 줄어들어, 다양한 패턴들이 줄어드는 문제가 생긴다.
A: activation map의 사이즈가 계속 줄어드는 단점을 해결하기 위한 방안으로는 padding이 있다. Padding이란 Input 이미지 주변에 0 픽셀을 두르는 것이다. 그렇다면 Padding을 몇으로 설정할 것인지도 정해야한다. 주로 input과 같은 크기의 output을 내기 위해, (K -1) / 2로 패딩값을 정한다.

출력 크기와 보편적 세팅 값은 알아두면 좋은 내용이다.

Q: input volume: 3 x 32 x 32, 10 5x5 filters with stride 1, pad 2
A: Output size

Output volume size
- (32 + 2 x 2 - 5)/1 + 1 = 32 spatially, so 10 x 32 x 32
Number of learnable parameters: 760
- Parameters per filter: 3 x 5 x 5 + 1 (for bias) = 76,
- 10 filters, so total is 10 x 76 = 760
Number of multiply-add operations: 768,000
- 10 x 32 x 32 = 10,240 outputs
- each output is the inner product of two 3(입력 채널) x 5 x 5(커널 사이즈) tensors (75 elems)
- total = 75 x 10240 = 768K

receptive field

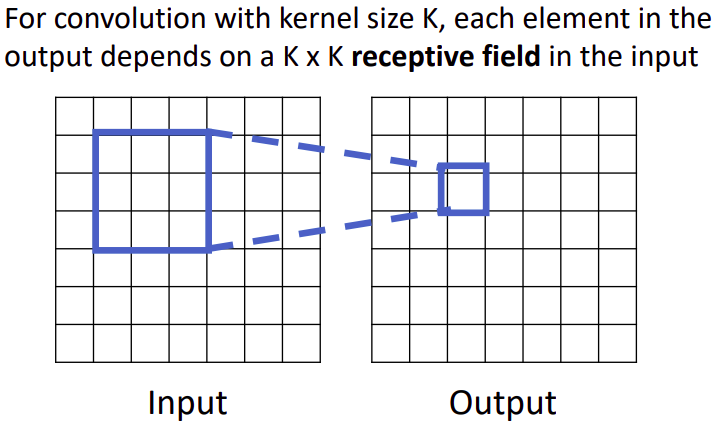
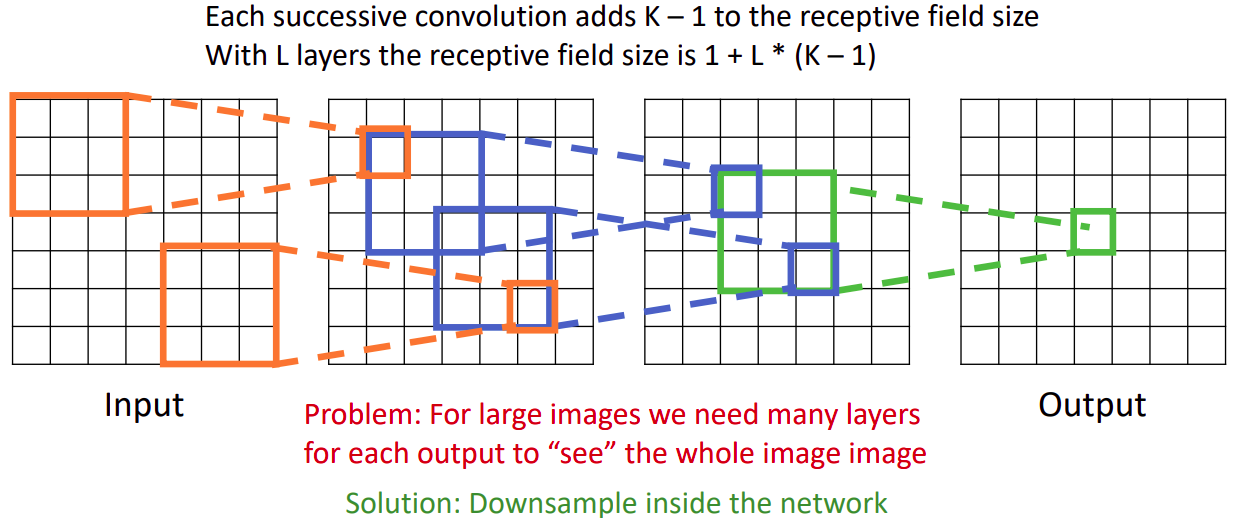
output의 한 칸을 생성하기 위해서, 필터가 적용된 영역을 receptive field라고 한다.
연속적인 RF는 RF size에 K-1만큼 곱해준다.L-th layer의 RF size는 1+L*(K-1)이다.

Q: "receptive field in the input” vs “receptive field in the previous layer”
A: 특정 아웃풋의 해당하는 입력값크기(레이어 깊을수록 선형적으로 증가) VS 컨볼루션의 커널사이즈

P: Input 이미지가 커질 때, input 이미지 픽셀 전체를 리셉티브 필터로 가져가려면, 아주 많은 layer가 필요하다.
S: 리셉티브 필드를 넓게 가져가는 다른 방법은 down sample 사용하는 것이다. (stride를 설정하면 깊게 쌓지 않아도 된다.)

Pooling Layer

특징
- ConvNet 구조 내에 컨볼루션 레이어들 중간중간에 주기적으로 풀링 레이어를 넣는 것이 일반적이다.
- 풀링 레이어가 하는 일은 네트워크의 파라미터의 개수나 연산량을 줄이기 위해 representation의 spatial한 사이즈를 줄이는 것이다. 이는 오버피팅을 조절하는 효과도 가지고 있다.
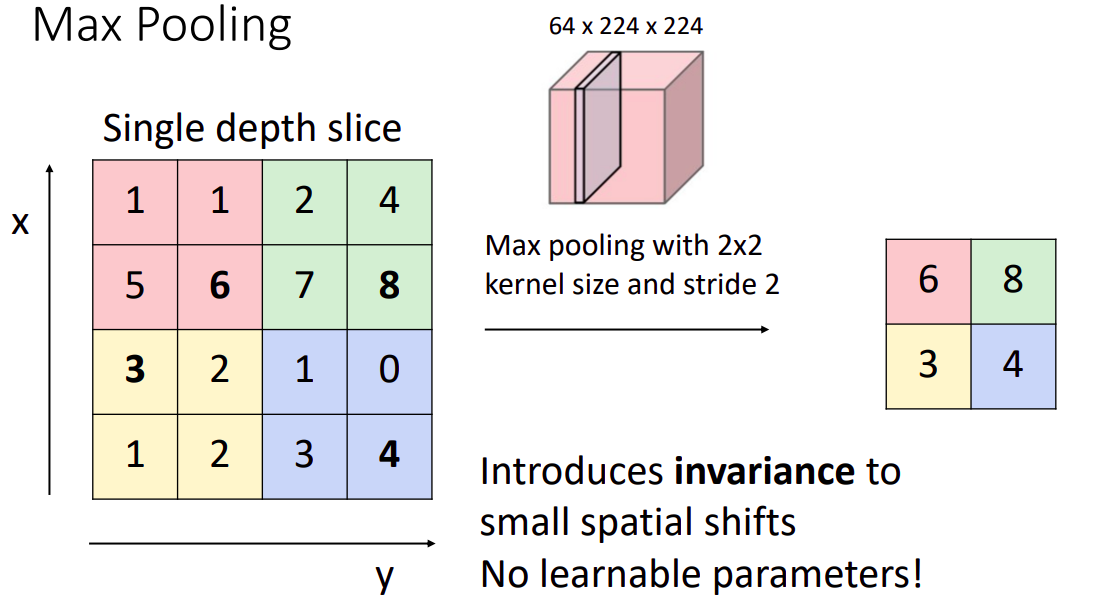
- 풀링 레이어는 MAX 연산을 각 depth slice에 대해 독립적으로 적용하여 spatial한 크기를 줄인다.
- Max 풀링 뿐 아니라 average 풀링, L2-norm 풀링 등 다른 연산으로 풀링할 수도 있다. 최근에는 Max 풀링이 더 좋은 성능을 보이며 더 많이 쓰인다.
- 최근에는 representation의 spatial한 사이즈를 줄이기 위해 CONV 레이어에서 더 큰 stride를 사용하며, VAE(variational autoencoder) 또는 GAN(Generative Adversarial Network)과 같은 모델을 훈련하는 데 풀링을 없애는 것이 좋은 성능을 나타내었다. 미래의 아키텍처에는 풀링 레이어가 거의 또는 전혀 없을 것 같습니다.

Batch Normalization

개요

the outputs of a layer를 Normalize 함으로 zero mean and unit variance를 갖는다.
왜 하나면 “internal covariate shift”(직전 레이어가 최적화 됨에 따라 그 결과값의 분포가 차이난다. 따라서 직후의 레이어의 학습에 영향을 준다.)를 줄여준다. 이를 통해 stationary(standardized) distribution한 입력값을 갖게 만들어 improves optimization.
We can normalize a batch of activations like this: $\hat{x}=\frac{x-E[x]}{\sqrt{Var[x]}}$
이 과정은 미분가능한 함수를 사용함으로(differentiable function) 네트웍의 연산자로 사용할 수 있어 backprop이 가능하다.
직전 레이어가 최적화 됨에 따라 그 결과값의 분포가 차이가 심할 수 있다. 이를 0을 평균으로하고 분산이 1인형태로 분포를 조정하여 학습기간 동안 stationary(standardized) distribution한 입력값을 갖게 만든다.
위 과정을 통해 최적화 프로세스를 stablize & accelerate 하는 효과가 있길 희망?한다. 아마 다음 수업에서 관련된 내용을 들을 수 있다고 합니다.

특징

Q: zero mean and unit variance를 만들기 힘들때는 어떻게 해?
A: 새로운 파라미터인 감마&베타를 출력 값을 조정하는 scale&shift 용도로 설정한다.

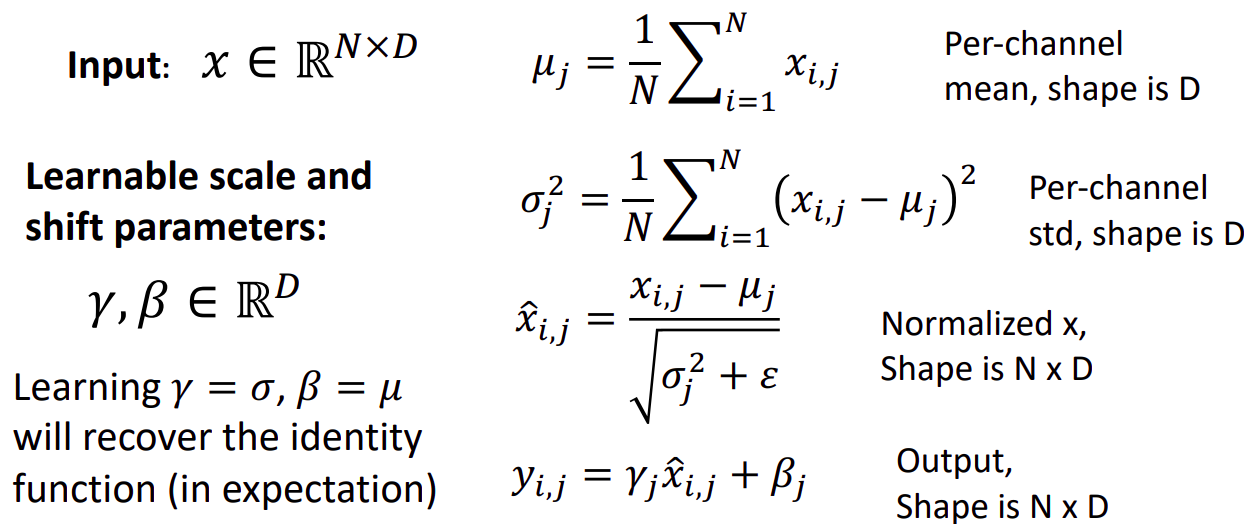
Q: Estimates depend on minibatch; can’t do this at test-time!
A: 학습 할 때의 사용한 평균과 분산 값의 평균을 그대로 사용한다. 따라서 수행과정이 linear하게 연산되어(단순히 상수값을 사칙연산하고 학습된 감마와 베타값을 쓰기때문) computational overhead가 0이 된다.

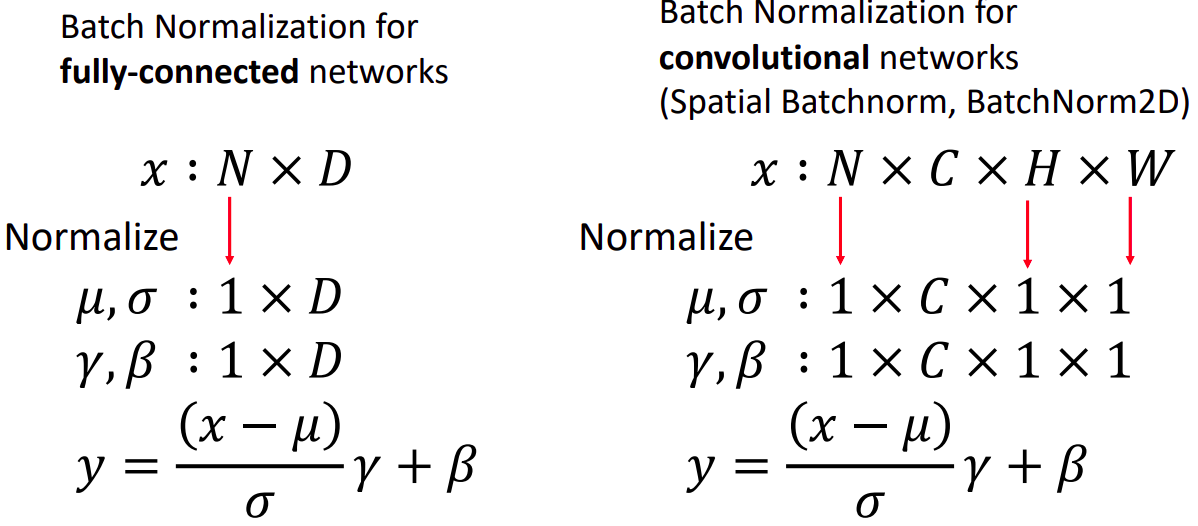
FC 레이어에서는 batch 단위의 Normalization를, CONV 에서는 batch&spatial 단위의 Normalization를 수행한다.

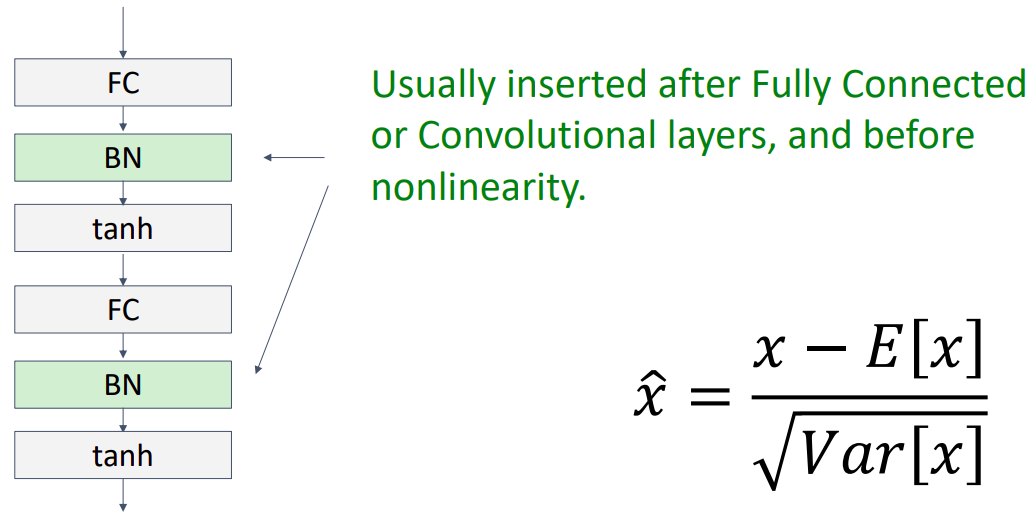
그림과 같이 보통 FC, CONV 레이어 뒤에 그리고 nonlinearity 앞에 위치함을 볼 수 있다.

장점
1. Makes deep networks much easier to train!
2. Allows higher learning rates, faster convergence
3. Networks become more robust to initialization
4. Acts as regularization during training
5. Zero overhead at test-time: can be fused with conv!
단점
1. Not well-understood theoretically (yet).
  (저스틴은) 이론적으로 정확한 설명과 증명이 덜 되었다도 합니다.
2. Behaves differently during training and testing: this is a very common source of bugs!
  데이터의 imbalance 혹은 train & test mode 설정에 문제가 있을 경우 버그가 잘 발생한다고 합니다.

Layer Normalization

BN이 train time과 test time에 동작 과정이 다르게 수행되는것이 문제점으로 시작
(테스팅 시에 특정 레이어의 모드가 다르게 동작하는것이 다른 레이어에 비 생산적이게 작동하여 문제라고 합니다.)
따라서 batch dimension의 평균을 구하는 것이 아닌 feature dimension의 평균을 구함으로서 다른 batch에 의존적이지 않게 동작하기 때문에 train & test time시 동작과정이 동일하다고 합니다.
RNN, Transformer에서 주로 사용됨

Instance Normalization

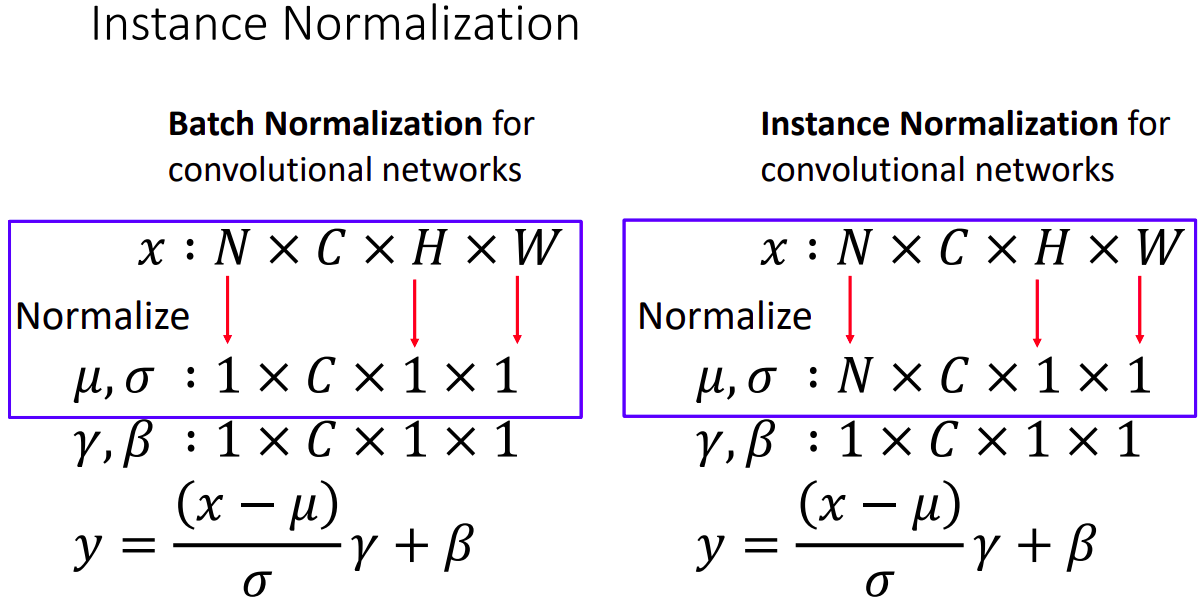
CONV 레이어에서도 같은 문제점을 해결하기 위해 batch와 spatial dimension의 normalize 대신 spatial dimension(H,W) 만 normalize함으로 train & test time시 동작과정이 동일하다고 합니다. (batch에 의존적이지 않게 동작하기 때문에)

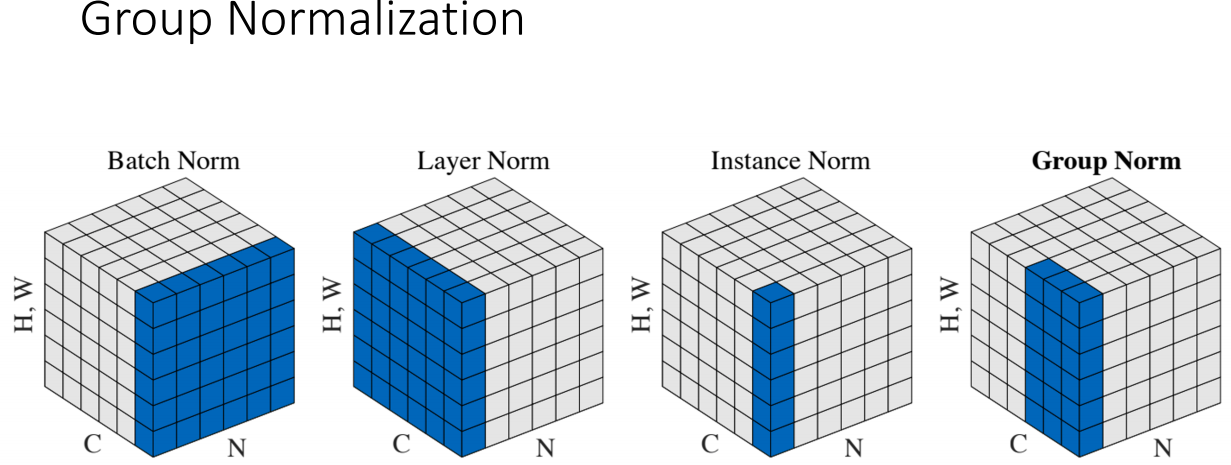
Group Normalization & Summary

batch dimension : N
channel dimension : C
spatial dimension : H, W

batch Norm: average over batch & spatial dimension
Layer Norm: average over channel & spatial dimension
Instance Norm: average over channel dimension
Group Norm: channel dimension을 몇가지 그룹으로 나누어 그룹단위의 norm을 적용한다.
최근 Object detection에서 사용됨