CS231N, EECS 498-007 / 598-005에서 나타나는 개념을 정리하기 위하여 복기용도로 작성하였습니다.
간단히 정리한 내용을 살펴보며 모르는 부분이 있을 때 찾아보는 용도로 보시면 좋을 것 같습니다.
학습 후기
가독성을 위하여 불가피하게 강의자료가 늘어가며, 강의 내용이 점점 더 많아지고 있습니다.
조만간 assignment도 연결지어 포스팅 할 계획입니다.
Activation functions
- 이전 레이어에서의 (linear한 특성을 가지고 있는) 함수의 결과 값을 non-linear한 특성을 가진 activation function을 통과시켜 다음 레이어에 전달한다.
- 네트워크에서 Activation function을 제거한다면 단순히 하나의 linear한 레이어가 되버린다. 따라서 레이어 계층 설정에 중요한 부분을 담당하고 있다.
Activation Functions: Sigmoid
- probability에 대한 interpretation(해석)으로 이해 할 수 있다. 각각의 뉴런이 On/Off되는 현상을 0과1사이의 값으로 표현 할 수 있기 때문이다.
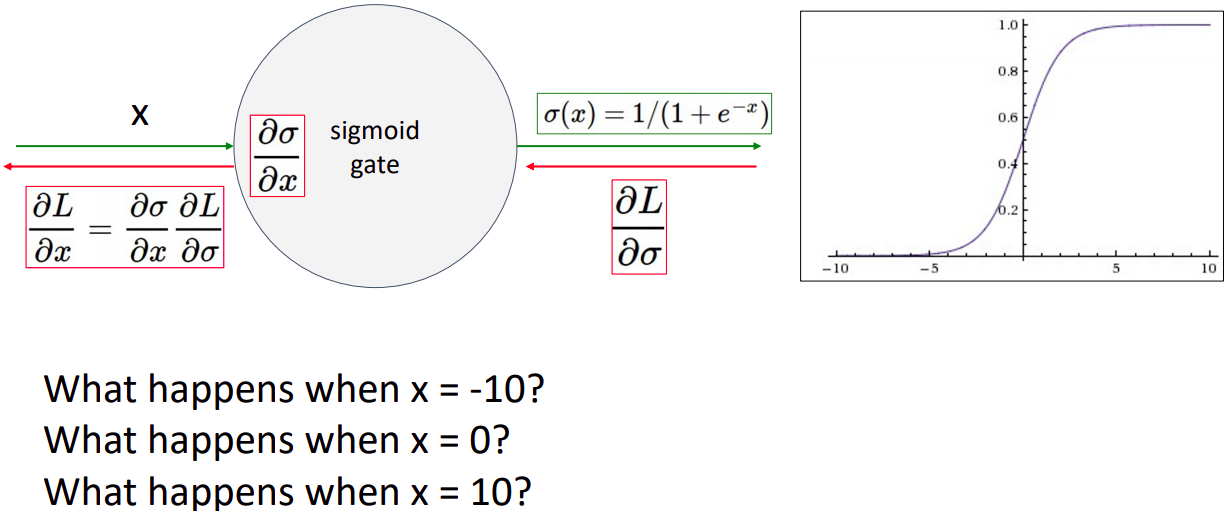
- x축의 극단 값의 gradient가 0에 수렴하므로 근본적으로 학습에 어려움을 갖고 있다.
local gradient: 값이 0에 수렴하게되고 down stream gradient값은 (upstream gradient값이 무엇이던지) 마찬가지로 0에 수렴하게 된다. 따라서 학습과정이 굉장히 느리게 진행되며 깊은 네트워크 학습에 어려움이 있다.(특정 레이어가 극단 값을 가진다면 이후에 연결된 레이어는 gradient가 업데이트가 거의 되지 않기 때문)

- Sigmoid의 결과 값이 항상 양수값을 갖고있음으로(0~1사이의 값을 가짐) 위 그림에서 W값의 gradient를 계산할 때, local gradient값은 항상 양수이며, upstream gradient값이 음수인지 양수인지에 따라 모든의 gradient값이 항상 음수나 양수로 고정된다.
- 오른쪽의 그림을 예시로 들면, Weight인 W1과 W2의 좌표계에서 파란색의 직선이 최적의 W벡터이다. gradient의 업데이트 방향이 빨간색으로 진행되는데 허용된 update벡터는 초록색사분면인 모두 음수인 경우와 양수인 경우이다. 따라서 업데이트시 지그재그 방향으로 업데이트 되는 것을 볼 수 있다. 예시로는 2차원의 W값이지만 실제로는 D차원의 평면일때 Update가 최적의 방향이 일 때 굉장히 많은 수의 지그재그 움직임으로 맞춰야 하기 때문이다.
- 다행히 minibatch에서의 평균을 구하므로 single element보다 상황은 나아진다.

- CPU계산시 지수함수 계산상 많은 clock cycles이 소모되며, 개인적으로 실험했을때 relu에 비하여 약 3배정도 느리다고한다.
Activation Functions: Tanh

- sigmoid의 scaled & shifted version으로 매우 큰값과 작은 값에서 gradient가 0이된다.
- 출력값의 중심이 0으로, sigmoid에서의 지그재그로 업데이트되는 문제는 해결되었다.
Activation Functions: ReLU

- input값이 positive일 경우 saturate(0에 수렴)되는 일이 없다.
- 연산부하가 상대적으로 굉장히 가볍다.
- sigmoid와 같이 출력값이 항상 0 혹은 양의 값을 가지지만, (제가 생각하기에 다른 장점으로 인해 학습이 어려움없이 진행됨에따라) sigmoid애서의 문제보다는 크게 걱정할 것이 아니라고 합니다.
- 입력값이 0미만일 경우 local gradient값이 0이되므로 sigmoid보다(gradient가 0보다는 약간 크기때문) downstream gradient가 완전히 죽는(0이됨)경우가 발생한다.
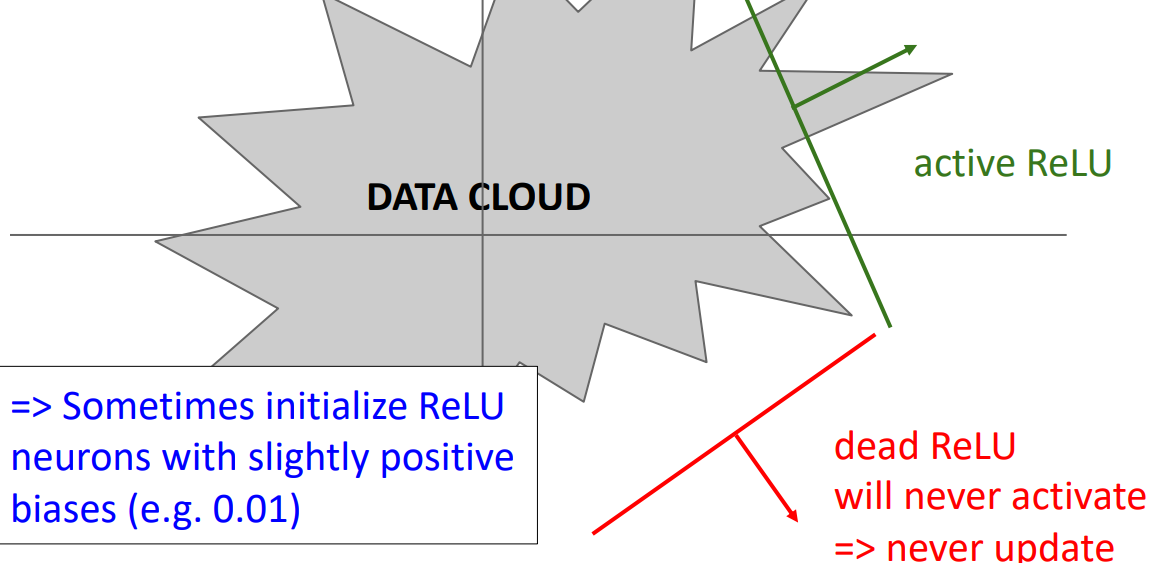
- dead ReLU:
- 상황: 학습시 모든 data point에서 negative activation값을 가질 경우, 해당하는 layer의 weiht의 gradient가 항상 0이된다. 따라서 전혀 업데이트 되지 않는다.
- 해결: ReLU의 초기 bias를 설정하여, 약간의 양수값을 가지게 만듦으로 0이 되는 것을 방지한다.
Activation Functions: Leaky ReLU

- zero-centered output과 음수인 값에서 gradient가 0이되는 것을 보완했다.
- sigmoid와 ReLU와 달리 죽는 경우가 없다. local gradient가 0이 되지 않기 때문이다.
- 음수값에서의 기울기 값도 hyperparameter이기 때문에 설정하는데 어려움과 번거로움 있다.
Activation Functions: PReLU
- Leaky ReLU에서의 기울기 값을 parameter으로 설정하여 학습중에 알아내도록 설정했다.
Activation Functions: ELU

- 장점
- ReLU의 단점인 zero-centered output을 시도했다.
- 단점
- 음의 극단 값에서 gradient가 0에 수렴한다.
- 지수함수이기 때문에 연산량이 많다.
Activation Functions: SELU
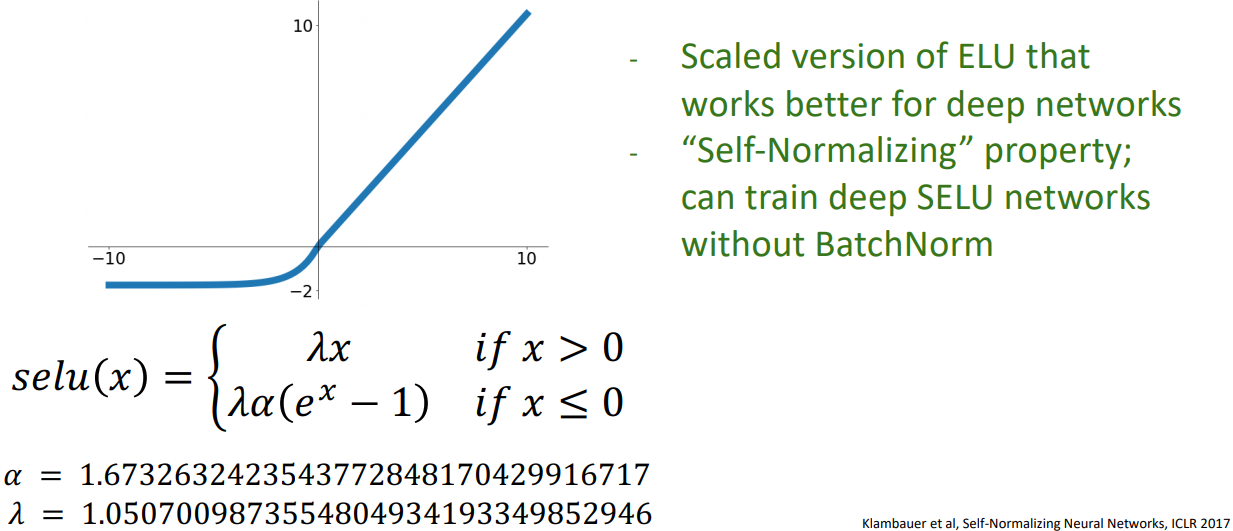
- scale한 버전의 ELU이다.
- 알파와 람다를 매우 특별한 값으로 설정한다면, 매우 깊은 네트워크에서 두 parameter가 self-normalizing특성을 가지게 된다. 따라서 BatchNorm없이 학습이 가능하다. (논문의 derivate만 91페이지라고 한다..)
Activation Functions: GELU
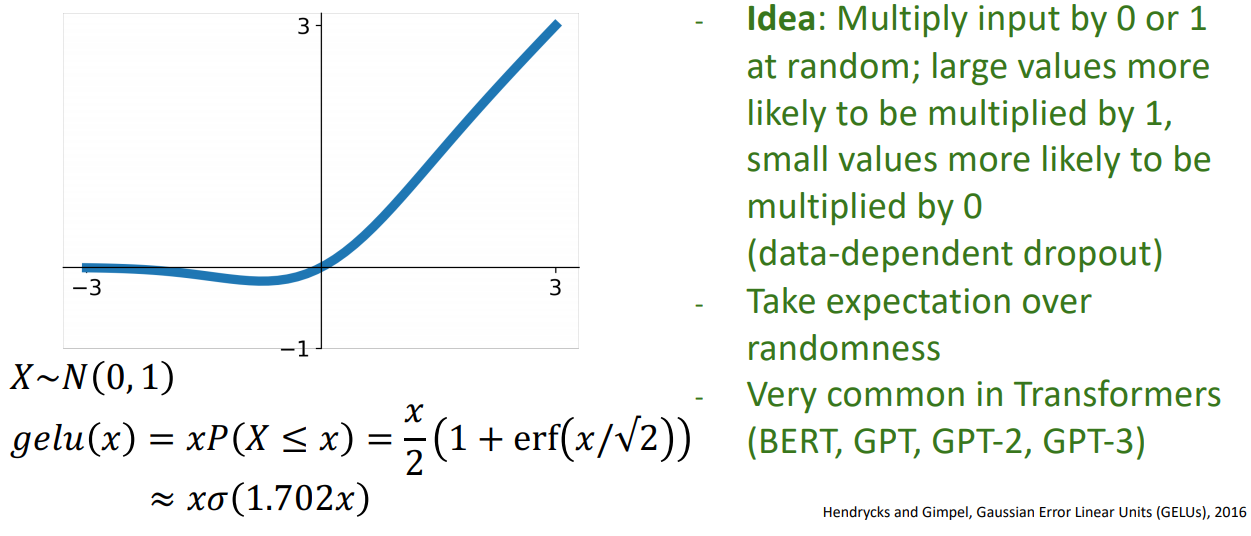
- 입력값에다가 입력값의 standard Gaussian cumulative distribution function:을 곱한 것으로 이 된다.
- 상대적으로 큰값의 경우 1에 가까운 값을 곱하게 되며, 작은 값의 경우 0에 가까운 값이 곱해진다. 입력값의 상대적인 크기에 따라 가중치가 부여된다.(data-dependent dropout)
- ReLU 및 ELU보다, 양의 영역에서 not linear하며 모든지점에서 curvature을 이루기 때문에 복잡한 기능을 쉽게 접근 할 수 있다고 합니다.
- 학습 팁으로는 모멘텀이이 있는 optimizer를 선택하고, Gaussian distribution의 누적 함수 분포(cumulative distribution function)에 근사를 사용하라고 권하고 있다. (주로 batch-norm이후에 출력값이 정규 분포 형태를 띄고 있음으로)
Activation Functions:Summary
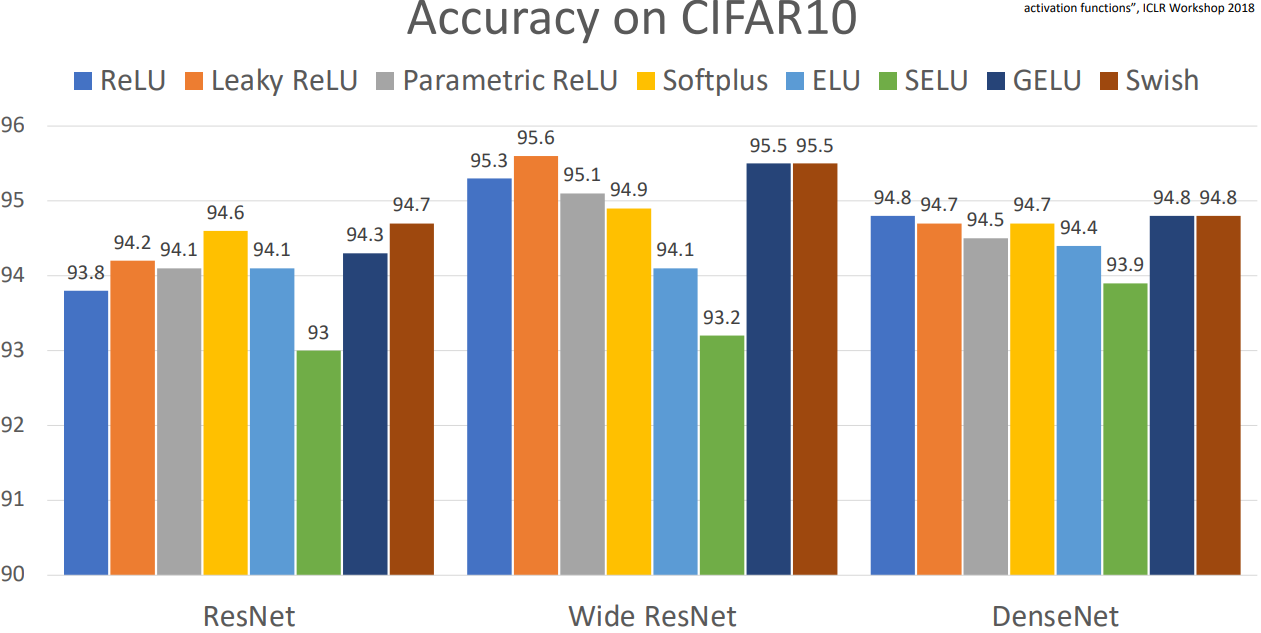
- 모델 아키텍쳐, 데이터 구성, hyper-param 구성에 따라 약간의 차이가 있어, 초기 ReLU 사용을 권한다.
- Leaky ReLU / ELU / SELU / GELU 의 선택지는 마지막 0.1%를 위해 선택하자.
- Don’t use sigmoid or tanh
Data Preprocessing
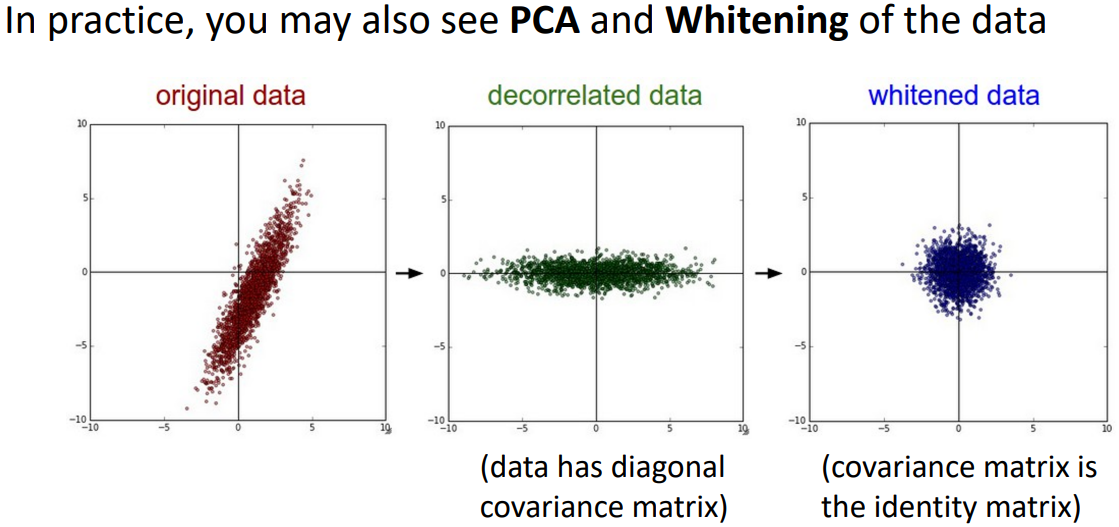
- 이미지 데이터의 경우 대부분 입력값에 평균값을 빼고 표준편차값을 나눠 줌으로 Data Preprocessing을 한다.(Normalize)
- 이미지 데이터가 아닐경우, 전체 학습 data에서 covariance matrix(공분산행렬)을 구할 수 있을때, feature가 uncorrelated되게 변환(초록)할 수 있다. decorrelated이후 표준 정규 분포(평균0,분산1)이 되도록 변환(파랑)할 수 있다.
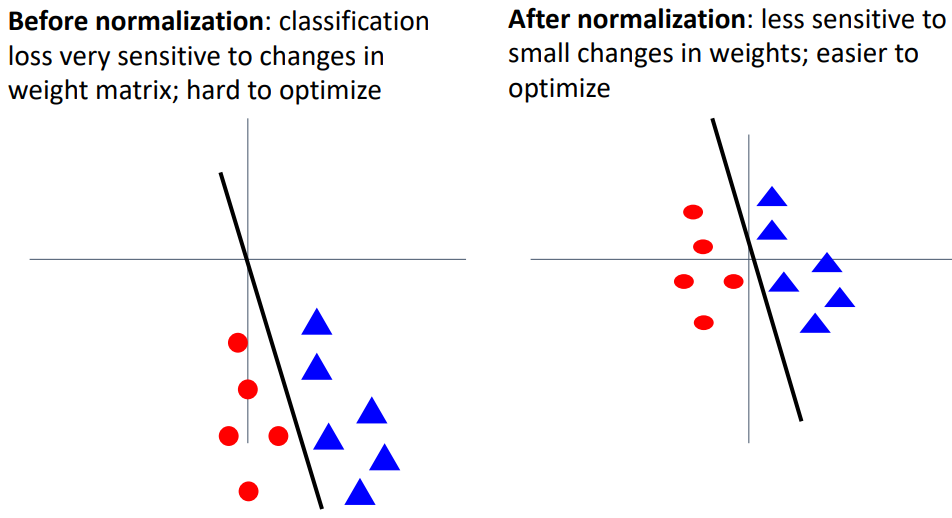
- 전처리 작업을 해준것과 안해준것의 차이는, weight의 변화에 따라 로스값의 민감도가 커지기 때문에 최적화하기에 상대적 어려움이 있다.
- CIFAR-10의 [32,32,3] images를 어떻게 전처리 했는지 모델별로 확인해보자.
- Subtract the mean image (e.g. AlexNet)
(mean image = [32,32,3] array) - Subtract per-channel mean (e.g. VGGNet)
(mean along each channel = 3 numbers) - Subtract per-channel mean and Divide by per-channel std (e.g. ResNet)
(mean along each channel = 3 numbers)
- Subtract the mean image (e.g. AlexNet)
- PCA나 whitening은 일반적으로 이미지 데이터에서 수행하지 않는다.
Weight Initialization
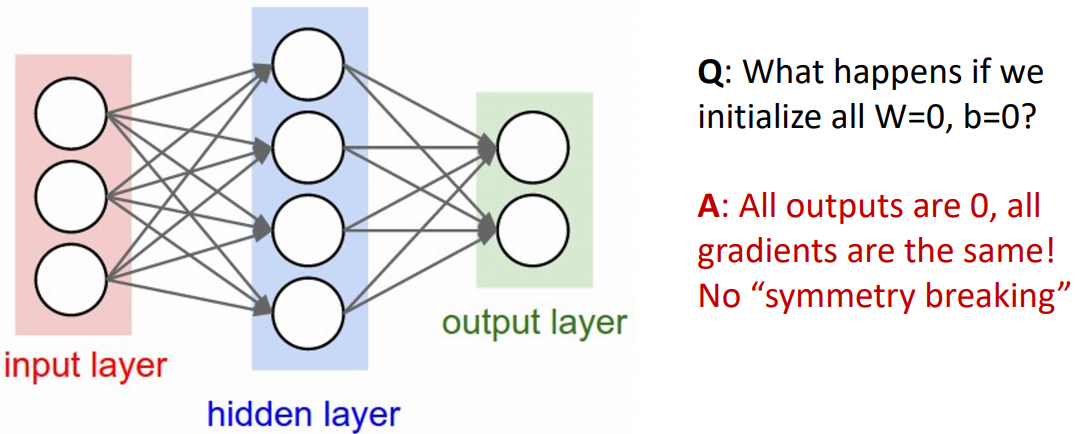
- Q: 네트워크의 모든 Weight와 bias가 0으로 초기화되면 어떻게 될까?
A: 결과값이 입력값에 상관없이 0이 되며, gradient도 0이 된다. 따라서 학습이 안 된다.
이를 symmetry breaking이 일어나지 않았다라고 한다. 학습 데이터셋에서 결과와 심지어 중간레이어의 결과 차이가 나타나지 않았기 때문이다. - constant Initialization에서 주의가 필요하다.

- 위 문제를 해결하기위해, 작은 수를 가우시안 분포에 곱하면, 얕은 네트워크는 동작하지만 깊을때 잘 동작하지 않는다.
Weight Initialization: Activation Statistics
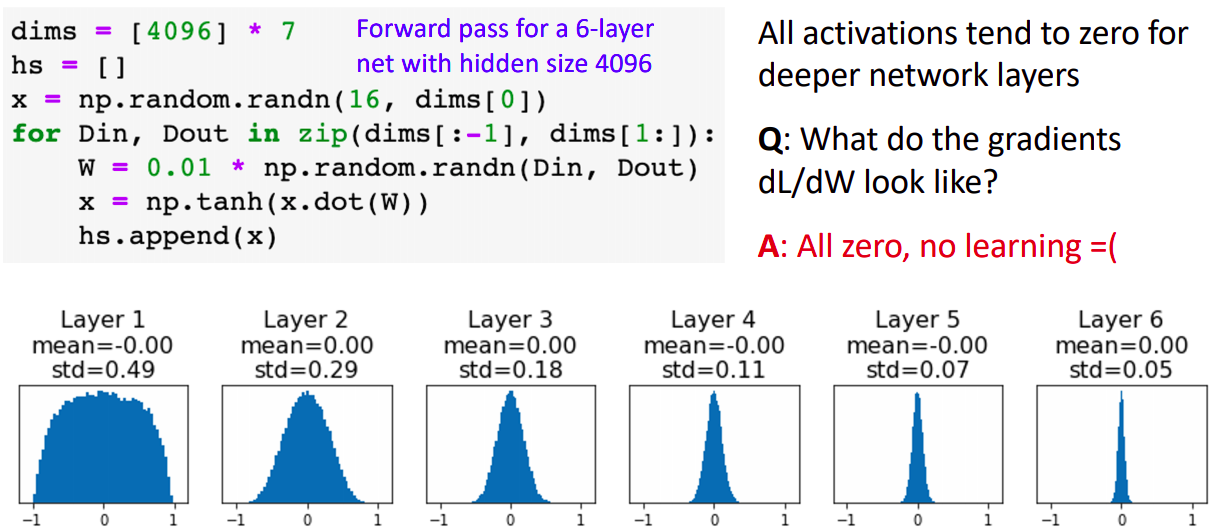
- 하단의 분포는 6계층의 레이어를 두고 각 레이어의 activation값을 plot한 결과이다.
- 초기 레이어의 경우 activation값의 분포가 잘 형성되지만 갈수록 값이 0에 collapse된다.
- 이는 weight의 gradient값이 0에 수렴하게 되고(local gradient값은 activation값 이므로) 학습진행이 잘 되지 않게된다.
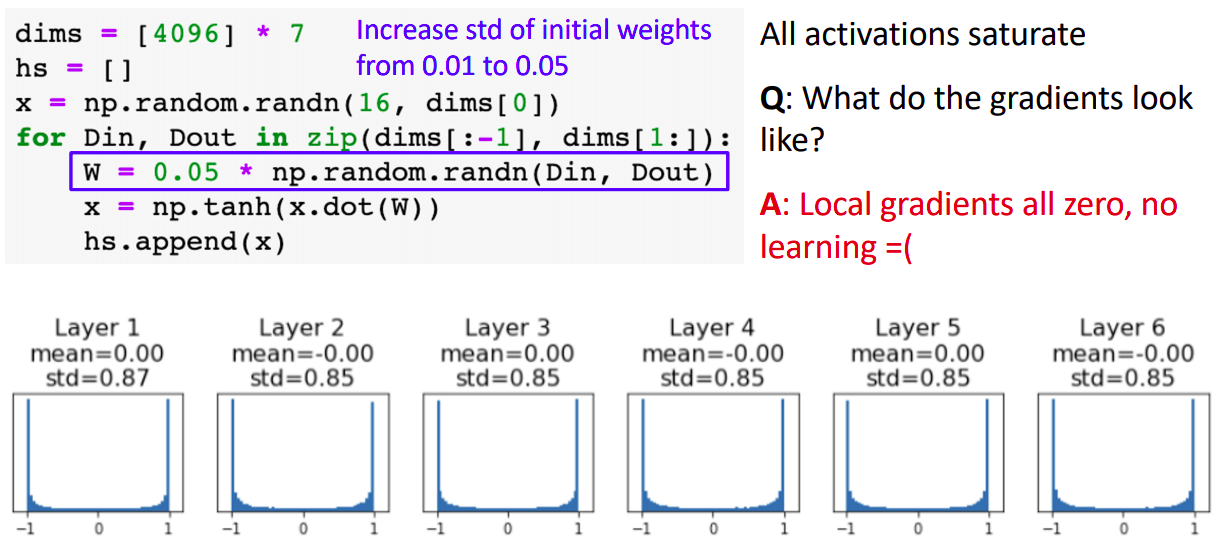
- 그렇다면 weight 값을 크게 하면 어떨까(std가 0.01에서 0.05으로)
- tanh 방식을 적용했을때 activation값이 -1과 1으로 saturated됨을 볼 수 있다(w값이 커서 wx의 값이 굉장히 크거나 작게됨). tanh의 local gradient값이 0에 수렴하게 되어 마찬가지로 학습이 어렵다.
Weight Initialization: Xavier Initialization
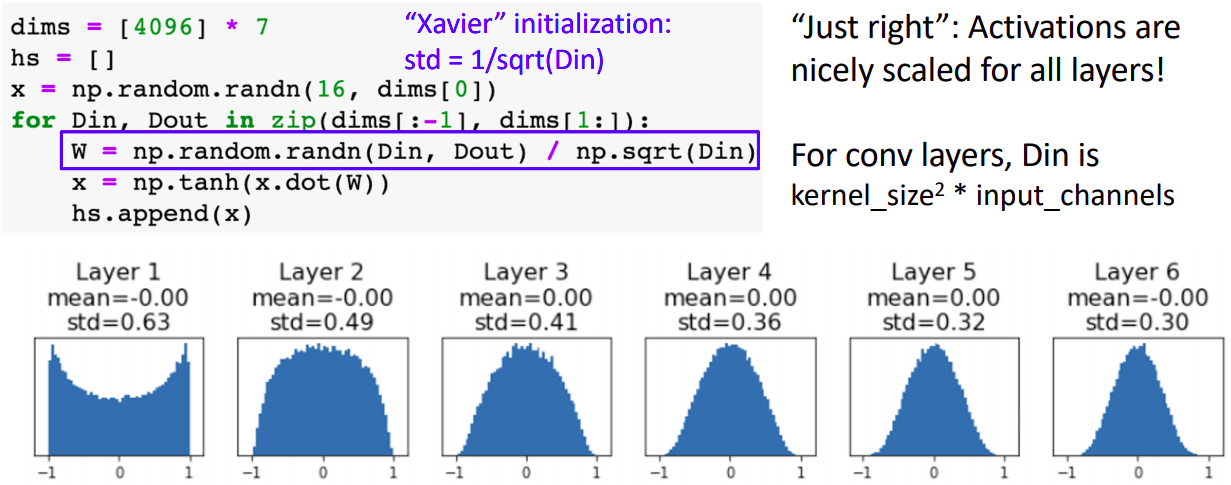
- std값을 hyperparameter으로 설정하지 않고 1/sqrt(Din)으로하면 activation값의 분포가 적절하게 설정됨을 볼 수 있다.

- Xavier initialization의 의도는 output의 variance와 input의 variance가 같게하는 것이다.
- x와 w가 independent and identically distributed라는 가정, 상호 independent random variable이며, 0을 평균을 가정한다.
- 이럴때 w의 variance가 1/Din 이면 y와 x의 variance가 같음을 유도할 수 있다.
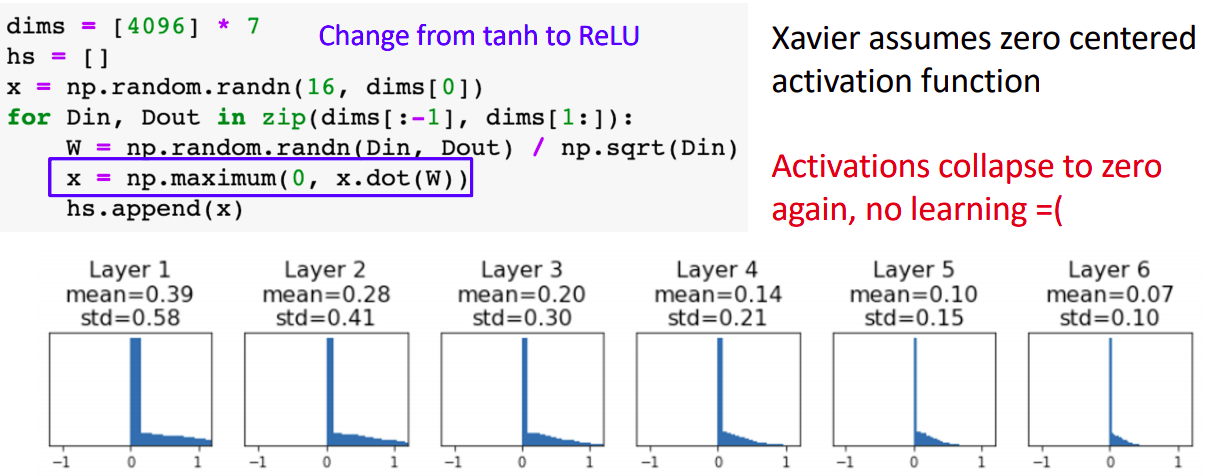
- ReLU에서는 activation 값이 0으로 collapse하며 local gradeint가 0이 되어 학습이 진행되지 않는다.
- Xavier는 x와 w가 zero-mean임을 가정하고 진행하는데, x가 zero-centered되지 않은 상태이다.
Weight Initialization: Kaiming / MSRA Initialization

- Relu input의 반이 없어지기 때문에 std값을 sqrt(1/Din) 대신 sqrt(2/Din)으로 설정했다.
Weight Initialization: Residual Networks

- P: Residual Networks에서는 입력값의 variance보다 출력값의 variance가 큰데, 이는 단순히 입력값을 출력값에 더해주기 때문이다.
- S: 첫번째 CONV를 MSRA으로 초기화 하고, 두번째 CONV를 0으로 한다면 입력값과 출력값의 Variance를 맞출 수 있다.
Regularization
Regularization: Add term to the loss
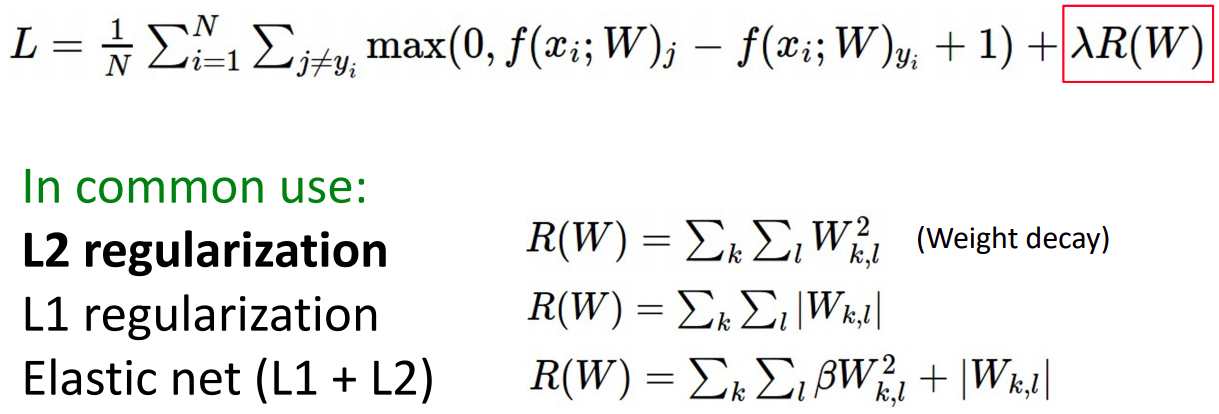
- loss 함수에 Regularization인자를 추가하여 구현했었다. L2 regularizaion을 보통 weight decay라고 한다.
Regularization: Dropout
- forward pass 도중, 랜덤하게 특정 뉴런을 제외 시키는 것으로 보통 0.5를 hyperparameter으로 설정한다.
Regularization: Dropout First interpretation

- Network이 redundant 표현을 갖게 만든다; feature에 대한 co-adaptation를 막는 용도이다.
- 판단에 있어 일부 feature를 의도적으로 배제하여 robust한 인식을 만들기 위한 목적이다.
Regularization: Dropout Second interpretation
- 큰 ensemble모델(파라미터 공유)을 학습하기 위한용도이다.
- dropout하기 전의 original network의 일부를 dropout하여 subnetwork를 생성한다. 그리고 상당한 갯수의 subnetwork(파라미터 공유)를 학습하여 original network는 subnetwork들의 ensemble한 결과이다.
Regularization: Dropout Test Time
- 입력값과 더불어 Random mask에 따라 output값이 랜덤하게 나타남으로 random variable(z)을 "average out"하는 것이다.
- 이때 z에 대하여 적분을 수행하는데 굉장히 어렵고 어떻게 하는지 모른다.

- 따라서 적분하는 대신, test time에서 뉴런을 drop하지 않고 나타날 수 있는 dropout 확률 만큼 곱한다.
Regularization: Dropout “Inverted dropout”

- test time에서의 효율성을 위해, 확률을 곱하는 rescale과정을 test time에 하지 않고, train time에 적용할 수 있다.
Regularization: Dropout Dropout architectures

- 초기 AlexNet과 VGG에서 FC leyer는 Dropout이 적용되었지만, 후기 모델에서는 FC layer대신 global average pooling을 사용하여 dropout을 전혀사용하지 않았다.
Regularization: A common pattern

- 일반적인 형태의 Regularization은 학습시에 랜덤성을 추가하고, 테스팅때 랜덤성을 종합한다.
- 최근의 Regularization은 L2와 Batch Norm을 사용한다.
Regularization: Data Augmentation
Data Augmentation: Horizontal Flips
- 좌우 대칭
Data Augmentation: Random Crops and Scales

- 학습:
- 랜덤한 사이즈 L을 고른다.
- 학습이미지의 짧은 부분이 L이 되도록 이미지를 조정한다.
- 랜덤한 부분을 224 x 224크기로 고른다.
- 테스팅:
- 5가지의 scaling 크기로 조정한다.
- 각 사이즈에 대하여 (4개의 코너사진 + 1개의 중앙사진) x (대칭사진 2)만큼의 이미지의 결과를 종합하여 나타낸다.
Data Augmentation: Color Jitter
Regularization: DropConnect
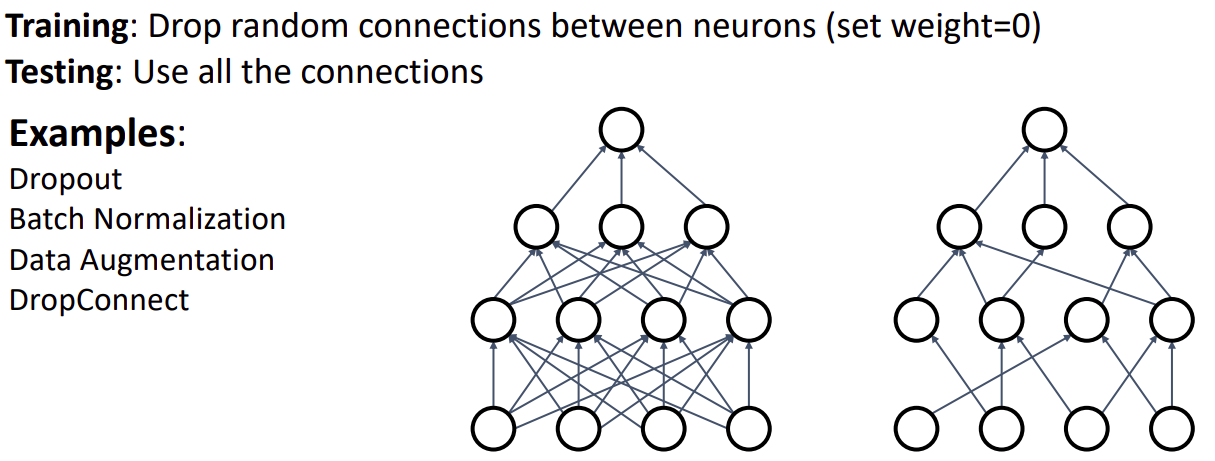
- 랜덤하게 뉴런의 activaiton값을 0으로하는 대신, weight를 0으로 한다.
Regularization: Fractional Pooling
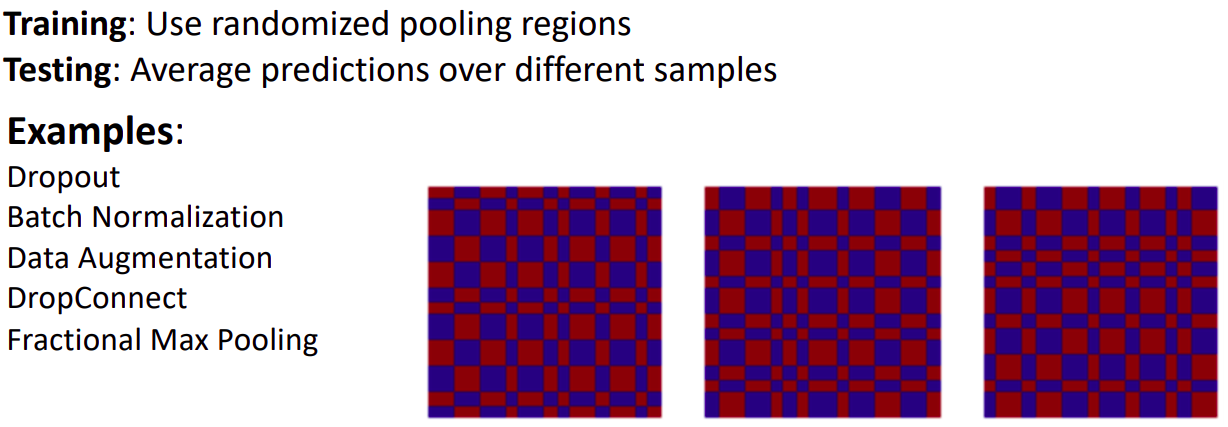
- pooling region인 receptive field크기를 랜덤하게 설정한다.
Regularization: Stochastic Depth

- 랜덤한 Residual block을 drop한다.
Regularization: Cutout

- 랜덤한 이미지 region을 0으로 한다.
Regularization: Mixup

- 이미지들을 blend weight에 따라 blend 한다. label은 blend weight이다.
- blend weight는 beta 분포으로 사실상 0과 1에 가깝다.
Regularization: Summary

- dropout은 매우 큰 FC 레이어 외에는 사용하지 않는다.
- BN과 data aug는 항상 좋은 선택이다.
- 작은 데이터셋의 경우 cutout과 mixup을 시도해 보자.
참고자료
cs231n 강의 자료
cs231n 한글 강의 자료
EECS 498-007 / 598-005 2019 강의 자료
