자율주행 제어에 있어서 유명한 횡방향 제어 기법 중 하나인 Stanley method에 대해 총 정리를 하고자 합니다.
PID로 조향각을 제어해 보았지만, 게인 튜닝에 머리가 깨질 것 같은 고통을 느끼고 자율주행에서 훨씬 많이 쓰이고 유명한 Stanley method의 필요성을 절실히 실감하여, 공부하고 정리하였습니다.
Stanley Method 컨셉
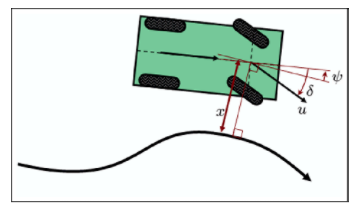
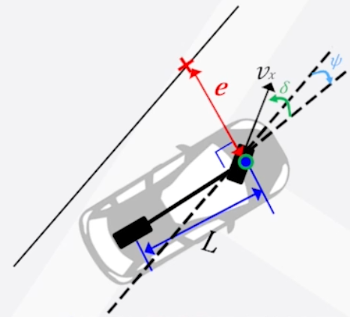
Stanley method (SM)은 따라가고자 하는 1) 차선의 곡률과, 2) 횡방향 오차()를 사용하여 차량의 조향각을 제어하는 방식입니다.
- : 조향각 (steering angle)
- : 현재 차량의 Yaw값과 차선의 곡률 각도와의 차이 각
ex) 위 그림에서 차선의 곡률 각도: -15˚, 현재 차량의 Yaw: -5˚ -> - : Gain 값, 임의로 지정 가능
- : 횡방향 오차, 현재 추종하는 차선의 중심 위치와 차량의 앞바퀴 사이의 최단 거리.
※중요※ 즉, 차선과 앞바퀴 좌표(A)와, 앞바퀴와 최단거리인 차선의 좌표(B) 사이 직선은 B좌표에서의 곡률 각도와 수직이다 - : 차량의 종방향 속도
1) 차선의 곡률
차량의 Yaw 값과 차선의 곡률 각도가 같아야하는 것은 자명할 것입니다. 차선이 직선이라면, 차량 또한 직선으로 조향해야 할 것이며, 곡선 구간이라면, 곡선의 곡률과 같은 조향각으로 회전해야 할 것입니다.
2) 횡방향 오차
아래 그림 1과 같이 차선과 차량 사이에 횡방향 오차가 있다면 오차가 0이 되도록 주행하는 것은 자명할 것입니다. 차선이 차량의 중심에 오도록 주행해야 하므로 횡방향 오차가 0이 되도록 주행해야합니다.
Stanley’s steering controller, at the core, is based on a non-linear feedback function of the crosstrack error, for which exponential convergence can be shown.
횡방향 오차의 수식은 위의 원본 논문에서 발췌한 것과 같이 SM의 코어에 해당하는 비선형 함수로 기하급수적으로 횡방향 오차가 0으로 수렴하도록 만듭니다. 또한 k는 얼마나 빠르게 0으로 수렴할지 정해주는 파라미터로 작용합니다.
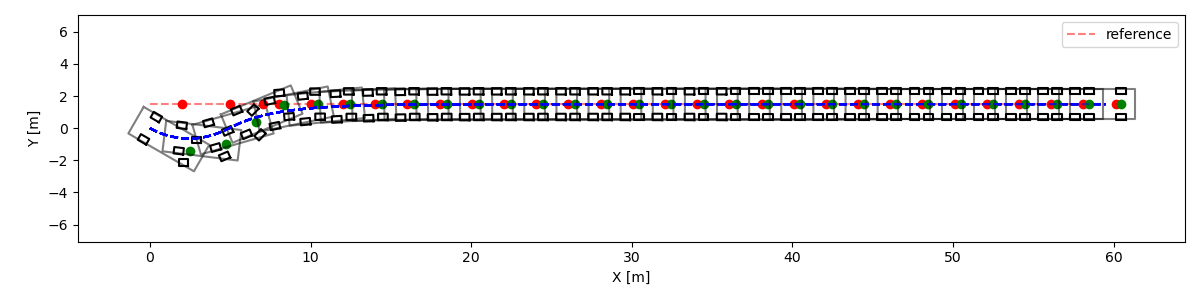
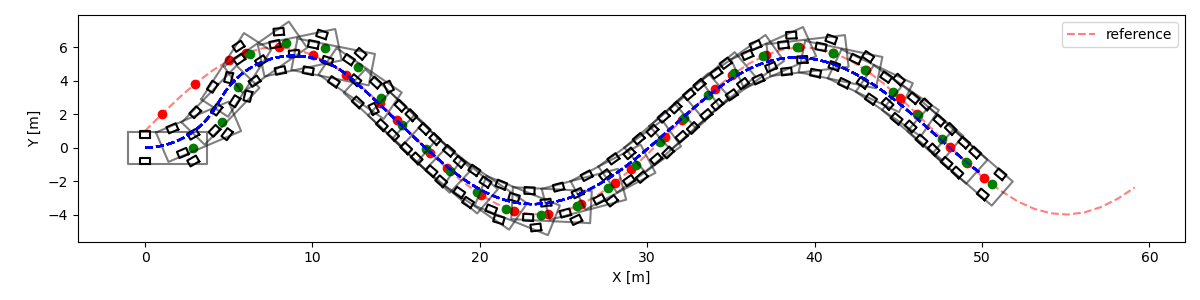
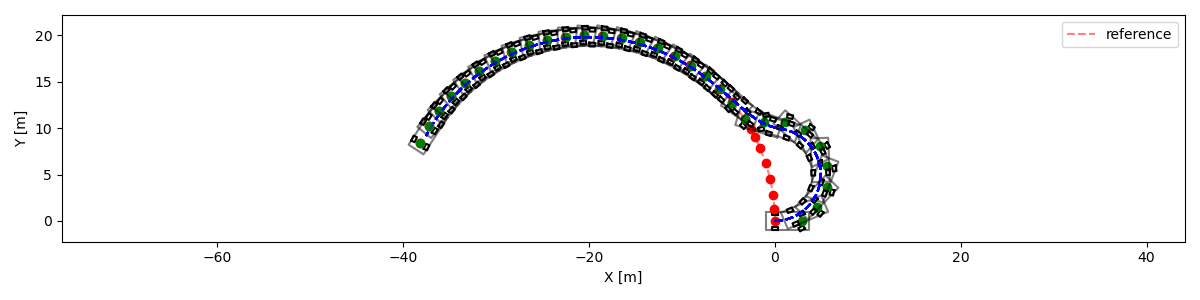
결과