미분

정의

미분(Derivative)이란 어떤 함수의 특정 지점에서의 순간적인 변화율을 이야기 한다. 함수$f(x)$가 어떤 실수 $x$에 대한 변화를 나타낸다고 할 때 $f(x)$의 미분이란 x가 아주 조금 변했을때, $f(x)$가 얼마나 변하는지를 나타내는 것이 미분이다. 쉽게 이야기 하자면, 대나무 숲에 있는 대나무가 지난 얼마만큼의 기간 동안 얼마만큼 자랐으니 다음 기간동안엔 얼마나 자랄까? 라는 문제에 대해 해결방법을 찾는 것이다. 이 문제에 대해 "대충 일주일동안 1미터 자랐으니 다음 1주일동안 1미터 자라겠지..."라는 정도로 게으른 예측을 할 수도 있겠지만 이럴 경우 시간($\Delta x$)이 대나무에 생장에 대해 얼마나 영향을 미치는지 정확히 파악하고 해설 할 수가 없다. 미분은 이런 문제에 대해 순간적인 변화를 찾아 낸다. 일주일의 데이터로 일주일을 예측하는 것보다 하루치 데이터로 하루를 예측하는 것이 더 정확할 것이기 때문에 한시간, 분, 초, 밀리초 단위... 이처럼 연속된 값을 한없이 0에 가까운 순간으로 확대해서 자르고 그 다음 지점에 대한 변화율(기울기)값을 구하는 것이 미분이다. (내생각은... 한 없이 작은 순간의 시간이 대나무의 성장에 대해 미치는 영향을 최대한 정확하게 파악하여 상수로 둔다면, 대나무의 성장에 영향을 미치는 다른 요소들에 대해 파악하고 조정하는데 도움이 될것 같다.)

Formula

$f\prime(x) = \lim_{\Delta{x\to0}}\frac{f(x+{\Delta{x}})-f(x)}{\Delta{x}}$

• $f\prime(x)$ : 함수$f(x)$의 도함수(에프 프라임 엑스라고 읽는 듯...) 순간적인 변화율, 즉 기울기 값을 의미한다.
• $\lim_{\Delta{x\to0}}$ : 변화를 유발하는 $\Delta{x}$ 가 연속적으로 0에 무한히 가까워 질 때의 한계를 의미한다.
• $\frac{f(x+{\Delta{x}})-f(x)}{\Delta{x}}$ : x에서 $\Delta{x}$까지 함수 $f(x)$의 평균 변화율을 나타낸다.

거듭제곱 법칙의 적용

함수 $f(x)=x^n$(n은 실수) 의 형태일 때 곱셈공식에 의해 $f(x+{\Delta{x}})$는 $x^n+nx^{n-1}\Delta{x}+더 높은 차수의 항들$로 전개가 된다. 이후로,

• 도함수는 $f\prime(x)=\frac{(x^n+nx^{n-1}\Delta{x}+더 높은 차수의 항들)-x^n}{x^n}$이된다.
• $x^n$은 상쇄되어 사라지고, $f\prime(x)=x^n+nx^{n-1}\Delta{x}+더 높은 차수의 항들$ 의 형태가 된다.
• $\Delta{x}$가 0으로 접근할 때 $\Delta{x}$를 포함하는 항들이 $\Delta{x}$로 나뉘어지면서 $nx^{n-1}$ 의 항만 남게 되고, 나머지 항은 사라진다. (극한의 정의에 대해서도 공부를 해야할듯 하다)
• 따라서 $f\prime(x)= nx^{n-1}$의 형태가 된다.

한마디로

함수 $f(x)=x^n$의(n은 실수) 도함수를 구하기 위해서 $f\prime(x)= nx^{n-1}$ 으로 계수를 내리고 지수를 $-1$ 한다.

• $f(x)= x^2$의 경우, 도함수는 $f\prime(x)= 2x^{2-1} = 2x$
• $f(x)= x^3$의 경우, 도함수는 $f\prime(x)= 3x^{3-1} = 3x^2$
• $f(x)= x^4$의 경우, 도함수는 $f\prime(x)= 4x^{4-1} = 4x^3$
• $f(x)= x^5$의 경우, 도함수는 $f\prime(x)= 5x^{5-1} = 5x^4$

조금더 정리하면...

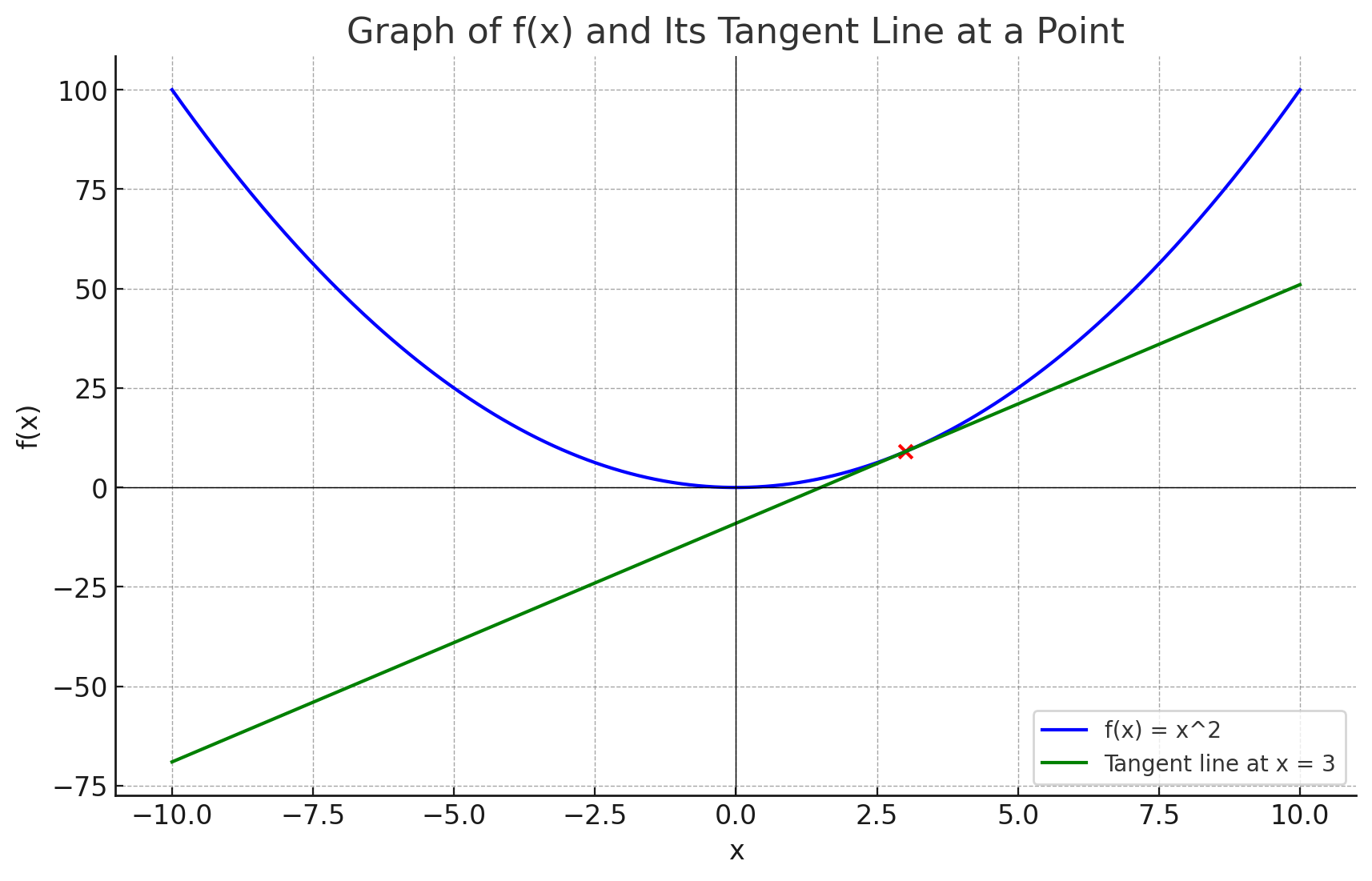
• 파란색 곡선 : $f(x)=x^2$의 그래프로 $x=0$일때 최소값은 0이다
• 빨간색 X : $x$가 3일경우 $f(3) = 3^2 = 9$를 나타내는 점으로 함수의 그래프와 접선이 만나는 지점이다.
• 녹색 직선 : 접선으로써 $x=3$일때의 그 순간의 기울기(변화율)을 나타낸다. $f(3) = 3^2 = 9$ 일때 $f\prime(3) = 3 * 2 = 6$ 이다. ($x=3$일때의 기울기는 $y=6(x-3)+9$로, $y=6x-9$가 된다.)