
해당 포스트는 패스트 캠퍼스에 초격차 패키지 : 50개 프로젝트로 완벽하게 끝내는 머신러닝 SIGNATURE를 공부한 뒤 복습을 위해 각색하여 작성하였습니다.
01. 시작하며
이번 17번째 미니 프로젝트에서는 많은 분들이 아시는 사이킷런의 Boston 부동산 데이터를 사용하여 가격 예측 실습을 진행했습니다.
이전 미니 프로젝트들에서 했던 것처럼 모델링을 하는 것도 중요하지만, 모델링 이후 해석을 하는 것도 매우 중요했습니다. 특히나 집값 혹은 재산 등을 예측할 때는 explainable, 설명이 가능한 모델을 활용하여 예측 및 분석을 하는 것이 유용하다고 합니다.
그래서 이번 실습에서는 직관적으로 해석이 가능한 모델인 Decision Tree와 Linear Regression을 활용하여 Boston 집값 예측 및 해석을 진행했습니다.
먼저 전체 데이터에 대하여 모델링을 한뒤, 상위 60%와 하위 40%의 집값 분포의 차이점을 분석 및 모델링을 했습니다. 이때 Regression 문제를 Classification 문제로 변형을 했습니다.
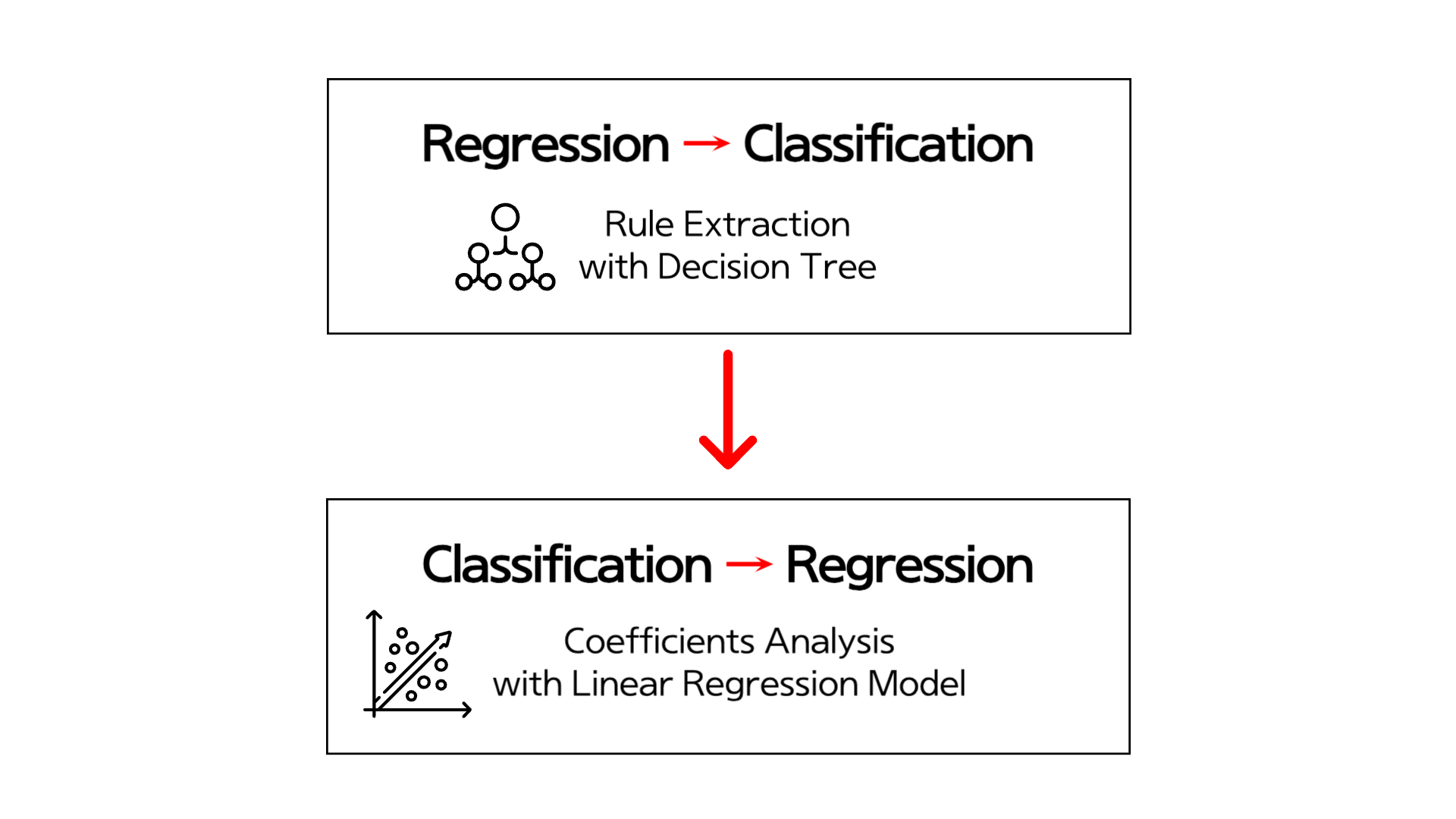
Classification 문제 (상위 60% → class 1, 하위 40% → class 0)으로 변형 한 후 Decision Tree 모델을 활용하여 node들을 보며 모델을 해석했습니다.
이후 다시 Regression 문제로 변형했습니다. 다시 Regression으로 바꿀 때는 상위 60%와 하위 40%의 데이터 분포를 따로 모델링하여 Linear Regression 모델의 계수를 통해 1단위가 바뀔 때마다 계수가 어떻게 바뀌는지 분석했습니다.
이후 챕터에서 해당 과정을 더 자세히 알려드리겠습니다! (이전 미니 프로젝트들에서 했던 문제해결 프로세스 정의, 데이터 확인 과정은 건너뛰었습니다!)
02. 모델링 & 해석
모델링에 사용한 변수들은 아래와 같습니다.
- CRIM: 자치시 별 1인당 범죄율
- ZN: 25,000 평방피트를 초과하는 거주지역의 비율
- INDUS: 비소매상업지역이 점유하고 있는 토지의 비율
- CHAS: 찰스강에 대한 더미변수(강의 경계에 위치한 경우는 1, 아니면 0)
- NOX: 10ppm당 농축 일산화질소
- RM: 주택 1가구당 평균 방의 개수
- AGE: 1940년 이전에 건축된 소유주택의 비율
- DIS: 5개의 보스턴 직업센터까지의 접근성 지수
- RAD: 방사형 도로까지의 접근성 지수 (도시 중심으로부터의 접근성) --> 높으면 도심
- TAX: 10000달러당 재산 세율 --> 높으면 좋은 주택을 가지고 있음
- PTRATIO: 자치시별 학생/교사 비율 --> 자치시별로 비율이 똑같은 곳이 있음을 알 수 있음.
- B: 흑인의 비율
- LSTAT: 모집단의 하위계층의 비율(%)
- MEDV: 본인 소유의 주택가격 중앙값
여기서 MEDV는 타겟값입니다.
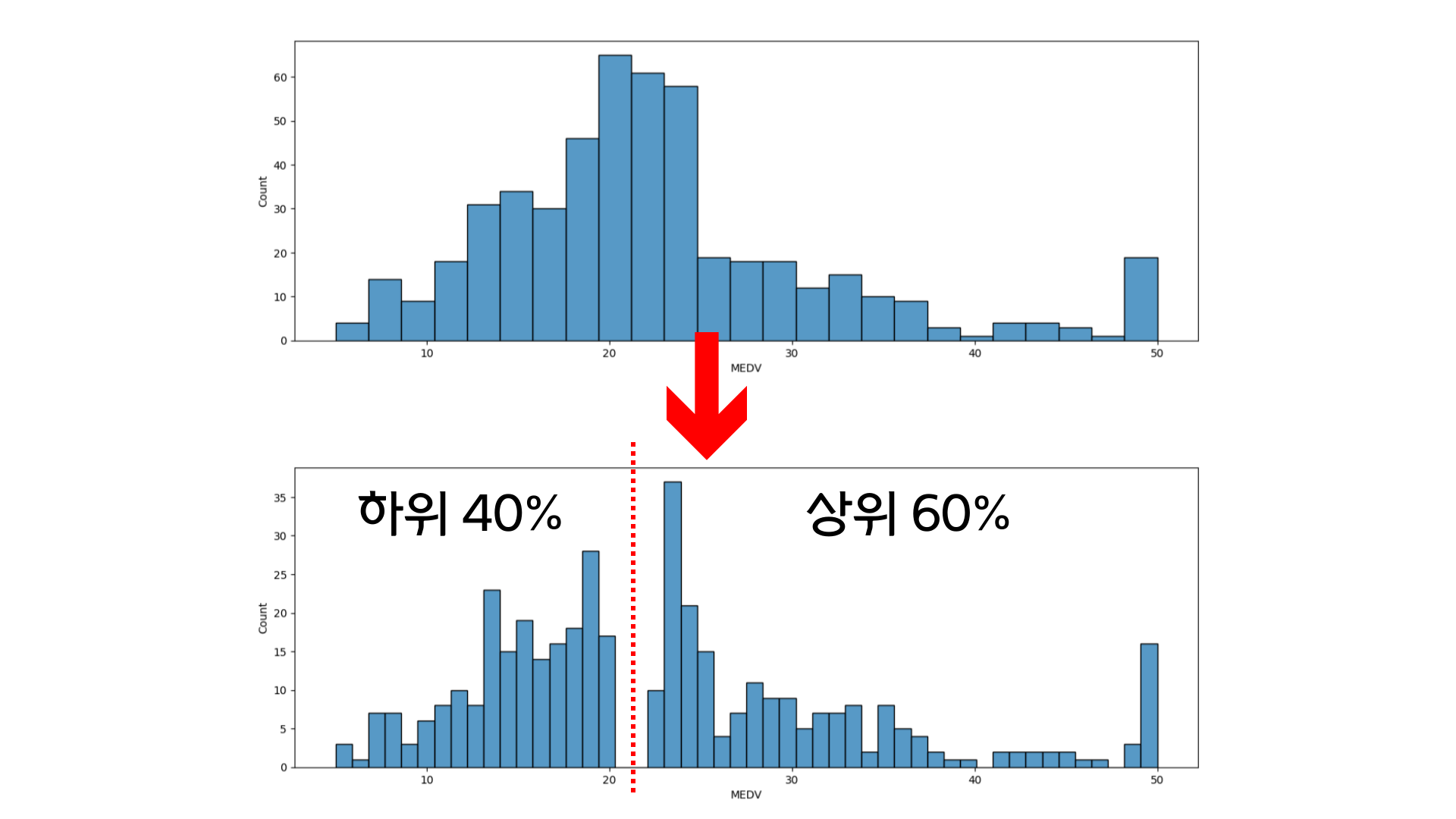
MEDV의 원래 분포는 이미지의 위의 히스토그램과 같습니다. 하지만 이번 미니 프로젝트에서 실습해보고자 했던 것은 Regression 문제를 Classification으로 나누는 것이었습니다. 그래서 np.percentile을 이용하여 하위 40%와 상위 60% 데이터를 나누었습니다. 그 결과는 이미지의 아래 히스토그램과 같습니다. 중간의 40% ~ 60%에 해당하는 데이터들은 필터링을 통해 삭제되었습니다.
데이터 분포를 나누었으니 다음으로 DecisionTreeClassifier를 사용하여 1,0 Binary Classification 모델링을 했습니다. Decision Tree 모델은 사실 현재 많은 모델들이 나와 좋은 모델은 아닐지라도 직관적으로 해석을 할 수 있다는 장점때문에 사용했습니다. max_depth 하이퍼파라미터를 조정한결과 3일때 검증 데이터셋에서 좋은 결과를 냈습니다. 시각화한 결과는 아래와 같습니다.
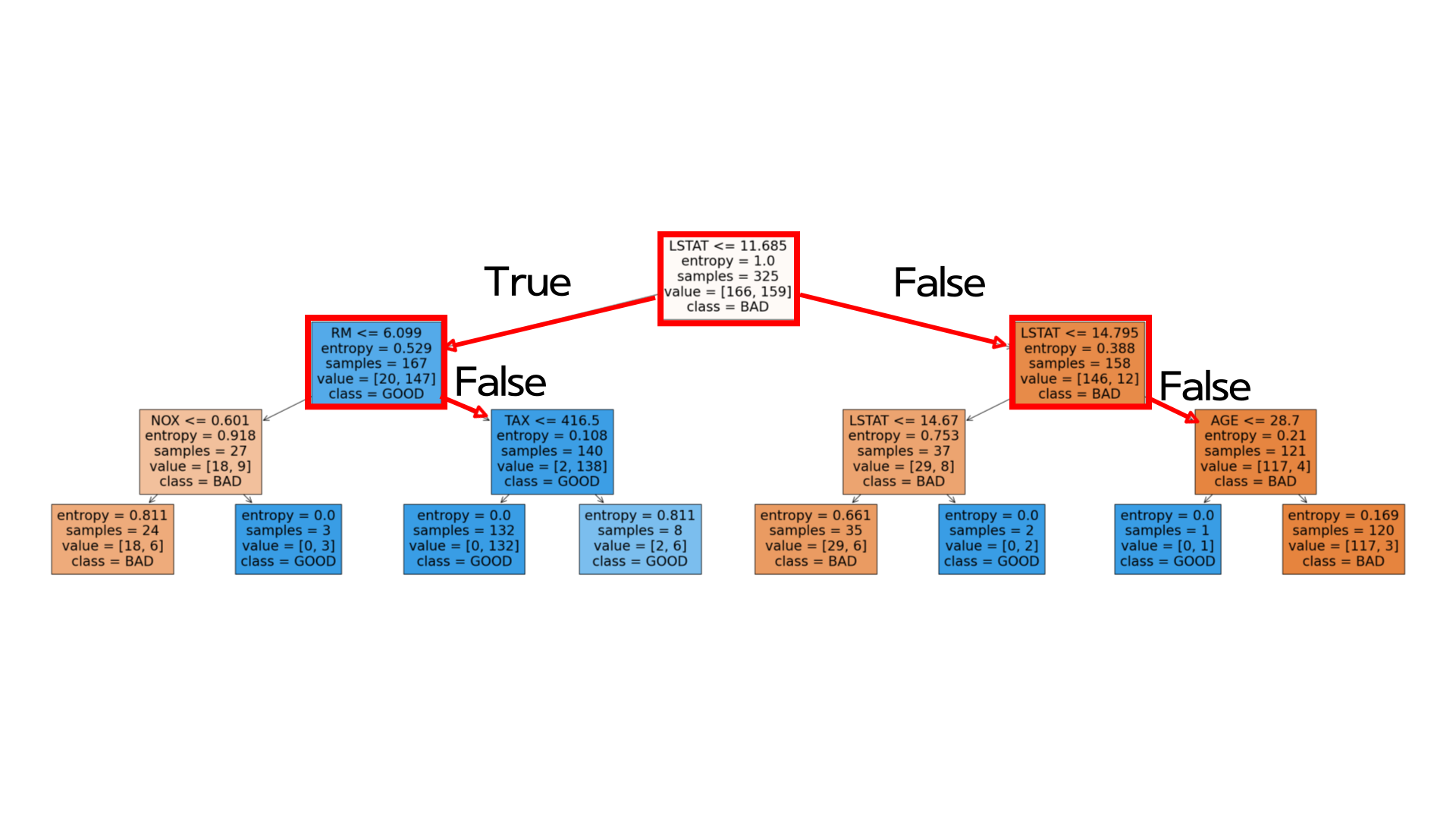
위의 트리를 해석한다면, 높은 가격대의 집값 (GOOD)과 낮은 가격대의 집값(BAD)을 나눠주는 첫번째 변수는 LSTAT (모집단의 하위계층의 비율)입니다. LSTAT는 데이터의 불순도를 제일 많이 낮춰주는 요소로, 모집단 하위 계층의 비율이 11.65%이하일 때 하위 40% 집값, 11.65%를 넘었을 때 상위 60% 집값으로 분류가 된다는 것을 알 수 있습니다.
다음 노드로 넘어가면 상위 60% 집값의 경우 RM <= 6.099이 False일 때 좋은 집값으로 분류됩니다. 종합하면 모집단 하위 계층의 비율이 11.65% 이하일 때, 방의 개수가 6개를 넘을 때 상위 60%의 집값으로 분류가 됩니다.
반대로 하위 40% 집값의 경우 LSTAT이 14.795를 넘을 때 하위 40%의 집값으로 분류됩니다. 종합하면 모집단 하위 계층의 비율이 11.68%보다 높고, 14.795%보다 높으면 하위 40%의 집값으로 분류가 되는 것을 확인할 수 있었습니다.
Decision Tree 모델링을 통해 LSTAT이 두 집단을 나누는 중요한 변수라는 것을 발견할 수 있었습니다. 그렇다면 LSTAT는 각각의 데이터 분포에서 1단위당 어떻게 변할까요? 다시 Regression 문제로 변형하여 계수를 통해 분석을 해보겠습니다.
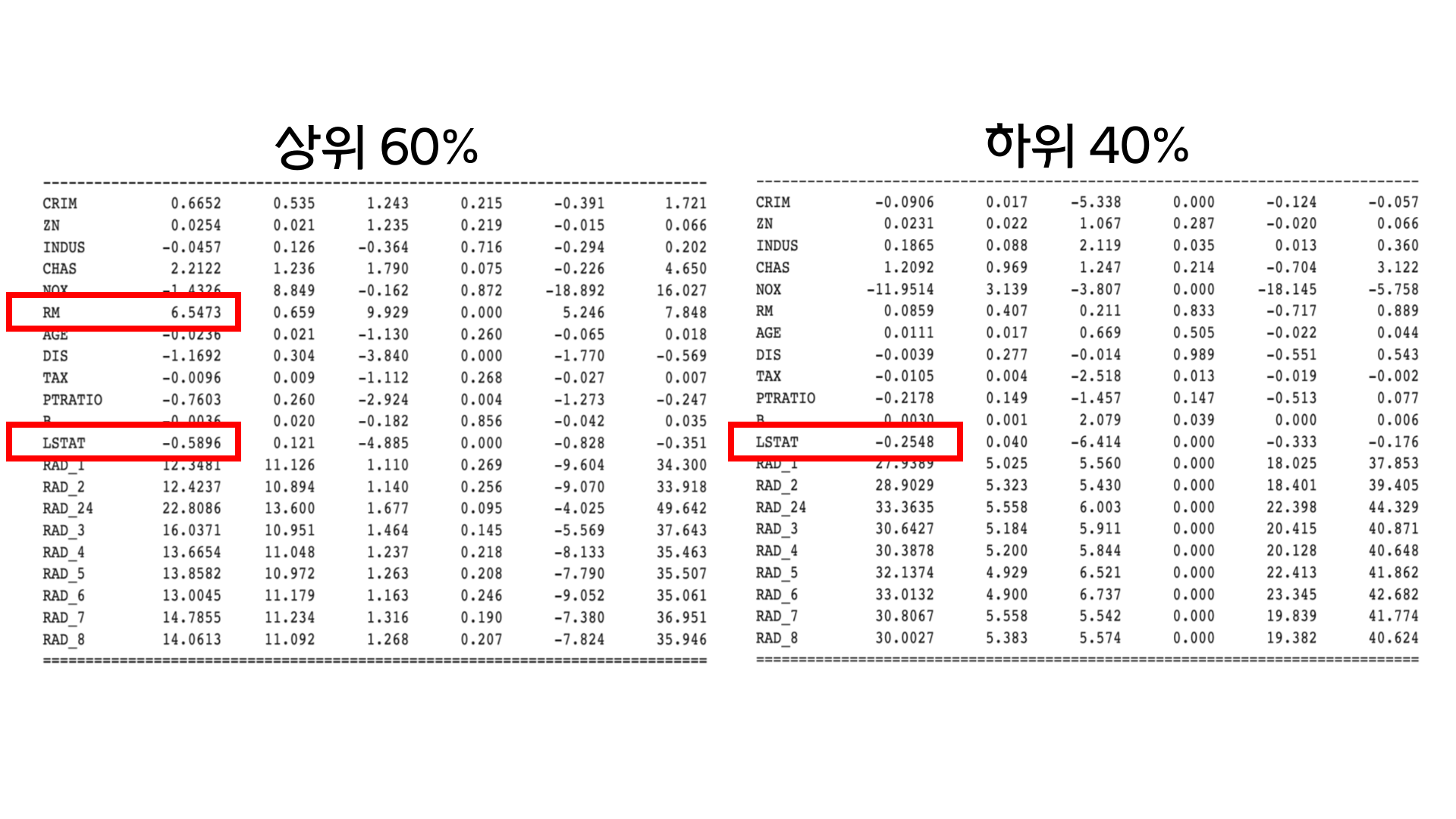
상위 60% 집값의 분포의 경우 LSTAT (모집단 하위 계층의 비율)이 1단위 증가할 때마다 약 0.59% 씩 떨어지는 것을 확인할 수 있습니다. 이는 하위 40%에서 약 0.25%가 떨어지는 것과 비교하면 두배 이상으로 많이 떨어지는 것을 알 수 있습니다.
다른 변수도 보면, 상위 60% 집값 분포의 경우 RM (방의 개수)의 경우 1단위 증가할 때마다 6.54씩 증가합니다. 반대로 하위 40% 집값 분포의 경우 약 0.09로 값이 잘 증가하지 않습니다.
03. 마무리하며
이번 실습을 통해 데이터 분석에서 중요한 해석을 어떻게 하는지 조금 더 이해하는 과정을 가졌습니다.
이전에 Boston 데이터를 활용했을 때는 feature engineering 이후 하이퍼파라미터를 조정하며 성능을 높이는 데에만 집중했었습니다.
하지만 이번에 해석을 하는 과정을 통해서 현업가들에게 분석한 모델에서 나온 결과를 어떻게 제안할 수 있을지 생각해 볼 수 있었습니다. 또한 Regression 문제를 Classification 문제로 전환하여 Decision Tree를 통해서도 Rule Extraction을 할 수 있다는 것을 배울 수 있었습니다.
부족하지만 읽어주셔서 감사합니다:) 피드백은 언제나 환영입니다:)
