우리나라 5054개 읍면동(2022년 3월 기준)
i7-2700에서 약 22시간
도시 좌표 구하기 참고한 블로그
위도 경도로 얻게 되는데
좌표값 차이가 너무 적게 나서 스케일링이 필요하다
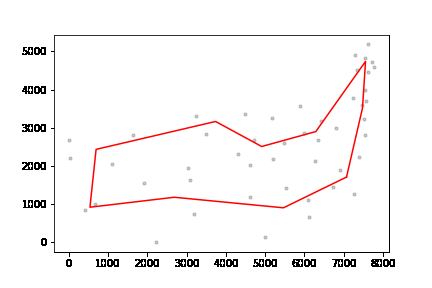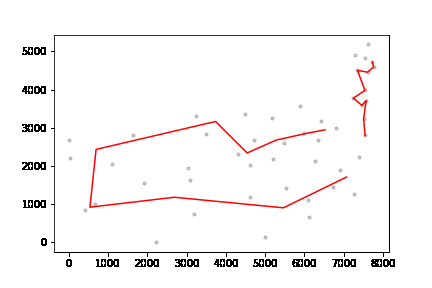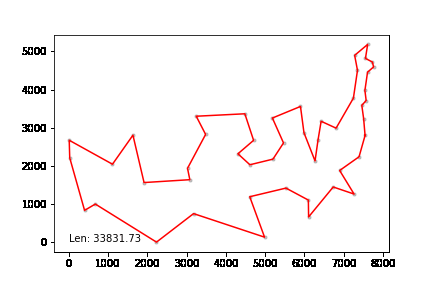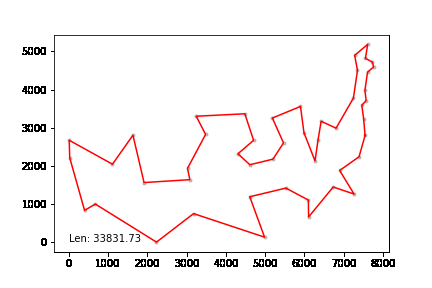
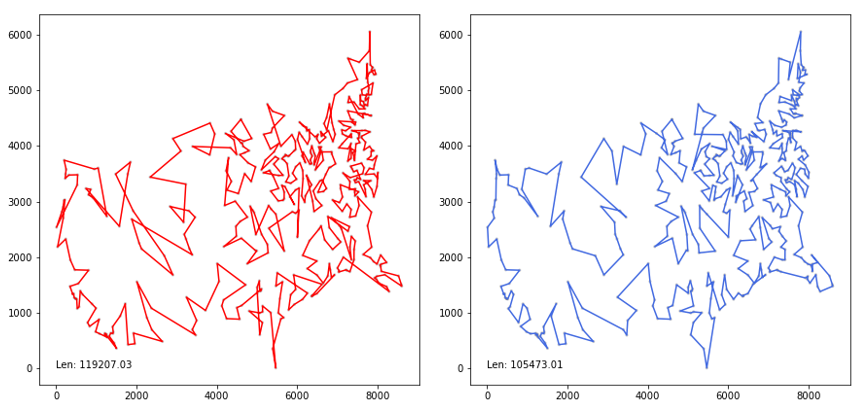
att48 데이터셋, 미국 48개 주 오래된 데이터셋인데 gif 형태로 만들어 보았다.
최적경로와 1% 이내 차이를 낸다.
TSP 최적 경로를 찾는 프로젝트
전체 코드 https://github.com/p-idx/TSP-project
프로젝트 배경
TSP 경로 찾기 문제는 대표적인 NP-hard 문제다.
완전탐색은 시간복잡도 O(n!), 분기한정법 및 동적계획법은 O(2^n*n^2) 으로
다항시간 안에 최적경로를 찾는 알고리즘은 아직 없다.
도시 간 거리테이블이 주어졌을 때,
동적계획법으로 풀면 20개 도시만 해도 상용 cpu에서 3분 이상 걸린다.
30개 이상이면 연 단위로 오래걸린다.
이보다 빠르게 최적경로를 찾는 알고리즘이 아직 없기 때문에,
근사하여 경로를 구하는 방법들이 있다.
아쉽게도 최적해를 보장하지 않는다.
다항 시간안에 풀긴 해도 지도가 어떻게 생겼냐에 따라 영향을 많이 받는 것 같다.
근사알고리즘 외에도 유전알고리즘을 통해 해를 구하기도 하는데,
경로 자체를 일종의 유전자배열처럼 고려하여
부모 유전자 경로의 일정 부분을 가져와 조합하는 방식으로 최적해를 찾아나간다.
유전알고리즘 내 교차, 선택, 돌연변이 연산 등을 잘 만들고
좋은 컴퓨팅 성능이 뒷받침되면 도시가 많은 지도에서 괜찮은 해를 찾아주기도 한다.
시간을 많이 들일수록 좋은 해가 나온다.
여기까지 TSP 알고리즘들을 공부하면서
“현실적인 시간 안에 어떻게 생긴 지도든 괜찮은 해를 찾을 수 있는가?”
라고 고민했고 이 프로젝트를 진행하게 되었다.
프로젝트 목표
1. 현실적인 시간 안에
유전 알고리즘 등 근사해 찾는 알고리즘이 사용하는 시간 대비 빠르게
2. 어떻게 생긴 지도든 + 도시 수가 많아도
일본처럼 길게 늘여지면서 대마도 같이 멀리 떨어진 섬도 있는 지도
3. 보기에 나쁘지 않은 경로를 찾자
보통 경로끼리 가로지르지 않는다
최적해가 구해진 지도가 있다면 그 거리에 최대한 근접하도록
프로젝트 내용
이 프로젝트의 해법은 다섯 단계로 이루어진다.
1. Kmeans 클러스터링을 통해 지도를 작은 지도(클러스터)로 분할
클러스터링 기법은 많지만, kmeans 클러스터링이 유클리디안 거리를 이용해 중점을 구하기 때문에
군집들의 크기가 가장 균일하다.(물론 적정한 하이퍼 파라미터 K가 주어졌을 때)
또 Gaussian mixture 모델이 비슷하게 내긴 하지만 그냥 간단명료한 kmeans를 사용하였다.
나중에 해봐야겠다.
K는 얼마나 오래 돌릴거냐에 따라 정해지는데,
여기서는 사용자가 K를 직접 정하지 않고 다음단계에서 알아서 적정 값을 고르도록 한다.
대신 K의 최대값은 받는다.
2. 클러스터들 간 동적계획법 TSP를 수행
클러스터링이 진행되면 각 클러스터들의 중점을 결과값으로 얻을 수 있는데,
이들을 대상으로 동적계획법 TSP를 수행한다.
따라서 클러스터링 할 때 K 값이 20 이하여야 현실적인 시간안에 해를 낼 수 있다.
K 값은 주어진 지도의 도시 수에 따라 정해진다.
최대값은 1단계에서 받은 K 최대값이다.
그보다 작은 값은 ‘각 클러스터 내 최대 도시의 수’ 로 나눌 수 있는 K를 정한다.
예를 들면
50개 도시가 주어지고 각 클러스터 내 최대 도시 수 가 10일 경우
K는 50 / 10 = 5 가 된다.
500개 도시가 주어질 경우, 500 / 10 = 50 이므로
사용자가 입력한 K 최대값 20을 선택한다.
K = min ( city_n / max_city_bound_in_each_cluster, user imput K )
따라서 사용자는 K 최대 바운드 값과 더불어 한 클러스터 내 최대 도시 수도 파라미터로 입력해야 한다.
추후 설명하겠지만 한 클러스터 내 최대 도시 수는 12개를 넘기기 어렵다.
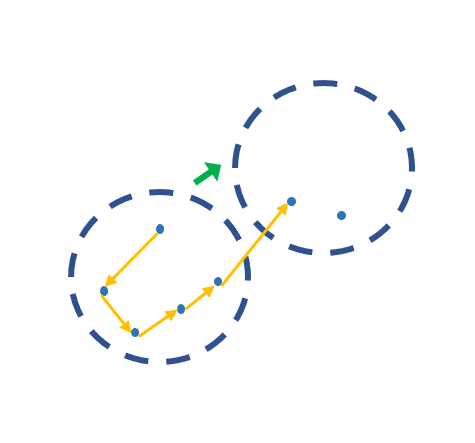
3. 클러스터들을 분열
이 부분 때문에 머리가 아팠다.
원래 이 프로젝트의 큰 틀은 지도를 소지도로 나누고,
소지도 두 개 끼리 도시간 경로(path-TSP 라 한다)를 구하고, 전부 연결하는 것이었다.
아래의 그림과 같다.
근데 클러스터링 진행시 도시가 무수히 많은 지도에서 얼마나 나눠야 할지가 문제였다.
군집간 TSP에서, 시간문제로 군집 개수를 최대 20~25개 정도로 정해버리니
도시가 수백개 수천개인 지도의 군집내 도시가 너무 많아져 버렸다.
A 군집의 도시를 하나 정하고, 다음 B 군집의 도시를 하나 정한뒤,
A 군집 내부의 도시를 전부 방문해서 B군집 도시까지 가는 경로를 구하는게 path-tsp 문제인데
(한 지도에서 시작점과 도착점을 정하고 모두 한번만 방문하는 경로)
이 문제는 그냥 TSP 문제보다 어렵다.
시간복잡도가 O(n!) 이므로 12를 초과하면 하루종일 돌려도 안끝난다.
결론적으로 한 군집 내 최대 도시수가 약 12 이하여야 한다.
이 문제를 해결하면서 있던 시행착오들을 정리했다.
초기에는 군집들을 12개 이하 도시를 가지도록 그냥 여러 개로 나누었다.
군집의 개수가 많아져도 이들을 동적계획법 TSP가 아니라 유전알고리즘 TSP로 해결하고자 하였다.
결국 군집들의 개수는 (도시수 / 12) 였기 때문에
천개 만개 도시의 지도는 너무 오래걸렸고
유전알고리즘 TSP 자체도 시간 대비 좋은 성능을 내지 못했다.
유전알고리즘은 내려놓고 다른 방안을 모색하였다.
또한 군집들의 도시수가 제각각인 것도 문제였다.
도시가 많은 군집이 가까우면서 도시가 적은 군집에게 하나씩 주는 것도 고려했다.
나중에 보니 same-size kmeans 클러스터링 이라고 명명된 기법들이 이러한 방식으로 구현되어 있었다.
하지만 이 방법은 군집의 모양새를 나쁘게 만들기도 하고
레이스 컨디션에 빠지기도 하기 때문에 역시 접었다.
(서로 인접한 군집이 최대값으로 11개, 10개 도시를 가진다면 자기들끼리 주고받는다)
물론 안그렇게 구현하면 되지만 다른 방법이 더 나을것 같았음
결과적으로 큰 군집을 분열하는 방법을 떠올렸다.
현재 적용한 방법은 군집을 인접 군집 경로를 바탕으로 반절 잘라내는 것이다.
마치 세포분열하듯이 잘라내는데 아래 그림과 같다.
잘라낸 군집들을 연결할 땐 TSP 경로를 바탕으로 가장 짧은 경로를 찾아 다시 이어준다.
가장 도시가 많은 군집을 고르고 분열하는 과정을 최대 도시수가 이하가 될 때까지 반복한다.
이 방법을 통해 위의 문제들을 부분적으로 해결할 수 있었다.
여담)
작성하면서 떠올랐는데 군집을 두개로 분열하기보다,
분할정복 아이디어로 군집 안에서 다시 클러스터링을 진행하는 것도 나쁘지 않아보인다.
군집안에 군집안에 군집안에 … 부분적으로 구현해놓았다.
일단 주석으로 추가만 해놓았고 나중에 다시 시간이 나면 코드 접합해서 이걸로 해봐야겠다.
프로젝트를 할 땐 중간중간 글로 과정을 정리하는게 필요한거 같다.
정리하면서 했으면 좋은 아이디어들을 빨리 골라낼 수 있었을 듯
4. 정리된 클러스터들과 TSP 경로를 바탕으로 path-TSP 수행
한 군집의 시작점을 선택, 다음 군집의 도착점을 선택 후
군집의 모든도시를 돌고 도착점으로 가는 경로를 만들어서 이것들을 싹 붙이면 된다.
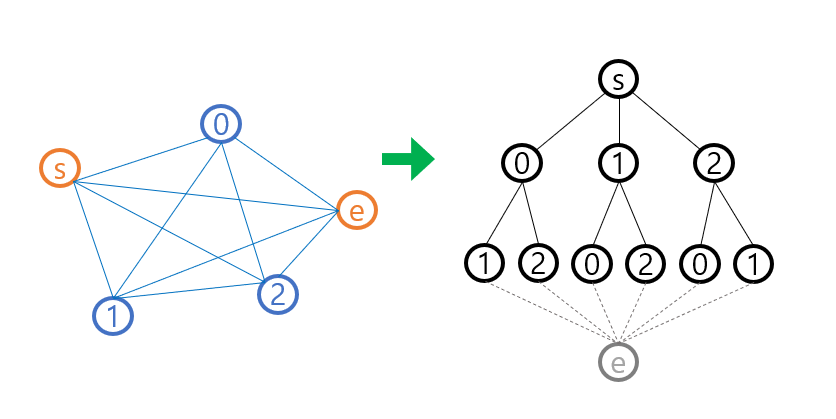
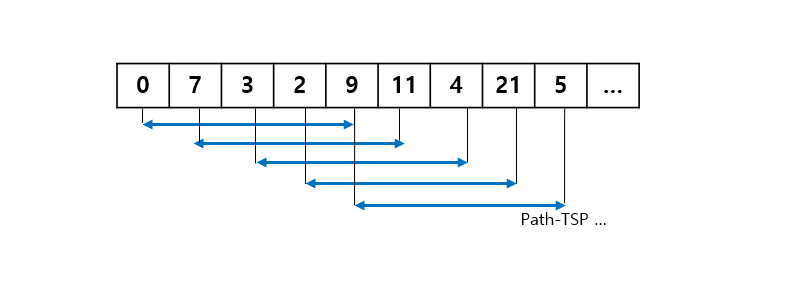
참고로 path-tsp 알고리즘은 dfs 를 통해 모든 경로를 체크하는 것으로 했으며
상태공간트리가 아래 그림처럼 그려진다.
여기에 백트래킹 아이디어로 유망한지 판단하는 과정을 넣어 시간을 줄였다.
위의 트리를 전부 순회하는것이 아니라
한번 끝까지 내려가 경로를 정했을 때, 그 거리 값을 전역에 저장해놓고
다른 경로를 탐색할 때 끝까지 내려가지 않았는데도 현재 거리가 전역 값보다 길면
그 밑의 노드 경로는 확인할 필요가 없다.
최선은 n, 최악은 n! 이다.
근데 최선과 최악의 확률은 정말 낮다.
평균적으로 시간을 반절 아낄 수 있었다.
완전탐색으로 10 ~ 11개 도시까지 현실적으로 가능했다면
백트래킹 부분을 추가해 12개까지 가능하도록 한 정도다.
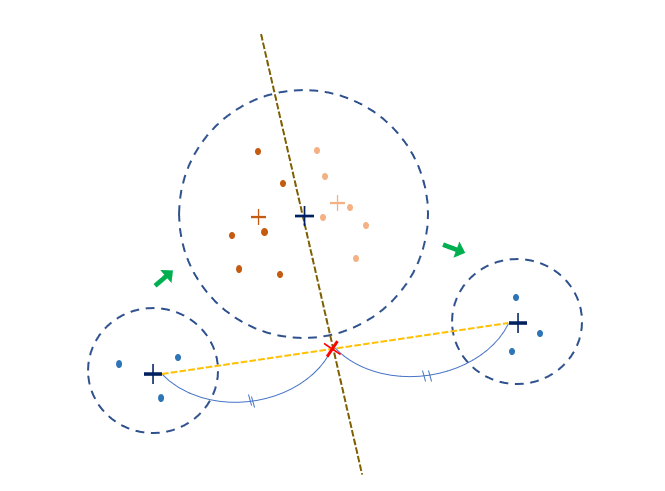
다음 군집의 도착점을 어떤 로직으로 고를 수 있을까?
처음에는 다음 군집의 도시들 중에 이전 군집의 센트로이드와 가장 가까운 도시를 고르는 것이었다.
이는 얼핏 쉬워보이지만 다음 그림처럼 어이없는 문제가 발생한다.
군집의 모양새에 따라 매우 불편하게 도착점을 골라버린다.
이전 군집의 중점과 가까운 것을 고르면
길쭉한 군집에서 그림과 같은 선택을 하기 때문에
path-TSP를 수행할 때 비효율적인 경로를 만든다.
따라서 도착점을 정하는 아이디어를 다른 방법으로 생각했는데,
우선 특징들을 골라내면서 시작한다.
얻을 수 있는 정보는 다음 군집의 모양새, 다음 경로의 방향,
이전 군집이 타고 있는 경로의 방향 등이 있다.
이들을 잘 조합하면 괜찮은 도착점을 잘 고르지 않을까 고민했고
머리가 터지기 직전에 다음과 같은 아이디어로 정리하였다.
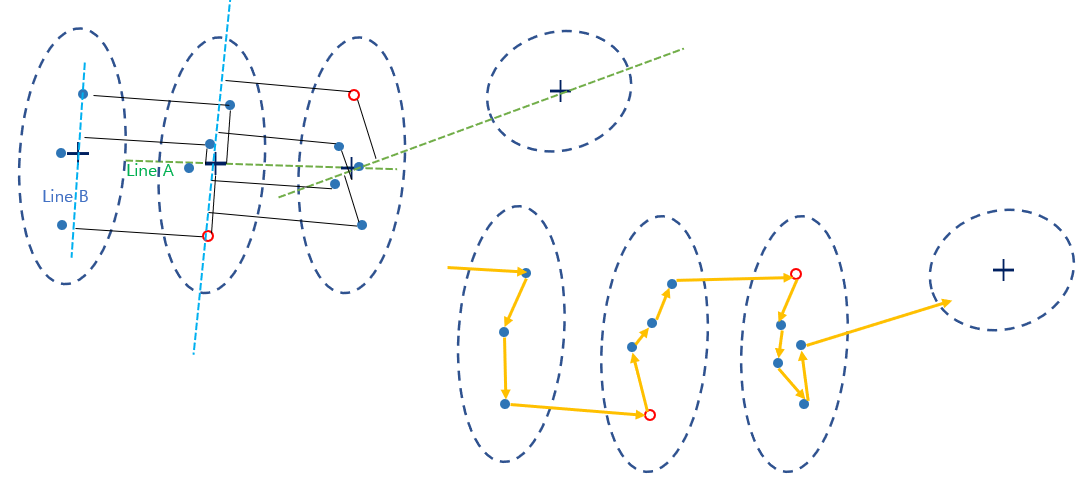
- 다음 군집과 그다음 군집의 중점을 연결하는 직선A를 긋는다.
- 시작 군집의 시작점과 그 군집의 중점을 연결하는 직선B를 긋는다.
- 다음 군집에서 직선A와는 최대한 멀고, 직선B와는 최대한 가까운 점을 순위매겨 정한다.
- 후보가 여러 개라면 시작 군집과 가장 가까운 도시로 정한다.
위 방법은 아래의 그림과 같다.
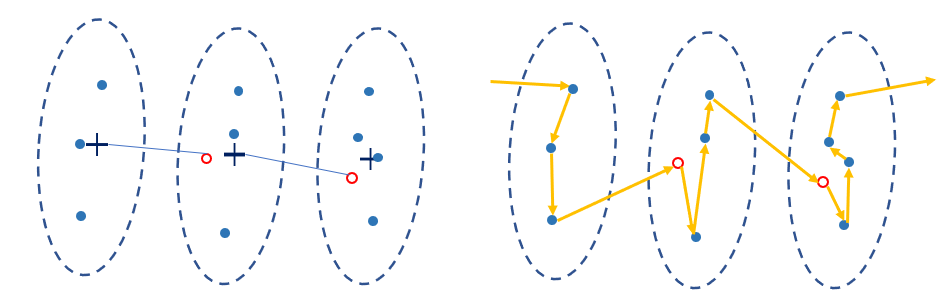
경우에 따라 비효율적으로 고르기도 하지만
군집 중점에 가까운 도착점 vs 위의 방법의 도착점 비교는 아래와 같다.
타원의 방정식과 상관계수를 활용하거나, 혹은 군집 내 도시들의 주성분 분석 등을 한다던가 하면
더 깔끔하게 군집의 모양새를 수치화할 수 있을 것 같다.
근데 그 정도로 수학이 아직 익숙치 않기 때문에...
5. 윈도우를 설정해 path-tsp를 수행
이 단계는 나중에 추가했는데, 4번의 방법도 꼬이는 경로가 나오는 한계가 있었다.
이걸 어떻게 풀지 생각했는데 근사알고리즘 중에서 꼬인 경로들을 풀어내는 걸 봤던 것 같다.
다른 일이 많아 다음에 보완하기로 하고 대신 단순한 방법으로 접근했다.
12개 이하의 구간을 한칸씩 이동하며 일일이 path-tsp를 수행하면서 풀어주면 된다.
이 단계에서는 클러스터링 정보는 더 이상 필요가 없다.
결론
이 프로젝트의 주된 로직은 군집화와 path-TSP에 있다.
path-TSP 는 팩토리얼 경우의 수를 다 뒤져서 완전한 최적해를 찾는다.
핵심은 15! 보다 10! * 100,000번이 더 적다는 것이다.
시간을 더 투자하면 더 괜찮은 경로를 내지만
클러스터링이 초기에 얼마나 잘 군집화를 해주는지,
클러스터 분열이 효과적인지,
도착점 찾기가 효과적인지 등에 따라 달라진다.
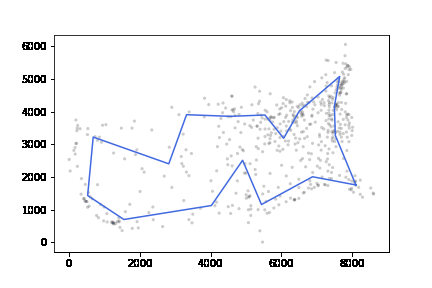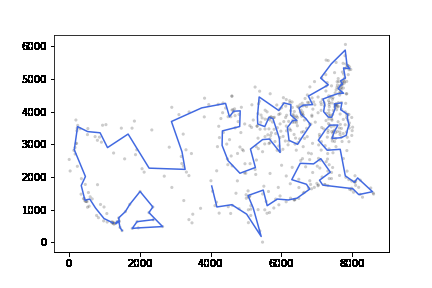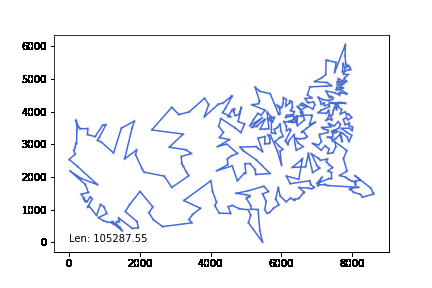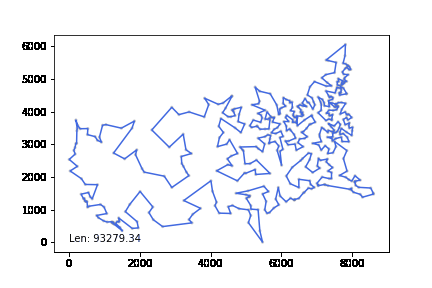
att532 set으로 테스트하였고 20분 이내 최적해보다 10% 이내의 차이를 내었다.