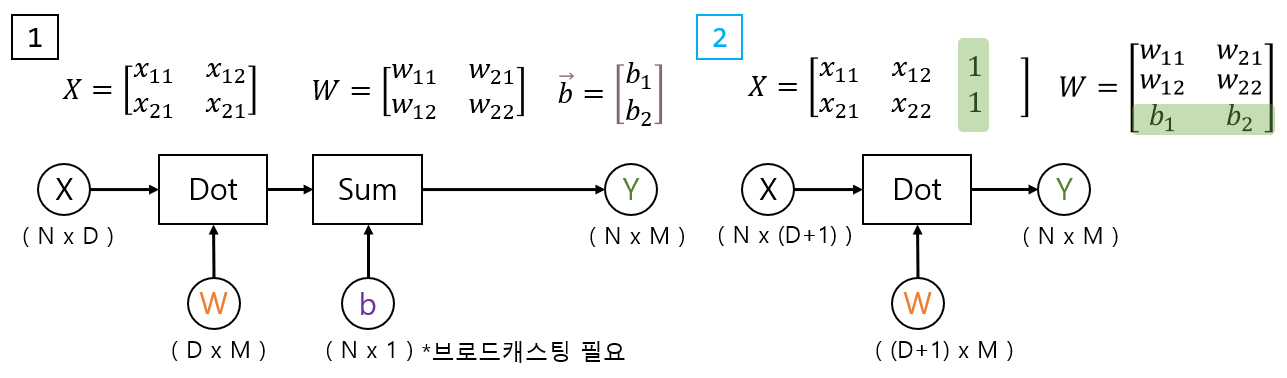
이전 포스트에서 수식을 유도하여 원소별 편미분의 값이 벡터나 행렬일 경우, 그 원소들의 합으로 표현될 수 있음을 확인했다. 이번 포스트에선 계산그래프를 스칼라 단위로 구현하고 dot, mse 연산까지 계산그래프로 구현할 것이다.
1. 계산그래프
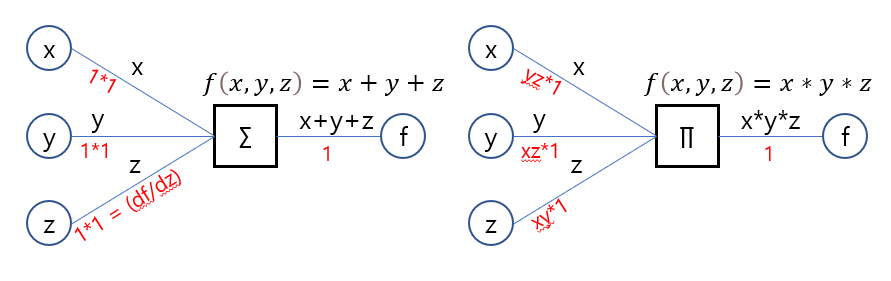
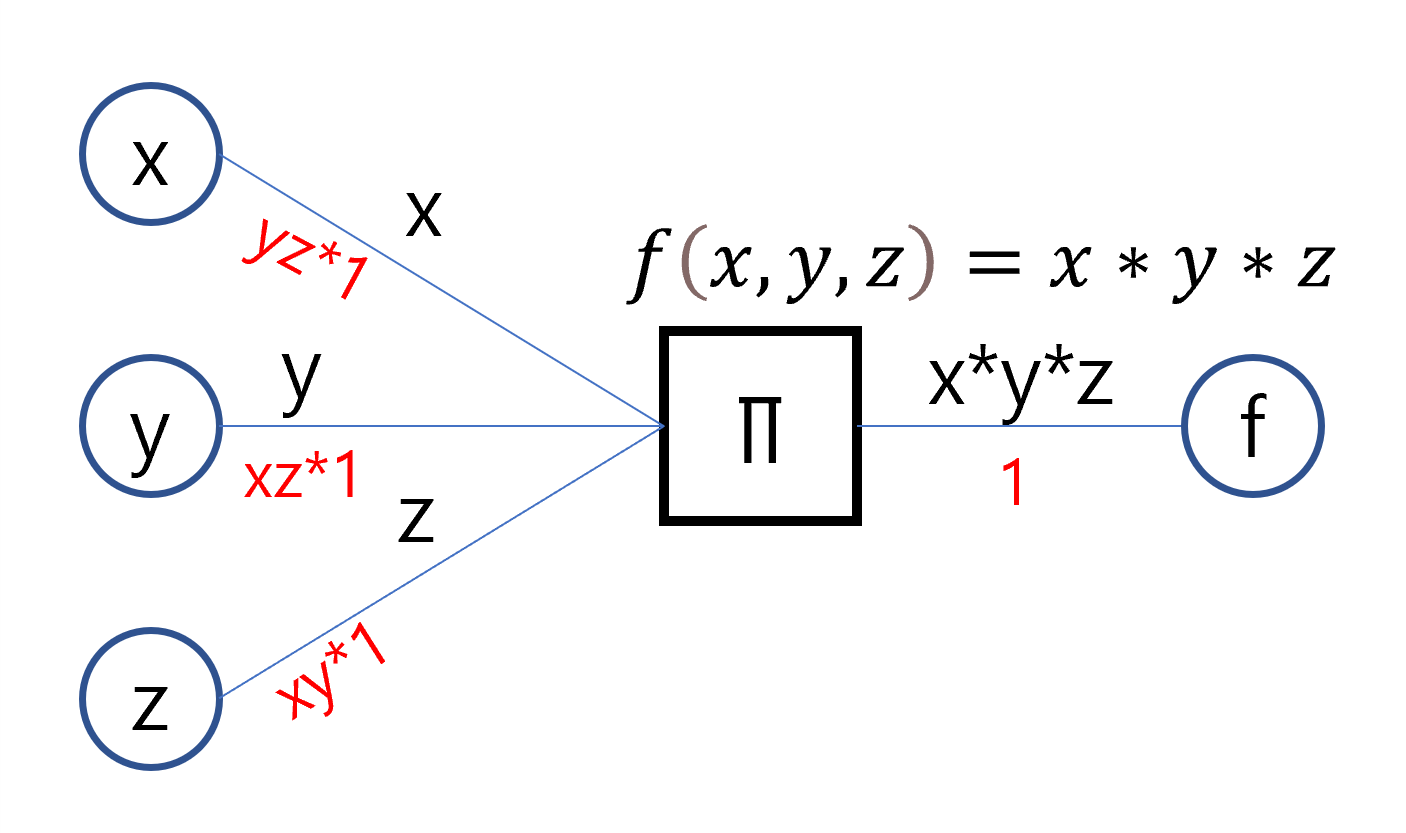
계산그래프는 함수에 입력값이 들어올 때 출력을 연결리스트처럼 표현하는 기법으로, 역으로 거슬러 올라가면 그 함수의 이전에 들어왔던 입력값과 출력값에 따른 미분값을 자동으로 계산한다. 이러한 특징이 곧 오차역전파를 구현하는 핵심이 된다. 아래 그림은 다변수의 합(summation)으로 이루어진 다항식 함수, 곱(product)으로 이루어진 다항식 함수를 계산그래프로 표현한 것이다.
원 모양의 노드는 스칼라 값, 네모 모양의 노드는 연산(or 함수)이다. 간선의 윗부분은 forward 부분으로, 왼쪽에서 오른쪽으로 흐르며 원에서 나올 땐 그대로, 연산 노드를 거치면 해당 연산의 값이 흐른다.
반대로 간선의 아랫부분은 backward 부분으로, 오른쪽에서 왼쪽으로 흐르며 연산노드를 거치면 해당 연산노드의 편미분 값들이 흐른다. 주목할 것은 미분값이 흐를 때 이전 미분값을 곱하면서 흐르는데, 이는 미분의 연쇄법칙(합성함수) 때문이다. 다양한 연산들을 엮어낼 경우 가장 오른쪽 연산부터 각각 편미분 값이 흐르며 연쇄법칙을 통해 각 연산의 미분 값이 곱해지면서 지나게 된다.
1부터 흐르게 한 이유는 연산노드의 값을 그 함수에 그대로 미분했다고 가정했기 때문이다.(해당 연산노드가 계산그래프의 최종이면 1을 넣으면서 시작한다.) df(x)/df(x) = 1 이라고 생각하면 된다.
1-1. Summation, Product Node
행렬의 곱은 원소의 곱하기와 더하기 연산만 필요함으로 위 두 연산노드만 있으면 된다.
예시코드는 아래와 같다.
import numpy as np
class ProductNode:
def __init__(self):
self.elems = None
self.grads = None
# 따로 리스트로 받지 않고 매개변수 나열로 받을 수 있도록 패킹
def forward(self, *elems):
self.elems = elems
return np.prod(self.elems)
def backward(self, dout):
self.grads = \
[dout * np.prod(self.elems[:i] + self.elems[i + 1:]) \
for i in range(len(self.elems))]
return self.grads
class SumationNode:
def __init__(self):
self.elems = None
self.grads = None
def forward(self, *elems):
self.elems = elems
return np.sum(self.elems)
def backward(self, dout):
self.grads = [dout * 1 for i in range(len(self.elems))]
return self.grads처음 구현할 땐 두 변수만 받는 더하기, 곱하기로 구현했지만 summation, product 로 구현하면 더 많은 변수를 한번에 처리할 수 있어 이렇게 구현하였다. summation 노드는 사실 더하기로 이루어진 다항식이기 때문에 편미분 시 모두 1이다. backward 멤버함수는 dout을 받는데, dout을 곱해주어 이전에 흘러오는 미분값을 곱해 연쇄법칙을 구성한다.
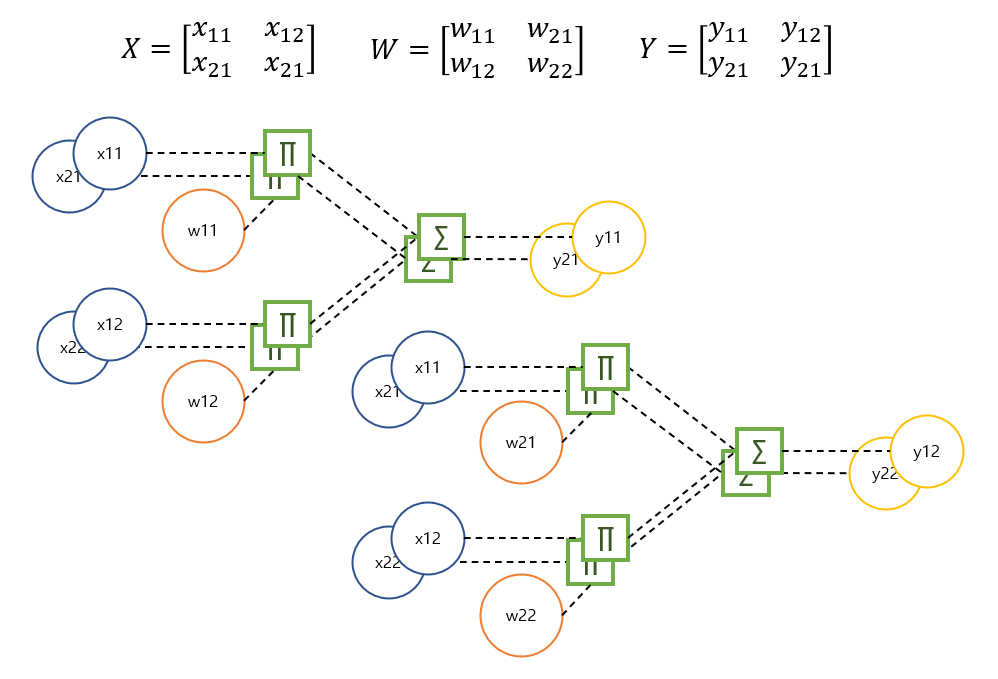
1-2. Dot layer
이제 위의 스칼라 계산그래프를 이용해 행렬곱 연산을 만들어보자. 행렬곱 연산은 말그대로 행렬을 다루기 때문에 행렬 곱의 규칙에 따라 출력을 구상해야 한다. 스칼라 연산 노드들을 뭉쳐 만들었으므로 레이어라 칭하자.
2 by 2 행렬끼리의 곱은 위와같은 계산그래프 형태를 갖는다. 복잡해 보이지만 중복되는 부분이 많을 뿐이다. 행렬곱 규칙에 따라 product 노드는 8개, summation 노드는 4개가 필요하다. 입력은 행렬 X를 받고(행렬 W는 멤버변수로 존재) 행렬 Y를 출력하는 forward 함수를 구상하여 행렬 곱을 계산한다. 얼핏 보면 트리 따위의 자료구조를 만들어야 할까 싶지만, 2차원 리스트의 인덱스 접근을 통해 다중 for문으로 해결할 수 있다. 각 연산 노드들을 가지는 2차원 리스트를 만들어 계산할 원소의 위치마다 적용하도록 하면 된다.
class DotLayer:
def __init__(self, n, W):
self.X = None
self.W = W
self.n = n
self.Ms = [[[ProductNode() for _ in range(W.shape[0])] \
for _ in range(W.shape[1])] for _ in range(n)]
self.Ss = [[SumationNode() for _ in range(W.shape[1])] \
for _ in range(n)]
self.dW = None
def forward(self, X):
# 행렬곱에 의해 출력될 틀
ret = np.zeros((self.n, self.W.shape[1]), dtype=np.float32)
for i in range(self.n):
for j in range(self.W.shape[1]):
outs = []
for k in range(self.W.shape[0]):
outs.append(self.Ms[i][j][k].forward(X[i][k], \
self.W[k][j]))
ret[i][j] = self.Ss[i][j].forward(*outs)
return ret
def backward(self, dout):
# 각 원소별 미분값이 출력될 틀
dX = np.zeros((self.n, self.W.shape[0]), dtype=np.float32)
self.dW = np.zeros_like(self.W)
for i in range(self.n):
for j in range(self.W.shape[1]):
dout_2s = self.Ss[i][j].backward(dout[i][j])
for k, dout_2 in enumerate(dout_2s):
dx, dw = self.Ms[i][j][k].backward(dout_2)
dX[i][k] += dx
self.dW[k][j] += dw
return dXbackward 함수의 경우 각 스칼라 노드로 향해가는 과정에서 결과 행렬을 행렬 X로 혹은 행렬 W로 미분하게 된다. 이전 포스트에서 보았다시피 각각 영향을 미치는 원소들의 편미분 합으로 나타낼 수 있으므로 처음에 미분값 행렬을 0을 채운 행렬로 만든 다음, 각각의 위치와 같은 원소에 backward 로 도달할 때 마다 나온 값을 0을 채운 행렬에 차례로 누적하면 된다. 이전 포스트에선 dW 만 구했지만, dX 까지 구하는 이유는 딥러닝 은닉층에서 활용할 수 있기 때문이다.
Dot 레이어를 만들었으니 결과를 테스트해보자.
X = np.array([[1,2], [3,4]])
W = np.array([[5,6], [7,8]])
al = DotLayer(2, W)
Y = al.forward(X)
dX = al.backward(np.array([[1,1],[1,1]]))
print(f'Y:\n {Y}')
print(f'X.T:\n {X.T}')
print(f'W.T:\n {W.T}')
print(f'dX:\n {dX}')
print(f'dW:\n {al.dW}')dout으로 들어오는 행렬을 1로 구성된 행렬(Y와 사이즈가 같아야 한다.)을 넣으면 dX는 dout * W.T 와 같고, dW는 X.T * dout 임을 알 수 있다. 행렬이므로 교환법칙이 성립하지 않는다는 것을 상기하자.
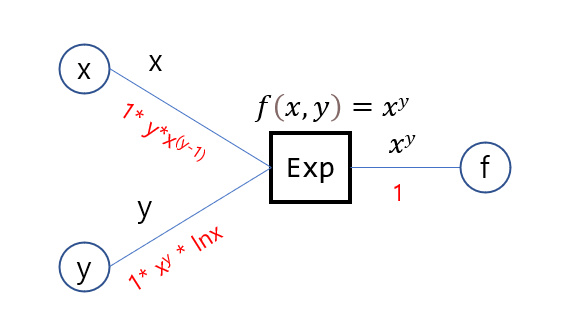
1-3. Exponent node
MSE 함수를 구성하기 전에 연산노드가 하나 더 필요하다. 지수함수를 나타내는 exponent node이다. 아래 그림처럼 구성되며, 미분 대상이 밑이든 지수이든 두 경우 모두의 미분값을 계산한다.
class ExponentNode:
def __init__(self):
self.base = None
self.exponent = None
self.dbase = None
self.dexponent = None
def forward(self, base, exponent):
self.base = base
self.exponent = exponent
return base ** exponent
def backward(self, dout):
self.dbase = dout * (self.exponent * (self.base) ** (self.exponent - 1))
# 지수로 미분 시 밑 0이거나 너무 작으면 안됨
if self.base < 0.0:
self.base = -self.base
log_base = -self.base + 1e-7 if self.base <= 0 else self.base
self.dexponent = dout * (self.base ** self.exponent) * np.log(log_base)
return [self.dbase, self.dexponent]지수연산 노드가 필요한 이유는 mean Squared error 때문이다. 사실 Product Node를 적절히 활용하면 되지만 향후 시그모이드, 소프트맥스, 크로스 엔트로피 손실함수 등에서 활용할 수 있도록 만들어 두었다. 덧붙여 지수연산 노드는 밑과 지수 두 가지 변수만 받는다.
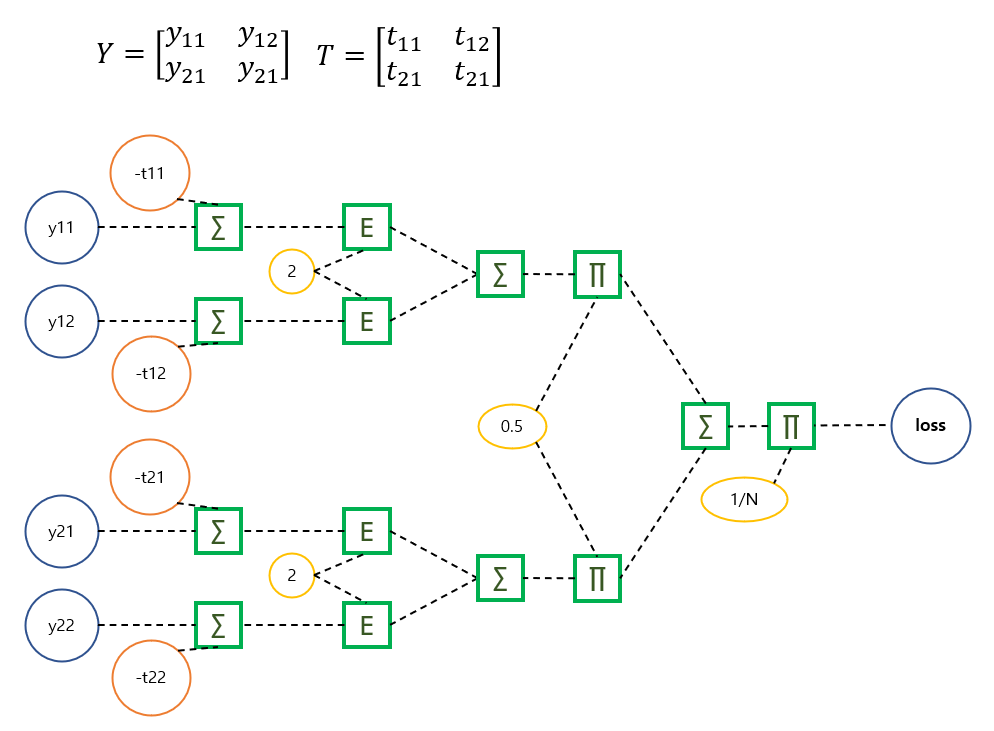
1-4. MSE layer
대망의 평균제곱오차 손실함수의 레이어를 구상하겠다.
복잡해 보이지만 중복된 곳이 많고 행렬 Y의 원소별 위치에 따라 2차원 리스트로 연산 노드들을 접근하면 된다. 정답행렬 T는 음수로 만들어 Y에 더하고, 각 원소들을 제곱하고 행 단위로 더한뒤, 다시 1/2를 곱하고 모든 열을 다 더하고(...) 데이터 개수만큼 나누어 주면 loss 값이 나온다.
class MSELayer:
def __init__(self, T):
self.T = T
self.Ss_1 = [[SumationNode() for _ in range(T.shape[1])] for _ in range(T.shape[0])]
self.Es = [[ExponentNode() for _ in range(T.shape[1])] for _ in range(T.shape[0])]
self.Ss_2 = [SumationNode()for _ in range(T.shape[0])]
self.Ms = [ProductNode()for _ in range(T.shape[0])]
self.lastSum = SumationNode()
self.lastMul = ProductNode()
def forward(self, Y):
last_outs = []
for i in range(Y.shape[0]):
outs = []
for j in range(Y.shape[1]):
out = self.Ss_1[i][j].forward(Y[i][j], -self.T[i][j])
outs.append(self.Es[i][j].forward(out, 2))
out = self.Ss_2[i].forward(*outs)
last_outs.append(self.Ms[i].forward(out, 0.5))
out = self.lastSum.forward(*last_outs)
return self.lastMul.forward(out, 1.0 / len(last_outs))
def backward(self, dout):
dY = np.zeros_like(self.T, dtype=np.float32)
dout = self.lastMul.backward(dout)[0]
dout_2s = self.lastSum.backward(dout)
for i, dout_2 in enumerate(dout_2s):
dout_2 = self.Ms[i].backward(dout_2)[0]
dout_3s = self.Ss_2[i].backward(dout_2)
for j, dout_3 in enumerate(dout_3s):
dout_3 = self.Es[i][j].backward(dout_3)[0]
dY[i][j] = self.Ss_1[i][j].backward(dout_3)[0]
return dYMSE 레이어는 생성할 때 정답행렬을 넣어주고, forward 할 때 Y 행렬을 넣어주면 loss 값을 계산할 수 있다. backward는 이 레이어가 최종단에 있기 때문에 단순히 1을 넣어주면 된다.
Dot 레이어와 MSE 레이어를 완성했으니 다중회귀분석 모델을 만들어 테스트하겠다.
2. 오차역전파(스칼라 단위) 경사하강법을 통한 다중회귀분석
유틸리티가 sklearn의 LinearRegression 과 동일하도록 구성했다.
class LinearRegression:
def __init__(self):
self.W = None
self.Y = None
def get_W(self):
return self.W
weights = property(get_W)
def fit(self, X, t, lrate = 0.001, bias=True, iter=1000, printIter=False):
# preprocessing
X = np.array(X, dtype=np.float32)
if X.ndim != 2:
raise Exception("X shape is not (N, 1) matrix")
t = np.array(t, dtype=np.float32).reshape((len(t),-1))
if len(X) != len(t):
raise Exception("len(X) != len(t)")
self.W = np.zeros((X.shape[1], 1))
if bias:
X = np.concatenate((X, np.ones((X.shape[0], 1))), axis=1)
self.W = np.concatenate((self.W, np.zeros((1,1))), axis=0)
# preparing layers for backprop and grad descent
af = AffineLayer(X.shape[0], self.W)
ms = MSELayer(t)
out = af.forward(X)
ms.forward(out)
for i in range(iter):
dout = ms.backward(1)
af.backward(dout)
af.W -= lrate * af.dW
out = af.forward(X)
loss = ms.forward(out)
if printIter:
if i % (iter//10) == 0 and i != 0:
print(f'iter: {i} loss: {loss}')
print(af.W.squeeze())처음에 LinearRegression 객체를 생성하고, fit 함수를 통해 계수를 찾는다. bias의 경우 하단과 같이 두가지 구성을 통해 만들 수 있는데, 행렬에 concat하는 방법이 훨씬 간단함으로 후자의 방법을 사용한다.
sklearn dataset에 있는 붓꽃 패키지를 회귀분석 해보았다. 결과값은 다음과 같으며, 이는 sklearn의 선형회귀 방법과 상당히 비슷한 결과를 내었다. 하지만 시간은 20분이 넘게 걸려서 사실상 수치미분을 통한 경사하강법 보다 느렸다.
만든 모델 ->
W = [-0.10406646 -0.03316504 0.2296437 0.60228353], b = 0.12368906
sklearn ->
W = [-0.11190585 -0.04007949 0.2286450 0.60925205], b = 0.186495247206253
3. 결론
이번 포스팅에서는 행렬 곱의 미분값이 각 행렬의 전치행렬이면서 곱셈의 위치도 각각 바뀌는 것을 스칼라 단위로 구현하여 실제 그렇게 되는지 확인했던 것에 의의가 있다.
오차역전파가 딥러닝을 구현하는데 사용되는 이유는 실제 수치미분보다 빠르게, 자동으로 미분하는 것에 그 핵심이 있다. 행렬곱은 단순히 전치행렬 곱으로 나타날 수 있다는 것(추가로 MSE 역시 훨씬 간략하게 행렬 곱셈으로 나타낼 수 있다) 는 것을 여기서는 밝히기만 했지 직접 사용하지는 않았다. 다음 포스팅에선 위의 스칼라 단위가 아닌 행렬 단위로 구현해 속도를 높여보겠다.