오차역전파 내부 원리 - 3 (실제 구현)

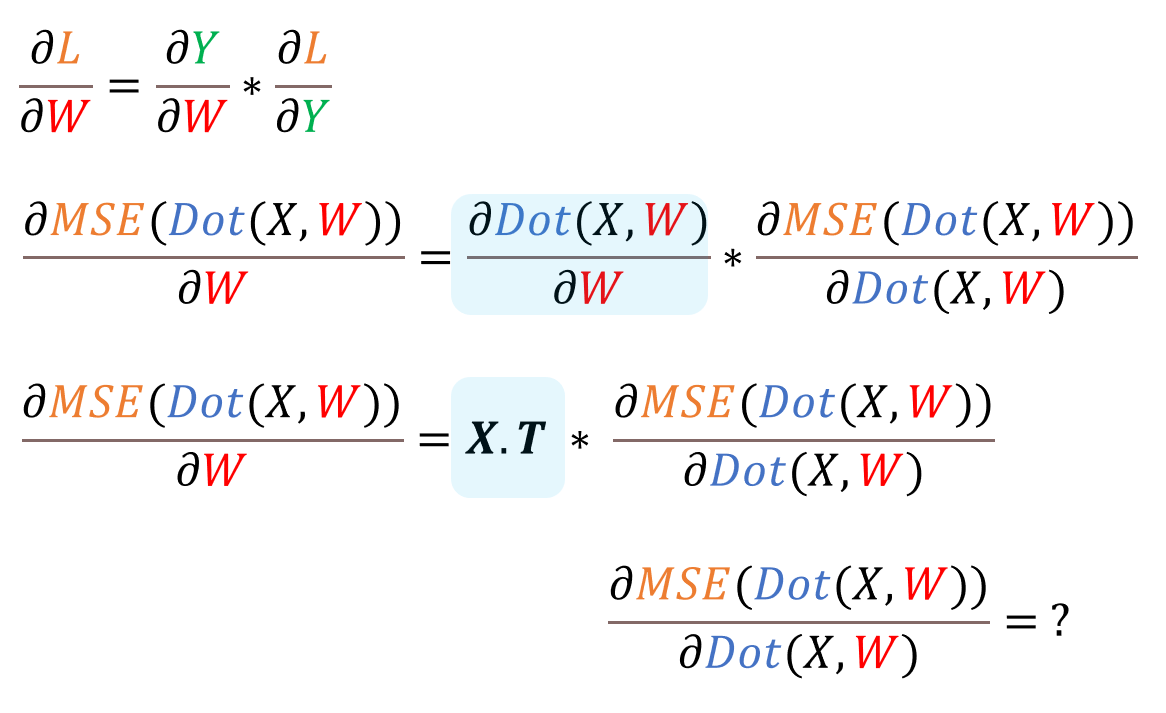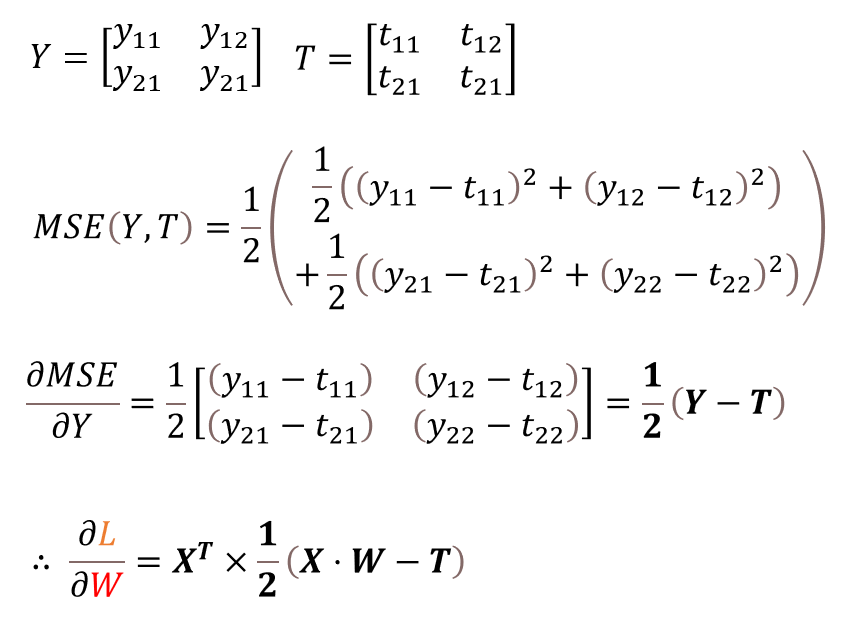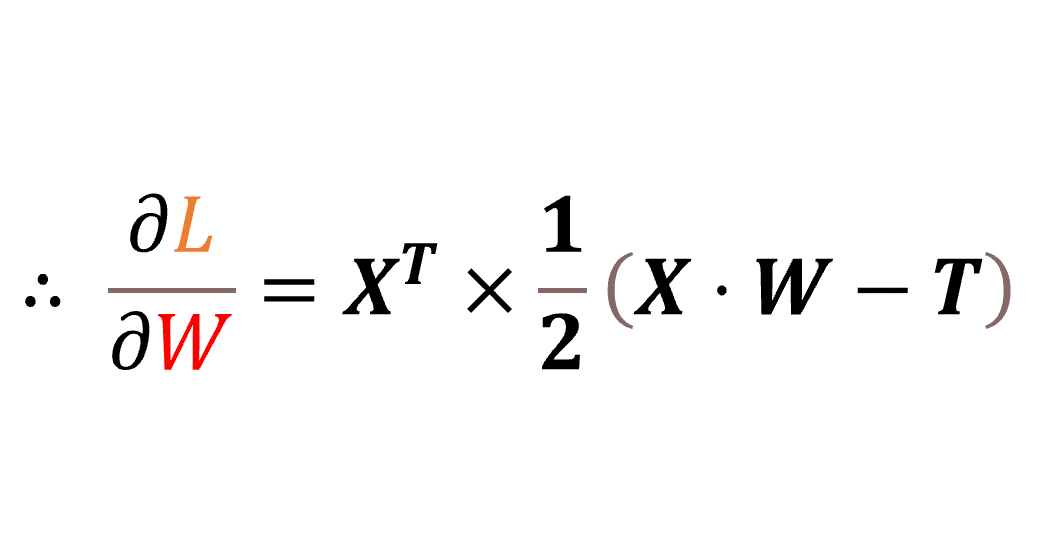
이번 포스트에선 각 레이어 과정에서 확인한 간략한 결과들을 직접 대입, 활용하여 빠른 회귀분석을 구현한다.

1. 연쇄법칙으로 분해

우리는 이전포스트에서 행렬곱의 미분이 어떤식으로 나타나는지 계속 확인하였다. 그럼 이제 MSE의 미분은 어떻게 나타나는지 알아보자.

2. MSE 미분

이럴수가 말도 안되게 간결해져 버렸다. 실제로 다중회귀분석이 이루어 지는지 코드로 확인하겠다.

3. 최종 결과

import numpy as np

from sklearn.datasets import load_iris
from sklearn.linear_model import LinearRegression as SkLinear

iris = load_iris()
X, t = iris['data'], iris['target'].reshape(-1, 1)
W = np.full((X.shape[1], 1), 0.1)

# add bias
nX = np.concatenate((X, np.ones((X.shape[0], 1))), axis=1)
nW = np.concatenate((W, np.full((1,1), 0.2)), axis=0)

def forward(X, W, t):
    # dot
    Y = np.dot(X, W)
    # mse
    return np.sum(0.5 * ((Y - t) ** 2)) * 0.5

def backward(X, W, t):
    # dmse
    dY = 0.5 * (np.dot(X, W) - t)
    # ddot
    return np.dot(X.T, dY)

iter_num = 100000

for i in range(iter_num):
    loss = forward(nX, nW, t)
    if i % (iter_num//10) == 0:
        print(f'loss: {loss:.5f}, W: {nW.squeeze()}')
    
    # W update
    nW -= 0.0001 * backward(nX, nW, t)

sk_lr = SkLinear()
sk_lr.fit(X, t)
print('sklearn result:', sk_lr.coef_, sk_lr.intercept_)

loss: 1.74015, W: [-0.11184572 -0.04004399 0.22863744 0.60922891 0.18608863]
sklearn result: [[-0.11190585 -0.04007949 0.22864503 0.60925205]][0.18649525]

이 코드에서는 dot 부분과 mse 부분을 하나의 forward, backward 함수에서 퉁쳐 이루어지도록 했다. 실행시간이 채 10초가 되지 않는데 sklearn의 회귀분석과 거의 일치하는 결과를 낸다. sklearn은 내부적으로 정규방정식을 사용하는 것으로 보여 더 정확하고 빠르게 계산하는 것 같다.

참고로 정규방정식은 데이터의 특징이 많을 수록 행렬의 크기가 커지기 때문에(유사역행렬 개념) 빅데이터를 다룰 땐 이와 같은 경사하강법을 사용해야 한다.

오차역전파는 연쇄법칙, 사람이 직관적으로 계산해 알 수 있는 도함수 (ex. y = x^2 -> 2x^1), 간결한 행렬 표현을 직접 대입해 활용할 수 있기 때문에 미세값을 직접 일일이 넣는 수치미분보다 훨씬 빠르게 가중치를 업데이트 할 수 있다.

이 시리즈를 포스팅하면서 행렬곱의 미분원리를 알게 되었고 동시에 오차역전파의 전반적인 구조가 어떻게 빠른 학습을 해내는지 알 수 있었다. 여기에선 다중회귀분석의 결과만 빠르게 확인하고자 퉁쳐서 만들었지만, 레이어 단위로 구현하면서 활성화함수, 소프트맥스 함수 등을 같이 구현하면 쉽게 딥러닝 뉴런을 구성할 수 있다.

이후부턴 많은 책과 강의, 블로그에서 역전파 구현을 다루고 있기 때문에 여기까지 마무리하겠다.