오늘 리뷰할 논문은 마이크로소프트에서 낸 DeBERTa 논문이다.
아래 포스트를 먼저 보면 도움이 될 것이다.
Summary
논문은 두 새로운 기술을 도입해 BERT와 RoBERTa를 향상시키는 DeBERTa (Decoding-enhanced BERT with disentangled attention)를 제안한다. 첫번째 기술은 disentangled attention mechanism으로 각 단어가 content와 position을 encode하는 두 vectors로 표현되며 단어들 사이 attention weights는 각각 그들의 contents와 relative position에 대한 disentangled matrices를 이용해 계산된다. 둘째로 pre-training 중에 masked tokens을 예측하기 위해 decoding layer에서 absolute position을 통합하기 위해 enhanced mask decoder가 사용된다. 추가로 모델의 일반화를 돕기 위해 fine-tuning 중에 새로운 virtual adversarial training method가 사용된다. 논문은 이 기술들이 pre-training에 효과적이고 natural language understand (NLU)와 natural langauge generation (NLG) downstream tasks 성능을 향상시킴을 보인다.
- Disentangled attention
input layer의 각 단어가 word (content) embedding과 position embedding의 합인 하나의 벡터로 표현되는 BERT와 달리 DeBERTa의 각 단어는 각각 content와 position을 encode하는 두 벡터로 표현되며 단어들 사이 attention weights는 각각 그들의 contents와 relative position에 기반한 disentangled matrices를 사용해 계산된다. 이는 단어쌍 사이 attention weight가 content뿐 아니라 relative position에도 의존한다는 관측에서 영감을 받았다(단어끼리 멀리 있을 때보다 가까울 때 더 연관성이 높으니까).
- Enhanced mask decoder
BERT처럼 DeBERTa도 MLM을 이용해 pre-train한다. DeBERTa는 MLM을 위해 context words의 content와 position information을 사용한다. disentangled attention mechanism은 context words의 content와 relative position을 이미 고려하고 있지만, 많은 경우에 absolute position이 예측에 중요하다. DeBERTa는 softmax layer 직전에 absolute word position embedding을 통합해 (softmax layer에서) aggregated contextual embeddings에 기반해 masked word를 예측(decode)한다.
sequence 내 position i의 token에 대해 content와 position j의 token과의 relative position을 나타내는 두 벡터 로 표현한다. token i와 j의 cross attention score은 다음과 같이 네 개의 항으로 계산한다.
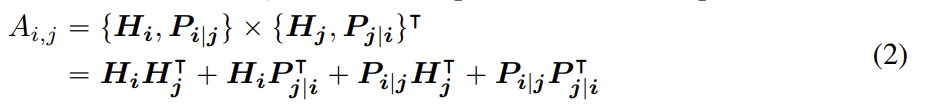
즉 단어 쌍의 attention weight는 disentangled matrices를 사용해 네 attention scores, 다시말해 content-to-content, content-to-position, position-to-content, position-to-position로 계산될 수 있다.
이미 존재하는 relative position encoding 방식은(Shaw et al., 2018; Huang et al., 2018) attention weights를 계산할 때 relative position bias를 계산하기 위해 separate embedding matrix를 사용한다. 이는 content-to-content와 content-toposition 항만 사용해 attention weight를 계산하는 것과 동일하다. 논문은 단어쌍의 attention weight이 content뿐 아니라 (content-to-position와 position-to-content 항 둘 다 사용해야 완전히 model될 수 있는) relative position에도 의존하기 때문에 position-to-content 항도 중요하다고 주장한다. relative position embedding을 사용하기 때문에 position-to-position 항은 추가적인 정보를 별로 제공하지 않는다고 생각해 구현에서는 식 (2)에서 항을 제거했다.
single-head attention를 예로 들어 (원본 Transformer의 일반적인) single-head attention는 다음과 같이 공식화된다.
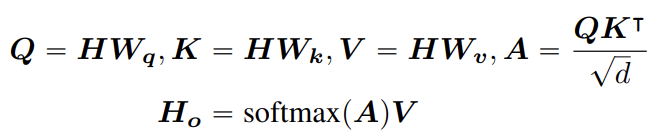
는 input hidden vectors를 의미하고 는 self-attention의 output, 는 projection matrices, 는 attention matrix, N은 input sequence의 길이, d는 hidden states의 dimension을 나타낸다.
k를 maximum relative distance라 두고 를 token i에서 j까지 relative distance로 다음과 같이 정의한다.
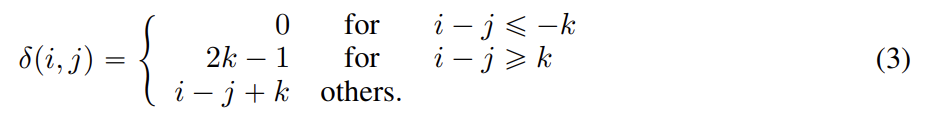
relative position bias를 가진 disentangled self-attention를 식 (4)와 같이 표현할 수 있다. 는 각각 projection matrices 로 생성된 projected content vectors고 는 모든 layers에 걸쳐 공유되는(즉 순전파 중에 값이 고정된) relative position embedding vectors이고 은 projection matrices 로 생성된 projected relative position vectors다.
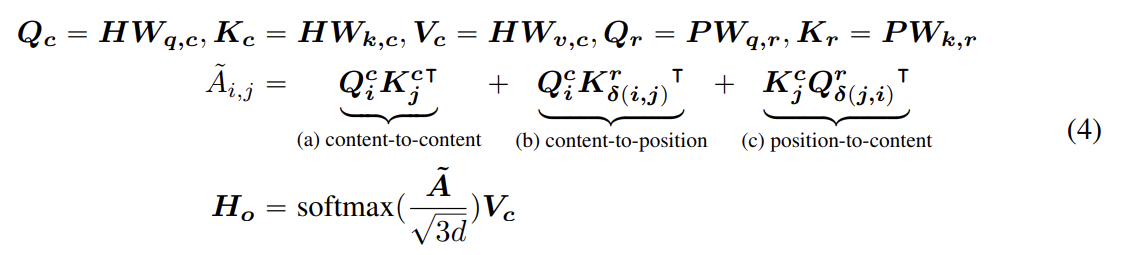
는 attention matrix 의 element고 token i에서 j로 attention score을 나타낸다. 는 각각 의 i, j, δ(i, j), δ(j, i)번째 row다. 이때 position-to-content 항에선 δ(i, j)가 아니라 δ(j, i)를 사용했는데 position-to-content가 i의 query position에 대한 j의 key content의 attention weight을 계산하기 때문이다.
마지막으로 에 scaling factor 를 적용한다. 이 factor는 특히 large-scale PLMs(pre-trained language models)에 대해 학습으르 안정화시키는 데 중요하다.

길이 N의 input sequence에 대해 각 token의 relative position embedding를 저장하려면 공간복잡도 가 필요하다. 그러나 content-to-position를 예로 들어, 와 모든 가능한 relative positions의 embeddings이 항상 의 subset이기 때문에 모든 queries에 대해 attention 계산에서 을 재사용할 수 있다.
실험에선 pre-training 시 maximum relative distance k를 512로 두었다. disentangled attention weights는 Algorithm 1을 이용해 효율적으로 계산될 수 있다. δ를 식 (3)에 따라 relative position matrix라 둔다. 각 query에 다른 relative position embedding matrix를 할당하는 대신 각 query vector 에 를 곱하고 relative position matrix δ를 index로 삼아 attention weight을 추출한다. position-to-content attention score를 계산하기 위해 각 key vector 에 을 곱해 attention matrix 의 column vector인 를 계산한다. 마지막으로 relative position matrix δ를 index로 삼아 상응하는 attention score을 추출한다. 이 방법은 각 query에 대한 relative position embedding을 저장하는 메모리를 할당할 필요가 없고 (을 저장하기 위한) 공간복잡도를 로 감소시킬 수 있다.
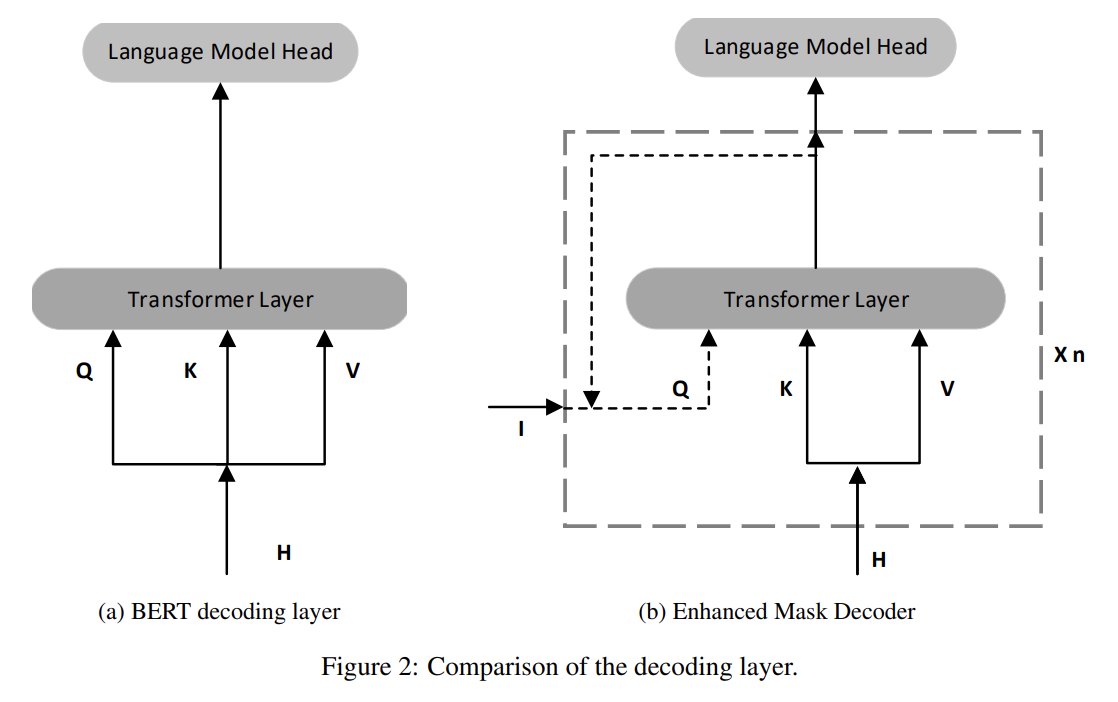
앞서 설명했듯 DeBERTa는 relative position를 보완하도록 absolute position도 고려한다. absolute position을 통합하는 방법은 두 가지가 있다. BERT는 input layer에 absolute position을 포함한다. DeBERTa는 모든 Transformer layer 직후, 그러나 masked token prediction을 위한 softmax layer 이전에 absolute position을 포함한다. 이 방법으로 DeBERTa는 모든 Transformer layers 내의 relative position을 포착하고 absolute position은 masked word를 decode할 때 보완적인 정보로만 사용한다. 따라서 DeBERTa의 decoding component를 Enhanced Mask Decoder (EMD)라고 이름붙였다.
또 fine-tuning에서 Miyato et al. (2018); Jiang et al. (2020)가 소개한 알고리즘의 변형인 새로운 virtual adversarial training algorithm인 Scale-invariant-Fine-Tuning (SiFT)를 도입한다. Virtual adversarial training는 모델의 일반화를 향상시키는 regularization 방법이다. 이는 input에 작은 순열을 만드는 식으로 만들어지는 adversarial examples를 향한 model의 robustness를 향상시킨다. task-specific example이 주어졌을 때 그 example의 adversarial perturbation과도 동일한 output distribution을 생성하도록 모델이 regularize된다.
NLP task에서 순열은 original word sequence가 아니라 word embedding에 적용된다. 그러나 embedding vectors의 value ranges (norms)는 서로 다른 words와 models 간에 굉장히 다르다. 분산은 큰 모델일수록 커지고 adversarial training에 불안정성을 초래한다.
layer normalization에 영감을 받아 논문은 순열을 normalized word embeddings에 적용하는 식으로 학습 안정성을 높이는 SiFT algorithm을 제안한다. 구체적으로 DeBERTa를 downstream task에 fine-tuning할 때 SiFT는 우선 word embedding vectors를 stochastic vectors로 normalize한 후 normalized embedding vectors에 순열을 적용한다. normalization은 fine-tuned models의 성능을 상당히 향상시켰고 큰 DeBERTa 모델일수록 향상이 두드러졌다.
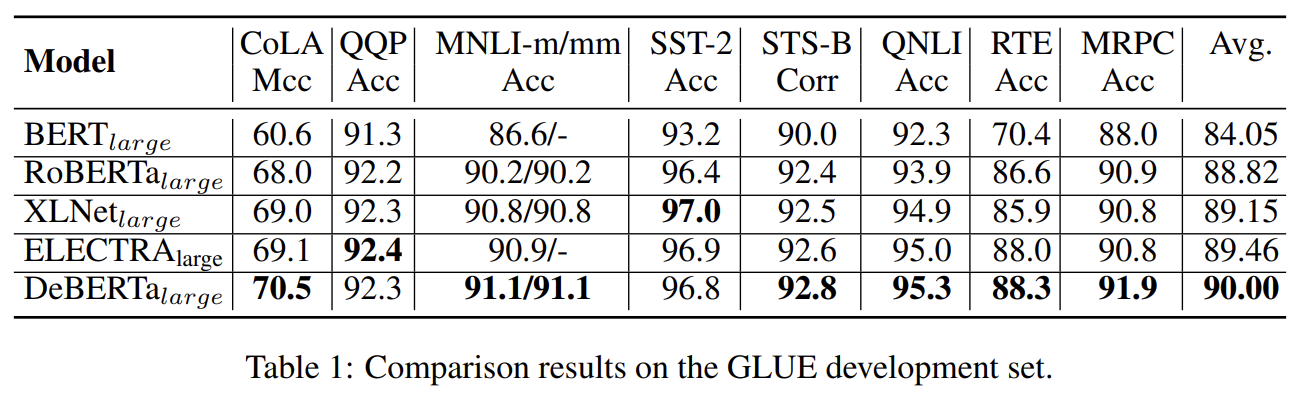
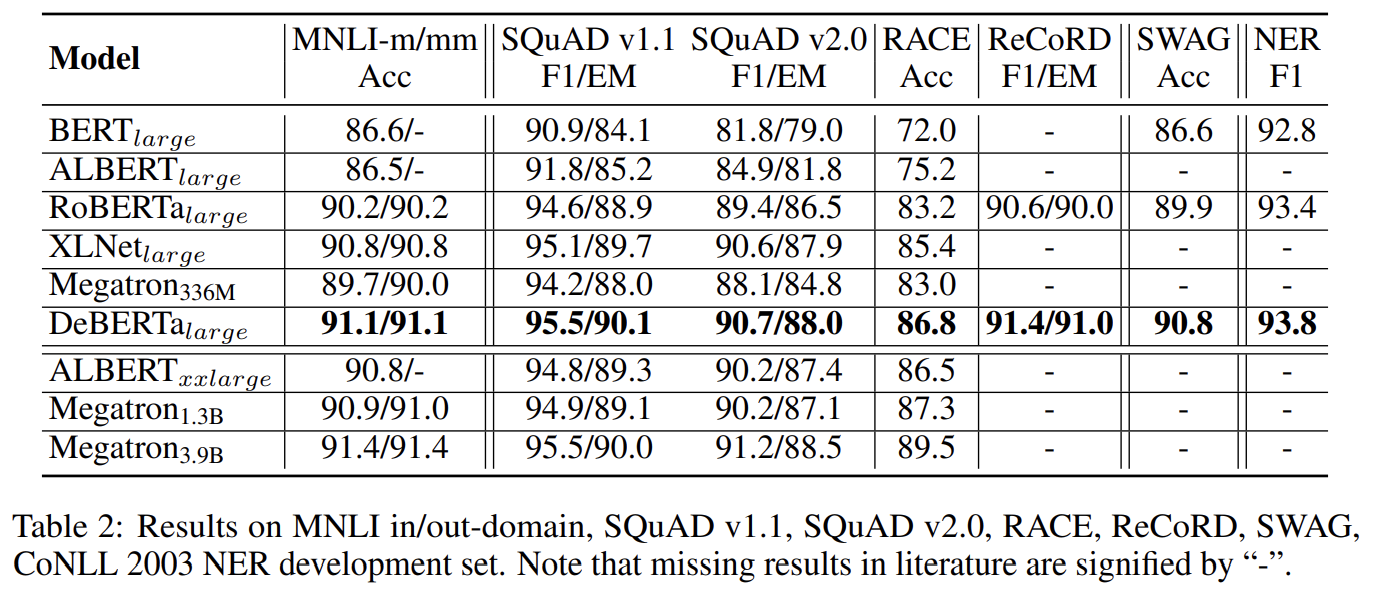
Large 모델의 성능 실험 결과다. 설명은 생략한다.

Base 모델의 실험 결과다.
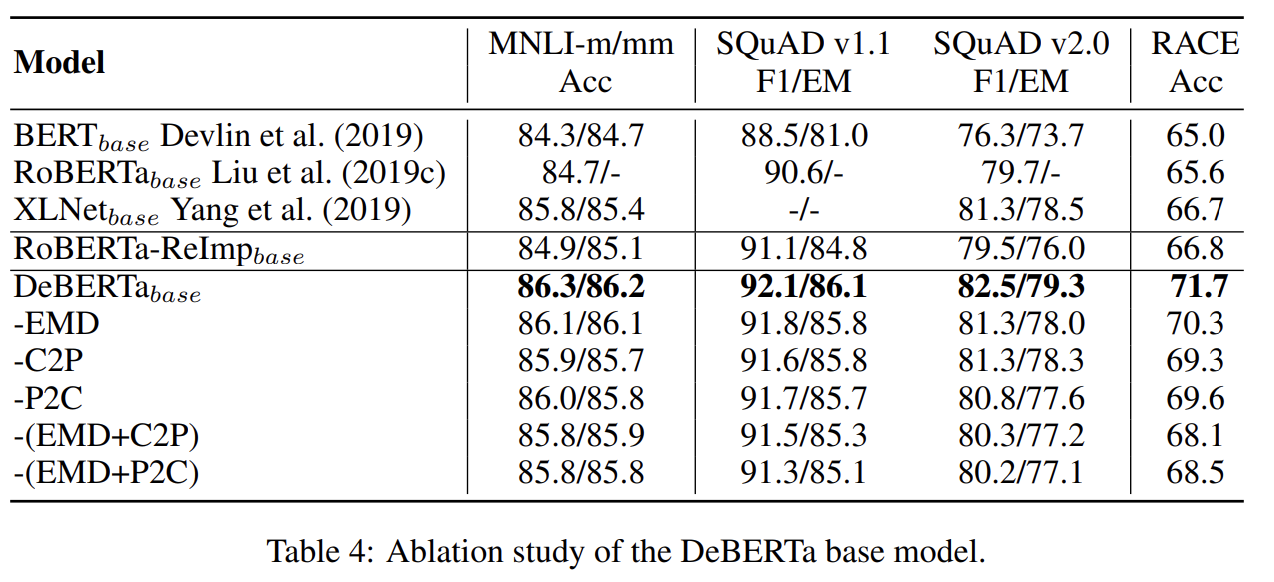
DeBERTa 각 구성요소의 효과를 알기 위해 ablation study도 한다. EMD를 뺀 것, 식 (4)의 content-to-position 항을 뺀 것, 식 (4)의 position-to-content 항을 뺀 것을 비교한다. (공평한 비교를 위해 실험 세팅대로 다시 학습시킨) RoBERTa-ReImp 모델이 RoBERTa와 모든 benchmark에서 비슷한 성능을 내어 실험 세팅이 합리적임을 알 수 있다. DeBERTa에서 어느 한 요소를 없애면 성능이 떨어졌고 두 개를 없애면 더 떨어졌다.
Strengths
- disentangled attention mechanism으로 content와 relative position을 따로 처리하고 enhanced mask decoder로 absolute position 정보를 보완한다. 위치 정보를 보완해 처리한 덕분에 성능이 향상된 것 같다.
- 새로운 virtual adversarial training algorithm인 Scale-invariant-Fine-Tuning (SiFT)를 도입해 모델을 일반화하는 regularization 효과를 얻었다.
개인적으로 Transformer 논문을 읽으면서 왜 positional encoding이랑 word embedding을 concatanate하는 것도 아니고 더하는지 이해가 안됐어서 이렇게 position과 content를 따로 처리하는 방법이 더 좋은 것 같다.