오늘의 리뷰는 그 유명한 GAN 논문이다.
아래 포스트들을 먼저 읽으면 도움이 될 것이다.
논문의 목표는 adversarial process를 통해 generative model을 추정하는 것이며, 이는 generative model G와 discriminative model D의 2가지로 이루어져 있다. G는 (input의) data distribution를 capture하고 D는 sample이 G로 만들어진 게 아니라 training data에서 온 것일 확률을 추정한다.
즉, G는 D가 구별하지 못하도록 random noise로부터 training set과 비슷한 데이터를 생성하고, D는 sample이 진짜 training set에서 왔는지 G가 만든건지 구분하려고 하는 것이다.
G가 training data distribution와 닮게 되면서 D가 실제 training 데이터인지 G가 생성한 가짜 데이터인지 판별하는 게 어려워져 확률은 1/2가 된다.
G, D는 모두 multi-layer perceptron으로 여기선 adversarial nets라고 부르며, 따라서 approximate inference나 Markov chains 필요 없이 backpropagation과 dropout algorithms으로 학습할 수 있다.
value function(=cost function)은 다음과 같다.
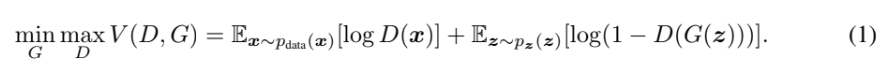
p_g는 G가 생성한 sample의 distribution, p_data는 input data의 distribution, p_z는 input noise의 distribution이다. D는 x가 p_g가 아닌 (input에서 왔을) 확률이다. D가 training example과 G가 생성한 sample 모두에 대해 올바른 label을 assign하도록 학습한다. 동시에 G가 log(1-D(G(z))를 최소화하도록 학습한다. 즉, G는 V를 minimize하게 학습하고 D는 maximize하게 학습한다. 이를 두고 D와 G가 two-player minimax game을 한다고 표현한다.
discriminator 관점에서 식 (1)의 각 항을 설명하자면, 첫 항은 data 분포를 따르는 x에 대해선 D가 1을 계산하게 하고, 둘째 항은 noise 분포를 따르는 z에 대해 G가 생성한 값이 D가 0으로 계산하게 하고 싶어하는 것이다.
반대로 generator 관점에서는 식 (1)의 두 번째 항에서 G(z)를 D가 1으로 판단하게 만들고자하는 것이다.
inner loop에서 D를 학습시키면 연산이 복잡하고 overfitting을 초래하기 때문에 D는 k step에 optimize하고 G는 1 step에 optimize한다. (D를 k단계마다 optimize하고 G를 1단계마다 optimize한다는 의미 같다.)
식 (1)은 G가 학습하기에 충분한 gradient를 제공 못 할 수 있다. 학습 초기에 G가 poor할 때 D는 G가 high confidence를 가진 sample조차도 training set과 명백히 달라서 reject할 수 있기 때문이다. 이 경우 log(1-D(G(z))가 saturate하므로 log(1-D(G(z))를 최소화하는 대신 log(D(G(z))를 최대화하게 G를 학습하는 게 좋다.

논문에서는 G, D의 이러한 min max game이 p_g=p_data에서 global optimum을 가진다는 것을 증명하고 위의 알고리즘 (1)이 식 (1)을 최적화한다는 것도 증명한다. 리뷰에선 그 증명을 생략하겠다. 궁금하다면 논문을 보거나 위의 포스트들을 보면 된다.
MNIST, Toronto Face Database(TFD), CIFAR-10 데이터셋을 이용해 학습했으며 Gaussian Parzen window density estimation으로 평가를 했다.

생성된 sample이 기존 모델들보다 더 좋다고는 할 수 없어도 adversarial model에 충분히 경쟁력이 있다는 점에서 의의를 두었다.
다른 framework에 비교했을 때 GAN에는 장단점이 있다. 우선 단점은 1. p_g(x)의 explicit reprensentation이 없다는 것과 2. training 중에 D가 반드시 G와 잘 synchronize되어야 한다는 점이다. computational한 장점은 1. Markov chain이 불필요하며 2. gradient를 얻기 위해 backprop만 있으면 되며 3. learning중 inference가 필요 없으며 4. model에 다양한 함수들이 포함될 수 있다는 것이다.
GAN의 statistical 장점은 1. generator network가 data exaple로부터 직접 update되지 않고, 즉 input component가 generator parameter에 직접 복사되지 않고, dircriminator를 통한 gradient의 흐름으로만 업데이트할 수 있다는 것과 2. sharp한, 심지어는 degenerate한 distribution까지도 표현할 수 있다는 것이다. 반면 Markov chains에 기반한 방법은 distribution이 blurry해야한다고 한다.
Strengths
- 증명을 통해 모델과 알고리즘의 이론적 기반을 견고히 했다.
- 논문에서 GAN의 장단점을 분석했다.
- 다양한 future works를 제시하여 발전 가능성과 방향을 제안했다.
adversarial이라는 아이디어가 신선하고 개념도 잘 이해가 됐지만 그와 별개로 논문 내용은 이해가 힘들었다. 나중에 코드로 실제로 구현해보고 싶다.