오늘 리뷰할 논문은 NiN 논문이다. 앞서 읽은 여러 논문에서 Lin et al.이란 이름으로 자주 등장하길래 도대체 무슨 논문인가 궁금해져서 읽게 되었다.
논문의 목표는 Network In Network(NIN)라고 이름붙인 deep network structure를 도입해 receptive field 내의 local patches의 model discriminability를 증가시키는 것이다.
아래 포스트를 먼저 읽으면 도움이 될 것이다.
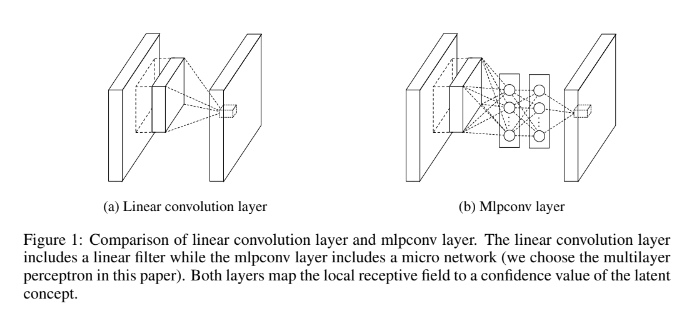
전통적인 convolutional layer은 input을 scan할 때 linear filter에 이은 nonlinear activation function을 사용한다. 그러나 여기선 receptive field 내의 data를 abstract하기 위해 더 복잡한 micro neural network 구조, 그러니까 multilayer perceptron(MLP)를 사용한다. 이 micro network가 (CNN처럼) input 위로 sliding하면서 feature map이 얻어진다. 이를 통해 local modeling이 향상되고, classification layer에선 (FC layer 대신) feature map에 global average pooling를 적용해서 전통적인 fully connected layer보다 이해하기 쉽고 overfitting에도 강하다.
abstraction을 통해 우리는 feature가 같은 개념의 다른 변형(variants)에 대해 invariant하길 바란다.
CNN 안의 convolution filter는 generalized linear model(GLM)이며, 저자들은 GLM을 가지고는 abstraction의 수준(level)이 낮다고 주장한다. GLM은 samples of the latent concepts가 linearly separable할 때 abstraction을 잘하기 때문이다. (그러나 input data는 종종 nonlinear하다.)
그래서 이들은 GLM을 더 potent nonlinear function approximator로 교체하는 것이 abstraction 능력을 향상시킬 것이라고 본다.
NIN에서 GLM은 general nonlinear function approximator인 micro network structure로 교체된다. 여기선 micro network의 instantiation으로써 MLP를 택하는데, 이는 MLP가 universal function approximator이면서 back-propagation으로 학습 가능하기 때문이다. 논문은 이 구조를 Figure (1)처럼 Mlpconv layer이라고 불렀다.
Mlpconv layer은 multiple fully connected layers와 nonlinear activation functions로 구성된 MLP를 통해 input local patch를 output feature vector로 mapping한다. 이때 MLP는 모든 local receptive field 사이에서 공유된다(CNN처럼 sliding하니까). 이렇게 Mlpconv layer를 stack한 전체 deep network를 NIN이라고 부른다.
또 classification에선 전통적인 fully connected layers 대신 마지막 mlpconv layer의 feature map을 spatial average해서 global average pooling layer를 통한 confidence of categories로 삼고, 그 결과(vector)를 softmax layer에 넣는다.
전통적인 CNN에선 (objective cost layer와 conv layer 사이의) fully connected layers가 black box처럼 작동하여 objective cost layer의 category level information이 어떻게 previous convolution layer로 다시 전해지는지 이해하기 어려웠다. 반면 global average pooling는 더 강력한 local modeling을 통해 feature maps와 categories간의 correspondance를 향상시켜 더 의미있고 interpretable하다. 또 fully connected layer는 overfitting에 취약하고 dropout regularization 지나치게 의존하지만, global
average pooling는 자연적으로 전체 구조에 대한 overfitting을 예방하여 그 자체로 structural regularizer가 된다.

앞서 말한 CNN/MLP의 단점을 좀 더 살펴보자. 식 (1)은 CNN의 feature map이 계산되는 것을 표현한 식이다. 이런 형태는 latent concept의 instance가 linearly separable할 때는 유리하지만, 좋은 abstraction은 일반적으로 highly nonlinear function이다. 전통적인 CNN은 over-complete set of filters를 사용해서 그런 nonlinear한 latent concept과 그 모든 변형을 감당하려한다.
이러면 각 linear filter가 같은 concept의 다른 variation을 탐지하도록 학습할 수 있지만, 같은 concept에 대해 너무 많은 filter를 부여하는 것은 다음 layer에 부담이 된다. 왜냐하면 그 층은 이전 층에 대한 모든 combinations of variation를 고려해야하기 때문이다.
또 CNN의 high layer은 original input의 큰 region에서 mapping되고(즉 receptive field가 크고), 이전 layer의 lower level concept를 조합해 higher level concept를 생성한다. 따라서 higher level concept로 combine하기 전에 저층에서 각 local patch에 더 좋은 abstraction을 하는 게 더 유익하다.
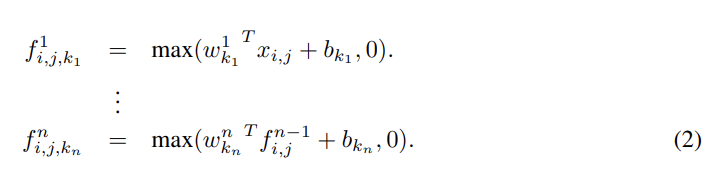
이제 MLP Convolution Layers에 대해 자세히 살펴보자. latent concept의 distribution에 대한 사전지식이 없을 때 local patch의 feature extraction에 universal function approximator를 사용하는 게 더 유리하다. latent concept에 대한 더 abstract representation이 근사 가능하기 때문이다. 논문은 universal function approximator 중에서 MLP를 선택했는데, 1. MLP가 back-propagation으로 학습하는 CNN 구조에 호환가능하기 때문이고 2. MLP가 feature re-use라는 정신(spirit)에 부합하는 deep model 그 자체가 될 수 있기 때문이다.
cross channel (cross feature map) pooling의 관점에서 식 (2)는 평범한 conv layer에서의 cascaded cross channel parametric pooling와 같다. 이 구조는 cross channel information의 복잡하고 learnable interaction을 가능하게 한다. 또 cross channel parametric pooling layer은 1x1 convolution kernel을 가진 convolution layer과도 동일하다.
maxout layer과 mlpconv layer를 비교하면, maxout layer은 convex function approximator인 한편 mlpconv layer은 universal function approximator라서 더 다양한 latent concept를 distribution을 modeling할 수 있다.
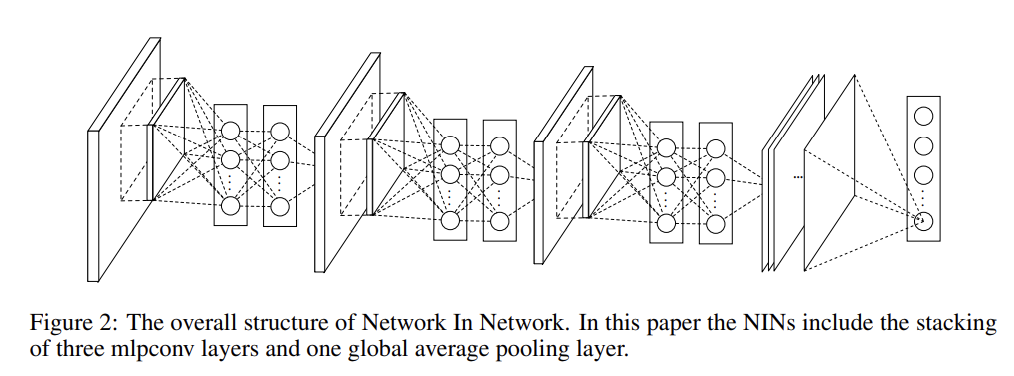
또 NIN이 classification에 사용하는 global average pooling에 대해서도 알아보자. 아이디어는 마지막 mlpconv layer에서 각 classification category에 대응하는 하나의 feature map을 생성하는 것이다. 각 feature map을 average낸 후 결과물 vector를 softmax layer(=objective cost layer)에 넣는다.
앞에서도 한 번 말했지만 다시 global average pooling의 장점을 설명하면 1. feature maps와 categories 사이의 향상된 correspondence 덕분에 feature maps을 categories confidence maps으로 간주할 수 있다는 것, 2. optimize할 parameter가 없기 때문에 overfitting을 피할 수 있다는 것, 3. global average pooling가 spatial information을 종합하기 때문에 input의 spatial translations에 더 robust하다는 것이다.
Strengths
- conv filter 대신 MLP를 이용해 feature abstract 능력을 향상시키려하는 시도가 특이했다. 덕분에 이 아이디어로부터 GoogLeNet 같은 여러 유명 논문이 비롯될 수 있었다.
- 마지막에 전통적인 FC layer 대신 global average pooling을 시도하여 confidence map으로 사용한 점이 독특했다.